山东省淄博市高三数学第二次高考模拟考试理 新人教版 17页

保密★启用前 高中三年级模拟考试 理科数学试题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共5页，满分150分，考试时间120分钟. 考试结束后，将本试卷和答题卡一并交回.‎ 注意事项：‎ ‎1. 答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上，并将准考证号条形码粘贴在答题卡上指定位置.‎ ‎2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上.‎ ‎3. 第Ⅱ卷必须用0.5毫米黑色签字笔在答题卡各题的答题区域内作答；不能写在试题卷上； 如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸，修正带，不按以上要求作答的答案无效.‎ ‎4. 填空题请直接填写答案，解答题应写出文字说明，证明过程或演算步骤.‎ 参考公式：‎ 锥体的体积公式：V=，其中S是锥体的底面积，h是锥体的高.‎ ‎ 如果事件互斥，那么 ‎ 如果事件相互独立，那么 ‎ 第Ⅰ卷(选择题 共60分)‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 若复数z满足 则z对应的点位于 ‎ ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2. 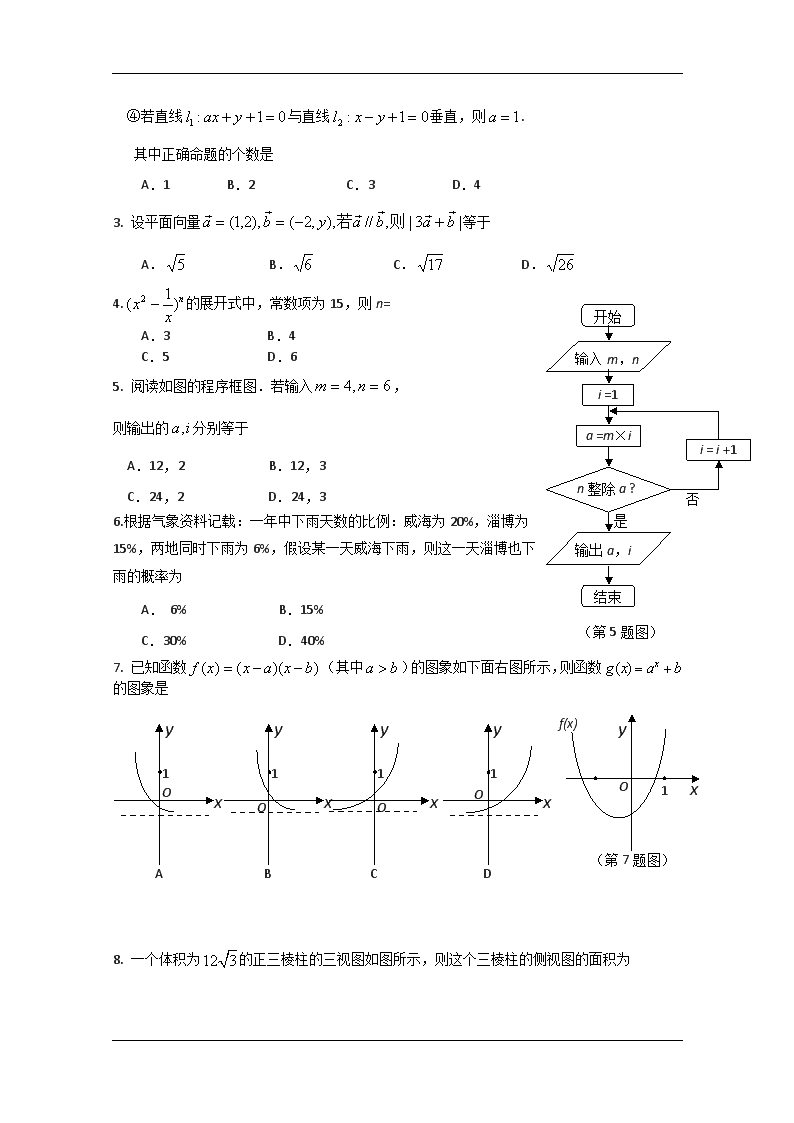给出下列四个命题: ‎ ‎①若集合满足 则； ‎ ‎②给定命题， 若“”为真，则“”为真；‎ ‎③设，若则；‎ ‎④若直线与直线垂直，则.‎ 其中正确命题的个数是 ‎ A．1 B．2 C．3 D．4‎ ‎3. 设平面向量等于 ‎ A． B． C． D．‎ 开始 输出a，i i =1‎ a =m×i n整除a ?‎ 输入m，n 结束 i = i +1‎ 是 否 ‎（第5题图）‎ ‎4.的展开式中，常数项为15，则n= ‎ ‎ A．3 B．4 ‎ C．5 D．6‎ ‎5. 阅读如图的程序框图．若输入，‎ 则输出的分别等于 ‎ ‎ A．12，2 B．12，3 ‎ ‎ C．24，2 D．24，3‎ ‎6.根据气象资料记载：一年中下雨天数的比例：威海为20%，淄博为15%，两地同时下雨为6%，假设某一天威海下雨，则这一天淄博也下雨的概率为 A． 6% B．15% ‎ ‎ C．30% D．40%‎ ‎（第7题图）‎ ‎1‎ x y o f(x)‎ ‎1‎ o x y A ‎1‎ o x y B ‎1‎ o x y C ‎1‎ o x y D ‎7. 已知函数（其中）的图象如下面右图所示，则函数的图象是 ‎ ‎8. 一个体积为的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为 ‎ 侧视图 正视图 俯视图 ‎（第8题图）‎ A． B．8 C． D．12 ‎ ‎9．不等式对任意实数恒成立，则实数的取值范围为 A． B． C． D．‎ ‎10．已知函数的反函数为，且有，若，，则的最小值为 ‎ ‎ A． B． C． D． ‎ ‎11．直线与圆相交于A、B两点（其中是实数），且是直角三角形(O是坐标原点)，则点P与点之间距离的最小值为 A B. C. D. ‎ ‎12.已知关于的方程的两根分别为、，且，则的取值范围是 A． B． C． D．‎ 第Ⅱ卷(非选择题 共90分)‎ 二、填空题：本大题共4小题，每小题4分，共16分.（注意：在试题卷上作答无效）‎ ‎13． . ‎ ‎14．数列满足，若，则的值为 . ‎ ‎15．设奇函数在（0，+∞）上为增函数，且，则不等式的解集是 ．‎ ‎16．过双曲线的一个焦点F作一条渐近线的垂线，若垂足恰在线段OF（O为原点）的垂直平分线上，则双曲线的离心率为 ．‎ 三、解答题：本大题共6小题，共74分.（注意：在试题卷上作答无效）‎ ‎17.(本小题满分12分)‎ 已知，，其中，‎ 若函数，且函数的图象与直线相邻两公共点间的距离为.‎ ‎ （Ⅰ）求的值；‎ ‎ （Ⅱ）在中，a、b、c分别是角A、B、C、的对边，且， ，求的面积.‎ ‎18. (本小题满分12分) ‎ 为了让更多的人参与2010年在上海举办的“世博会”，上海某旅游公司面向国内外发行一定数量的旅游优惠卡，其中向境外人士发行的是世博金卡（简称金卡），向境内人士发行的是世博银卡（简称银卡）.现有一个由36名游客组成的旅游团到上海参观旅游，其中27名境外游客，其余是境内游客.在境外游客中有持金卡，在境内游客中有持银卡..‎ ‎（Ⅰ）在该团中随机采访3名游客，求恰有1人持金卡，至多1人持银卡的概率；‎ ‎（Ⅱ）在该团的境内游客中随机采访3名游客，设其中持银卡人数为随机变量，‎ 求的分布列及数学期望. ‎ ‎19. (本小题满分12分)‎ C1‎ B1‎ A1‎ B A D C ‎（第19题图）‎ 如图，在直三棱柱中，.‎ ‎（Ⅰ）若为中点，求证：平面平面；‎ ‎（Ⅱ）在上是否存在一点，使得二面角的大小为60°. ‎ ‎20.（本小题满分12分） ‎ 已知二次函数有且只有一个零点，数列的前项和.‎ ‎ （Ⅰ）求数列的通项公式；‎ ‎ （Ⅱ）设，定义所有满足的正整数m的个数，称为这个数列的变号数，求数列的变号数.‎ ‎21. (本小题满分12分)‎ 已知直线与函数的图象相切于点，且与函数 的图象也相切.‎ ‎ （Ⅰ）求直线的方程及的值；‎ ‎（Ⅱ）若（其中是的导函数），求函数的最大值；‎ ‎（Ⅲ）当时，求证：.‎ ‎22.(本小题满分14分)(理科)‎ 如图，已知直线过椭圆的右焦点，抛物线：的焦点为椭圆的上顶点，且直线交椭圆于、两点，点、、 在直线上的射影依次为点、、.‎ ‎ （Ⅰ）求椭圆的方程；‎ ‎ （Ⅱ）若直线l交y轴于点，且，当变化时，探求 的值是否为定值？若是，求出的值，否则，说明理由；‎ ‎ （Ⅲ）连接、，试探索当变化时，直线与是否相交于定点？‎ 若是，请求出定点的坐标，并给予证明；否则，说明理由.‎ 保密★启用前 高中三年级模拟考试 理科数学参考答案及评分标准 第Ⅰ卷(选择题 共60分)‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 若复数z满足 则z对应的点位于 ‎ ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2. 给出下列四个命题: ‎ ‎①若集合满足 则； ‎ ‎②给定命题, 若“”为真，则“”为真；‎ ‎③设 若则；‎ ‎④若直线与直线垂直，则.‎ 其中正确命题的个数是 ‎ A．1 B．2 C．3 D．4‎ 开始 输出a，i i =1‎ a =m×i n整除a ?‎ 输入m，n 结束 i = i +1‎ 是 否 ‎（第5题图）‎ ‎3. 设平面向量等于 ‎ A． B． C． D．‎ ‎4. 的展开式中，常数项为15，则n= ‎ ‎ A．3 B．4 ‎ C．5 D．6‎ ‎5. 阅读如图的程序框图．若输入，‎ 则输出的分别等于 ‎ ‎ A．12，2 B．12，3 ‎ ‎ C．24，2 D．24，3‎ ‎6. 根据气象资料记载：一年中下雨天数的比例：威海为20%，淄博为15%，两地同时下雨为6%，假设某一天威海下雨，则这一天淄博也下雨的概率为 A． 6% B．15% ‎ ‎ C．30% D．40%‎ ‎（第7题图）‎ ‎1‎ x y o f(x)‎ ‎1‎ o x y A ‎1‎ o x y B ‎1‎ o x y C ‎1‎ o x y D ‎7. 已知函数（其中）的图象如下面右图所示，则函数的图象是 ‎ 侧视图 正视图 俯视图 ‎（第8题图）‎ ‎8. 一个体积为的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为 ‎ A． B．8 C． D．12 ‎ ‎9．不等式对任意实数恒成立，则实数的取值范围为 A． B． ‎ C． D．‎ ‎10．已知函数的反函数为，且有，若,，则的最小值为 ‎ ‎ A． B． C． D． ‎ ‎11．直线与圆相交于A、B两点（其中是实数），且是直角三角形(O是坐标原点)，则点P与点之间距离的最小值为 A B. C. D. ‎ ‎12．已知关于的方程的两根分别为、，且，则的取值范围是 A． B． C． D．‎ 第Ⅱ卷(非选择题 共90分)‎ 二、填空题：本大题共4小题，每小题4分，共16分.（注意：在试题卷上作答无效）‎ ‎13．； ‎ ‎14．数列满足，若，则的值为 ‎15．设奇函数在（0，+∞）上为增函数，且，则不等式的解集是 ．‎ ‎16．过双曲线的一个焦点F作一条渐近线的垂线，若垂足恰在线段OF（O为原点）的垂直平分线上，则双曲线的离心率为．‎ 三、解答题：本大题共6小题，共74分.（注意：在试题卷上作答无效）‎ ‎17.(本小题满分12分)‎ 已知，，其中，‎ 若函数，且函数的图象与直线相邻两公共点间的距离为.‎ ‎ （Ⅰ）求的值；‎ ‎ （Ⅱ）在中，a、b、c分别是角A、B、C、的对边，且， ，求的面积.‎ 解：（Ⅰ）‎ ‎……………………………………………… 3分 ‎ 函数的周期 函数的图象与直线相邻两公共点间的距离为.‎ ‎ …………………………………………………………… 6分 ‎（Ⅱ）由（Ⅰ）可知，‎ ‎ ‎ ‎ ‎ ‎……………………………………………………………8分 由余弦定理知 ‎ 又 ‎ 联立解得或……………………………………………… 10分 ‎ …………………………………………………… 12分 ‎ （或用配方法， ‎ ‎）‎ ‎18. (本小题满分12分) ‎ 为了让更多的人参与2010年在上海举办的“世博会”，上海某旅游公司面向国内外发行一定数量的旅游优惠卡，其中向境外人士发行的是世博金卡（简称金卡），向境内人士发行的是世博银卡（简称银卡）.现有一个由36名游客组成的旅游团到上海参观旅游，其中27名境外游客，其余是境内游客.在境外游客中有持金卡，在境内游客中有持银卡..‎ ‎（I）在该团中随机采访3名游客，求恰有1人持金卡，至多1人持银卡的概率；‎ ‎（Ⅱ）在该团的境内游客中随机采访3名游客，设其中持银卡人数为随机变量，‎ 求的分布列及数学期望.‎ 解：（I）由题意得，境外游客中有9人持金卡；境内游客共有9人，其中6人持银卡；旅游团中共有21人不持卡. ……………………1分 设“所采访的3人中，恰有1人持金卡，至多1人持银卡”为事件，“所采访的3人中，恰有1人持金卡，0人持银卡”为事件，“所采访的3人中，恰有1人持金卡，1人持银卡”为事件.‎ ‎ 则 ………………………4分 ‎ ‎ ‎ ∴ 在该团中随机采访3人，恰有1人持金卡，至多1人持银卡的概率是 ‎…………………………………………………………6分 ‎（Ⅱ）的可能取值为0，1，2，3‎ ‎ , . ‎ ‎ ， （每个1分） ………………10分 ‎ 的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎ …………………………………………………………11分 C1‎ B1‎ A1‎ B A D C ‎（第19题图）‎ ‎∴ . ………………………………12分 ‎ ‎19. (本小题满分12分) ‎ 如图，在直三棱柱中，.‎ ‎（Ⅰ）若为中点，求证：平面平面；‎ ‎（Ⅱ）在上是否存在一点，使得二面角 的大小为60°. ‎ 解法一：（Ⅰ）证明：∵‎ ‎∴‎ 又由直三棱柱性质知 ………………1分∴平面.‎ ‎∴ ………………2分 由，为中点，可知，‎ ‎∴即 ………………4分 又 ∴ 平面 ‎ 又平面 故平面平面 ……………………………6分 ‎ B A C D A1‎ E B1‎ C1‎ ‎（第19题图）‎ ‎（Ⅱ）解：当时二面角的大小为60°. ……………7分 假设在上存在一点满足题意，‎ 由（Ⅰ）可知平面.如图，在平面内过作，交或延长线或于，连，则 所以为二面角的平面角 ………………8分 ‎∴‎ 由知， ………………………10分 设 ，则 ‎∵的面积为1 ∴‎ x C1‎ B1‎ A1‎ B A D C z y ‎（第19题图）‎ 解得，即 ‎ ‎∴在上存在一点满足题意……………………12分 解法二：‎ ‎（Ⅰ）如图，以为原点，所在直线为 轴建立空间直角坐标系. ‎ 则.‎ 即 ……2分 由得 由得 ………………4分 又 ‎∴平面 又平面 ‎∴平面平面 ………………………………6分 ‎（Ⅱ）当时二面角的大小为60°. ……………7分 设，则点坐标为，‎ 设平面的法向量为 ‎ 则由 令 得 …………8分 又∵为平面的法向量 则由 …………10分 解得，故. ‎ ‎∴在上存在一点满足题意………………………………12分 ‎20.（本小题满分12分） ‎ 已知二次函数有且只有一个零点，数列的前项和.‎ ‎ （Ⅰ）求数列的通项公式；‎ ‎ （Ⅱ）设，定义所有满足的正整数m的个数，称为这个数列的变号数，求数列的变号数.‎ 解：（Ⅰ）依题意，　　‎ ‎　　又由得 ‎　　‎ ‎　　当时，；‎ ‎　　当时，‎ ‎　　…………………………………6分 ‎ （Ⅱ）由题设 由可知，当时，恒有……………8分 又，，，‎ 即，，‎ 所以，数列共有三个变号数，即变号数为3. …………………………12分 ‎21. (本小题满分12分)‎ 已知直线与函数的图象相切于点，且与函数 的图象也相切.‎ ‎ （Ⅰ）求直线的方程及的值；‎ ‎（Ⅱ）若（其中是的导函数），求函数的最大值；‎ ‎（Ⅲ）当时，求证：.‎ 解：（Ⅰ）∵，直线是函数的图象在点处的切线，‎ ‎ ∴其斜率为 ‎ ∴直线的方程为． ……………2分 ‎ 又因为直线与的图象相切 ‎∴ ，‎ ‎ 得（不合题意，舍去） ……………4分 ‎ （Ⅱ）由（Ⅰ）知，‎ ‎∴（），‎ ‎∴．（） ……………6分 当时，；当时，．‎ 于是，在上单调递增，在上单调递减． ……………8分 所以，当时，取得最大值； ……………9分 ‎（Ⅲ）由（Ⅱ）知：当时，，即，…………10分 当时， ‎ ‎∴． ……………12分， ‎ ‎22.(本小题满分14分)‎ 如图，已知直线过椭圆的右焦点，抛物线：的焦点为椭圆的上顶点，且直线交椭圆于、两点，点、、 在直线上的射影依次为点、、.‎ ‎ （Ⅰ）求椭圆的方程；‎ ‎ （Ⅱ）若直线l交y轴于点，且，当变化时，探求 的值是否为定值？若是，求出的值，否则，说明理由；‎ ‎ （Ⅲ）连接、，试探索当变化时，直线与是否相交于定点？‎ 若是，请求出定点的坐标，并给予证明；否则，说明理由.‎ 解：（Ⅰ）易知椭圆右焦点∴，‎ 抛物线的焦点坐标 ‎ 椭圆的方程……………3分 ‎ （Ⅱ）易知，且与轴交于，‎ 设直线交椭圆于 由 ‎ ‎∴‎ ‎∴……………6分 ‎ 又由 ‎ ‎ ‎ 同理 ‎ ∴‎ ‎∵ ‎ ‎∴……………9分 所以，当变化时， 的值为定值；……………10分 ‎（Ⅲ）先探索，当时，直线轴，则为矩形，由对称性知，与相交的中点，且，‎ 猜想：当变化时，与相交于定点……………11分 证明：由（Ⅱ）知，∴‎ ‎ 当变化时，首先证直线过定点，‎ 方法1）∵‎ 当时，‎ ‎∴点在直线上，‎ 同理可证，点也在直线上；‎ ‎∴当变化时，与相交于定点……………14分 方法2）∵‎ ‎ ‎ ‎ ∴‎ ‎∴、、三点共线，‎ ‎ 同理可得、、也三点共线；‎ ‎ ∴当变化时，与相交于定点……………14分