备考20142013高考数学 真题模拟新题分类汇编 立体几何 文 47页

立体几何 ‎ G1　空间几何体的结构　　　　　　　　　　　　　　　　　　　‎ ‎8．G1，G6[2013·北京卷] 如图1－2，在正方体ABCD－A1B‎1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有(　　)‎ 图1－2‎ A．3个 B．4个 C．5个 D．6个 ‎8．B　[解析] 设棱长为1，∵BD1＝，∴BP＝，D1P＝.联结AD1，B1D1，CD1，得△ABD1≌△CBD1≌△B1BD1，‎ ‎∴∠ABD1＝∠CBD1＝∠B1BD1，且cos∠ABD1＝，‎ 联结AP，PC，PB1，则有△ABP≌△CBP≌△B1BP，‎ ‎∴AP＝CP＝B1P＝，同理DP＝A1P＝C1P＝1，‎ ‎∴P到各顶点的距离的不同取值有4个．‎ ‎18．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC中，D，E分别是AB，AC上的点，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图1－4(2)所示的三棱锥A－BCF，其中BC＝.‎ 图1－4‎ ‎(1)证明：DE∥平面BCF；‎ ‎(2)证明：CF⊥平面ABF；‎ ‎(3)当AD＝时，求三棱锥F－DEG的体积．‎ ‎18．解：‎ G2　空间几何体的三视图和直观图　　　　　　　　　　　　　　　　　　　‎ ‎10．G2，G7[2013·北京卷] 某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．‎ 图1－3‎ ‎10．3　[解析] 正视图的长为3，侧视图的长为3，因此，该四棱锥底面是边长为3的正方形，且高为1，因此V＝×(3×3)×1＝3.‎ ‎18．G2，G4[2013·福建卷] 如图1－3，在四棱锥P－ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，BC＝5，DC＝3，AD＝4，∠PAD＝60°.‎ ‎(1)当正视方向与向量的方向相同时，画出四棱锥P－ABCD的正视图(要求标出尺寸，并写出演算过程)；‎ ‎(2)若M为PA的中点，求证：DM∥平面PBC；‎ ‎(3)求三棱锥D－PBC的体积．‎ 图1－3‎ ‎18．解：(1)在梯形ABCD中，过点C作CE⊥AB，垂足为E.‎ 由已知得，四边形ADCE为矩形，AE＝CD＝3，‎ 在Rt△BEC中，由BC＝5，CE＝4，依勾股定理得BE＝3，从而AB＝6.‎ 又由PD⊥平面ABCD得，PD⊥AD.‎ 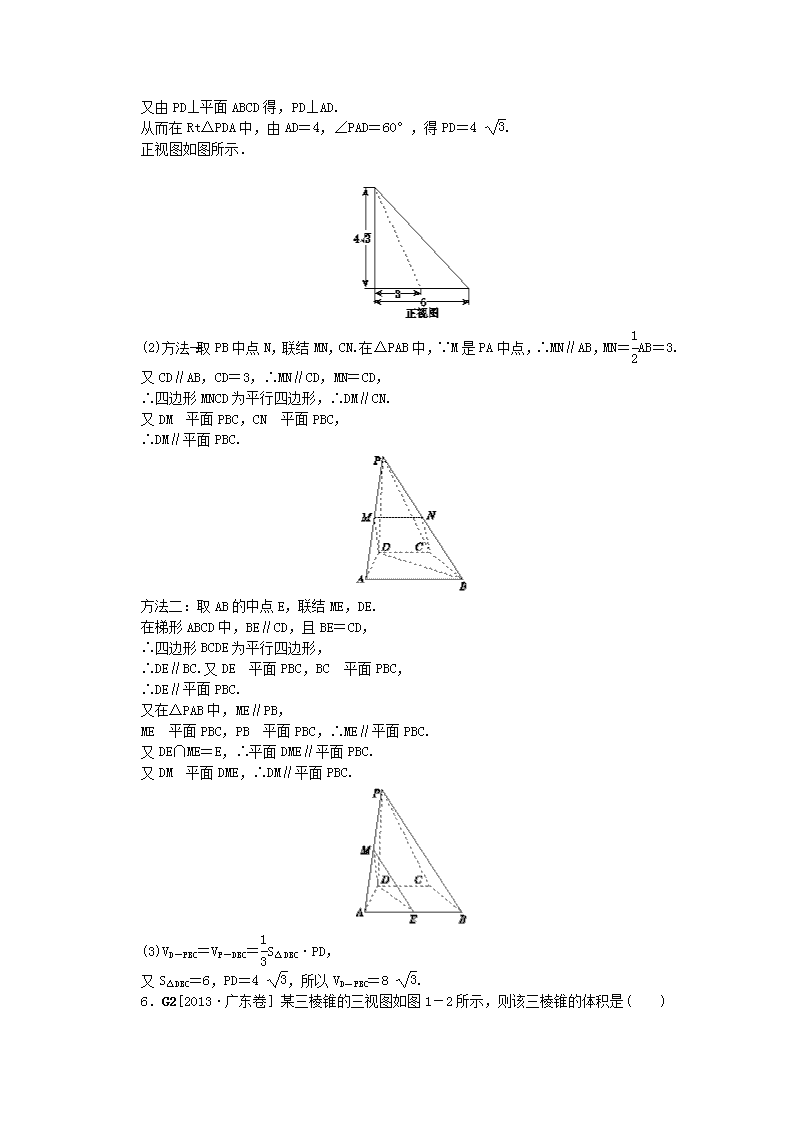从而在Rt△PDA中，由AD＝4，∠PAD＝60°，得PD＝4 .‎ 正视图如图所示．‎ ‎(2)方法一：取PB中点N，联结MN，CN.在△PAB中，∵M是PA中点，∴MN∥AB，MN＝AB＝3.‎ 又CD∥AB，CD＝3，∴MN∥CD，MN＝CD，‎ ‎∴四边形MNCD为平行四边形，∴DM∥CN.‎ 又DM平面PBC，CN平面PBC，‎ ‎∴DM∥平面PBC.‎ 方法二：取AB的中点E，联结ME，DE.‎ 在梯形ABCD中，BE∥CD，且BE＝CD，‎ ‎∴四边形BCDE为平行四边形，‎ ‎∴DE∥BC.又DE平面PBC，BC平面PBC，‎ ‎∴DE∥平面PBC.‎ 又在△PAB中，ME∥PB，‎ ME平面PBC，PB平面PBC，∴ME∥平面PBC.‎ 又DE∩ME＝E，∴平面DME∥平面PBC.‎ 又DM平面DME，∴DM∥平面PBC.‎ ‎(3)VD－PBC＝VP－DBC＝S△DBC·PD，‎ 又S△DBC＝6，PD＝4 ，所以VD－PBC＝8 .‎ ‎6．G2[2013·广东卷] 某三棱锥的三视图如图1－2所示，则该三棱锥的体积是(　　)‎ 图1－2‎ A. B. ‎ C. D．1‎ ‎6．B　[解析] 由三视图得三棱锥的高是2，底面是一个腰为1的等腰直角三角形，故体积是××1×1×2＝，选B.‎ ‎5．G2[2013·广东卷] 执行如图1－1所示的程序框图，若输入n的值为3，则输出s的值是(　　)‎ 图1－1‎ A．1 B．2 ‎ C．4 D．7 ‎ ‎5．C　[解析] 1≤3，s＝1＋0＝1，i＝2；2≤3，s＝1＋1＝2，i＝3；s＝2＋2＝4，i＝4；4>3，故输出s＝4，选C.‎ ‎7．G2[2013·湖南卷] 已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为的矩形，则该正方体的正视图的面积等于(　　)‎ A. B．1‎ C. D. ‎7．D　[解析] 由题可知，其俯视图恰好是正方形，而侧视图和正视图则应该都是正方体的对角面，故面积为，选D.‎ ‎8．G2[2013·江西卷] 一几何体的三视图如图1－2所示，则该几何体的体积为(　　)‎ 图1－2‎ A．200＋9π B．200＋18π C．140＋9π D．140＋18π ‎8．A　[解析] 该几何体上面是半圆柱，下面是长方体，半圆柱体积为π·32·2＝9π，长方体体积为10×5×4＝200.故选A.‎ ‎13．G2[2013·辽宁卷] 某几何体的三视图如图1－3所示，则该几何体的体积是________．‎ 图1－3‎ ‎13．16π－16　[解析] 由三视图可知该几何体是一个圆柱里面挖去了一个长方体，所以该几何体的体积为V＝4π×4－16＝16π－16.‎ ‎9．G2[2013·新课标全国卷Ⅱ] 一个四面体的顶点在空间直角坐标系O－xyz中的坐标分别是(1，0，1)，(1，1，0)，(0，1，1)，(0，0，0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为(　　)‎ 图1－3‎ ‎9．A　[解析] 在空间直角坐标系O－xyz中画出三棱锥，由已知可知三棱锥O－ABC为题中所描叙的四面体，而其在zOx平面上的投影为正方形EBDO，故选A.‎ 图1－4‎ ‎4．G2[2013·山东卷]‎ ‎ 一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图1－1所示，则该四棱锥侧面积和体积分别是(　　)‎ 图1－1‎ A．4 ，8 B．4 ， C．4(＋1)， D．8，8‎ ‎4．B　[解析] 由正视图知该几何体的高为2，底面边长为2，斜高为＝，∴侧面积＝4××2×＝4 ，体积为×2×2×2＝.‎ ‎12．G2[2013·陕西卷] 某几何体的三视图如图1－2所示，则其表面积为________．‎ 图1－2‎ ‎12．3π　[解析] 由三视图得该几何体为半径为1的半个球，则表面积为半球面＋底面圆，代入数据计算为S＝×4π×12＋π×12＝3π.‎ ‎11．G2[2013·新课标全国卷Ⅰ] 某几何体的三视图如图1－3所示，则该几何体的体积为(　　)‎ 图1－3‎ A．16＋8π B．8＋8π C．16＋16π D．8＋16π ‎11．A　[解析] 该空间几何体的下半部分是一个底面半径为2，母线长为4的半圆柱，上半部分是一个底面边长为2、高为4的正四棱柱．这个空间几何体的体积是×π×4×4＋2×2×4＝16＋8π.‎ ‎5．G2[2013·浙江卷] 已知某几何体的三视图(单位： cm)如图1－1所示，则该几何体的体积是(　　)‎ 图1－1‎ A．‎108 cm3 B．‎100 cm3‎ C．‎92 cm3 D．‎84 cm3‎ ‎5．B　[解析] 此直观图是由一个长方体挖去一个三棱锥而得，如图所示其体积为3×6×6－××3×4×4＝108－8＝100(cm3)．所以选择B.‎ ‎19．G2和G5[2013·重庆卷] 如图1－4所示，四棱锥P－ABCD中，PA⊥底面ABCD，PA＝2 ，BC＝CD＝2，∠ACB＝∠ACD＝.‎ ‎(1)求证：BD⊥平面PAC；‎ ‎(2)若侧棱PC上的点F满足PF＝7FC，求三棱锥P－BDF的体积．‎ 图1－4‎ ‎19．解：(1)证明：因为BC＝CD，即△BCD为等腰三角形，又∠ACB＝∠ACD，故BD⊥AC.‎ 因为PA⊥底面ABCD，所以PA⊥BD，从而BD与平面PAC内两条相交直线PA，AC都垂直，所以BD⊥平面PAC.‎ ‎(2)三棱锥P－BCD的底面BCD的面积S△BCD＝BC·CD·sin∠BCD＝·2·2·sin＝.‎ 由PA⊥底面ABCD，得 VP－BCD＝·S△BCD·PA＝××2 ＝2.‎ 由PF＝7FC，得三棱锥F－BCD的高为PA，故VF－BCD＝·S△BCD·PA＝×××2 ＝，‎ 所以VP－BDF＝VP－BCD－VF－BCD＝2－＝.‎ ‎8．G2和G7[2013·重庆卷] 某几何体的三视图如图1－3所示，则该几何体的表面积为(　　)‎ 图1－3‎ A．180 B．‎200 C．220 D．240‎ ‎8．D　[解析] 该几何体为直四棱柱，其高为10，底面是上底为2，下底为8，高为4，其腰为5的等腰梯形，所以底面面积和为(2＋8)×4×2＝40.四个侧面的面积和为(2＋8＋5×2)×10＝200，所以该直四棱柱的表面积为S＝40＋200＝240，故选D.‎ G3　平面的基本性质、空间两条直线　　　　　　　　　　　　　　　　　　　‎ G4　空间中的平行关系　　　　　　　　　　　　　　　　　　　‎ ‎17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：‎ ‎(1)PA⊥底面ABCD；‎ ‎(2)BE∥平面PAD；‎ ‎(3)平面BEF⊥平面PCD.‎ 图1－5‎ ‎17．证明：(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD.‎ ‎(2)因为AB∥CD，CD＝2AB，E为CD的中点，‎ 所以AB∥DE，且AB＝DE，‎ 所以ABED为平行四边形，‎ 所以BE∥AD.‎ 又因为BE平面PAD，AD平面PAD，‎ 所以BE∥平面PAD.‎ ‎(3)因为AB⊥AD，而且ABED为平行四边形，‎ 所以BE⊥CD，AD⊥CD.‎ 由(1)知PA⊥底面ABCD，‎ 所以PA⊥CD.‎ 又因为AD∩PA＝A，所以CD⊥平面PAD，‎ 所以CD⊥PD.‎ 因为E和F分别是CD和PC的中点，‎ 所以PD∥EF，‎ 所以CD⊥EF，‎ 所以CD⊥平面BEF，‎ 所以平面BEF⊥平面PCD.‎ ‎18．G2，G4[2013·福建卷] 如图1－3，在四棱锥P－ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，BC＝5，DC＝3，AD＝4，∠PAD＝60°.‎ ‎(1)当正视方向与向量的方向相同时，画出四棱锥P－ABCD的正视图(要求标出尺寸，并写出演算过程)；‎ ‎(2)若M为PA的中点，求证：DM∥平面PBC；‎ ‎(3)求三棱锥D－PBC的体积．‎ 图1－3‎ ‎18．解：(1)在梯形ABCD中，过点C作CE⊥AB，垂足为E.‎ 由已知得，四边形ADCE为矩形，AE＝CD＝3，‎ 在Rt△BEC中，由BC＝5，CE＝4，依勾股定理得BE＝3，从而AB＝6.‎ 又由PD⊥平面ABCD得，PD⊥AD.‎ 从而在Rt△PDA中，由AD＝4，∠PAD＝60°，得PD＝4 .‎ 正视图如图所示．‎ ‎(2)方法一：取PB中点N，联结MN，CN.在△PAB中，∵M是PA中点，∴MN∥AB，MN＝AB＝3.‎ 又CD∥AB，CD＝3，∴MN∥CD，MN＝CD，‎ ‎∴四边形MNCD为平行四边形，∴DM∥CN.‎ 又DM平面PBC，CN平面PBC，‎ ‎∴DM∥平面PBC.‎ 方法二：取AB的中点E，联结ME，DE.‎ 在梯形ABCD中，BE∥CD，且BE＝CD，‎ ‎∴四边形BCDE为平行四边形，‎ ‎∴DE∥BC.又DE平面PBC，BC平面PBC，‎ ‎∴DE∥平面PBC.‎ 又在△PAB中，ME∥PB，‎ ME平面PBC，PB平面PBC，∴ME∥平面PBC.‎ 又DE∩ME＝E，∴平面DME∥平面PBC.‎ 又DM平面DME，∴DM∥平面PBC.‎ ‎(3)VD－PBC＝VP－DBC＝S△DBC·PD，‎ 又S△DBC＝6，PD＝4 ，所以VD－PBC＝8 .‎ ‎18．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC中，D，E分别是AB，AC上的点，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图 ‎1－4(2)所示的三棱锥A－BCF，其中BC＝.‎ 图1－4‎ ‎(1)证明：DE∥平面BCF；‎ ‎(2)证明：CF⊥平面ABF；‎ ‎(3)当AD＝时，求三棱锥F－DEG的体积．‎ ‎18．解：‎ ‎8．G4、G5[2013·广东卷] 设l为直线，α，β是两个不同的平面，下列命题中正确的是(　　)‎ A．若l∥α，l∥β，则α∥β B．若l⊥α，l⊥β，则α∥β C．若l⊥α，l∥β，则α∥β D．若α⊥β，l∥α，则l⊥β ‎8．B　[解析] 根据空间平行、垂直关系的判定和性质，易知选B.‎ ‎16．G4，G5[2013·江苏卷] 如图1－2，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．‎ 求证：(1)平面EFG∥平面ABC；‎ ‎(2)BC⊥SA.‎ 图1－2‎ ‎16．证明：(1)因为AS＝AB，AF⊥SB，垂足为F，所以F是SB的中点．又因为E是SA的中点，所以EF∥AB.‎ 因为EF平面ABC，AB平面ABC，‎ 所以EF∥平面ABC.‎ 同理EG∥平面ABC.又EF∩EG＝E，‎ 所以平面EFG∥平面ABC.‎ ‎(2)因为平面SAB⊥平面SBC，且交线为SB，‎ 又AF平面SAB，AF⊥SB，‎ 所以AF⊥平面SBC.‎ 因为BC平面SBC，所以AF⊥BC.‎ 又因为AB⊥BC，AF∩AB＝A，AF，AB平面SAB，所以BC⊥平面SAB.‎ 因为SA平面SAB，所以BC⊥SA.‎ ‎15．G4[2013·江西卷] 如图1－5所示，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，则直线EF与正方体的六个面所在的平面相交的平面个数为________．‎ 图1－5‎ ‎15．4　[解析] 直线EF与正方体左右两个面平行，与其他四个面相交．‎ 图1－4‎ ‎18．G4，G5[2013·辽宁卷] 如图1－4，AB是圆O的直径，PA垂直圆O所在的平面，C是圆O上的点．‎ ‎(1)求证：BC⊥平面PAC；‎ ‎(2)设Q为PA的中点，G为△AOC的重心，求证：QG∥平面PBC.‎ ‎18．证明：(1)由AB是圆O的直径，得AC⊥BC.‎ 由PA⊥平面ABC，BC平面ABC，得PA⊥BC.‎ 又PA∩AC＝A，PA平面PAC，AC平面PAC，‎ 所以BC⊥平面PAC.‎ ‎(2)联结OG并延长交AC于M，联结QM，QO，‎ 由G为△AOC的重心，得M为AC中点，‎ 由Q为PA中点，得QM∥PC.‎ 又O为AB中点，得OM∥BC.‎ 因为QM∩MO＝M，QM平面QMO.‎ MO平面QMO，‎ BC∩PC＝C，BC平面PBC，PC平面PBC，‎ 所以平面QMO∥平面PBC.‎ 因为QG平面QMO，‎ 所以QG∥平面PBC.‎ ‎18．G4，G7，G11[2013·新课标全国卷Ⅱ] 如图，直三棱柱ABC－A1B‎1C1中，D，E分别是AB，BB1的中点．‎ ‎(1)证明：BC1∥平面A1CD；‎ ‎(2)设AA1＝AC＝CB＝2，AB＝2，求三棱锥C－A1DE的体积．‎ 图1－7‎ ‎18．解：(1)证明：联结AC1交A‎1C于点F，则F为AC1中点．又D是AB中点，联结DF，则BC1∥DF.因为DF平面A1CD，BC1平面A1CD，所以BC1∥平面A1CD.‎ 图1－8‎ ‎(2)因为ABC－A1B‎1C1是直三棱柱，所以AA1⊥CD.由已知AC＝CB，D为AB的中点，所以CD⊥AB.又AA1∩AB＝A，于是CD⊥平面ABB‎1A1.‎ 由AA1＝AC＝CB＝2，AB＝2 得∠ACB＝90°，CD＝，A1D＝，DE＝，A1E＝3，‎ 故A1D2＋DE2＝A1E2，即DE⊥A1D.‎ 所以VC－A1DE＝××××＝1.‎ ‎19．G4，G5[2013·山东卷] 如图1－5，四棱锥P—ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．‎ ‎(1)求证：CE∥平面PAD；‎ ‎(2)求证：平面EFG⊥平面EMN.‎ 图1－6‎ ‎19．证明：(1)证法一：取PA的中点H，联结EH，DH.‎ 因为E为PB的中点，‎ 所以EH∥AB，EH＝AB.‎ 又AB∥CD，CD＝AB，‎ 所以EH∥CD，EH＝CD.‎ 因此四边形DCEH是平行四边形．‎ 所以CE∥DH.‎ 又DH平面PAD，CE平面PAD，‎ 因此CE∥平面PAD.‎ 证法二：联结CF.‎ 因为F为AB的中点，‎ 所以AF＝AB.‎ 又CD＝AB，‎ 所以AF＝CD.‎ 又AF∥CD，‎ 所以四边形AFCD为平行四边形．‎ 因此CF∥AD.‎ 又CF平面PAD，‎ 所以CF∥平面PAD.‎ 因为E，F分别为PB，AB的中点，‎ 所以EF∥PA.‎ 又EF平面PAD，‎ 所以EF∥平面PAD.‎ 因为CF∩EF＝F，‎ 故平面CEF∥平面PAD.‎ 又CE平面CEF，‎ 所以CE∥平面PAD.‎ ‎(2)因为E，F分别为PB，AB的中点，‎ 所以EF∥PA.‎ 又AB⊥PA，‎ 所以AB⊥EF.‎ 同理可证AB⊥FG.‎ 又EF∩FG＝F，EF平面EFG，FG平面EFG，‎ 因此AB⊥平面EFG.‎ 又M，N分别为PD，PC的中点，‎ 所以MN∥CD.‎ 又AB∥CD，‎ 所以MN∥AB，‎ 因此MN⊥平面EFG.‎ 又MN平面EMN，‎ 所以平面EFG⊥平面EMN.‎ ‎18．G4，G11[2013·陕西卷] 如图1－5，四棱柱ABCD－A1B‎1C1D1的底面ABCD是正方形，O是底面中心，A1O⊥底面ABCD，AB＝AA1＝.‎ 图1－5‎ ‎(1)证明：平面A1BD∥平面CD1B1；‎ ‎(2)求三棱柱ABD－A1B1D1的体积．‎ ‎18．解： (1)证明：由题设知，BB1‎ 瘙
綊DD1，‎ ‎∴四边形BB1D1D是平行四边形，‎ ‎∴BD∥B1D1.‎ 又BD平面CD1B1，‎ ‎∴BD∥平面CD1B1.‎ ‎∵A1D1‎ 瘙
綊B‎1C1‎ 瘙
綊BC，‎ ‎∴四边形A1BCD1是平行四边形，‎ ‎∴A1B∥D‎1C.‎ 又A1B平面CD1B1，‎ ‎∴A1B∥平面CD1B1.‎ 又∵BD∩A1B＝B，‎ ‎∴平面A1BD∥平面CD1B1.‎ ‎(2)∵A1O⊥平面ABCD，‎ ‎∴A1O是三棱柱ABD－A1B1D1的高．‎ 又∵AO＝AC＝1，AA1＝，‎ ‎∴A1O＝＝1，‎ 又∵S△ABD＝××＝1，‎ ‎∴VABD－A1B1D1＝S△ABD·A1O＝1.‎ ‎19．G4，G5，G7，G11[2013·四川卷] ‎ 图1－8‎ 如图1－8，在三棱柱ABC－A1B‎1C1中，侧棱AA1⊥底面ABC，AB＝AC＝2AA1＝2，∠BAC＝120°，D，D1分别是线段BC，B‎1C1的中点，P是线段AD上异于端点的点．‎ ‎(1)在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD‎1A1；‎ ‎(2)设(1)中的直线l交AC于点Q，求三棱锥A1－QC1D的体积．(锥体体积公式：V＝Sh，其中S为底面面积，h为高)‎ ‎19．解：(1)如图，在平面ABC内，过点P作直线l∥BC，因为l在平面A1BC外，BC在平面A1BC内，由直线与平面平行的判定定理可知，l∥平面A1BC.‎ 由已知，AB＝AC，D是BC的中点，‎ 所以，BC⊥AD，则直线l⊥AD.‎ 因此AA1⊥平面ABC，所以AA1⊥直线l.‎ 又因为AD，AA1在平面ADD‎1A1内，且AD与AA1相交，‎ 所以直线l⊥平面ADD‎1A1.‎ ‎(2)过D作DE⊥AC于E.‎ 因为AA1⊥平面ABC，所以DE⊥AA1.‎ 又因为AC，AA1在平面AA‎1C1C内，且AC与AA1相交，‎ 所以DE⊥平面AA‎1C1C.‎ 由AB＝AC＝2，∠BAC＝120°，有AD＝1，∠DAC＝60°，‎ 所以在△ACD中，DE＝AD＝.‎ 又S△A1QC1＝A‎1C1·AA1＝1，所以 VA1－QC1D＝VD－A1QC1＝DE·S△A1QC1＝××1＝.‎ 因此三棱锥A1－QC1D的体积是.‎ ‎17．G4，G5、G11[2013·天津卷] 如图1－3所示，三棱柱ABC－A1B‎1C1中，侧棱A‎1A⊥底面ABC，且各棱长均相等，D，E，F分别为棱AB，BC，A‎1C1的中点．‎ ‎(1)证明EF∥平面A1CD；‎ ‎(2)证明平面A1CD⊥平面A1ABB1；‎ ‎(3)求直线BC与平面A1CD所成角的正弦值．‎ 图1－3‎ ‎17．解：(1)证明：如图，在三棱柱ABC－A1B‎1C1中，AC∥A‎1C1，且AC＝A‎1C1，联结ED，在△ABC中，因为D，E分别为AB，BC的中点，所以DE＝AC且DE∥AC，又因为F为A‎1C1的中点，可得A‎1F＝DE，且A‎1F∥DE，即四边形A1DEF为平行四边形，所以EF∥DA1.又EF平面A1CD，DA1平面A1CD，所以，EF∥平面A1CD.‎ ‎(2)证明：由于底面ABC是正三角形，D为AB的中点，故CD⊥AB，又由于侧棱AA1⊥底面ABC，CD平面ABC，所以A‎1A⊥CD，又A‎1A∩AB＝A，因此CD⊥平面A1ABB1，而CD平面A1CD，所以平面A1CD⊥平面A1ABB1.‎ ‎(3)在平面A1ABB1内，过点B作BG⊥A1D交直线A1D于点G，联结CG，由于平面A1CD⊥平面A1ABB1，而直线A1D是平面A1CD与平面A1ABB1的交线，故BG⊥平面A1CD，由此得∠BCG为直线BC与平面A1CD所成的角．‎ 设三棱柱各棱长为a，可得A1D＝，由△A1AD∽△BGD，易得BG＝.在Rt△BGC中，sin∠BCG＝＝.‎ 所以直线BC与平面A1CD所成角的正弦值为.‎ ‎4．G4，G5[2013·浙江卷] 设m，n是两条不同的直线，α，β是两个不同的平面(　　)‎ A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥β C．若m∥n，m⊥α，则n⊥α D．若m∥α，α⊥β，则m⊥β ‎4．C　[解析] 对于选项C，若m∥n，m⊥α，易得n⊥α.所以选择C.‎ G5　空间中的垂直关系　　　　　　　　　　　　　　　　　　　‎ 图1－5‎ ‎18．G5[2013·安徽卷] 如图1－5，四棱锥P－ABCD的底面ABCD是边长为2的菱形，∠BAD＝60°，已知PB＝PD＝2，PA＝.‎ ‎(1)证明：PC⊥BD；‎ ‎(2)若E为PA的中点，求三棱锥P－BCE的体积．‎ ‎18．解：(1)证明：联结AC，交BD于O点，联结PO.‎ 因为底面ABCD是菱形，所以AC⊥BD，BO＝DO.‎ 由PB＝PD知，PO⊥BD.再由PO∩AC＝O知，BD⊥面APC，又PC平面APC，因此BD⊥PC.‎ ‎(2)因为E是PA的中点，所以VP－BCE＝VC－PEB＝‎ VC－PAB＝VB－APC.‎ 由PB＝PD＝AB＝AD＝2知，△ABD≌△PBD.‎ 因为∠BAD＝60°，‎ 所以PO＝AO＝，AC＝2，BO＝1.又PA＝，故PO2＋AO2＝PA2，即PO⊥AC.‎ 故S△APC＝PO·AC＝3.‎ 由(1)知，BO⊥面APC，因此VP－BCE＝VB－APC＝··S△APC·BO＝.‎ ‎17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：‎ ‎(1)PA⊥底面ABCD；‎ ‎(2)BE∥平面PAD；‎ ‎(3)平面BEF⊥平面PCD.‎ 图1－5‎ ‎17．证明：(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD.‎ ‎(2)因为AB∥CD，CD＝2AB，E为CD的中点，‎ 所以AB∥DE，且AB＝DE，‎ 所以ABED为平行四边形，‎ 所以BE∥AD.‎ 又因为BE平面PAD，AD平面PAD，‎ 所以BE∥平面PAD.‎ ‎(3)因为AB⊥AD，而且ABED为平行四边形，‎ 所以BE⊥CD，AD⊥CD.‎ 由(1)知PA⊥底面ABCD，‎ 所以PA⊥CD.‎ 又因为AD∩PA＝A，所以CD⊥平面PAD，‎ 所以CD⊥PD.‎ 因为E和F分别是CD和PC的中点，‎ 所以PD∥EF，‎ 所以CD⊥EF，‎ 所以CD⊥平面BEF，‎ 所以平面BEF⊥平面PCD.‎ ‎19．G5、G11[2013·全国卷] 如图1－3所示，四棱锥P—ABCD中，∠ABC＝∠BAD＝90°，BC＝2AD，△PAB和△PAD都是边长为2的等边三角形．‎ 图1－3‎ ‎(1)证明：PB⊥CD；‎ ‎(2)求点A到平面PCD的距离．‎ ‎19．解：(1)证明：取BC的中点E，联结DE，则四边形ABED为正方形．过P作PO⊥平面ABCD，垂足为O.联结OA，OB，OD，OE.由△PAB和△PAD都是等边三角形知PA＝PB＝PD，‎ 所以OA＝OB＝OD，即点O为正方形ABED对角线的交点．故OE⊥BD，从而PB⊥OE.因为O是BD的中点，E是BC的中点，所以OE∥CD.‎ 因此PB⊥CD.‎ ‎(2)取PD的中点F，联结OF，则OF∥PB.‎ 由(1)知，PB⊥CD，故OF⊥CD.‎ 又OD＝BD＝，OP＝＝，‎ 故△POD为等腰三角形，因此OF⊥PD.‎ 又PD∩CD＝D，所以OF⊥平面PCD.‎ 因为AE∥CD，CD平面PCD，AE平面PCD，所以AE∥平面PCD.‎ 因此O到平面PCD的距离OF就是A到平面PCD的距离，而OF＝PB＝1，‎ 所以点A到平面PCD的距离为1.‎ ‎18．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC中，D，E分别是AB，AC上的点，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图1－4(2)所示的三棱锥A－BCF，其中BC＝.‎ 图1－4‎ ‎(1)证明：DE∥平面BCF；‎ ‎(2)证明：CF⊥平面ABF；‎ ‎(3)当AD＝时，求三棱锥F－DEG的体积．‎ ‎18．解：‎ ‎8．G4、G5[2013·广东卷] 设l为直线，α，β是两个不同的平面，下列命题中正确的是(　　)‎ A．若l∥α，l∥β，则α∥β B．若l⊥α，l⊥β，则α∥β C．若l⊥α，l∥β，则α∥β D．若α⊥β，l∥α，则l⊥β ‎8．B　[解析] 根据空间平行、垂直关系的判定和性质，易知选B.‎ ‎16．G4，G5[2013·江苏卷] 如图1－2，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．‎ 求证：(1)平面EFG∥平面ABC；‎ ‎(2)BC⊥SA.‎ 图1－2‎ ‎16．证明：(1)因为AS＝AB，AF⊥SB，垂足为F，所以F是SB的中点．又因为E是SA的中点，所以EF∥AB.‎ 因为EF平面ABC，AB平面ABC，‎ 所以EF∥平面ABC.‎ 同理EG∥平面ABC.又EF∩EG＝E，‎ 所以平面EFG∥平面ABC.‎ ‎(2)因为平面SAB⊥平面SBC，且交线为SB，‎ 又AF平面SAB，AF⊥SB，‎ 所以AF⊥平面SBC.‎ 因为BC平面SBC，所以AF⊥BC.‎ 又因为AB⊥BC，AF∩AB＝A，AF，AB平面SAB，所以BC⊥平面SAB.‎ 因为SA平面SAB，所以BC⊥SA.‎ ‎19．G5，G7[2013·江西卷] 如图1－7所示，直四棱柱ABCD－A1B‎1C1D1中，AB∥CD，AD⊥AB，AB＝2，AD＝，AA1＝3，E为CD上一点，DE＝1，EC＝3.‎ ‎(1)证明：BE⊥平面BB‎1C1C；‎ ‎(2)求点B1到平面EA‎1C1的距离．‎ 图1－7‎ ‎19．解：(1)证明：过B作CD的垂线交CD于F，则BF＝AD＝，EF＝AB－DE＝1，FC＝2.‎ 在Rt△BEF中，BE＝.‎ 在Rt△CFB中，BC＝.‎ 在△BEC中，因为BE2＋BC2＝9＝EC2，故BE⊥BC.‎ 由BB1⊥平面ABCD得BE⊥BB1.‎ 所以BE⊥平面BB‎1C1C.‎ ‎(2)三棱锥E－A1B‎1C1的体积V＝·AA1·S△A1B‎1C1＝.‎ 在Rt△A1D‎1C1中，A‎1C1＝＝3 .‎ 同理，EC1＝＝3 ，A1E＝＝2 .‎ 故S△A‎1C1E＝3 .‎ 设点B1到平面EA‎1C1的距离为d，则三棱锥B1－A‎1C1E的体积 V＝·d·S△A‎1C1E＝d，‎ 从而d＝，d＝.‎ 图1－4‎ ‎18．G4，G5[2013·辽宁卷] 如图1－4，AB是圆O的直径，PA垂直圆O所在的平面，C是圆O上的点．‎ ‎(1)求证：BC⊥平面PAC；‎ ‎(2)设Q为PA的中点，G为△AOC的重心，求证：QG∥平面PBC.‎ ‎18．证明：(1)由AB是圆O的直径，得AC⊥BC.‎ 由PA⊥平面ABC，BC平面ABC，得PA⊥BC.‎ 又PA∩AC＝A，PA平面PAC，AC平面PAC，‎ 所以BC⊥平面PAC.‎ ‎(2)联结OG并延长交AC于M，联结QM，QO，‎ 由G为△AOC的重心，得M为AC中点，‎ 由Q为PA中点，得QM∥PC.‎ 又O为AB中点，得OM∥BC.‎ 因为QM∩MO＝M，QM平面QMO.‎ MO平面QMO，‎ BC∩PC＝C，BC平面PBC，PC平面PBC，‎ 所以平面QMO∥平面PBC.‎ 因为QG平面QMO，‎ 所以QG∥平面PBC.‎ ‎19．G4，G5[2013·山东卷] 如图1－5，四棱锥P—ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．‎ ‎(1)求证：CE∥平面PAD；‎ ‎(2)求证：平面EFG⊥平面EMN.‎ 图1－6‎ ‎19．证明：(1)证法一：取PA的中点H，联结EH，DH.‎ 因为E为PB的中点，‎ 所以EH∥AB，EH＝AB.‎ 又AB∥CD，CD＝AB，‎ 所以EH∥CD，EH＝CD.‎ 因此四边形DCEH是平行四边形．‎ 所以CE∥DH.‎ 又DH平面PAD，CE平面PAD，‎ 因此CE∥平面PAD.‎ 证法二：联结CF.‎ 因为F为AB的中点，‎ 所以AF＝AB.‎ 又CD＝AB，‎ 所以AF＝CD.‎ 又AF∥CD，‎ 所以四边形AFCD为平行四边形．‎ 因此CF∥AD.‎ 又CF平面PAD，‎ 所以CF∥平面PAD.‎ 因为E，F分别为PB，AB的中点，‎ 所以EF∥PA.‎ 又EF平面PAD，‎ 所以EF∥平面PAD.‎ 因为CF∩EF＝F，‎ 故平面CEF∥平面PAD.‎ 又CE平面CEF，‎ 所以CE∥平面PAD.‎ ‎(2)因为E，F分别为PB，AB的中点，‎ 所以EF∥PA.‎ 又AB⊥PA，‎ 所以AB⊥EF.‎ 同理可证AB⊥FG.‎ 又EF∩FG＝F，EF平面EFG，FG平面EFG，‎ 因此AB⊥平面EFG.‎ 又M，N分别为PD，PC的中点，‎ 所以MN∥CD.‎ 又AB∥CD，‎ 所以MN∥AB，‎ 因此MN⊥平面EFG.‎ 又MN平面EMN，‎ 所以平面EFG⊥平面EMN.‎ ‎19．G4，G5，G7，G11[2013·四川卷] ‎ 图1－8‎ 如图1－8，在三棱柱ABC－A1B‎1C1中，侧棱AA1⊥底面ABC，AB＝AC＝2AA1＝2，∠BAC＝120°，D，D1分别是线段BC，B‎1C1的中点，P是线段AD上异于端点的点．‎ ‎(1)在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD‎1A1；‎ ‎(2)设(1)中的直线l交AC于点Q，求三棱锥A1－QC1D的体积．(锥体体积公式：V＝Sh，其中S为底面面积，h为高)‎ ‎19．解：(1)如图，在平面ABC内，过点P作直线l∥BC，因为l在平面A1BC外，BC在平面A1BC内，由直线与平面平行的判定定理可知，l∥平面A1BC.‎ 由已知，AB＝AC，D是BC的中点，‎ 所以，BC⊥AD，则直线l⊥AD.‎ 因此AA1⊥平面ABC，所以AA1⊥直线l.‎ 又因为AD，AA1在平面ADD‎1A1内，且AD与AA1相交，‎ 所以直线l⊥平面ADD‎1A1.‎ ‎(2)过D作DE⊥AC于E.‎ 因为AA1⊥平面ABC，所以DE⊥AA1.‎ 又因为AC，AA1在平面AA‎1C1C内，且AC与AA1相交，‎ 所以DE⊥平面AA‎1C1C.‎ 由AB＝AC＝2，∠BAC＝120°，有AD＝1，∠DAC＝60°，‎ 所以在△ACD中，DE＝AD＝.‎ 又S△A1QC1＝A‎1C1·AA1＝1，所以 VA1－QC1D＝VD－A1QC1＝DE·S△A1QC1＝××1＝.‎ 因此三棱锥A1－QC1D的体积是.‎ ‎17．G4，G5、G11[2013·天津卷] 如图1－3所示，三棱柱ABC－A1B‎1C1中，侧棱A‎1A⊥底面ABC，且各棱长均相等，D，E，F分别为棱AB，BC，A‎1C1的中点．‎ ‎(1)证明EF∥平面A1CD；‎ ‎(2)证明平面A1CD⊥平面A1ABB1；‎ ‎(3)求直线BC与平面A1CD所成角的正弦值．‎ 图1－3‎ ‎17．解：(1)证明：如图，在三棱柱ABC－A1B‎1C1中，AC∥A‎1C1，且AC＝A‎1C1，联结ED，在△ABC中，因为D，E分别为AB，BC的中点，所以DE＝AC且DE∥AC，又因为F为A‎1C1的中点，可得A‎1F＝DE，且A‎1F∥DE，即四边形A1DEF为平行四边形，所以EF∥DA1.又EF平面A1CD，DA1平面A1CD，所以，EF∥平面A1CD.‎ ‎(2)证明：由于底面ABC是正三角形，D为AB的中点，故CD⊥AB，又由于侧棱AA1⊥底面ABC，CD平面ABC，所以A‎1A⊥CD，又A‎1A∩AB＝A，因此CD⊥平面A1ABB1，而CD平面A1CD，所以平面A1CD⊥平面A1ABB1.‎ ‎(3)在平面A1ABB1内，过点B作BG⊥A1D交直线A1D于点G，联结CG，由于平面A1CD⊥平面A1ABB1，而直线A1D是平面A1CD与平面A1ABB1的交线，故BG⊥平面A1CD，由此得∠BCG为直线BC与平面A1CD所成的角．‎ 设三棱柱各棱长为a，可得A1D＝，由△A1AD∽△BGD，易得BG＝.在Rt△BGC中，sin∠BCG＝＝.‎ 所以直线BC与平面A1CD所成角的正弦值为.‎ ‎19．G5[2013·新课标全国卷Ⅰ] 如图1－5所示，三棱柱ABC－A1B‎1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.‎ ‎(1)证明：AB⊥A‎1C；‎ ‎(2)若AB＝CB＝2，A‎1C＝，求三棱柱ABC－A1B‎1C1的体积．‎ 图1－5‎ ‎19．解：(1)取AB的中点O，联结OC，OA1，A1B，‎ 因为CA＝CB，所以OC⊥AB.‎ 由于AB＝AA1，∠BAA1＝60°，故△AA1B为等边三角形，所以OA1⊥AB.‎ 因为OC∩OA1＝O，所以AB⊥平面OA‎1C.‎ 又A‎1C平面OA‎1C，故AB⊥A‎1C.‎ ‎(2)由题设知△ABC与△AA1B都是边长为2的等边三角形，所以OC＝OA1＝.‎ 又A‎1C＝，则A‎1C2＝OC2＋OA，故OA1⊥OC.‎ 因为OC∩AB＝O，所以OA1⊥平面ABC，OA1为三棱柱ABC－A1B‎1C1的高．‎ 又△ABC的面积S△ABC＝，故三棱柱ABC－A1B‎1C1的体积V＝S△ABC·OA1＝3.‎ ‎4．G4，G5[2013·浙江卷] 设m，n是两条不同的直线，α，β是两个不同的平面(　　)‎ A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥β C．若m∥n，m⊥α，则n⊥α D．若m∥α，α⊥β，则m⊥β ‎4．C　[解析] 对于选项C，若m∥n，m⊥α，易得n⊥α.所以选择C.‎ ‎19．G2和G5[2013·重庆卷] 如图1－4所示，四棱锥P－ABCD中，PA⊥底面ABCD，PA＝2 ，BC＝CD＝2，∠ACB＝∠ACD＝.‎ ‎(1)求证：BD⊥平面PAC；‎ ‎(2)若侧棱PC上的点F满足PF＝7FC，求三棱锥P－BDF的体积．‎ 图1－4‎ ‎19．解：(1)证明：因为BC＝CD，即△BCD为等腰三角形，又∠ACB＝∠ACD，故BD⊥AC.‎ 因为PA⊥底面ABCD，所以PA⊥BD，从而BD与平面PAC内两条相交直线PA，AC都垂直，所以BD⊥平面PAC.‎ ‎(2)三棱锥P－BCD的底面BCD的面积S△BCD＝BC·CD·sin∠BCD＝·2·2·sin＝.‎ 由PA⊥底面ABCD，得 VP－BCD＝·S△BCD·PA＝××2 ＝2.‎ 由PF＝7FC，得三棱锥F－BCD的高为PA，故VF－BCD＝·S△BCD·PA＝×××2 ＝，‎ 所以VP－BDF＝VP－BCD－VF－BCD＝2－＝.‎ G6　三垂线定理　　　　　　　　　　　　　　　　　　　‎ ‎8．G1，G6[2013·北京卷] 如图1－2，在正方体ABCD－A1B‎1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有(　　)‎ 图1－2‎ A．3个 B．4个 C．5个 D．6个 ‎8．B　[解析] 设棱长为1，∵BD1＝，∴BP＝，D1P＝.联结AD1，B1D1，CD1，得△ABD1≌△CBD1≌△B1BD1，‎ ‎∴∠ABD1＝∠CBD1＝∠B1BD1，且cos∠ABD1＝，‎ 联结AP，PC，PB1，则有△ABP≌△CBP≌△B1BP，‎ ‎∴AP＝CP＝B1P＝，同理DP＝A1P＝C1P＝1，‎ ‎∴P到各顶点的距离的不同取值有4个．‎ G7　棱柱与棱锥　　　　　　　　　　　　　　　　　　　‎ ‎17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：‎ ‎(1)PA⊥底面ABCD；‎ ‎(2)BE∥平面PAD；‎ ‎(3)平面BEF⊥平面PCD.‎ 图1－5‎ ‎17．证明：(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD.‎ ‎(2)因为AB∥CD，CD＝2AB，E为CD的中点，‎ 所以AB∥DE，且AB＝DE，‎ 所以ABED为平行四边形，‎ 所以BE∥AD.‎ 又因为BE平面PAD，AD平面PAD，‎ 所以BE∥平面PAD.‎ ‎(3)因为AB⊥AD，而且ABED为平行四边形，‎ 所以BE⊥CD，AD⊥CD.‎ 由(1)知PA⊥底面ABCD，‎ 所以PA⊥CD.‎ 又因为AD∩PA＝A，所以CD⊥平面PAD，‎ 所以CD⊥PD.‎ 因为E和F分别是CD和PC的中点，‎ 所以PD∥EF，‎ 所以CD⊥EF，‎ 所以CD⊥平面BEF，‎ 所以平面BEF⊥平面PCD.‎ ‎10．G2，G7[2013·北京卷] 某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．‎ 图1－3‎ ‎10．3　[解析] 正视图的长为3，侧视图的长为3，因此，该四棱锥底面是边长为3的正方形，且高为1，因此V＝×(3×3)×1＝3.‎ ‎8．G7[2013·江苏卷] 如图1－1，在三棱柱A1B‎1C1－ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F－ADE的体积为V1，三棱柱A1B‎1C1－ABC的体积为V2，则V1∶V2＝________．‎ 图1－1‎ ‎8．1∶24　[解析] 设三棱柱的底面积为S，高为h，则V2＝Sh，又D，E，F分别为AB，AC，AA1的中点，所以S△AED＝S，且三棱锥F－ADE的高为h，故V1＝S△AED·h＝·S·h＝Sh，所以V1∶V2＝1∶24.‎ ‎19．G5，G7[2013·江西卷] 如图1－7所示，直四棱柱ABCD－A1B‎1C1D1中，AB∥CD，AD⊥AB，AB＝2，AD＝，AA1＝3，E为CD上一点，DE＝1，EC＝3.‎ ‎(1)证明：BE⊥平面BB‎1C1C；‎ ‎(2)求点B1到平面EA‎1C1的距离．‎ 图1－7‎ ‎19．解：(1)证明：过B作CD的垂线交CD于F，则BF＝AD＝，EF＝AB－DE＝1，FC＝2.‎ 在Rt△BEF中，BE＝.‎ 在Rt△CFB中，BC＝.‎ 在△BEC中，因为BE2＋BC2＝9＝EC2，故BE⊥BC.‎ 由BB1⊥平面ABCD得BE⊥BB1.‎ 所以BE⊥平面BB‎1C1C.‎ ‎(2)三棱锥E－A1B‎1C1的体积V＝·AA1·S△A1B‎1C1＝.‎ 在Rt△A1D‎1C1中，A‎1C1＝＝3 .‎ 同理，EC1＝＝3 ，A1E＝＝2 .‎ 故S△A‎1C1E＝3 .‎ 设点B1到平面EA‎1C1的距离为d，则三棱锥B1－A‎1C1E的体积 V＝·d·S△A‎1C1E＝d，‎ 从而d＝，d＝.‎ ‎18．G4，G7，G11[2013·新课标全国卷Ⅱ] 如图，直三棱柱ABC－A1B‎1C1中，D，E分别是AB，BB1的中点．‎ ‎(1)证明：BC1∥平面A1CD；‎ ‎(2)设AA1＝AC＝CB＝2，AB＝2，求三棱锥C－A1DE的体积．‎ 图1－7‎ ‎18．解：(1)证明：联结AC1交A‎1C于点F，则F为AC1中点．又D是AB中点，联结DF，则BC1∥DF.因为DF平面A1CD，BC1平面A1CD，所以BC1∥平面A1CD.‎ 图1－8‎ ‎(2)因为ABC－A1B‎1C1是直三棱柱，所以AA1⊥CD.由已知AC＝CB，D为AB的中点，所以CD⊥AB.又AA1∩AB＝A，于是CD⊥平面ABB‎1A1.‎ 由AA1＝AC＝CB＝2，AB＝2 得∠ACB＝90°，CD＝，A1D＝，DE＝，A1E＝3，‎ 故A1D2＋DE2＝A1E2，即DE⊥A1D.‎ 所以VC－A1DE＝××××＝1.‎ ‎19．G4，G5，G7，G11[2013·四川卷] ‎ 图1－8‎ 如图1－8，在三棱柱ABC－A1B‎1C1中，侧棱AA1⊥底面ABC，AB＝AC＝2AA1＝2，∠BAC＝120°，D，D1分别是线段BC，B‎1C1的中点，P是线段AD上异于端点的点．‎ ‎(1)在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD‎1A1；‎ ‎(2)设(1)中的直线l交AC于点Q，求三棱锥A1－QC1D的体积．(锥体体积公式：V＝Sh，其中S为底面面积，h为高)‎ ‎19．解：(1)如图，在平面ABC内，过点P作直线l∥BC，因为l在平面A1BC外，BC在平面A1BC内，由直线与平面平行的判定定理可知，l∥平面A1BC.‎ 由已知，AB＝AC，D是BC的中点，‎ 所以，BC⊥AD，则直线l⊥AD.‎ 因此AA1⊥平面ABC，所以AA1⊥直线l.‎ 又因为AD，AA1在平面ADD‎1A1内，且AD与AA1相交，‎ 所以直线l⊥平面ADD‎1A1.‎ ‎(2)过D作DE⊥AC于E.‎ 因为AA1⊥平面ABC，所以DE⊥AA1.‎ 又因为AC，AA1在平面AA‎1C1C内，且AC与AA1相交，‎ 所以DE⊥平面AA‎1C1C.‎ 由AB＝AC＝2，∠BAC＝120°，有AD＝1，∠DAC＝60°，‎ 所以在△ACD中，DE＝AD＝.‎ 又S△A1QC1＝A‎1C1·AA1＝1，所以 VA1－QC1D＝VD－A1QC1＝DE·S△A1QC1＝××1＝.‎ 因此三棱锥A1－QC1D的体积是.‎ ‎8．G2和G7[2013·重庆卷] 某几何体的三视图如图1－3所示，则该几何体的表面积为(　　)‎ 图1－3‎ A．180 B．‎200 C．220 D．240‎ ‎8．D　[解析] 该几何体为直四棱柱，其高为10，底面是上底为2，下底为8，高为4，其腰为5的等腰梯形，所以底面面积和为(2＋8)×4×2＝40.四个侧面的面积和为(2＋8＋5×2)×10＝200，所以该直四棱柱的表面积为S＝40＋200＝240，故选D.‎ G8　多面体与球　　　　　　　　　　　　　　　　　　　‎ ‎10．G8[2013·天津卷] 已知一个正方体的所有顶点在一个球面上，若球的体积为，则正方体的棱长为________．‎ ‎10.　[解析] 设正方体的棱长为a，则π＝π，解之得a＝.‎ ‎15．G8[2013·新课标全国卷Ⅱ] 已知正四棱锥O－ABCD的体积为，底面边长为，则以O为球心，OA为半径的球的表面积为________．‎ ‎15．24π　[解析] 设O到底面的距离为h，则×3×h＝h＝，OA＝＝，故球的表面积为4π×()2＝24π.‎ ‎16．G8[2013·湖北卷] 我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸．若盆中积水深九寸，则平地降雨量是________寸．‎ ‎(注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸)‎ ‎16．3　[解析] 积水深度为盆深的一半，故此时积水部分的圆台上底面直径为二尺，圆台的高为九寸，故此时积水的体积是π(102＋62＋10×6)×9＝196×3π(立方寸)，盆口的面积是π×142＝196π，所以平均降雨量是＝3寸．‎ ‎15．G8[2013·新课标全国卷Ⅰ] 已知H是球O的直径AB上一点，AH∶HB＝1∶2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为________．‎ ‎15.　[解析] 截面为圆，由已知得该圆的半径为1.设球的半径为r，则AH＝r，所以OH＝r，所以r2＋12＝r2，r2＝，所以球的表面积是4πr2＝.‎ G9　空间向量及运算　　　　　　　　　　　　　　　　　　　‎ G10　空间向量解决线面位置关系　　　　　　　　　　　　　　　　　　　‎ G11　空间有与距离的求法　　　　　　　　　　　　　　　　　　　‎ ‎19．G5、G11[2013·全国卷] 如图1－3所示，四棱锥P—ABCD中，∠ABC＝∠BAD＝90°，BC＝2AD，△PAB和△PAD都是边长为2的等边三角形．‎ 图1－3‎ ‎(1)证明：PB⊥CD；‎ ‎(2)求点A到平面PCD的距离．‎ ‎19．解：(1)证明：取BC的中点E，联结DE，则四边形ABED为正方形．过P作PO⊥平面ABCD，垂足为O.联结OA，OB，OD，OE.由△PAB和△PAD都是等边三角形知PA＝PB＝PD，‎ 所以OA＝OB＝OD，即点O为正方形ABED对角线的交点．故OE⊥BD，从而PB⊥OE.因为O是BD的中点，E是BC的中点，所以OE∥CD.‎ 因此PB⊥CD.‎ ‎(2)取PD的中点F，联结OF，则OF∥PB.‎ 由(1)知，PB⊥CD，故OF⊥CD.‎ 又OD＝BD＝，OP＝＝，‎ 故△POD为等腰三角形，因此OF⊥PD.‎ 又PD∩CD＝D，所以OF⊥平面PCD.‎ 因为AE∥CD，CD平面PCD，AE平面PCD，所以AE∥平面PCD.‎ 因此O到平面PCD的距离OF就是A到平面PCD的距离，而OF＝PB＝1，‎ 所以点A到平面PCD的距离为1.‎ ‎11．G11[2013·全国卷] 已知正四棱柱ABCD－A1B‎1C1D1中，AA1＝2AB，则CD与平面BDC1所成角的正弦值等于(　　)‎ A. B. C. D. ‎11．A　[解析] 如图，联结AC，交BD于点O.由于BO⊥OC，BO⊥CC1，可得BO⊥平面OCC1，从而平面OCC1⊥平面BDC1，过点C作OC1的垂线交OC1于点E，根据面面垂直的性质定理可得CE⊥平面BDC1，∠CDE即为所求的线面角．设AB＝2，则OC＝，OC1＝＝3，所以CE＝＝＝，所以sin ∠CDE＝＝.‎ ‎22．G11[2013·江苏卷] 如图1－2所示，在直三棱柱A1B‎1C1－ABC中，AB⊥AC，AB＝AC＝2，A‎1A＝4，点D是BC的中点．‎ ‎(1)求异面直线A1B与C1D所成角的余弦值；‎ ‎(2)求平面ADC1与平面ABA1所成二面角的正弦值．‎ 图1－2‎ ‎22．解：(1)以A为坐标原点，建立如图所示的空间直角坐标系A－xyz，则A(0，0，0)，B(2，0，0)，C(0，2，0)，D(1，1，0)，A1(0，0，4)，‎ C1(0，2，4)，所以＝(2，0，－4)，＝(1，－1，－4)．‎ 因为cos〈，〉＝＝＝，所以异面直线A1B与C1D所成角的余弦值为.‎ ‎(2)设平面ADC1的法向量为n1＝(x，y，z)，因为＝(1，1，0)，＝(0，2，4)，所以n1·＝0，n1·＝0，即x＋y＝0且y＋2z＝0，取z＝1，得x＝2，y＝－2，所以，n1＝(2，－2，1)是平面ADC1的一个法向量．取平面AA1B的一个法向量为n2＝(0，1，0)，设平面ADC1与平面ABA1所成二面角的大小为θ.‎ 由|cos θ|＝＝＝，得sin θ＝.‎ 因此，平面ADC1与平面ABA1所成二面角的正弦值为.‎ ‎18．G4，G7，G11[2013·新课标全国卷Ⅱ] 如图，直三棱柱ABC－A1B‎1C1中，D，E分别是AB，BB1的中点．‎ ‎(1)证明：BC1∥平面A1CD；‎ ‎(2)设AA1＝AC＝CB＝2，AB＝2，求三棱锥C－A1DE的体积．‎ 图1－7‎ ‎18．解：(1)证明：联结AC1交A‎1C于点F，则F为AC1中点．又D是AB中点，联结DF，则BC1∥DF.因为DF平面A1CD，BC1平面A1CD，所以BC1∥平面A1CD.‎ 图1－8‎ ‎(2)因为ABC－A1B‎1C1是直三棱柱，所以AA1⊥CD.由已知AC＝CB，D为AB的中点，所以CD⊥AB.又AA1∩AB＝A，于是CD⊥平面ABB‎1A1.‎ 由AA1＝AC＝CB＝2，AB＝2 得∠ACB＝90°，CD＝，A1D＝，DE＝，A1E＝3，‎ 故A1D2＋DE2＝A1E2，即DE⊥A1D.‎ 所以VC－A1DE＝××××＝1.‎ ‎18．G4，G11[2013·陕西卷] 如图1－5，四棱柱ABCD－A1B‎1C1D1的底面ABCD是正方形，O是底面中心，A1O⊥底面ABCD，AB＝AA1＝.‎ 图1－5‎ ‎(1)证明：平面A1BD∥平面CD1B1；‎ ‎(2)求三棱柱ABD－A1B1D1的体积．‎ ‎18．解： (1)证明：由题设知，BB1‎ 瘙
綊DD1，‎ ‎∴四边形BB1D1D是平行四边形，‎ ‎∴BD∥B1D1.‎ 又BD平面CD1B1，‎ ‎∴BD∥平面CD1B1.‎ ‎∵A1D1‎ 瘙
綊B‎1C1‎ 瘙
綊BC，‎ ‎∴四边形A1BCD1是平行四边形，‎ ‎∴A1B∥D‎1C.‎ 又A1B平面CD1B1，‎ ‎∴A1B∥平面CD1B1.‎ 又∵BD∩A1B＝B，‎ ‎∴平面A1BD∥平面CD1B1.‎ ‎(2)∵A1O⊥平面ABCD，‎ ‎∴A1O是三棱柱ABD－A1B1D1的高．‎ 又∵AO＝AC＝1，AA1＝，‎ ‎∴A1O＝＝1，‎ 又∵S△ABD＝××＝1，‎ ‎∴VABD－A1B1D1＝S△ABD·A1O＝1.‎ ‎19．G4，G5，G7，G11[2013·四川卷] ‎ 图1－8‎ 如图1－8，在三棱柱ABC－A1B‎1C1中，侧棱AA1⊥底面ABC，AB＝AC＝2AA1＝2，∠BAC＝120°，D，D1分别是线段BC，B‎1C1的中点，P是线段AD上异于端点的点．‎ ‎(1)在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD‎1A1；‎ ‎(2)设(1)中的直线l交AC于点Q，求三棱锥A1－QC1D的体积．(锥体体积公式：V＝Sh，其中S为底面面积，h为高)‎ ‎19．解：(1)如图，在平面ABC内，过点P作直线l∥BC，因为l在平面A1BC外，BC在平面A1BC内，由直线与平面平行的判定定理可知，l∥平面A1BC.‎ 由已知，AB＝AC，D是BC的中点，‎ 所以，BC⊥AD，则直线l⊥AD.‎ 因此AA1⊥平面ABC，所以AA1⊥直线l.‎ 又因为AD，AA1在平面ADD‎1A1内，且AD与AA1相交，‎ 所以直线l⊥平面ADD‎1A1.‎ ‎(2)过D作DE⊥AC于E.‎ 因为AA1⊥平面ABC，所以DE⊥AA1.‎ 又因为AC，AA1在平面AA‎1C1C内，且AC与AA1相交，‎ 所以DE⊥平面AA‎1C1C.‎ 由AB＝AC＝2，∠BAC＝120°，有AD＝1，∠DAC＝60°，‎ 所以在△ACD中，DE＝AD＝.‎ 又S△A1QC1＝A‎1C1·AA1＝1，所以 VA1－QC1D＝VD－A1QC1＝DE·S△A1QC1＝××1＝.‎ 因此三棱锥A1－QC1D的体积是.‎ ‎17．G4，G5、G11[2013·天津卷] 如图1－3所示，三棱柱ABC－A1B‎1C1中，侧棱A‎1A⊥底面ABC，且各棱长均相等，D，E，F分别为棱AB，BC，A‎1C1的中点．‎ ‎(1)证明EF∥平面A1CD；‎ ‎(2)证明平面A1CD⊥平面A1ABB1；‎ ‎(3)求直线BC与平面A1CD所成角的正弦值．‎ 图1－3‎ ‎17．解：(1)证明：如图，在三棱柱ABC－A1B‎1C1中，AC∥A‎1C1，且AC＝A‎1C1，联结ED，在△ABC中，因为D，E分别为AB，BC的中点，所以DE＝AC且DE∥AC，又因为F为A‎1C1的中点，可得A‎1F＝DE，且A‎1F∥DE，即四边形A1DEF为平行四边形，所以EF∥DA1.又EF平面A1CD，DA1平面A1CD，所以，EF∥平面A1CD.‎ ‎(2)证明：由于底面ABC是正三角形，D为AB的中点，故CD⊥AB，又由于侧棱AA1⊥底面ABC，CD平面ABC，所以A‎1A⊥CD，又A‎1A∩AB＝A，因此CD⊥平面A1ABB1，而CD平面A1CD，所以平面A1CD⊥平面A1ABB1.‎ ‎(3)在平面A1ABB1内，过点B作BG⊥A1D交直线A1D于点G，联结CG，由于平面A1CD⊥平面A1ABB1，而直线A1D是平面A1CD与平面A1ABB1的交线，故BG⊥平面A1CD，由此得∠BCG为直线BC与平面A1CD所成的角．‎ 设三棱柱各棱长为a，可得A1D＝，由△A1AD∽△BGD，易得BG＝.在Rt△BGC中，sin∠BCG＝＝.‎ 所以直线BC与平面A1CD所成角的正弦值为.‎ G12　单元综合　　　　　　　　　　　　　　　　　　　‎ 图1－3‎ ‎15．G12[2013·安徽卷] 如图1－3，正方体ABCD－A1B‎1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S，则下列命题正确的是________(写出所有正确命题的编号)．‎ ‎①当00，d3－d1>0，故V－V估>0，即V估