用分离常数法解高考的题 16页

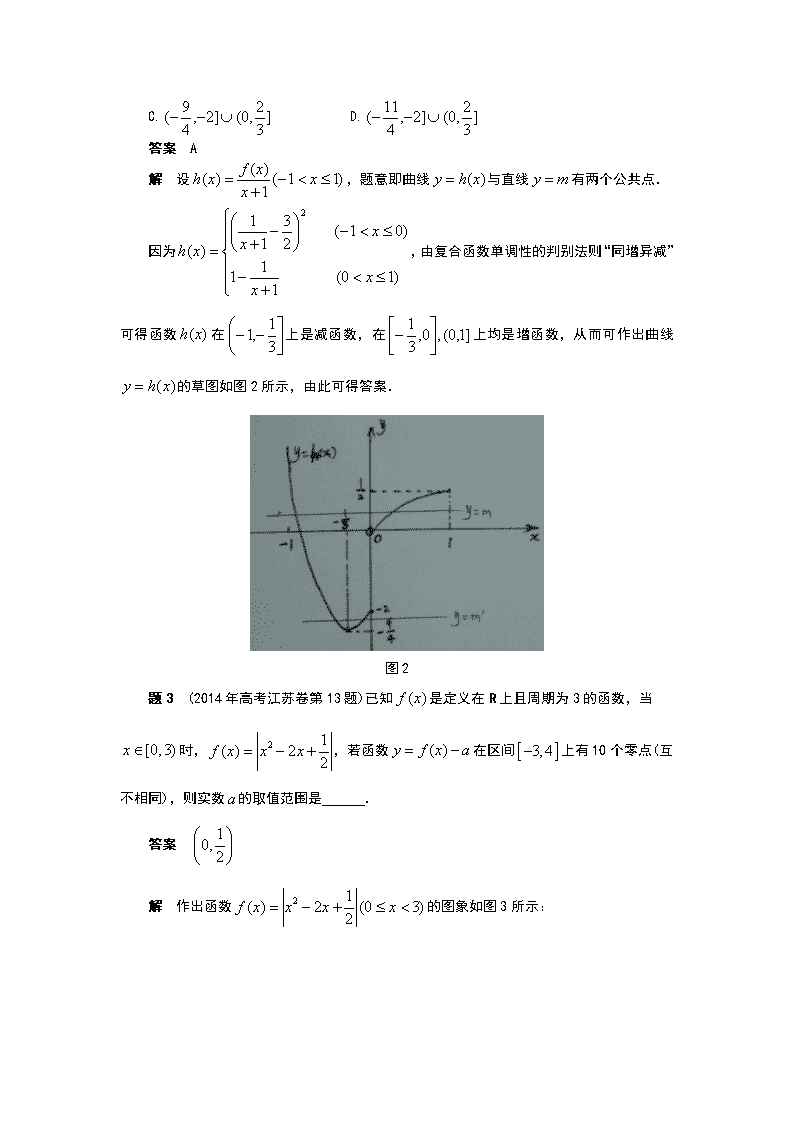
用分离常数法解2014年高考题 ‎1 用分离常数法讨论方程根的个数 题1 (2014年高考课标全国卷I理科第11题即文科第12题)已知函数，若存在唯一的零点，且，则的取值范围是( )‎ A. B. C. D.‎ 答案 C 解 因为函数的零点不为0，所以可得本题的题干等价于“关于的方程有唯一实根，且该实根是正数，求的取值范围”，也等价于“关于的方程有唯一实根，且该实根是正数，求的取值范围”．‎ 用导数容易作出曲线如图1所示：‎ 图1‎ 由图1可得答案C．‎ ‎ 题2 (2014年重庆卷文科第10题)已知函数，且在内有且仅有两个不同的零点，则实数的取值范围是( )‎ ‎ A. B. ‎ C. D.‎ 答案 A 解 设，题意即曲线与直线有两个公共点．‎ 因为，由复合函数单调性的判别法则“同增异减”可得函数在上是减函数，在上均是增函数，从而可作出曲线的草图如图2所示，由此可得答案．‎ 图2‎ 题3 (2014年高考江苏卷第13题)已知是定义在R上且周期为3的函数，当时，，若函数在区间上有10个零点(互不相同)，则实数的取值范围是 ．‎ 答案 ‎ 解 作出函数的图象如图3所示：‎ 图3‎ 有；当且仅当时，；．‎ 关于方程即在上有10个零点，即曲线与直线在上有10个交点．因为函数的周期为3，所以直线与曲线有4个交点，得所求实数的取值范围是．‎ 题4 (2014年高考天津卷理科第14题)已知函数f(x)＝|x2＋3x|，x∈R．若方程f(x)－a|x－1|＝0恰有4个互异的实数根，则实数a的取值范围为________．‎ 答案 (0,1)∪(9,＋∞)‎ 解 因为不是原方程的根，所以设后可得本题等价于：‎ 若关于的方程恰有4个互异的实根，则实数a的取值范围为________．‎ ‎ (1)作出对勾函数的图象如图4所示：‎ 图4‎ ‎ (2)再由平移可作出函数的图象如图5所示：‎ 图5‎ ‎ (3)作出函数的图象如图6所示：‎ 图6‎ 因为关于的方程的互异实根个数即两条曲线公共点的个数，所以由图6可得结论：‎ ‎①当时，原方程互异实根的个数是0；‎ ‎②当或时，原方程互异实根的个数是2；‎ ‎③当或9时，原方程互异实根的个数是3；‎ ‎④当或时，原方程互异实根的个数是4．‎ 所以本题的答案是(0,1)∪(9,＋∞)．‎ 题5 (2014年高考天津卷文科第14题)已知函数f(x)＝若函数y＝f(x)－a|x|恰有4个零点，则实数a的取值范围为________．‎ 答案 (1,2)‎ 简解 因为不是函数y＝f(x)－a|x|的零点，所以可得本题等价于：‎ 若两条曲线恰有4个公共点，则实数a的取值范围为________．‎ 同题4的解法，可作出曲线如图7所示：‎ 图7‎ 由图7可得结论：‎ ‎①当时，原方程互异实根的个数是0；‎ ‎②当或时，原方程互异实根的个数是3；‎ ‎③当时，原方程互异实根的个数是6；‎ ‎④当时，原方程互异实根的个数是5；‎ ‎⑤当时，原方程互异实根的个数是4．‎ 所以本题的答案是(1,2)．‎ 题6 (2014年高考天津卷理科第20(1)题)设f(x)＝x－aex(a∈R)，x∈R．已知函数y＝f(x)有两个零点x1，x2，且x10，讨论曲线公共点的个数． ‎ ‎ 2.(2013年高考新课标卷I理科第21题)已知函数．若曲线和曲线都过点，且在点处有相同的切线．‎ ‎(1)求的值；‎ ‎(2)若时，，求的取值范围．‎ ‎3.(2013年高考福建卷文科第22题)已知函数R，e为自然对数的底数)．‎ ‎(1)若曲线在点处的切线平行于轴，求的值；‎ ‎(2)求函数的极值；‎ ‎(3)当时，若直线与曲线没有公共点，求的最大值．‎ 答案：‎ ‎1.当时，有0个公共点；当 时，有1个公共点；当有2个公共点．‎ ‎2.(1)．‎ ‎(2)题设即恒成立．‎ 设，可得题设即恒成立．‎ 得，所以：‎ 当时，恒成立，是增函数，所以恒成立即．‎ 当时，可得，所以恒成立即．‎ 所以所求的取值范围是．‎ ‎3.(1)e．(2)略．‎ ‎(3)题意即方程也即无解，满足．‎ 当时，即方程无解．用导数可求得函数的值域是，所以，即．‎ 总之，的取值范围是，所以的最大值是1．‎