高考数学经典题题精选平面向量解答题精选 6页

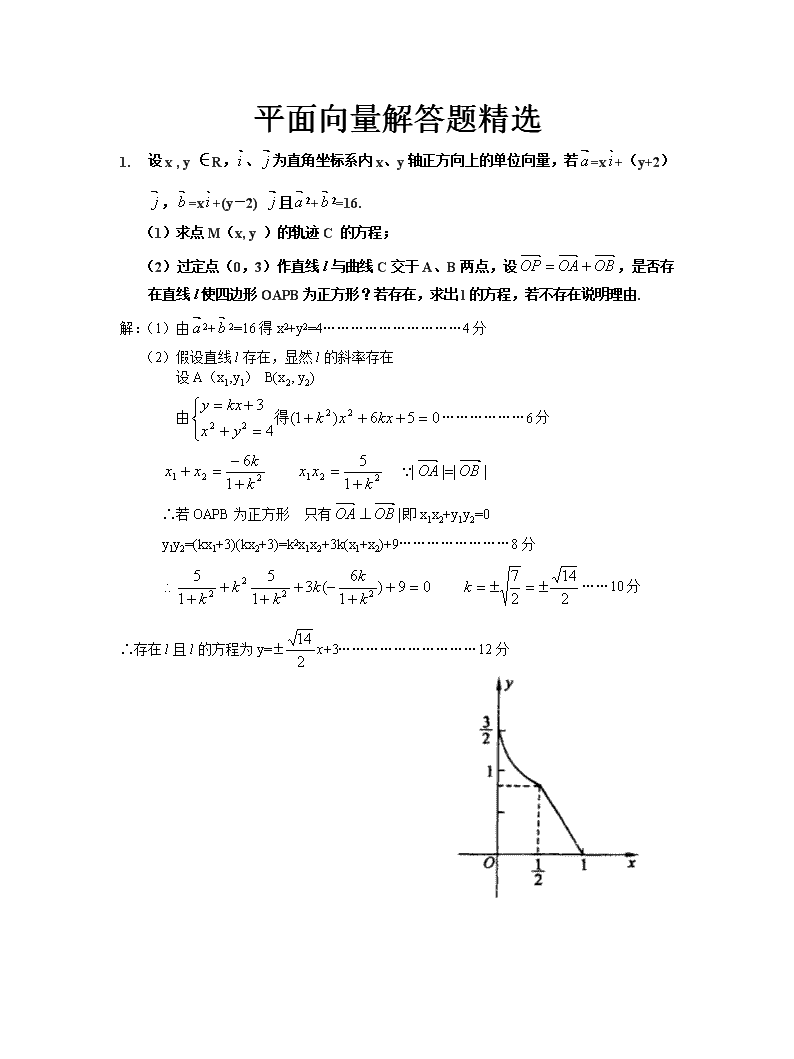
平面向量解答题精选 1. 设x , y ∈R，、为直角坐标系内x、y轴正方向上的单位向量，若=x+（y+2），=x+(y－2) 且2+2=16.‎ ‎ （1）求点M（x, y ）的轨迹C 的方程；‎ ‎ （2）过定点（0，3）作直线l与曲线C交于A、B两点，设，是否存在直线l使四边形OAPB为正方形？若存在，求出l的方程，若不存在说明理由.‎ 解：（1）由2+2=16得x2+y2=4…………………………4分 ‎ （2）假设直线l存在，显然l的斜率存在 ‎ 设A（x1,y1） B(x2, y2)‎ ‎ 由………………6分 ‎ ‎ ‎∴若OAPB为正方形 只有即x1x2+y1y2=0‎ y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9……………………8分 ‎……10分 ‎∴存在l且l的方程为y=x+3…………………………12分 1. ‎（1）已知||=4，||=3，（2－3）·（2+）=61，求与的夹角θ；‎ ‎ （2）设=（2，5），=（3，1），=（6，3），在上是否存在点M，使 ‎ ，若存在，求出点M的坐标，若不存在，请说明理由.‎ 解：（1）∵（2－3）·（2+）=61，∴…（12分）‎ ‎ 又||=4，||=3，∴·=－6.…………………………………………（4分）.‎ ‎ ………………………………………………（5分）‎ ‎ ∴θ=120°.………………………………………………………………（6分）‎ ‎ （2）设存在点M，且 ‎ ‎ ‎ …………………………（8分）‎ ‎ ‎ ‎∴存在M（2，1）或满足题意.……………………（12分）‎ 2. 设、是两个不共线的非零向量（）‎ ‎ （1）记那么当实数t为何值时，A、B、C三点共线？‎ ‎（2）若，那么实数x为何值时的值最小？‎ 解：（1）A、B、C三点共线知存在实数 ‎ 即，…………………………………………………4分 ‎ 则………………………………………………………………6分 ‎ （2）‎ ‎ ……………………………9分 ‎ 当…………………………………………12分 1. 设平面内的向量, , ，点P是直线OM上的一个动点，求当取最小值时，的坐标及ÐAPB的余弦值．‎ 解 设．‎ ‎∵ 点P在直线OM上，‎ ‎∴ 与共线，而，‎ ‎∴ x－2y=0即x=2y，有． ……………… 4分 ‎∵ ，，‎ ‎∴ ‎ ‎= 5y2－20y+12‎ ‎= 5(y－2)2－8． ……………… 8分 从而，当且仅当y=2，x=4时，取得最小值－8，此时，，．‎ 于是，，，‎ ‎∴ ．…………… 12分 2. 已知向量向量与向量夹角为，且.‎ ‎ （1）求向量；‎ ‎ （2）若向量与向量=（1，0）的夹角为，求|2+|的值.‎ 解：（1）设，有 ① ………………2分 由夹角为，有.‎ ‎∴②………………4分 由①②解得 ∴即或…………6分 ‎ （2）由垂直知…………7分 ‎…………10分 ‎∴…………12分 1. 已知定点 ‎（Ⅰ）求动点P的轨迹方程。‎ ‎（Ⅱ）当的最大值和最小值.‎ 解：（I）设动点的坐标为P(x,y),则 ‎（3分）‎ ‎ ‎ ‎ 若k=1，则方程为x=1，表示过点（1，0）是平行于y轴的直线.（4分）‎ ‎ 若k≠1，则方程化为：为半径的圆. （5分）‎ ‎ （II）当k=0时，方程化为x2+y2=1 .‎ ‎ ‎ 1. 在平行四边形ABCD中，A（1，1），，点M是线段AB的中点，线段CM与BD交于点P.‎ ‎ （1）若，求点C的坐标； （2）当时，求点P的轨迹.‎ 解：（1）设点C坐标为（……1分 ‎ 又……3分 ‎ 即……4分 即点C（0，6）…5分 ‎ （2）解一：设，则 ‎ ……6分 ‎……8分 ‎ ABCD为菱形……9分 ‎……11分 故点P的轨迹是以（5，1）为圆心，2为半圆去掉与直线的两个交点……12分 ‎ 解法二：‎ ‎ D的轨迹方程为……7分 M为AB中点 的比为 ‎ 设……9分 的轨迹方程 ‎ 整理得……11分 故点P的轨迹是以（5，1）为圆心，2为半径的圆去掉与直线的两个交点……12分 1. 已知向量=（2，2），向量与向量的夹角为，且·=－2，‎ ‎ （1）求向量；‎ ‎ （2）若，其中A、C是△ABC的内角，若三角形的三内角A、B、C依次成等差数列，试求|+|的取值范围.‎ 解：（1）设=（x,y），则 ‎∴解得 ‎ （2）. ∴‎ ‎∴‎ ‎=1+‎ ‎∴ ∴‎