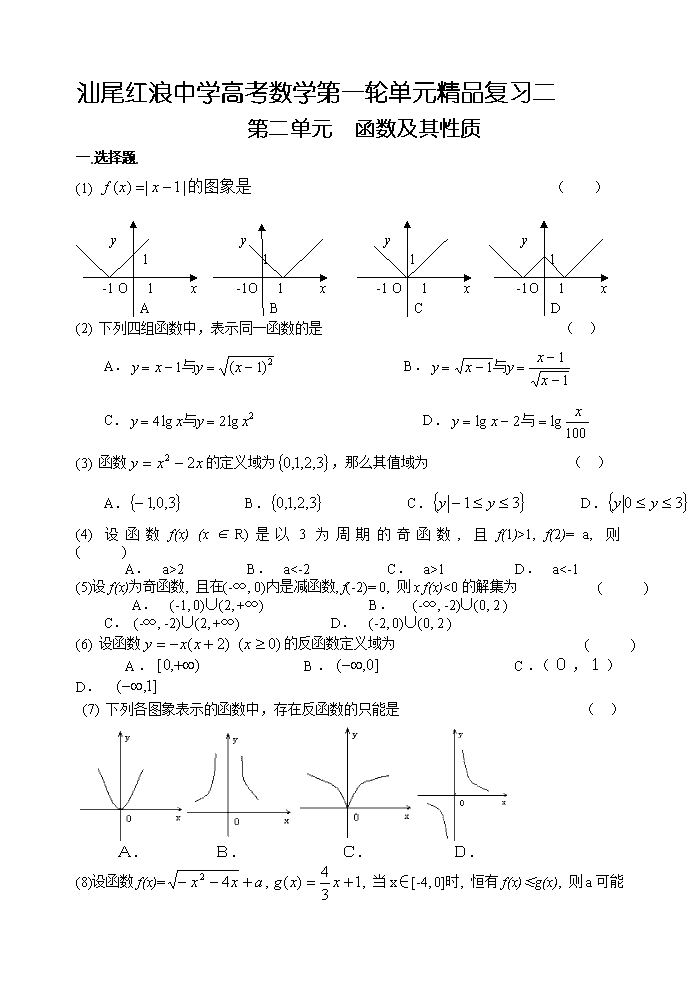汕尾红浪中学高考数学复习二 7页

汕尾红浪中学高考数学第一轮单元精品复习二 第二单元 函数及其性质 一.选择题.‎ A ‎1‎ x y O B ‎1‎ x y O C ‎1‎ x y O D ‎1‎ x y O ‎-1‎ ‎-1‎ ‎-1‎ ‎-1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎(1) （ ）‎ ‎(2) 下列四组函数中，表示同一函数的是　　　　　　　　　　　　　　　　　（　）‎ A． B．‎ C． D．‎ ‎(3) 函数的定义域为，那么其值域为　　　　　　　　　　（　）‎ A． B． C． D．‎ ‎(4) 设函数f(x) (x∈R)是以3为周期的奇函数, 且f(1)>1, f(2)= a, 则 　　　　　( )‎ ‎ A． a>2 B． a<‎-2 C． a>1 D． a<-1‎ ‎(5)设f(x)为奇函数, 且在(-∞, 0)内是减函数, f(-2)= 0, 则x f(x)<0的解集为 　　　 ( )‎ ‎ A． (-1, 0)∪(2, +∞) B． (-∞, -2)∪(0, 2 ) ‎ C． (-∞, -2)∪(2, +∞) D． (-2, 0)∪(0, 2 ) ‎ ‎(6) 设函数的反函数定义域为 　　　　　　　　　　　　　( )‎ ‎ A． B． C．（０，１） D． ‎ ‎ (7) 下列各图象表示的函数中，存在反函数的只能是　　　　　　　　　　　　　（　）‎ Ａ．　　　　　Ｂ．　　　　　　　Ｃ．　　　　　　Ｄ．　‎ ‎(8)设函数f(x)=, 当x∈[-4, 0]时, 恒有f(x)≤g(x), 则a 可能取的一个值是 　　　　　　　　　　　　　 ( )‎ ‎ A． -5 B． ‎5 C． - D． ‎ ‎　　　‎ ‎(9) 已知函数f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y), 且f(2)=4,则f(-1)= 　　　　( )‎ ‎ A． -2 B． ‎1 C． 0.5 D． 2‎ ‎(10) 已知，则下列不等式中成立的一个是　　　　　　　　　　　　　　（ ）‎ A． B． C． D．‎ 二.填空题 ‎(11) 奇函数定义域是，则 .‎ ‎(12) 若，则＿＿＿＿ ‎ ‎ (13) 函数在上的最大值与最小值之和为 .‎ ‎(14) 在R上为减函数，则 .‎ 三.解答题 ‎(15) 记函数的定义域为集合M，函数的定义域为集合N．求：‎ ‎（Ⅰ）集合M，N；‎ ‎（Ⅱ） 集合，‎ ‎(16) 设是奇函数，是偶函数，并且，求 ‎ ‎ ‎(17) 有一批材料可以建成长为的围墙，如果用材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的矩形（如图），则围成的矩形的最大面积是多少？‎ ‎(18) 已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).‎ ‎ (Ⅰ) 求函数f(x)的表达式；‎ ‎(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.‎ 参考答案 ‎ 一选择题:‎ ‎1.B ‎ ‎[解析]：=‎ ‎2.D ‎ ‎[解析]：∵=|x -1|∴A错 ‎ ∵的定义域是x1, 的定义域是x>1 ∴B错 ‎∵的定义域是x>0 ,的定义域是x0 ∴C错 ‎3.A ‎ ‎[解析]：只需把x=0，1，2，3代入计算y就可以了 ‎4.D ‎ ‎[解析]：‎ ‎5.C ‎ ‎[解析]：‎ ‎6.B ‎[解析]：函数的反函数定义域 就是原函数的值域 而 当时原函数是是减函数，故 ‎7. Ｄ ‎ ‎[解析]：根据反函数的定义，存在反函数的函数x、y是一一对应的。‎ ‎8. A ‎ ‎[解析]：排除法，‎ ‎ 若a=5,则x=0时f(x)=5，g(x)=1, 故A错 若a=,则x= - 4时f(x)= ，g(x)=, 故C错 若a=,则x=0时f(x)= ，g(x)=1, 故D错 ‎9.A ‎ ‎[解析]：因为函数f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y),所以 即 又 ‎ ‎ ‎10.D ‎ ‎[解析]：‎ 故 二填空题: ‎ ‎11. －１ ‎ ‎[解析]：∵是奇函数 ‎∴定义域关于原点对称 即 ∴‎ ‎12.－５ ‎ ‎[解析]：1 – 23= - 5‎ 13. ‎３ ‎ ‎[解析]：函数在上是增函数，所以最大值为2，最小值为1，它们之和为3‎ ‎14.‎ ‎[解析]：∵在R上为减函数 ∴‎ 三解答题 ‎(15)解：（Ⅰ）‎ ‎ ‎ ‎（Ⅱ）‎ ‎ .‎ ‎(16) 为奇函数 为偶函数 ‎ 从而 ‎ ‎（17）设每个小矩形长为x，宽为y，则 ‎(1８) (Ⅰ)由已知,设f1(x)=ax2,由f1(1)=1,得a=1, ∴f1(x)= x2.设f2(x)=(k>0),它的图象与直线y=x的交点分别为A(,)，B(－,－)‎ 由=8,得k=8,. ∴f2(x)=.故f(x)=x2+.‎ ‎(Ⅱ) （证法一）f(x)=f(a),得x2+=a2+, ‎ 即=－x2+a2+.在同一坐标系内作出f2(x)=和 f3(x)= －x2+a2+的大致图象,其中f2(x)的图象是以坐 标轴为渐近线,且位于第一、三象限的双曲线, f3(x)与的图象是以(0, a2+)为顶点,开口向下的抛物线.因此, f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.又∵f2(2)=4, f3(2)= －4+a2+，当a>3时,. f3(2)－f2(2)= a2+－8>0,当a>3时,在第一象限f3(x)的图象上存在一点(2,f(2))在f2(x)图象的上方.f2(x)与f3(x)的图象在第一象限有两个交点,即f(x)=f(a)有两个正数解.因此,方程f(x)=f(a)有三个实数解.‎ ‎（证法二）由f(x)=f(a),得x2+=a2+,即(x－a)(x+a－)=0,得方程的一个解x1=a.方程x+a－=0化为ax2+a2x－8=0,由a>3,△=a4+‎32a>0,得x2=, x3=‎ ‎,x2<0, x3>0, ∵x1≠ x2,且x2≠ x3.若x1= x3,即a=,则‎3a2=, a4=‎4a,得a=0或a=,这与a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三个实数解.‎