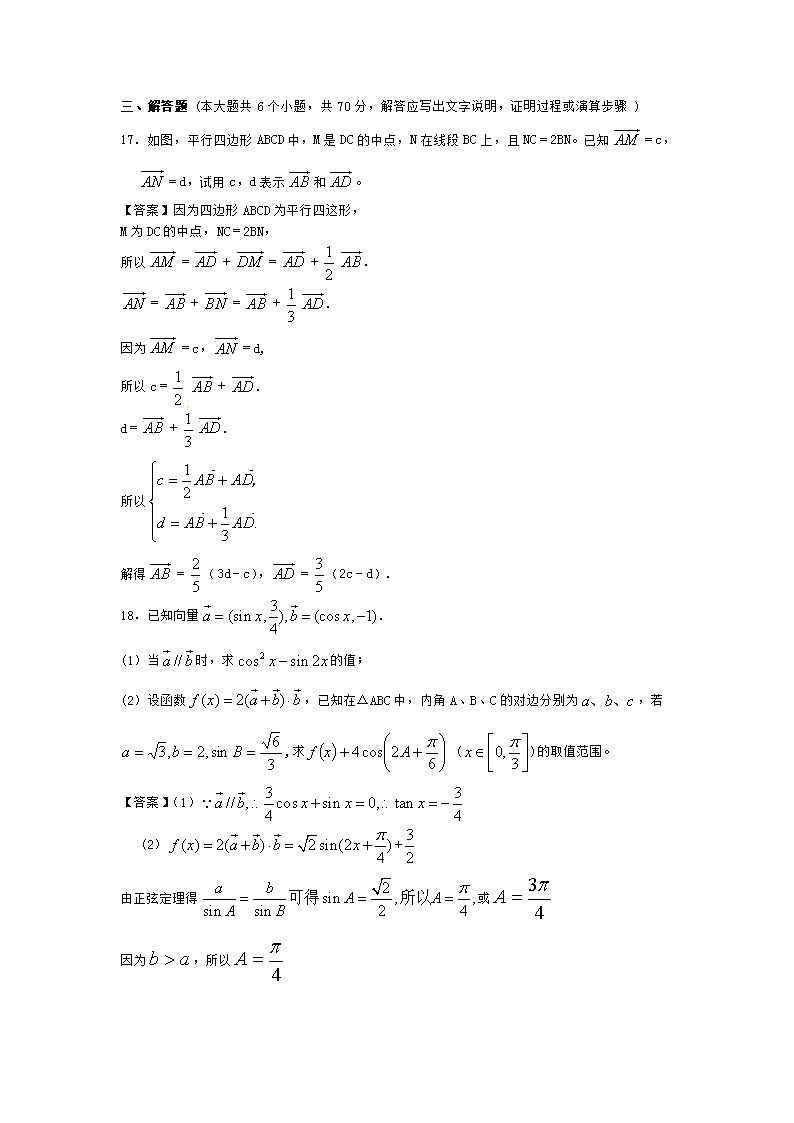天津工业大学附中高考数学一轮复习单元精品训练平面向量 5页

天津工业大学附中2019届高考数学一轮复习单元精品训练：平面向量 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．‎ 第Ⅰ卷(选择题　共60分)‎ 一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．若，．，且，则向量与的夹角为( )‎ A．300 B．600 C．1200 D．1500‎ ‎【答案】C ‎2．设=（1,-2），=（a,-1），=（-b，0），a>0,b>0,O为坐标原点，若A、B、C三点共线，则的最小值是( )‎ A．2 B．4 C．6 D．8‎ ‎【答案】D ‎3．已知向量，,,则( )‎ A． B． C． 5 D． 25‎ ‎【答案】C ‎4．设非零向量a，b，c，若，那么|p|的取值范围为( )‎ A．[0,1] B．[0,2] C．[0,3] D．[1,2]‎ ‎【答案】C ‎5．已知向量，，则向量与的夹角为( )‎ A． B． C． D．‎ ‎【答案】A ‎6．已知，若对任意则( )‎ A．=90° B．=90° ‎ C．=90° D．===60°‎ ‎【答案】C ‎7．如图，设P、Q为△ABC内的两点，且， ＝＋，则△ABP的面积与△ABQ的面积之比为( )‎ ‎[来源:学|科|网Z|X|X|K]‎ A． B． C． D．‎ ‎【答案】B[来源:1]‎ ‎8．如图，半圆的直径AB=6，O为圆心，C为半圆上不同于 A．B的任意一点，若P为半径OC上的动点， 则的最小值是( )‎ A． B． C． D． ‎ ‎【答案】A ‎9．点M是边长为2的正方形ABCD内或边界上一动点，N是边BC的中点，则的最大值是( )‎ A．2 B．4 C．5 D．6‎ ‎【答案】D ‎10．下面给出四种说法，其中正确的个数是( )‎ ‎①对于实数m和向量a、b，恒有m(a-b)=ma-mb；②对于实数m、n和向量a，恒有(m-n)a=ma-na；‎ ‎③若ma=mb(m∈R)，则a=b；④若ma=na(a≠0)，则m=n.‎ A．1 B．2 C．3 D．4‎ ‎【答案】C ‎11．已知向量,向量则的最大值，最小值分别是( )‎ A． B． C．16，0 D．4，0‎ ‎【答案】D ‎12．若向量，，且与共线，则实数的值为( )‎ A． B． C． D．‎ ‎【答案】D 第Ⅱ卷(非选择题　共90分)‎ 二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)‎ ‎13．已知的夹角为，以为邻边作平行四边形，则此平行四边形的两条对角线中较长的一条的长度为____________‎ ‎【答案】‎ ‎14．若向量的夹角为，，则 .[来源:学|科|网Z|X|X|K]‎ ‎【答案】2‎ ‎15．已知是单位向量，，则在方向上的投影为 。‎ ‎【答案】‎ ‎16．在中，，，是边的中点，则      ．‎ ‎【答案】 ‎ 三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17．如图，平行四边形ABCD中，M是DC的中点，N在线段BC上，且NC＝2BN。已知＝c，＝d，试用c，d表示和。‎ ‎【答案】因为四边形ABCD为平行四这形，‎ M为DC的中点，NC＝2BN，‎ 所以＝＋＝＋. ‎ ‎＝＋＝＋.[来源:Zxxk.Com]‎ 因为＝c，＝d,‎ 所以c＝＋.‎ d＝＋.‎ 所以 ‎ 解得＝（3d－c），＝（2c－d）. ‎ ‎18．已知向量.‎ ‎(1）当时，求的值；‎ ‎(2）设函数，已知在△ABC中，内角A、B、C的对边分别为，若,求 ()的取值范围。‎ ‎【答案】（1）‎ ‎ (2）+‎ 由正弦定理得或 ‎ 因为，所以 ‎ 所以 ‎ ‎19．已知单位向量的夹角为求向量的夹角。‎ ‎【答案】有单位向量的夹角为，得 又 3‎ 所以,设的夹角为,‎ ‎ 又所以。‎ 即向量与的夹角为。‎ ‎20．已知锐角中，三个内角为，向量，‎ ‎，‖,求的大小．‎ ‎【答案】，‎ 又‖‎ 又为锐角，则 ‎ ‎21．已知向量 ‎ ‎ (1)当向量与向量共线时，求的值；‎ ‎ (2)求函数的最大值,并求函数取得最大值时的的值.‎ ‎【答案】(1)共线,∴,∴.‎ ‎(2),‎ ‎，函数的最大值为,得函数取得最大值时 ‎ ‎22．如图，函数y=2sin(πx＋φ),x∈R,(其中0≤φ≤)的图象与y轴交于点（0，1）。(Ⅰ)求φ的值；(Ⅱ)若，求函数y=2sin(πx＋φ)的最值，及取得最值时的值；(Ⅲ)设P是图象上的最高点，M、N是图象与x轴的交点，求的余弦值。‎ ‎[来源:学+科+网Z+X+X+K]‎ ‎【答案】（1）由已知，又 ‎(2）‎ ‎(3）设的夹角为 由已知 ‎