高考数学教师备选作业立体几何体中的向量方法理 8页

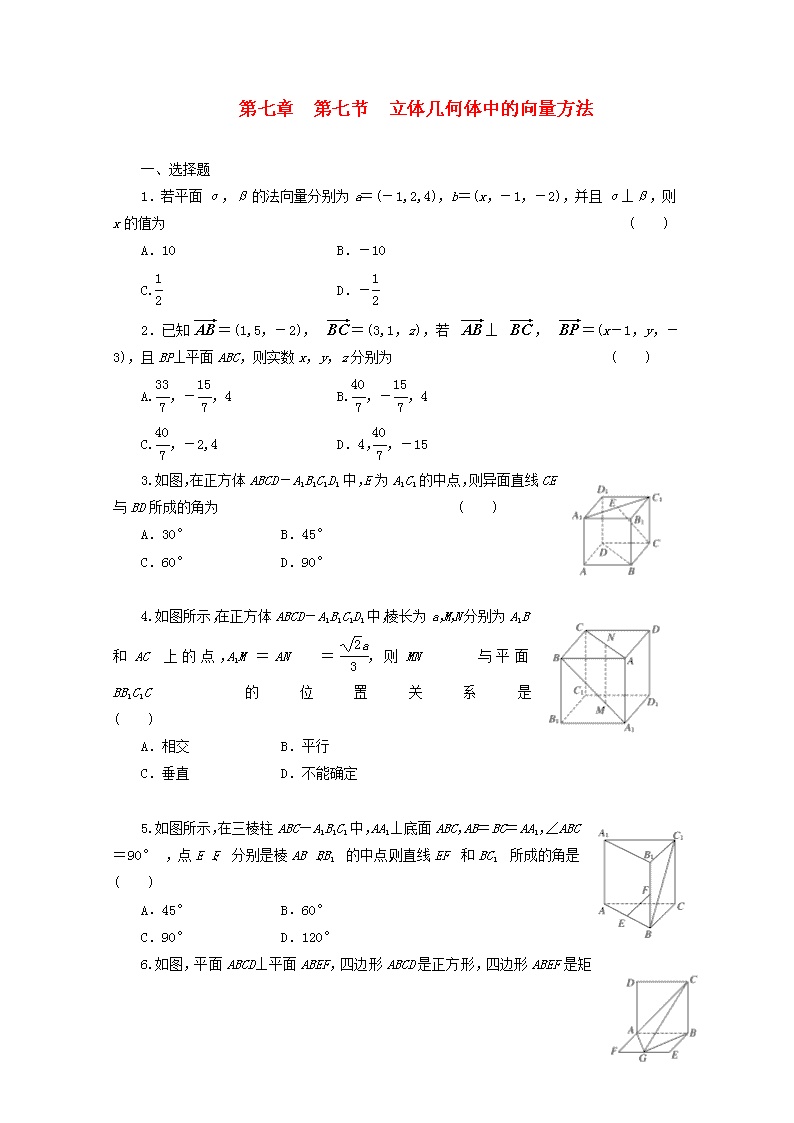
第七章 第七节 立体几何体中的向量方法 一、选择题 ‎1．若平面α，β的法向量分别为a＝(－1,2,4)，b＝(x，－1，－2)，并且α⊥β，则x的值为 (　　)‎ A．10　　　　　　　　　　 B．－10‎ C. D．－ ‎2．已知＝(1,5，－2)， ＝(3,1，z)，若 ⊥ ， ＝(x－1，y，－3)，且BP⊥平面ABC，则实数x，y，z分别为 (　　)‎ A.，－，4 B.，－，4‎ C.，－2,4 D．4，，－15‎ ‎3.如图，在正方体ABCD－A1B‎1C1D1中，E为A‎1C1的中点，则异面直线CE与BD所成的角为 (　　)‎ A．30° B．45°‎ C．60° D．90°‎ ‎4.如图所示，在正方体ABCD－A1B‎1C1D1中，棱长为a，M，N分别为A1B和AC上的点，A‎1M＝AN＝，则MN与平面BB‎1C1C的位置关系是 (　　)‎ A．相交 B．平行 C．垂直 D．不能确定 ‎5.如图所示，在三棱柱ABC—A1B‎1C1中，AA1⊥底面ABC，AB＝BC＝AA1，∠ABC＝90°，点E、F分别是棱AB、BB1的中点，则直线EF和BC1所成的角是 (　　)‎ A．45° B．60°‎ C．90° D．120°‎ ‎6.如图，平面ABCD⊥平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，且AF＝AD＝a，G是EF的中点，则GB与平面AGC所成角的正弦值为 (　　)‎ A. B. C. D. 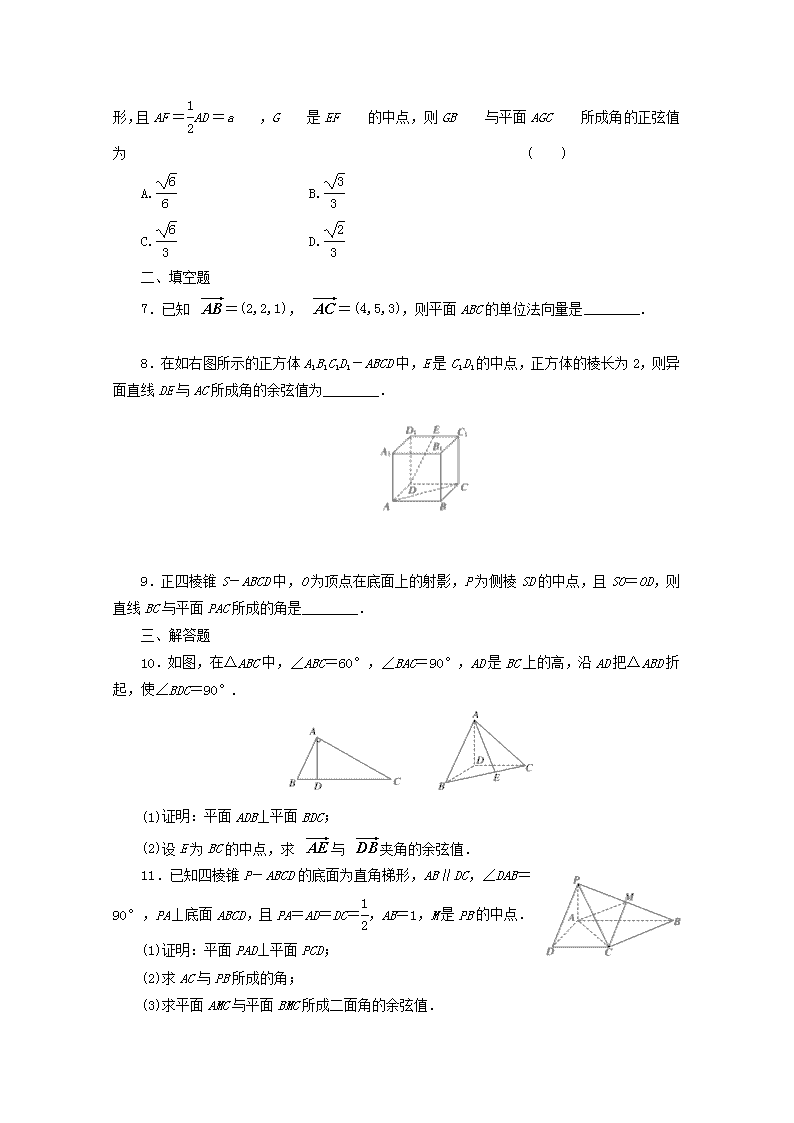二、填空题 ‎7．已知 ＝(2,2,1)， ＝(4,5,3)，则平面ABC的单位法向量是________．‎ ‎8．在如右图所示的正方体A1B‎1C1D1－ABCD中，E是C1D1的中点，正方体的棱长为2，则异面直线DE与AC所成角的余弦值为________．‎ ‎9．正四棱锥S－ABCD中，O为顶点在底面上的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面PAC所成的角是________．‎ 三、解答题 ‎10．如图，在△ABC中，∠ABC＝60°，∠BAC＝90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC＝90°.‎ ‎(1)证明：平面ADB⊥平面BDC；‎ ‎(2)设E为BC的中点，求 与 夹角的余弦值．‎ ‎11．已知四棱锥P－ABCD的底面为直角梯形，AB∥DC，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝，AB＝1，M是PB的中点．‎ ‎(1)证明：平面PAD⊥平面PCD；‎ ‎(2)求AC与PB所成的角；‎ ‎(3)求平面AMC与平面BMC所成二面角的余弦值．‎ ‎12．如图，四棱锥P－ABCD中，PA⊥底面ABCD.四边形ABCD中，AB⊥AD，AB＋AD＝4，CD＝，∠CDA＝45°.‎ ‎(1)求证：平面PAB⊥平面PAD；‎ ‎(2)设AB＝AP.‎ ‎(ⅰ)若直线PB与平面PCD所成的角为30°，求线段AB的长；‎ ‎(ⅱ)在线段AD上是否存在一个点G，使得点G到点P、B、C、D的距离都相等？说明理由．‎ 详解答案 一、选择题 ‎1．解析：∵α⊥β，∴a·b＝0‎ ‎∴x＝－10.‎ 答案：B ‎2．解析： ⊥ ⇒ · ＝3＋5－2z＝0，∴z＝4.‎ 又BP⊥平面ABC，‎ ‎∴·＝x－1＋5y＋6＝0，①‎ ‎·＝3x－3＋y－3z＝0，②‎ 由①②得x＝，y＝－.‎ 答案：B ‎3. 解析：以D点为原点，建立空间直角坐标系，‎ 设正方体棱长为1，则相关点的坐标为C(0,1,0)，E(，，1)，B(1,1,0)，D(0,0,0)，∴ ＝(，－，1)， ＝(－1，－1,0)．‎ ‎∴ · ＝－＋＋0＝0.‎ ‎∴ ⊥ ，即CE⊥BD.‎ 答案：D ‎4. 解析：分别以C1B1，C1D1，C‎1C所在直线为x，y，z轴，建立空间直角坐标系．‎ ‎∵A‎1M＝AN＝a，‎ ‎∴M(a，a，)，N(a，a，a)．‎ ‎∴ ＝(－，0，a)．‎ 又C1 (0,0,0)，D1(0，a,0)，‎ ‎∴ ＝(0，a,0)．‎ ‎∴ · ＝0，∴⊥ .‎ ‎∵ 是平面BB‎1C1C的法向量，‎ 且MN⊄平面BB‎1C1C，‎ ‎∴MN∥平面BB‎1C1C.‎ 答案：B ‎5. 解析：以B点为坐标原点，以BC、BA、BB1分别为x、y、z轴建立空间直角坐标系．设AB＝BC＝AA1＝2，‎ 则B(0,0,0)，C1(2,0,2)，E(0,1,0)，F(0,0，1)，‎ ‎∴ ＝(0，－1,1)， ＝(2,0,2)‎ ‎∴cos〈 ， 〉＝ ‎＝＝.∴EF与BC1所成角为60°.‎ 答案：B ‎6. 解析：如图，以A为原点建立空间直角坐标系，‎ 则A(0,0,0)，B(0,‎2a,0)，C(0,‎2a,‎2a)，G(a，a,0)，F(a,0,0)， ＝(a，a,0)， ＝(0,‎2a,‎2a)，‎ ‎＝(a，－a,0)， ＝(0,0,‎2a)，‎ 设平面AGC的法向量为n1＝(x1，y1,1)，‎ 由⇒⇒⇒‎ n1＝(1，－1,1)．‎ sinθ＝＝＝.‎ 答案：C 二、填空题 ‎7．解析：设平面ABC的法向量n＝(x，y,1)，‎ 则n⊥ 且n⊥ ，‎ 即n· ＝0，且n·＝0.‎ 即即 ‎∴n＝(，－1,1)，单位法向量为 ‎±＝±(，－，)．‎ 答案：(，－，)或(－，，－)‎ ‎8．解析：分别以DA，DC，DD1为x，y，z轴建立空间直角坐标系，则C(0,2,0)，E(0,1,2)，A(2,0,0)，‎ ‎＝(－2,2,0)， ＝(0,1,2)，‎ ‎∴cos〈 ， 〉＝.‎ 答案： ‎9．解析：如图，以O为原点建立空间直角坐标系O－xyz.设OD＝SO＝OA＝OB＝OC＝a，‎ 则A(a,0,0)，B(0，a,0)，‎ C(－a,0,0)，P(0，－，)，‎ 则 ＝(‎2a,0,0) ＝(－a，－，)， ＝(a，a,0)，‎ 设平面PAC的法向量为n，可求得n＝(0,1,1)，‎ 则cos〈 ，n〉＝＝＝，‎ ‎∴〈 ，n〉＝60°.∴直线BC与平面PAC所成的角为90°－60°＝30°.‎ 答案：30°‎ 三、解答题 ‎10．解：(1)证明：∵折起前AD是BC边上的高，‎ ‎∴当△ABD折起后，AD⊥DC，AD⊥DB.‎ 又DB∩DC＝D，‎ ‎∴AD⊥平面BDC.‎ ‎∵AD⊂平面ABD，‎ ‎∴平面ABD⊥平面BDC.‎ ‎(2)由∠BDC＝90°及(1)知DA，DB，DC两两垂直，不妨设|DB|＝1，以D为坐标原点，以 ， ， 所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系，易得D(0,0,0)，B(1,0,0)，C(0,3,0)，A(0,0，)，E(，，0)，‎ ‎∴ ＝(，，－)， ＝(1,0,0)，‎ ‎∴ 与 夹角的余弦值为 cos〈，〉＝＝＝.‎ ‎11．解：以A为坐标原点，AD长为单位长度，如图建立空间直角坐标系，则各点坐标为A(0,0,0)，B(0,2,0)，C(1,1,0)，D(1,0,0)，P(0,0,1)，M(0,1，)．‎ ‎(1)证明：因 ＝(0,0,1)， ＝(0,1,0)，故 · ＝0，所以AP⊥DC.‎ 由题设知AD⊥DC，且AP与AD是平面PAD内的两条相交直线，由此得DC⊥平面PAD.‎ 又DC在平面PCD上，故面PAD⊥面PCD.‎ ‎(2)因 ＝(1,1,0)， ＝(0,2，－1)，‎ 故| |＝，| |＝， · ＝2，‎ 所以cos< ， >＝＝.‎ ‎(3)在MC上取一点N(x，y，z)，则存在λ∈R，使 ＝λ ，‎ ‎＝(1－x,1－y，－z)， ＝(1,0，－)，‎ ‎∴x＝1－λ，y＝1，z＝λ.‎ 要使AN⊥MC，只需 · ＝0即x－z＝0，‎ 解得λ＝.‎ 可知当λ＝时，N点坐标为(，1，)，‎ 能使 · ＝0.‎ 此时，＝(，1，)， ＝(，－1，)，‎ 有 · ＝0‎ 由 · ＝0， · ＝0得AN⊥MC，BN⊥MC.‎ 所以∠ANB为所求二面角的平面角．‎ ‎∵| |＝，| |＝， · ＝－.‎ ‎∴cos〈， 〉＝＝－.‎ ‎∴平面AMC与平面BMC所成角的余弦值为－.‎ ‎12．解：(1)证明：因为PA⊥平面ABCD，‎ AB⊂平面ABCD，‎ 所以PA⊥AB.‎ 又AB⊥AD，PA∩AD＝A，‎ 所以AB⊥平面PAD.‎ 又AB⊂平面PAB，所以平面PAB⊥平面PAD.‎ ‎(2)以A为坐标原点，建立空间直角坐标系A－xyz(如图)．‎ 在平面ABCD内，作CE∥AB交AD于点E，‎ 则CE⊥AD.‎ 在Rt△CDE中，DE＝CD·cos 45°＝1，‎ CE＝CD·sin 45°＝1.‎ 设AB＝AP＝t，则B(t,0,0)，P(0,0，t)．‎ 由AB＋AD＝4得AD＝4－t，‎ 所以E(0,3－t,0)，C(1,3－t,0)，D(0,4－t,0)，‎ ‎＝(－1,1,0)， ＝(0,4－t，－t)．‎ ‎(ⅰ)设平面PCD的一个法向量为n＝(x，y，z)，‎ 由n⊥ ，n⊥ ，得 取x＝t，得平面PCD的一个法向量n＝(t，t,4－t)．‎ 又 ＝(t,0，－t)，‎ 故由直线PB与平面PCD所成的角为30°得 cos 60°＝||，‎ 即＝，‎ 解得t＝或t＝4(舍去，因为AD＝4－t＞0)，‎ 所以AB＝.‎ ‎(ⅱ)假设在线段AD上存在一个点G，使得点G到P，B，C，D的距离都相等，‎ 设G(0，m,0)(其中0≤m≤4－t)，‎ 则 ＝(1,3－t－m,0)，‎ ‎＝(0,4－t－m,0)，‎ ‎＝(0，－m，t)．‎ 由| |＝| |得 ‎12＋(3－t－m)2‎ ‎＝(4－t－m)2，‎ 即t＝3－m；(1)‎ 由| |＝| |得(4－t－m)2＝m2＋t2.(2)‎ 由(1)、(2)消去t，化简得m2－‎3m＋4＝0.(3)‎ 由于方程(3)没有实数根，所以在线段AD上不存在一个点G，使得点G到点P、C、D的距离都相等．从而，在线段AD上不存在一个点G，使得点G到点P、B、C、D的距离都相等．‎