广东高考数学理科数列真题含答案 13页

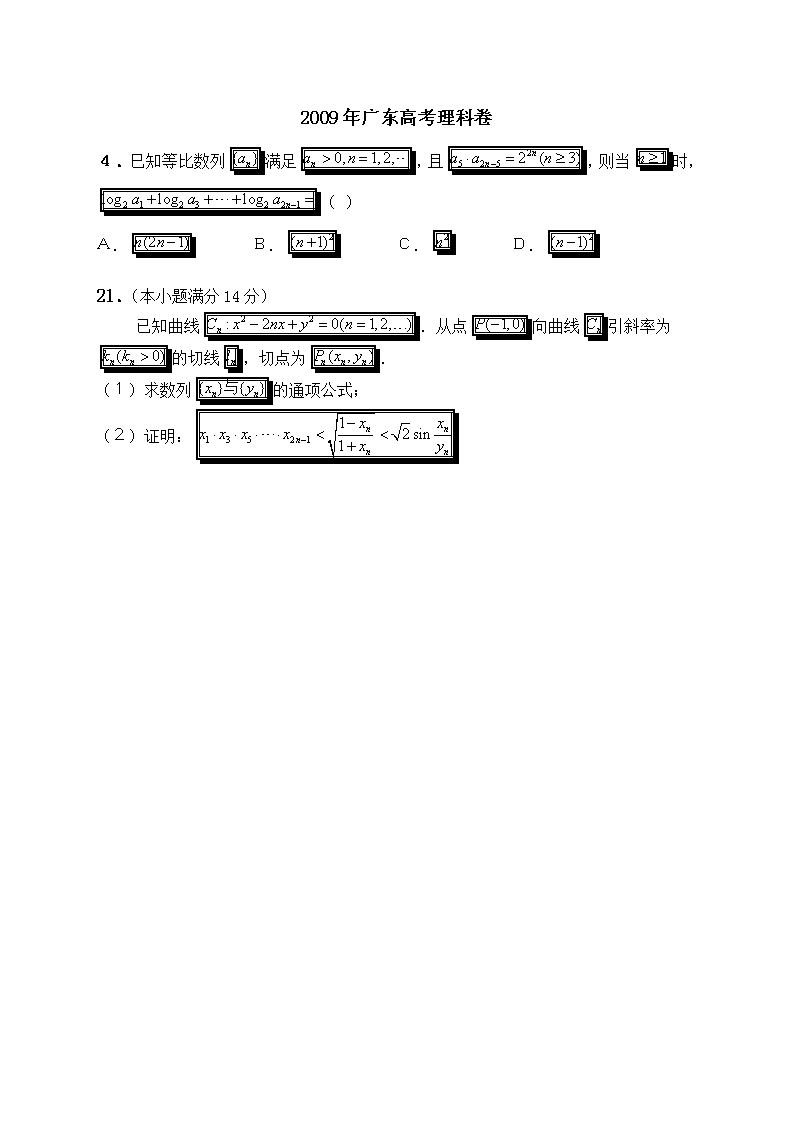
‎2007年广东高考理科卷 ‎5.已知数列{an}的前n项和，第k项满足,则 A. 9 B. ‎8 C. 7 D. 6‎ ‎21.（本小题满分14分）‎ 已知函数是方程的两个根,是的导数.设,‎ ‎(1)求的值；‎ ‎(2)证明：对任意的正整数n，都有;‎ ‎(3)记,求数列的前n项和.‎ ‎2008年广东高考理科卷 ‎2．记等差数列的前项和为，若，，则（ ）‎ A．16 B．‎24 ‎ C．36 D．48‎ ‎21．（本小题满分12分）‎ 设为实数，是方程的两个实根，数列满足，，（…）．‎ ‎（1）证明：，；‎ ‎（2）求数列的通项公式；‎ ‎（3）若，，求的前项和．‎ ‎2009年广东高考理科卷 ‎４．巳知等比数列满足，且，则当时，（ ）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎21．（本小题满分14分）‎ 已知曲线．从点向曲线引斜率为的切线，切点为．‎ ‎（１）求数列的通项公式；‎ ‎（２）证明：‎ ‎2010年广东高考理科卷 ‎4.已知为等比数列,是它的前项和.若, 且与的等差中项为,则w_w w.k*s_5 u.c o_m A. B. C. D.‎ ‎2011年广东高考理科卷 ‎11. 等差数列前9项的和等于前4项的和. 若，则k=____________.‎ ‎20.（本小题共14分）‎ 设b>0,数列满足a1=b，.‎ ‎（1）求数列的通项公式；‎ ‎（2）证明：对于一切正整数n，‎ ‎2012年广东高考理科卷 ‎11.已知递增的等差数列满足，则_____________‎ ‎19. （本小题满分14分）‎ 设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1，n∈N﹡,且a1，a2+5，a3成等差数列。‎ 求a1的值；‎ 求数列{an}的通项公式。‎ 证明：对一切正整数n，有.‎ 答案解析 ‎2007年广东高考理科卷 ‎5. 答案为：B 解析:由，可根据.‎ 解得.‎ 再根据5＜2k－10＜8,解得7.5＜k＜9,∴k=8.‎ ‎21.解:(1) 由 得 ‎ ‎ ‎ ‎(2)(数学归纳法)①当时,命题成立;‎ ‎②假设当时命题成立,即 ‎,又等号成立时时,时命题成立;‎ 由①②知对任意均有.‎ ‎ (3) ‎ ‎ ‎ ‎ 同理 ‎ ‎ 又 ‎ ‎ 数列是一个首项为 ,公比为2的等比数列;‎ ‎ .‎ ‎2008年广东高考理科卷 ‎2．答案为： D ‎【解析】，，故 ‎21．解：（1）由求根公式，不妨设，得 ‎，‎ ‎（2）设，则，由 得，，消去，得，是方程的根，‎ 由题意可知，‎ ‎①当时，此时方程组的解记为 即、分别是公比为、的等比数列，‎ 由等比数列性质可得,,‎ 两式相减，得 ‎，，‎ ‎，‎ ‎，即，‎ ‎②当时，即方程有重根，，‎ 即，得，不妨设，由①可知 ‎，，‎ 即，等式两边同时除以，得，即 数列是以1为公差的等差数列，‎ ‎，综上所述，‎ ‎（3）把，代入，得，解得 ‎，‎ ‎.‎ ‎2009年广东高考理科卷 ‎4. 答案为： C 解：在中，令n=5,得，令n=3,得 ‎，又，所以，，‎ 从而解得，公比，，，，‎ 所以1+3+…+（2n-1）=‎ ‎21.（1）解：曲线可化为，‎ 所以，它表示以为圆心，以n 为半径的圆，切线的方程为，‎ 联立，消去y 整理，得，①‎ ‎，‎ 令，解得， ‎ 此时，方程①化为 整理，得，解得，‎ 所以 ，‎ ‎∴数列的通项公式为，数列的通项公式为。‎ ‎（２）证明：∵，‎ ‎ ==， ∵=，又 令，则，要证明，‎ 只需证明当时，恒成立即可。‎ 设函数，‎ ‎ 则，‎ ‎∵ 在区间上为增函数，‎ ‎∴当时，，‎ ‎∴在区间上为单调递减函数，‎ ‎∴ 对于一切很成立， ‎ ‎∴ ，即=‎ 综上，得 ‎2010年广东高考理科卷 ‎4.答案为：C　‎ ‎∵数列为等比数列，∴，∴＝2.‎ 又∵与2的等差中项为，即有，∴.‎ ‎∴.∴＝，.∴. ‎ ‎2011年广东高考理科卷 ‎11.答案为 10.‎ 由题意可知， ，所以，则，‎ ‎20．解（１）法一：，得，‎ 设，则，‎ ‎（ⅰ）当时，是以为首项，为公差的等差数列，‎ 即，∴‎ ‎（ⅱ）当时，设，则，‎ 令，得，，‎ 知是等比数列，，又，‎ ‎，．‎ 法二：（ⅰ）当时，是以为首项，为公差的等差数列，‎ 即，∴‎ ‎（ⅱ）当时，，，，‎ 猜想，下面用数学归纳法证明：‎ ‎①当时，猜想显然成立；‎ ‎②假设当时，，则 ‎，‎ 所以当时，猜想成立，‎ 由①②知，，．‎ ‎（２）（ⅰ）当时， ，故时，命题成立；‎ ‎（ⅱ）当时，，‎ ‎，‎ ‎，以上n个式子相加得 ‎，‎ ‎．故当时，命题成立；‎ 综上（ⅰ）（ⅱ）知命题成立．‎ ‎2012年广东高考理科卷 ‎11.答案为 .‎ 解析：在递增的等差数列满足，则 解得，.‎ ‎19.（1）在中 ‎ 令得：‎ ‎ 令得：‎ 解得：，‎ 又，解得 ‎（2）由，得 ‎，又也满足 所以成立，∴ ‎ ‎∴ ，∴ ‎ ‎（3）（法一）∵‎ ‎∴ ∴，‎