高考数学理几何证明选讲二轮提高练习题目 11页

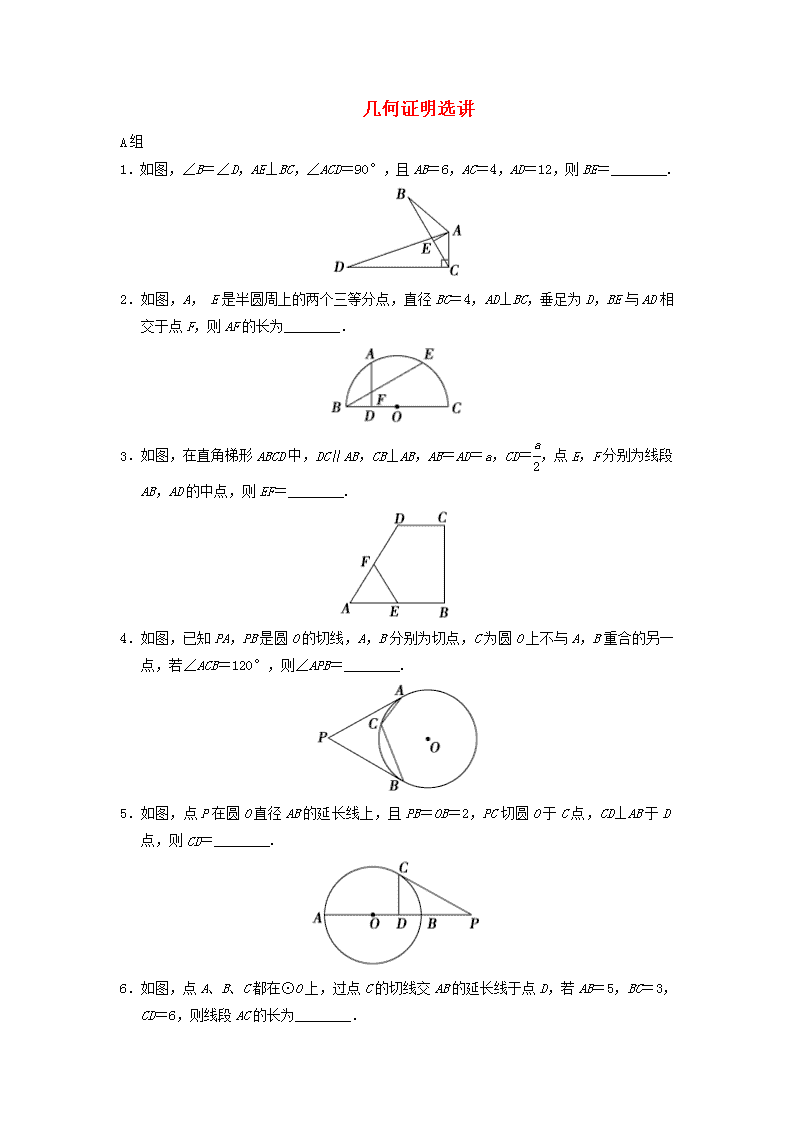
‎　几何证明选讲 A组 ‎1．如图，∠B＝∠D，AE⊥BC，∠ACD＝90°，且AB＝6，AC＝4，AD＝12，则BE＝________.‎ ‎2．如图，A， E是半圆周上的两个三等分点，直径BC＝4，AD⊥BC，垂足为D，BE与AD相交于点F，则AF的长为________．‎ ‎3．如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝，点E，F分别为线段AB，AD的中点，则EF＝________.‎ ‎4．如图，已知PA，PB是圆O的切线，A，B分别为切点，C为圆O上不与A，B重合的另一点，若∠ACB＝120°，则∠APB＝________.‎ ‎5．如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD⊥AB于D点，则CD＝________.‎ ‎6．如图，点A、B、C都在⊙O上，过点C的切线交AB的延长线于点D，若AB＝5，BC＝3，CD＝6，则线段AC的长为________．‎ ‎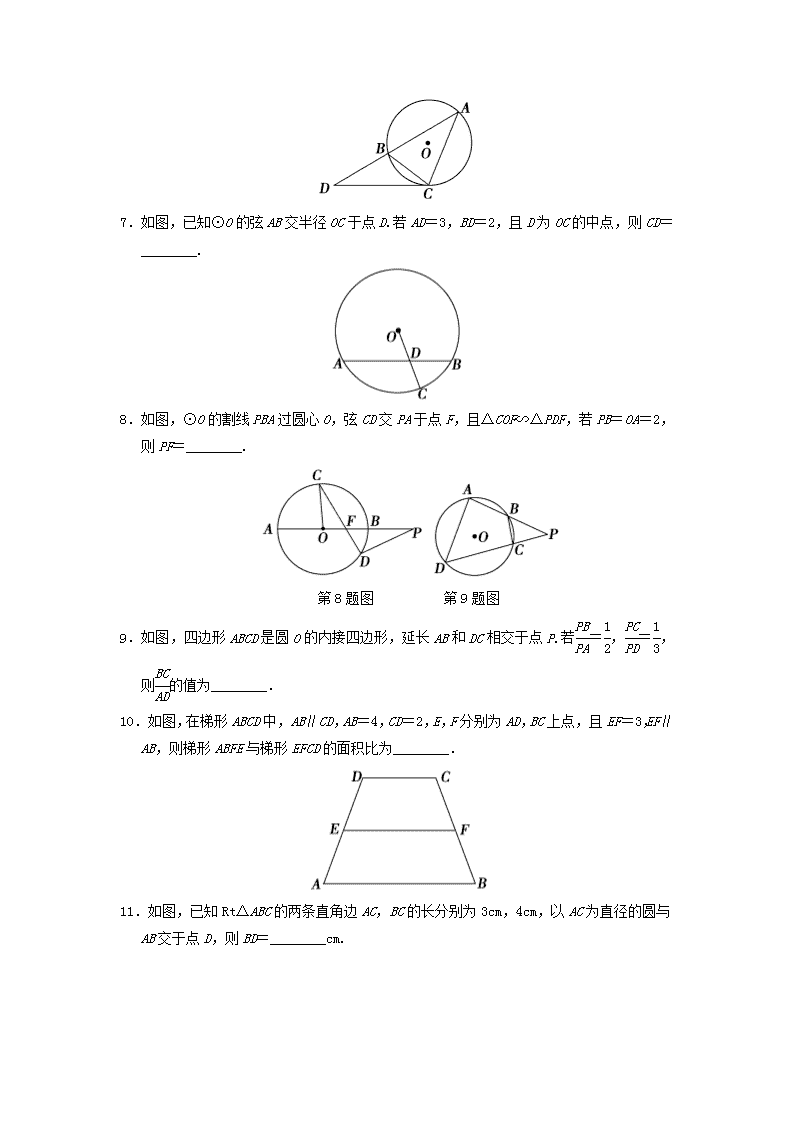7．如图，已知⊙O的弦AB交半径OC于点D.若AD＝3，BD＝2，且D为OC的中点，则CD＝________.‎ ‎8．如图，⊙O的割线PBA过圆心O，弦CD交PA于点F，且△COF∽△PDF，若PB＝OA＝2，则PF＝________.‎ 第8题图　　　　　第9题图　‎ ‎9．如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P.若＝，＝，则的值为________．‎ ‎10．如图，在梯形ABCD中，AB∥CD，AB＝4，CD＝2，E，F分别为AD，BC上点，且EF＝3，EF∥AB，则梯形ABFE与梯形EFCD的面积比为________．‎ ‎11．如图，已知Rt△ABC的两条直角边AC，BC的长分别为‎3 cm，‎4 cm，以AC为直径的圆与AB交于点D，则BD＝________cm.‎ ‎12．如图所示，直线PB与圆O相切于点B，D是弦AC上的点，∠PBA＝∠DBA.若AD＝m，AC＝n，则AB＝________.‎ ‎13．如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF＝3，FB＝1，EF＝，则线段CD的长为________．‎ ‎14．如图所示，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF＝CF＝，AF∶FB∶BE＝4∶2∶1.若CE与圆相切，则线段CE的长为________．‎ ‎　‎ 第14题图　　　 　　第15题图 ‎15．如图，点D在⊙O的弦AB上移动，AB＝4，连接OD，过点D作OD的垂线交⊙O于点C，则CD的最大值为________．‎ B组 ‎1．如图，△ABC的角平分线AD的延长线交它的外接圆于点E.‎ ‎(1)证明：△ABE∽△ADC；‎ ‎(2)若△ABC的面积S＝AD·AE，求∠BAC的大小．‎ ‎2.如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC＝ED.‎ ‎[]‎ ‎(1)证明：CD∥AB；‎ ‎(2)延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G，F四点共圆．‎ ‎3．如图，过圆O外一点M作它的一条切线，切点为A，过A点作直线AP垂直直线OM，垂足为P.‎ ‎(1)证明：OM·OP＝OA2；‎ ‎(2)N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点．过B点的切线交直线ON于K.证明：∠OKM＝90°.‎ ‎4．如图，已知在△ABC中，AB＝AC，D是△ABC外接圆劣弧上的点(不与点A，C重合)，延长BD至E.‎ ‎(1)求证：AD的延长线平分∠CDE；‎ ‎(2)若∠BAC＝30°，△ABC中BC边上的高为2＋，求△ABC外接圆的面积．‎ ‎5．如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E.‎ ‎(1)求证：AB2＝DE·BC；‎ ‎(2)若BD＝9，AB＝6，BC＝9，求切线PC的长．‎ ‎6．如图所示，已知⊙O1和⊙O2相交于A，B两点，过A点作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1，⊙O2于点D，E，DE与AC相交于点P.‎ ‎(1)求证：AD∥EC；‎ ‎(2)若AD是⊙O2的切线，且PA＝6，PC＝2，BD＝9，求AD的长．‎ 参考答案 A组 ‎1．解析　∵AC＝4，AD＝12，∠ACD＝90°，‎ ‎∴CD2＝AD2－AC2＝128，‎ ‎∴CD＝8.‎ 又∵AE⊥BC，∠B＝∠D，‎ ‎∴△ABE∽△ADC，‎ ‎∴＝，‎ ‎∴BE＝＝＝4.‎ 答案　4 ‎2．解析　如图，连接CE，AO，AB.根据A，E是半 ‎ 圆周上的两个三等分点，BC为直径，可得∠CEB ‎ ＝90°，∠CBE＝30°，∠AOB＝60°，故△AOB为 ‎ 等边三角形，AD＝，OD＝BD＝1，∴DF＝，‎ ‎∴AF＝AD－DF＝.‎ 答案　 ‎3．解析　连结DE，由于E是AB的中点，故BE＝.‎ 又CD＝，AB∥DC，CB⊥AB，‎ ‎∴四边形EBCD是矩形．‎ 在Rt△ADE中，AD＝a，F是AD的中点，故EF＝.‎ 答案　 ‎4．解析　如图，连接OA，OB，∠PAO＝∠PBO＝90°，∵∠ACB＝120°，∴∠AOB＝120°.又P，A，O，B四点共圆，故∠APB＝60°.‎ 答案　60°‎ ‎5．解析　由切割线定理知，PC2＝PA·PB，‎ 解得PC＝2.‎ 又OC⊥PC，故CD＝＝＝.‎ 答案　 ‎6．解析　由切割线定理，得CD2＝BD·AD.‎ 因为CD＝6，AB＝5，则36＝BD(BD＋5)，‎ 即BD2＋5BD－36＝0，‎ 即(BD＋9)(BD－4)＝0，所以BD＝4.‎ 因为∠A＝∠BCD，所以△ADC∽△CDB，于是＝.‎ 所以AC＝·BC＝×3＝.‎ 答案　 ‎7．解析　延长CO交圆O于点M，由题意知DC＝，DM＝r.由相交弦定理知AD·DB＝DC·DM，即r2＝6，∴r＝2，∴DC＝.‎ 答案　 ‎8．解析　由相交弦定理可得 BF·AF＝DF·CF，‎ 由△COF∽△PDF可得＝，‎ 即得DF·CF＝PF·OF.∴BF·AF＝PF·OF，‎ 即(PF－2)·(6－PF)＝PF·(4－PF)，解得PF＝3.‎ 答案　3‎ ‎9．解析　∵∠P＝∠P，∠PCB＝∠PAD，∴△PCB∽△PAD.‎ ‎∴＝＝.‎ ‎∵＝，＝，∴＝.‎ 答案　 ‎10．解析　在梯形ABCD中，过C作CG∥AD交AB于G，EF于H.‎ 则HF＝1，GB＝2.又EF∥AB，‎ 即HF∥GB，∴＝＝.‎ ‎∴F应为CB的中点．∴EF为梯形ABCD的中位线．‎ 设梯形EFCD的高为h，则梯形ABCD的高为2h.‎ S梯形ABCD＝＝＝6h，‎ S梯形EFCD＝＝＝.‎ 所以S梯形ABCD∶S梯形EFCD＝12∶5＝，S梯形ABFE∶S梯形EFCD＝7∶5.‎ 答案　7∶5‎ ‎11．解析　如图，连接DC，则CD⊥AB，‎ Rt△ADC∽Rt△ACB.‎ 故＝，即＝，‎ AD＝(cm)，BD＝5－＝(cm)．‎ 答案　 ‎12．解析　∵直线PB与圆相切于点B，且∠PBA＝∠DBA，‎ ‎∴∠ACB＝∠ABP＝∠DBA，由此可得直线AB是△BCD外接圆的切线且B是切点，则由切割线定理得|AB|2＝|AD|·|AC|＝mn，即得|AB|＝.‎ 答案　 ‎13．解析　由相交弦定理得AF·FB＝EF·FC，‎ ‎∴FC＝＝2.‎ 由△AFC∽△ABD，可知＝，‎ ‎∴BD＝＝.‎ 由切割线定理得DB2＝DC·DA，又DA＝4CD，‎ ‎∴4DC2＝DB2＝，∴DC＝.‎ 答案　 ‎14．解析　设AF＝4k，BF＝2k，BE＝k，由DF·FC＝AF·BF，得2＝8k2，即k＝.‎ 所以AF＝2，BF＝1，BE＝，AE＝.‎ 由切割线定理，得CE2＝BE·EA＝×＝，‎ 所以CE＝.‎ 答案　 ‎15．解析　当OD的值最小时，DC最大，易知D为AB的中点时，DB＝DC＝2最大．‎ 答案　2‎ B组 ‎1．(1)证明　由已知条件，可得∠BAE＝∠CAD.‎ 因为∠AEB与∠ACB是同弧上的圆周角，所以∠AEB＝∠ACD.‎ 故△ABE∽△ADC.‎ ‎(2)解　因为△ABE∽△ADC，所以＝，‎ 即AB·AC＝AD·AE.‎ 又S＝AB·ACsin∠BAC，且S＝AD·AE，‎ 故AB·AC·sin∠BAC＝AD·AE.‎ 则sin∠BAC＝1，又∠BAC为三角形内角，所以∠BAC＝90°.‎ ‎2．证明　(1)因为EC＝ED，所以∠EDC＝∠ECD.‎ 因为A，B，C，D四点在同一圆上，所以∠EDC＝∠EBA.‎ 故∠ECD＝∠EBA.所以CD∥AB.‎ ‎ (2)由(1)知AE＝BE.因为EF＝EG，故∠EFD＝∠EGC，从而∠FED＝∠GEC.‎ 连接AF，BG，则△EFA≌△EGB，‎ 故∠FAE＝∠GBE.‎ 又CD∥AB，∠EDC＝∠ECD，‎ 所以∠FAB＝∠GBA.‎ 所以∠AFG＋∠GBA＝180°.‎ 故A，B，G，F四点共圆．‎ ‎3．证明　(1)因为MA是圆O的切线，所以OA⊥AM.又因为AP⊥OM，在Rt△OAM中，由射影定理知，OA2＝OM·OP.‎ ‎(2)因为BK是圆O的切线，BN⊥OK，同(1)，有OB2＝ON·OK，又OB＝OA，所以OP·OM＝ON·OK，‎ 即＝.又∠NOP＝∠MOK，‎ 所以△ONP∽△OMK，‎ 故∠OKM＝∠OPN＝90°.‎ ‎4．(1)证明　如图，设F为AD延长线上一点．‎ ‎∵A、B、C、D四点共圆，‎ ‎∴∠CDF＝∠ABC.‎ 又AB＝AC，∴∠ABC＝∠ACB，‎ 且∠ADB＝∠ACB，‎ ‎∴∠ADB＝∠CDF.‎ 对顶角∠EDF＝∠ADB，‎ 故∠EDF＝∠CDF，‎ 即AD的延长线平分∠CDE.‎ ‎(2)解　设O为外接圆圆心，连结AO交BC于H，‎ 则AH⊥BC.‎ 连结OC，由题意∠OAC＝∠OCA＝15°，∠ACB＝75°，‎ ‎∴∠OCH＝60°.‎ 设圆半径为r，则r＋r＝2＋，得r＝2，外接圆面积为4π.‎ ‎5．(1)证明　∵AD∥BC，∴.‎ ‎∴AB＝CD，∠EDC＝∠BCD.‎ 又PC与⊙O相切，∴∠ECD＝∠DBC.‎ ‎∴△CDE∽△BCD.∴＝.‎ ‎∴CD2＝DE·BC，即AB2＝DE·BC.‎ ‎(2)解　由(1)知，DE＝＝＝4，‎ ‎∵AD∥BC，∴△PDE∽△PBC，‎ ‎∴＝＝.‎ 又∵PB－PD＝9，‎ ‎∴PD＝，PB＝.‎ ‎∴PC2＝PD·PB＝·＝.∴PC＝.‎ ‎6．(1)证明　连接AB，如图所示 ‎∵AC是⊙O1的切线，‎ ‎∴∠BAC＝∠D.‎ 又∵∠BAC＝∠E，∴∠D＝∠E.‎ ‎∴AD∥EC.‎ ‎(2)解　设BP＝x，PE＝y，‎ ‎∵PA＝6，PC＝2，‎ ‎∴xy＝12.①‎ ‎∵根据(1)，可得△ADP∽△CEP，‎ ‎∴＝，即＝，②‎ 由①②，可得 或(负值舍去)，‎ ‎∴DE＝9＋x＋y＝16.‎ ‎∵AD是⊙O2的切线，‎ ‎∴AD2＝DB·DE＝9×16.‎ ‎∴AD＝12.‎