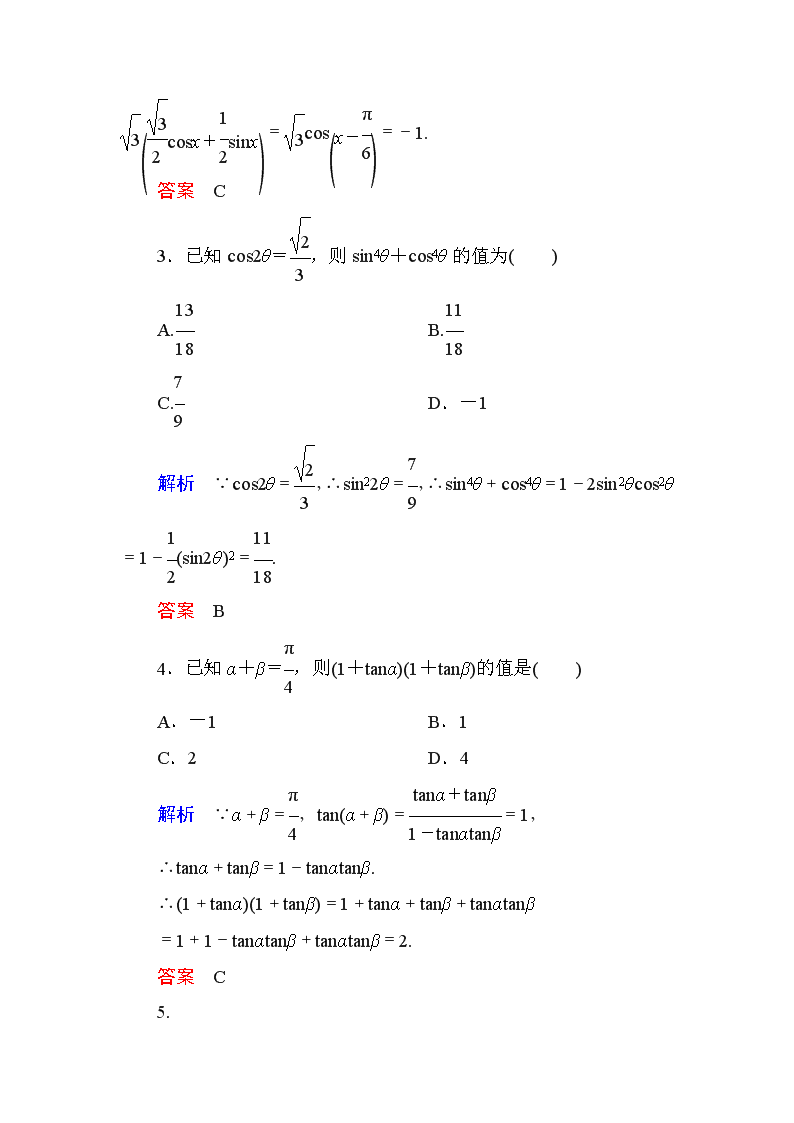35三角恒等变换练习题高考总复习 6页

第五节 三角恒等变换 时间：45 分钟 分值：75 分 一、选择题(本大题共 6 小题，每小题 5 分，共 30 分) 1．已知α为锐角，cosα＝ 5 5 ，则 tan π 4 ＋2α ＝( ) A．－3 B．－1 7 C．－4 3 D．－7 解析 依题意得，sinα＝2 5 5 ，故 tanα＝2，tan2α＝2×2 1－4 ＝－4 3 ， 所以 tan π 4 ＋2α ＝ 1－4 3 1＋4 3 ＝－1 7. 答案 B 2．已知 cos x－π 6 ＝－ 3 3 ，则 cosx＋cos x－π 3 的值是( ) A．－2 3 3 B．±2 3 3 C．－1 D．±1 解析 cosx＋cos x－π 3 ＝cosx＋1 2cosx＋ 3 2 sinx＝3 2cosx＋ 3 2 sinx＝ 3 3 2 cosx＋1 2sinx ＝ 3cos x－π 6 ＝－1. 答案 C 3．已知 cos2θ＝ 2 3 ，则 sin4θ＋cos4θ的值为( ) A.13 18 B.11 18 C.7 9 D．－1 解 析 ∵ cos2θ ＝ 2 3 ， ∴ sin22θ ＝ 7 9 ， ∴ sin4θ ＋ cos4θ ＝ 1 － 2sin2θcos2θ＝1－1 2(sin2θ)2＝11 18. 答案 B 4．已知α＋β＝π 4 ，则(1＋tanα)(1＋tanβ)的值是( ) A．－1 B．1 C．2 D．4 解析 ∵α＋β＝π 4 ，tan(α＋β)＝ tanα＋tanβ 1－tanαtanβ ＝1， ∴tanα＋tanβ＝1－tanαtanβ. ∴(1＋tanα)(1＋tanβ)＝1＋tanα＋tanβ＋tanαtanβ ＝1＋1－tanαtanβ＋tanαtanβ＝2. 答案 C 5. (2014·成都诊断检测)如图，在平面直角坐标系 xOy 中，角α，β 的顶点与坐标原点重合，始边与 x 轴的非负半轴重合，它们的终边分 别与单位圆相交于 A，B 两点，若点 A，B 的坐标为 3 5 ，4 5 和 －4 5 ，3 5 ， 则 cos(α＋β)的值为( ) A．－24 25 B．－ 7 25 C．0 D.24 25 解析 cosα＝3 5 ，sinα＝4 5 ，cosβ＝－4 5 ，sinβ＝3 5 ，cos(α＋β)＝ cosαcosβ－sinαsinβ＝3 5·(－4 5)－4 5·3 5 ＝－24 25.选 A. 答案 A 6．若sin α－π 4 cos2α ＝－ 2，则 sinα＋cosα的值为( ) A．－ 7 2 B．－1 2 C.1 2 D. 7 2 解析 ∵ 2 2 (sinα－cosα)＝－ 2(cos2α－sin2α)， ∴sinα＋cosα＝1 2. 答案 C 二、填空题(本大题共 3 小题，每小题 5 分，共 15 分) 7．若 tan α＋π 4 ＝2 5 ，则 tanα＝________. 解析 ∵tan α＋π 4 ＝tanα＋1 1－tanα ＝2 5 ， ∴5tanα＋5＝2－2tanα. ∴7tanα＝－3，∴tanα＝－3 7. 答案 －3 7 8．(2013·江西卷)函数 y＝sin2x＋2 3sin2x 的最小正周期 T 为 ________． 解析 y＝sin2x＋2 3sin2x＝sin2x－ 3cos2x＋ 3 ＝2sin(2x－π 3)＋ 3，所以 T＝π. 答案 π 9．(2013·新课标全国卷Ⅰ)设当 x＝θ时，函数 f(x)＝sinx－2cosx 取得最大值，则 cosθ＝________. 解析 f(x)＝sinx－2cosx＝ 5( 1 5sinx－ 2 5cosx)＝ 5sin(x－φ)而 sinφ＝ 2 5 ，cosφ＝ 1 5 ，当 x－φ＝π 2 ＋2kπ(k∈Z)时，f(x)取最大值 5， 即θ＝φ＋π 2 ＋2kπ时，f(x)取最大值．cosθ＝cos(φ＋π 2 ＋2kπ)＝－sinφ＝ － 2 5 ＝－2 5 5 . 答案 －2 5 5 三、解答题(本大题共 3 小题，每小题 10 分，共 30 分) 10．已知 tan2θ＝3 4(π 2<θ<π)，求 2cos2θ 2 ＋sinθ－1 2cosθ＋π 4  的值． 解 ∵tan2θ＝ 2tanθ 1－tan2θ ＝3 4 ， ∴tanθ＝－3 或 tanθ＝1 3. 又θ∈(π 2 ，π)，∴tanθ＝－3. ∴ 2cos2θ 2 ＋sinθ－1 2cosθ＋π 4  ＝cosθ＋sinθ cosθ－sinθ ＝1＋tanθ 1－tanθ ＝1－3 1＋3 ＝－1 2. 11．已知函数 f(x)＝2cos ωx＋π 6 (其中ω＞0，x∈R)的最小正周期 为 10π. (1)求ω的值； (2)设α，β∈ 0，π 2 ，f 5α＋5 3π ＝－6 5 ， f 5β－5 6π ＝16 17 ，求 cos(α＋β)的值． 解 (1)∵T＝10π＝2π ω ，∴ω＝1 5. (2)由(1)得 f(x)＝2cos 1 5x＋π 6 ， ∵f 5α＋5π 3 ＝2cos α＋π 2 ＝－2sinα＝－6 5. ∴sinα＝3 5 ，cosα＝4 5. ∵f 5β－5π 6 ＝2cosβ＝16 17 ， ∴cosβ＝ 8 17 ，sinβ＝15 17. ∴cos(α＋β)＝cosαcosβ－sinαsinβ ＝4 5 × 8 17 －3 5 ×15 17 ＝－13 85. 12．(2013·重庆卷)在△ABC 中，内角 A，B，C 的对边分别是 a， b，c，且 a2＋b2＋ 2ab＝c2. (Ⅰ)求 C； (Ⅱ)设 cosAcosB＝3 2 5 ，cosα＋Acosα＋B cos2α ＝ 2 5 ，求 tanα的值． 解 (Ⅰ)因为 a2＋b2＋ 2ab＝c2， 由余弦定理有 cosC＝a2＋b2－c2 2ab ＝－ 2ab 2ab ＝－ 2 2 . 故 C＝3π 4 . (Ⅱ)由题意得 sinαsinA－cosαcosAsinαsinB－cosαcosB cos2α ＝ 2 5 . 因此(tanαsinA－cosA)(tanαsinB－cosB)＝ 2 5 ， tan2αsinAsinB － tanα(sinAcosB ＋ cosAsinB) ＋ cosAcosB ＝ 2 5 ， tan2αsinAsinB－tanαsin(A＋B)＋cosAcosB＝ 2 5 .① 因为 C＝3π 4 ，A＋B＝π 4 ，所以 sin(A＋B)＝ 2 2 ， 因为 cos(A＋B)＝cosAcosB－sinAsinB，即3 2 5 －sinAsinB＝ 2 2 ， 解得 sinAsinB＝3 2 5 － 2 2 ＝ 2 10. 由①得 tan2α－5tanα＋4＝0，解得 tanα＝1 或 tanα＝4.