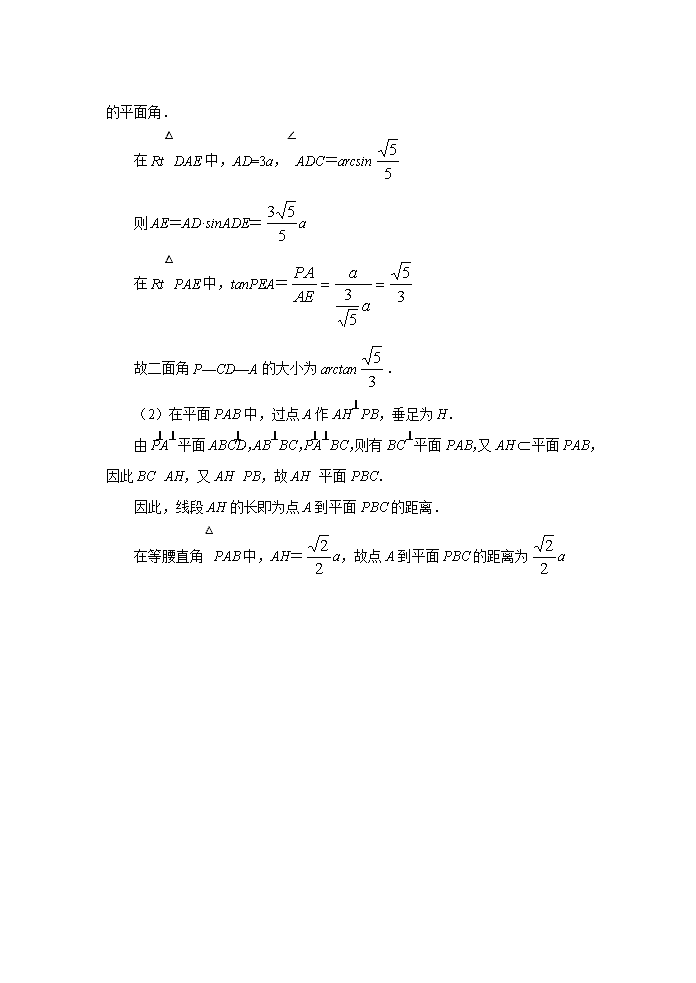高考数学空间距离的计算 3页

第28讲 空间距离的计算 一、 高考要求 空间的距离是从数量角度进一步刻划空间中没有公共点的图形间相对位置的远近程度，是平面几何与立体几何中研究的重要数量．空间距离的求法是教材的重要内容，也是历年高考考查的重点．其中点与点、点到线、点到面的距离为基础．在高考中通常是以一道大题中的某一小题的形式出现，一般是求体积，需算点到面的距离．‎ 二、 两点解读 重点：（1）求距离的一般步骤：①找出或作出有关距离；②证明它符合定义；③归到某三角形中计算．‎ ‎（2）要注意各种距离间的相互转化、等积法及“平行移动”等思想方法．‎ 难点：点到平面的距离的求法．‎ 三、 课前训练 ‎1．若三棱锥的三条侧棱两两垂直，且满足=1，则到平面的距离为 （ D ）‎ ‎（A） （B） （C） （D）‎ ‎2．在棱长为的正方体中，过且平行于平面的平面与平面的距离为 ‎3．已知正方体中，的长为，则与间距离为 一、 典型例题 ‎ 例1已知在中，，它所在平面外一点到三个顶点的距离都是14，那么点到平面的距离是 （ D ）‎ ‎（A）13 （B）11 （C）9 （D）7‎ 例2 在北纬45o 圈上有甲、乙两地，它们的经度分别是东经140°与西经130°，设地球半径为R，则甲乙两地的球面距离是 （ A ）‎ ‎（A） （B） （C） （D）‎ 例3 在正三棱柱中，若，则点到平面的距离为 例4 四边形为正方形，为平面外一点，，二面角为，则到的距离是 例5 如图，在梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝a，AD＝‎3a，且 ‎∠ADC＝arcsin，又PA⊥平面ABCD，PA=a．‎ ‎（I）求二面角P-CD-A的大小（用反三角函数表示）．‎ ‎（II）求点A到平面PBC的距离．‎ 解：（1）如图，在平面ABCD内，过点A作AE⊥CD，垂足为E，连接PE．‎ 由PA⊥平面ABCD，由三垂线定理知PE⊥CD，故∠PEA是二面角P—CD—A 的平面角．‎ 在Rt△DAE中，AD=‎3a，∠ADC＝arcsin 则AE＝AD·sinADE＝a 在Rt△PAE中，tanPEA＝‎ 故二面角P—CD—A的大小为arctan．‎ ‎（2）在平面PAB中，过点A作AH⊥PB，垂足为H．‎ 由PA⊥平面ABCD，AB⊥BC，PA⊥BC，则有BC⊥平面PAB，又AH平面PAB，因此BC⊥AH，又AH⊥PB，故AH⊥平面PBC．‎ 因此，线段AH的长即为点A到平面PBC的距离．‎ 在等腰直角△PAB中，AH＝a，故点A到平面PBC的距离为a