高考文科数学分类汇编专题十四不等式选讲 3页

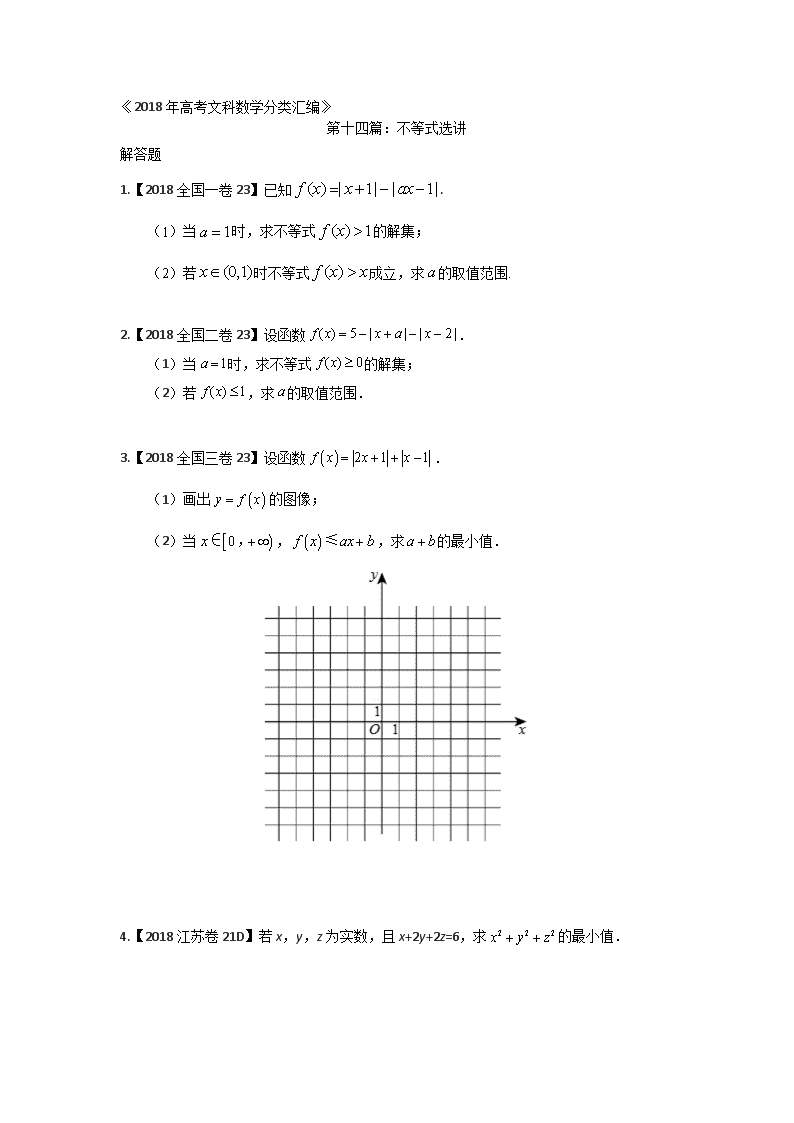
‎《2018年高考文科数学分类汇编》‎ 第十四篇：不等式选讲 解答题 ‎1.【2018全国一卷23】已知.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若时不等式成立，求的取值范围.‎ ‎2.【2018全国二卷23】设函数．‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若，求的取值范围．‎ ‎3.【2018全国三卷23】设函数．‎ ‎（1）画出的图像；‎ ‎（2）当，，求的最小值．‎ ‎4.【2018江苏卷21D】若x，y，z为实数，且x+2y+2z=6，求的最小值．‎ 参考答案 解答题 ‎ 1.解： （1）当时，，即 故不等式的解集为．‎ ‎（2）当时成立等价于当时成立．‎ 若，则当时；‎ 若，的解集为，所以，故．‎ 综上，的取值范围为．‎ ‎2.解：（1）当时，‎ 可得的解集为．‎ ‎（2）等价于．‎ 而，且当时等号成立．故等价于．‎ 由可得或，所以的取值范围是．‎ ‎3.解：（1）的图像如图所示．‎ ‎（2）由（1）知，的图像与轴交点的纵坐标为，且各部分所在直线斜率的最大值为，故当且仅当且时，在成立，因此的最小值为．‎ ‎4.证明：由柯西不等式，得．‎ 因为，所以，‎ 当且仅当时，不等式取等号，此时，‎ 所以的最小值为4．‎