1317全国卷理科高考导数函数题详解版 26页

全国卷13-17高考真题分类汇编：函数、导数及其应用 一.选择题 ‎1.（2015.Ⅱ理5）设函数,( )‎ A．3 B．6 C．9 D．12‎ ‎【解析】选C由已知得，又，所以，故，故选C．‎ ‎2.【2017.Ⅰ理5】函数在单调递减，且为奇函数．若，则满足的的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【考点】函数的奇偶性、单调性 ‎【名师点睛】奇偶性与单调性的综合问题，要重视利用奇、偶函数与单调性解决不等式和比较大小问题，若在R上为单调递增的奇函数，且，则，反之亦成立.‎ ‎3. (2014·Ⅱ理8)设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=　(　　)‎ A.0 B.1 C.2 D.3‎ ‎【解题提示】将函数y=ax-ln（x+1）求导,将x=0代入,利用导数的几何意义求得a.‎ ‎【解析】选D.因为f(x)=ax-ln(x+1),所以f'(x)=a-.所以f(0)=0,且f'(0)=2.联立解得a=3.故选D.‎ ‎4．（2013·Ⅰ文）已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是 (　　)‎ ‎ ‎ A．(－∞，0] B．(－∞，1] C．[－2,1] D．[－2,0]‎ ‎【解析】选D　本题主要考查数形结合思想、函数与方程思想，利用导数研究函数间关系，对分析能力有较高要求．y＝|f(x)|的图像如图所示，y＝ax为过原点的一条直线，当a>0时，与y＝|f(x)|在y 轴右侧总有交点，不合题意．当a＝0时成立．当a<0时，有k≤a<0，其中k是y＝|－x2＋2x|在原点处的切线斜率，显然k＝－2，于是－2≤a<0.综上，a∈[－2,0]．‎ ‎5．（2013·大纲卷理）已知函数f(x)的定义域为(－1,0)，则函数f(2x＋1)的定义域为(　　)‎ A．(－1,1) B. C．(－1,0) D . 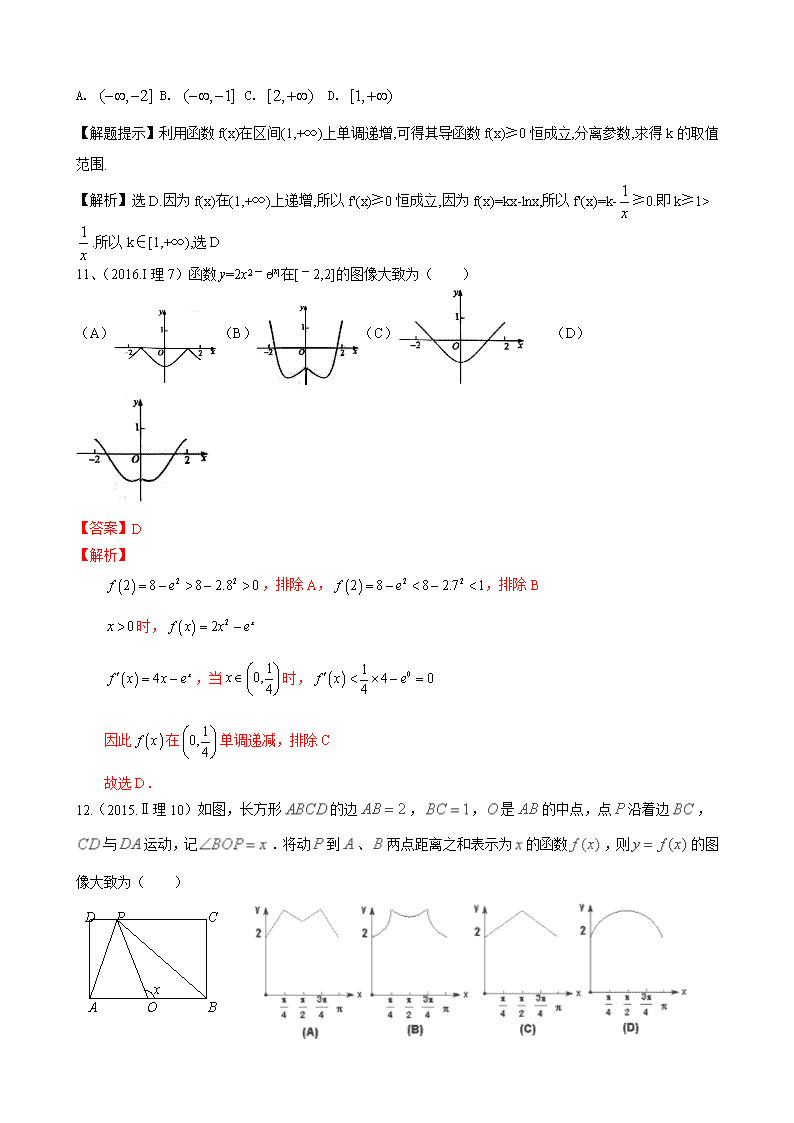‎【解析】选B　本题考查函数定义域问题．由－1<2x＋1<0，解得－1.所以k∈[1,+∞),选D ‎11、（2016.I理7）函数y=2x2–e|x|在[–2,2]的图像大致为（ ）‎ ‎（A）（B）（C） （D）‎ ‎【答案】D ‎【解析】‎ ‎，排除A，，排除B 时，‎ ‎，当时，‎ 因此在单调递减，排除C 故选D．‎ ‎12.（2015.Ⅱ理10）如图，长方形的边，，是的中点，点沿着边，与运动，记．将动到、两点距离之和表示为的函数，则的图像大致为（ ）‎ D P C B ‎ O A x ‎【解析】选B由已知得，当点在边上运动时，即时，；当点在边上运动时，即时，，当时，；当点在边上运动时，即时，，从点的运动过程可以看出，轨迹关于直线对称，且，且轨迹非线型，故选B．‎ ‎13.（2015.Ⅰ文12）设函数的图像与的图像关于直线对称，且，则( )‎ ‎（A） （B） （C） （D）‎ ‎【解析】选C设是函数的图像上任意一点，它关于直线对称为（），由已知知（）在函数的图像上，∴，解得，即，∴，解得，故选C.‎ ‎【解析】由在区间是单调减函数可知，，又，故选.‎ ‎14．（2016.II.理12）已知函数满足，若函数与图像的交点为则（ ）‎ ‎（A）0 （B） （C） （D）‎ ‎【答案】B ‎15.【2017.II理11】若是函数的极值点，则的极小值为（ ）‎ A. B. C. D.1‎ ‎【答案】A ‎【解析】‎ ‎【考点】 函数的极值；函数的单调性 ‎【名师点睛】(1)可导函数y＝f(x)在点x0处取得极值的充要条件是f′(x0)＝0，且在x0左侧与右侧f′(x)的符号不同。‎ ‎(2)若f(x)在(a，b)内有极值，那么f(x)在(a，b)内绝不是单调函数，即在某区间上单调增或减的函数没有极值。‎ ‎16.（2014二理12）设函数函数f(x)=sin.若存在f(x)的极值点x0满足+2.故选C.‎ ‎17.【2017.Ⅲ理11】已知函数有唯一零点，则a=（ ）‎ A． B． C． D．1‎ ‎【答案】C ‎【解析】‎ 试题分析：函数的零点满足，‎ 设，则，‎ 当时，，当时，，函数 单调递减，‎ 当时，，函数 单调递增，‎ 当时，函数取得最小值，‎ 设 ，当时，函数取得最小值 ，‎ ‎【考点】 函数的零点；导函数研究函数的单调性，分类讨论的数学思想 ‎【名师点睛】函数零点的应用主要表现在利用零点求参数范围，若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用. 学科@网 ‎18.（2015.Ⅱ理12）设函数是奇函数的导函数，，当时，，则使得成立的的取值范围是（ ）‎ A． 　　　B．‎ C． 　　　D．‎ ‎【答案】A ‎19.（2015.Ⅰ理12）设函数=,其中a1，若存在唯一的整数，使得0，则的取值范围是（ ）‎ ‎(A)[-，1） (B)[-，） (C)[，） (D)[，1）‎ ‎【解析】设=，，由题知存在唯一的整数，使得在直线的下方.因为，所以当时，＜0，当时，＞0，所以当 时，=，当时，=-1，，直线恒过（1,0）斜率且，故，且，解得≤＜1，故选D.‎ ‎【答案】D 二、 填空题 ‎20.（2015.Ⅰ文14）已知函数的图像在点的处的切线过点，则 .‎ ‎【解析】‎ 试题分析：∵，∴，即切线斜率，‎ 又∵，∴切点为（1，），∵切线过（2,7），∴，解得1.‎ ‎【答案】1‎ ‎21.（2015.Ⅰ理13）若函数f(x)=为偶函数，则a= ‎ ‎【答案】1‎ ‎22．（2013·Ⅰ理）若函数f(x)＝(1－x2)(x2＋ax＋b)的图象关于直线x＝－2对称，则f(x)的最大值为________．‎ ‎【解析】本题考查函数图象的对称性、函数图象的平移、偶函数及函数的极值与最值等知识，意在考查考生综合运用函数知识解答问题的能力、考查考生的运算能力；由函数图象的对称性得相应函数的奇偶性，利用图象平移知识确定函数解析式，再通过求导，研究函数的极值与最值．因为函数f(x)图象关于直线x＝－2对称，所以函数f(x－2)为偶函数，因为f(x)＝(1－x2)(x2＋ax＋b)，所以f(x－2)＝[1－(x－2)2][(x－2)2＋a(x－2)＋b]＝－x4＋(8－a)x3＋(6a－b－23)x2＋(－11a＋4b＋28)x＋(6a－3b－12)为偶函数，所以所以f(x)＝(1－x2)(x2＋8x＋15)，所以f′(x)＝－2x(x2＋8x＋15)＋(1－x2)·(2x＋8)＝－4x3－24x2－28x＋8＝－4(x3＋6x2＋7x－2)＝－4(x＋2)(x2＋4x－1)．令f′(x)＝0，得x＝－2或x＝－2－或x＝－2＋，且当x＜－2－时，f′(x)＞0；当－2－＜x＜－2时，f′(x)＜0；当－2＜x＜－2＋时，f′(x)＞0；当x＞－2＋时，f′(x ‎)＜0，所以当x＝－2－时，f(x)极大值＝16；当x＝－2＋时，f(x)极大值＝16.所以函数f(x)的最大值为16.‎ ‎【答案】16‎ ‎23．（2013·大纲卷文）设f(x)是以2为周期的函数，且当x∈[1,3)时，f(x)＝x－2，则f(－1)＝________.‎ ‎【解析】本题主要考查抽象函数的求值与周期性．因为f(x)是以2为周期的函数，所以f(－1)＝f(－1＋2)＝f(1)＝1－2＝－1.‎ ‎【答案】－1‎ ‎24.【2017.Ⅲ理15】设函数则满足的x的取值范围是_________.‎ ‎【答案】‎ 写成分段函数的形式：，‎ 函数 在区间 三段区间内均单调递增，‎ 且： ，‎ 据此x的取值范围是： .‎ ‎25．（2016.II理16）若直线是曲线的切线，也是曲线的切线，则 ‎ ．‎ ‎【答案】‎ ‎25．（2016.III理15）已知为偶函数，当时，，则曲线在点处的切线方程是_______________。‎ ‎【答案】‎ 二、 解答题 ‎26.（2015.Ⅰ文21）（本小题满分12分）设函数.‎ ‎（I）讨论的导函数的零点的个数；‎ ‎（II）证明：当时.‎ ‎【解析】‎ 试题解析：（I）的定义域为，.‎ 当时,，没有零点；‎ 当时，因为单调递增，单调递增，所以在单调递增.又,当b满足且时，,故当时，存在唯一零点.‎ ‎（II）由（I），可设在的唯一零点为，当时，;‎ 当时，.‎ 故在单调递减，在单调递增，所以当时，取得最小值，最小值为.‎ 由于，所以.‎ 故当时，.‎ ‎27.（2013·Ⅰ文）已知函数f(x)＝ex(ax＋b)－x2－4x，曲线y＝f(x)在点(0，f(0))处的切线方程为y＝4x＋4.‎ ‎(1)求a，b的值；‎ ‎(2)讨论f(x)的单调性，并求f(x)的极大值．‎ 解：本题主要考查导数的基本知识，利用导数判断函数单调性、求极值．‎ ‎(1)f′(x)＝ex(ax＋a＋b)－2x－4.‎ 由已知得f(0)＝4，f′(0)＝4.故b＝4，a＋b＝8.‎ 从而a＝4，b＝4.‎ ‎(2)由(1)知，f(x)＝4ex(x＋1)－x2－4x，‎ f′(x)＝4ex(x＋2)－2x－4＝4(x＋2).‎ 令f′(x)＝0得，x＝－ln 2或x＝－2.‎ 从而当x∈(－∞，－2)∪(－ln 2，＋∞)时，f′(x)>0；当x∈(－2，－ln 2)时，f′(x)<0.‎ 故f(x)在(－∞，－2)，(－ln 2，＋∞)上单调递增，在(－2，－ln 2)上单调递减．‎ 当x＝－2时，函数f(x)取得极大值，极大值为f(－2)＝4(1－e－2)．‎ 由k＜x1＜0知x1＞k显然成立，‎ ‎∴f(－k)＞f(x1)．‎ 再证f(k)＜f(x2)．‎ 同理f(x2)＝，有f(k)－f(x2)＝k－＝(k－x2)＋(k＋x)＜0，‎ ‎∴f(k)＜f(x2)．‎ 综上所述，M＝f(－k)＝－2k3－k，m＝f(k)＝k.‎ ‎28.【2017.Ⅲ理21】已知函数 .‎ ‎（1）若 ，求a的值；‎ ‎（2）设m为整数，且对于任意正整数n ，求m的最小值.‎ ‎【答案】(1) ；‎ ‎(2) ‎ ‎【解析】‎ 试题分析：(1)由原函数与导函数的关系可得x=a是在的唯一最小值点，列方程解得 ；‎ ‎(2)利用题意结合(1)的结论对不等式进行放缩，求得，结合可知实数 的最小值为 ‎ ‎【考点】 导数研究函数的单调性；导数研究函数的最值；利用导数证明不等式 ‎【名师点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出 ，本专题在高考中的命题方向及命题角度 从高考来看，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系． (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用．学科@网 ‎29（2015.Ⅱ理21）设函数.‎ ‎(Ⅰ)证明：f(x)在（-∞，0）单调递减，在（0，+∞）单调递增；‎ ‎(Ⅱ)若对于任意x1,，x2∈[-1,1]，都有｜f(x1)- f(x2)｜≤e-1，求m的取值范围．‎ ‎【答案】(Ⅰ)详见解析；（Ⅱ）．‎ ‎【解析】‎ 试题分析：(Ⅰ)先求导函数，根据的范围讨论导函数在和的符号即可；（Ⅱ）恒成立，等价于．由 是两个独立的变量，故可求研究的值域，由(Ⅰ)可得最小值为，最大值可能是或，故只需，从而得关于的不等式，因不易解出，故利用导数研究其单调性和符号，从而得解．‎ ‎30．（2013·Ⅰ理）设函数f(x)＝x2＋ax＋b，g(x)＝ex(cx＋d)，若曲线y＝f(x)和曲线y＝g(x)都过点P(0,2)，且在点P处有相同的切线y＝4x＋2.‎ ‎(1)求a，b，c，d的值；‎ ‎(2)若x≥－2时，f(x)≤kg(x)，求k的取值范围．‎ 解：本题主要考查利用导数求解曲线的切线，利用函数的导数研究函数的最值，进而解答不等式恒成立问题，意在考查考生综合运用导数这一重要工具解答函数与不等式问题的综合能力．‎ ‎(1)由已知得f(0)＝2，g(0)＝2，f′(0)＝4，g′(0)＝4.‎ 而f′(x)＝2x＋a，g′(x)＝ex(cx＋d＋c)，故b＝2，d＝2，a＝4，d＋c＝4.‎ 从而a＝4，b＝2，c＝2，d＝2.‎ ‎(2)由(1)知，f(x)＝x2＋4x＋2，g(x)＝2ex(x＋1)．‎ 设函数F(x)＝kg(x)－f(x)＝2kex(x＋1)－x2－4x－2，‎ 则F′(x)＝2kex(x＋2)－2x－4＝2(x＋2)(kex－1)．‎ 由题设可得F(0)≥0，即k≥1.‎ 令F′(x)＝0得x1＝－lnk，x2＝－2.‎ ‎(ⅰ)若1≤k＜e2，则－2＜x1≤0，从而当x∈(－2，x1)时，F′(x)＜0；当x∈(x1，＋∞)时，F′(x)＞0，即F(x)在(－2，x1)上单调递减，在(x1，＋∞)上单调递增，故F(x)在[－2，＋∞)的最小值为F(x1)．而F(x1)＝2x1＋2－x－4x1－2＝－x1(x1＋2)≥0.‎ 故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎(ⅱ)若k＝e2，则F′(x)＝2e2(x＋2)(ex－e－2)．从而当x＞－2时，F′(x)＞0，即F(x)在(－2，＋∞)上单调递增．而F(－2)＝0，故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎(ⅲ)若k＞e2，则F(－2)＝－2ke－2＋2＝－2e－2(k－e2)＜0.从而当x≥－2时，f(x)≤kg(x)不可能恒成立．‎ 综上，k的取值范围是[1，e2]．‎ ‎31、（2016.III.）设函数，其中，记的最大值为．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）求；‎ ‎（Ⅲ）证明．‎ 解析：（Ⅰ）．‎ ‎（Ⅱ）当时，‎ 因此，． ………4分 当时，将变形为．‎ 令，则是在上的最大值，，，且当时，取得极小值，极小值为．‎ 令，解得（舍去），．‎ ‎32、（2016.II.理21）(Ⅰ)讨论函数的单调性，并证明当时，； ‎ ‎(Ⅱ)证明：当时，函数有最小值.设的最小值为，求函数的值域．‎ ‎【解析】⑴证明：‎ ‎ ‎ ‎ ∵当时，‎ ‎ ∴在上单调递增 ‎ ∴时，‎ ‎ ∴‎ ‎⑵ ‎ ‎ ‎ ‎ 由(1)知，当时，的值域为，只有一解．‎ ‎ 使得，‎ 当时，单调减；当时，单调增 记，在时，，∴单调递增 ‎∴．‎ ‎33.【2017.Ⅰ理21】已知函数.‎ ‎（1）讨论的单调性；‎ ‎（2）若有两个零点，求a的取值范围.‎ ‎【解析】‎ 试题分析：（1）讨论单调性，首先进行求导，发现式子特点后要及时进行因式分解，在对按，进行讨论，写出单调区间；（2）根据第（1）题，若，至多有一个零点.若，当时，取得最小值，求出最小值，根据，，进行讨论，可知当有2个零点，设正整数满足，则 ‎.由于，因此在有一个零点.所以的取值范围为.‎ ‎【考点】含参函数的单调性，利用函数零点求参数取值范围.‎ ‎【名师点睛】研究函数零点问题常常与研究对应方程的实根问题相互转化.已知函数有2个零点求参数取值范围，第一种方法是分离参数，构造不含参数的函数，研究其单调性、极值、最值，判断与其交点的个数，从而求出a的范围；第二种方法是直接对含参函数进行研究，研究其单调性、极值、最值，注意点是若有2个零点，且函数先减后增，则只需其最小值小于0，且后面还需验证有最小值两边存在大于0的点. 学科@网 ‎34．（2013·II理）已知函数f(x)＝ex－ln(x＋m)．‎ ‎(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；‎ ‎(2)当m≤2时，证明f(x)>0.‎ 解：考查利用导数研究函数的单调性以及运用导数方法证明不等式等知识．意在考查考生综合运用知识的能力以及化归与转化的思想．‎ ‎(1)f′(x)＝ex－.‎ 由x＝0是f(x)的极值点得f′(0)＝0，所以m＝1.‎ 于是f(x)＝ex－ln(x＋1)，定义域为(－1，＋∞)，‎ f′(x)＝ex－.‎ 函数f′(x)＝ex－在(－1，＋∞)，上单调递增且f′(0)＝0，因此当x∈(－1,0)时，f′(x)<0；当x∈(0，＋∞)时，f′(x)>0.‎ 所以f(x)在(－1,0)上单调递减，在(0，＋∞)上单调递增．‎ ‎(2) 证明：当m≤2，x∈(－m，＋∞)时，ln(x＋m)≤ln(x＋2)，‎ 故只需证明当m＝2时，f(x)>0.‎ 当m＝2时，函数f′(x)＝ex－在(－2，＋∞)上单调递增，又f′(－1)<0，f′(0)>0，故f′(x)＝0在(－2，＋∞)上有唯一实根x0，且x0∈(－1,0)．‎ 当x∈(－2，x0)时，f′(x)<0；当x∈(x0，＋∞)时，f′(x)>0，从而当x＝x0时，f(x)取得最小值．‎ 由f′(x0)＝0得ex0＝，ln(x0＋2)＝－x0，‎ 故f(x)≥f(x0)＝＋x0＝>0.‎ 综上，当m≤2时，f(x)>0.‎ ‎35.【2017.II理】已知函数，且。‎ ‎(1)求；‎ ‎(2)证明：存在唯一的极大值点，且。‎ ‎【答案】(1)；‎ ‎(2)证明略。‎ ‎【解析】‎ ‎（2）由（1）知 ，。‎ 设，则。‎ 当 时， ；当 时， ，‎ 所以 在 单调递减，在 单调递增。‎ ‎【考点】 利用导数研究函数的单调性；利用导数研究函数的极值 ‎【名师点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出 ，本专题在高考中的命题方向及命题角度 从高考来看，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系。 (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数。 (3)利用导数求函数的最值(极值)，解决生活中的优化问题。 (4)考查数形结合思想的应用。学科@网 ‎36.（2016.I理21）已知函数有两个零点.‎ ‎（I）求a的取值范围；‎ ‎（II）设x1，x2是的两个零点，证明：+x2<2.‎ 解：⑴ 由已知得：‎ ‎① 若，那么，只有唯一的零点，不合题意；‎ ‎② 若，那么，‎ 所以当时，，单调递增 当时，，单调递减 即：‎ ‎↓‎ 极小值 ‎↑‎ 故在上至多一个零点，在上至多一个零点 由于，，则，‎ 根据零点存在性定理，在上有且仅有一个零点．‎ 而当时，，，‎ 故 则的两根，， ，因为，故当或时，‎ 因此，当且时，‎ 又，根据零点存在性定理，在有且只有一个零点．‎ 此时，在上有且只有两个零点，满足题意．‎ ‎③ 若，则，‎ 当时，，，‎ 即，单调递增；‎ 当时，，，即，单调递减；‎ 当时，，，即，单调递增．‎ 即：‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ ‎↑‎ 极大值 ‎↓‎ 极小值 ‎↑‎ 而极大值 故当时，在处取到最大值，那么恒成立，即无解 而当时，单调递增，至多一个零点 此时在上至多一个零点，不合题意．‎ ‎④ 若，那么 当时，，，即，‎ 单调递增 当时，，，即，‎ 单调递增 又在处有意义，故在上单调递增，此时至多一个零点，不合题意．‎ ‎⑤ 若，则 当时，，，即，‎ 单调递增 当时，，，即，‎ 单调递减 当时，，，即，‎ 单调递增 即：‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ ‎↑‎ 极大值 ‎↓‎ 极小值 ‎↑‎ 故当时，在处取到最大值，那么恒成立，即 无解 当时，单调递增，至多一个零点 此时在上至多一个零点，不合题意．‎ 综上所述，当且仅当时符合题意，即的取值范围为．‎ ⑵ 由已知得：，不难发现，，‎ 故可整理得：‎ 设，则 那么，当时，，单调递减；当时，，单调递增．‎ 设，构造代数式：‎ 设，‎ 则，故单调递增，有．‎ 因此，对于任意的，．‎ 由可知、不可能在的同一个单调区间上，不妨设，则必有 令，则有 而，，在上单调递增，因此：‎ 整理得：．‎ ‎37(2015.Ⅰ理21)(本小题满分12分)‎ 已知函数f(x)＝ ‎ ‎(Ⅰ)当a为何值时，x轴为曲线 的切线；‎ ‎(Ⅱ)用 表示m，n中的最小值，设函数 ，讨论h(x)零点的个数 ‎（I）设曲线y=f(x)与x轴相切于点，则 解得.因此，当 ‎（II）当 是的零点 综上，当 ‎38. (2014·Ⅱ理21)(本小题满分12分)已知函数f(x)=ex-e-x-2x.‎ ‎(1)讨论f(x)的单调性.‎ ‎(2)设g (x)= f(2x)-4b f(x),当x>0时,g(x)>0,求b的最大值.‎ ‎(3)已知1.4142<<1.4143,估计ln2的近似值(精确到0.001).‎ ‎【解题提示】(1)求f'(x),结合f(x)的符号判断单调性.‎ ‎(2)构造函数,分离出b,求得b的最大值.‎ ‎(3)利用第(2)问的结论,估计ln2的近似值.‎ ‎【解析】 -2≥0，等号仅当x=0时成立.‎ 所以f(x)在（-∞,+∞）单调递增.‎ ‎(2) ‎ +（8b-4）x,g′(x)=2［+(4b-2)］‎ ‎= ‎ ①当b≤2时，g′(x)≥0，等号仅当x=0时成立，所以g(x)在(-∞,+∞)单调递增.而g(0)=0，所以对任意x＞0，g(x)＞0.‎ ‎②当b＞2时，若x满足2＜＜2b-2,即0＜x＜ln(b-1+)时，g′(x)＜0.而g(0)=0，因此当0＜x＜ln(b-1+ )时，g(x)＜0.综上，b的最大值为2.‎ ‎（3）由（2）知，g(ln )＝-2b+2(2b-1)ln 2，‎ 当b=2时，g(ln )= -4 +6ln 2＞0，ln 2＞＞0.692 8；‎ 当b= +1时，ln(b-1+ )=ln ,‎ g(ln )=--2+(3+2)ln 2＜0，‎ ln 2＜＜0.693 4.所以ln 2的近似值为0.693.‎ ‎39. (2014·Ⅱ文21)(本小题满分12分)已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2.‎ ‎(1)求a.‎ ‎(2)证明:当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点.‎ ‎【解题提示】(1)利用切线的性质结合已知条件求得a.‎ ‎(2)由f(x)=kx-2,化为“k= g(x)”型,通过研究函数g(x)的性质,画出g(x)的草图,完成证明.‎ ‎【解析】(1)因为f(x)=x3-3x2+ax+2,所以f'(x)=3x2-6x+a,f'(0)=a,‎ 设切点A(0,2),切线与x轴交点为B(-2,0),则kAB=f'(0),即=a,‎ 所以,a=1.‎ ‎(2)当k<1时,令f(x)-kx+2=x3-3x2+x-kx+4=0.则x2-3x+1+=k,x≠0,‎ 令g(x)=x2-3x+1+.则g'(x)=2x-3-=.‎ 令h(x)=2x3-3x2-4,则h'(x)=6x2-6x=6x(x-1),‎ 所以当x∈(0,1)时,h'(x)<0,h(x)递减.‎ 当x∈(-∞,0)或(1,+∞)时,h'(x)>0,h(x)递增;且h(0)<0,h(2)=0.‎ 所以当x<2时,h(x)<0,g'(x)<0,g(x)在(-∞,0),(0,2)上递减;‎ 当x>2时,h(x)>0,g'(x)>0,g(x)在(0,+∞)上递增;‎ 所以当x∈(0,2)∪(0,+∞)时,g(x)≥g(2)=1,‎ 当x∈(-∞,0)时,单调递减,且g(x)∈(-∞,+∞).‎ 所以当k<1时,g(x)=k仅有一个根,图像如图所示,‎ 所以,当k<1时,y=f(x)与y=kx-2仅有一个交点.‎ ‎360．（2013·大纲卷文）已知函数f(x)＝x3＋3ax2＋3x＋1.‎ ‎(1)当a＝－时，讨论f(x)的单调性；‎ ‎(2)若x∈[2，＋∞)时，f(x)≥0，求a的取值范围．‎ 解：本题主要考查导数与单调性的关系、不等式的性质与解法；考查逻辑推理能力、分析问题和解决问题的能力、运算能力；考查转化的思想、分类讨论的思想、函数与方程的思想．‎ ‎(1)当a＝－时，f(x)＝x3－3x2＋3x＋1，‎ f′(x)＝3x2－6x＋3.‎ 令f′(x)＝0，得x1＝－1，x2＝＋1.‎ 当x∈(－∞，－1)时，f′(x)>0，f(x)在(－∞，－1)是增函数；‎ 当x∈(－1，＋1)时，f′(x)<0，f(x)在(－1，＋1)是减函数；‎ 当x∈(＋1，＋∞)时，f′(x)>0，f(x)在(＋1，＋∞)是增函数．‎ ‎(2)由f(2)≥0得a≥－.‎ 当a≥－，x∈(2，＋∞)时，‎ f′(x)＝3(x2＋2ax＋1)≥3＝3·(x－2)>0，‎ 所以f(x)在(2，＋∞)是增函数，于是当x∈[2，＋∞)时，f(x)≥f(2)≥0.‎ 综上，a的取值范围是－，＋∞.‎