高考数学高考必备知识点总结精华版 18页

高考前重点知识回顾 第一章-集合 ‎（一）、集合：集合元素的特征：确定性、互异性、无序性. ‎ ‎1、集合的性质：①任何一个集合是它本身的子集，记为；‎ ‎ ②空集是任何集合的子集，记为；‎ ‎ ③空集是任何非空集合的真子集；‎ ‎①n个元素的子集有2n个. n个元素的真子集有2n －1个. n个元素的非空真子集有2n－2个.‎ ‎[注]①一个命题的否命题为真，它的逆命题一定为真.否命题逆命题.‎ ‎ ②一个命题为真，则它的逆否命题一定为真. 原命题逆否命题.‎ ‎2、集合运算：交、并、补.‎ ‎（三）简易逻辑 构成复合命题的形式：p或q(记作“p∨q” )；p且q(记作“p∧q” )；非p(记作“┑q” ) 。‎ ‎1、“或”、 “且”、 “非”的真假判断 ‎4、四种命题的形式及相互关系：‎ 原命题：若P则q； 逆命题：若q则p；‎ 否命题：若┑P则┑q；逆否命题：若┑q则┑p。‎ ‎①、原命题为真，它的逆命题不一定为真。‎ ‎②、原命题为真，它的否命题不一定为真。‎ ‎③、原命题为真，它的逆否命题一定为真。‎ ‎6、如果已知pq那么我们说，p是q的充分条件，q是p的必要条件。‎ 若pq且qp,则称p是q的充要条件，记为p⇔q.‎ 第二章-函数 一、函数的性质 ‎（1）定义域： （2）值域：‎ ‎（3）奇偶性：（在整个定义域内考虑）‎ ‎ ①定义：偶函数：，‚奇函数：‎ ‎ ②判断方法步骤：a.求出定义域；b.判断定义域是否关于原点对称；c.求；d.比较或的关系。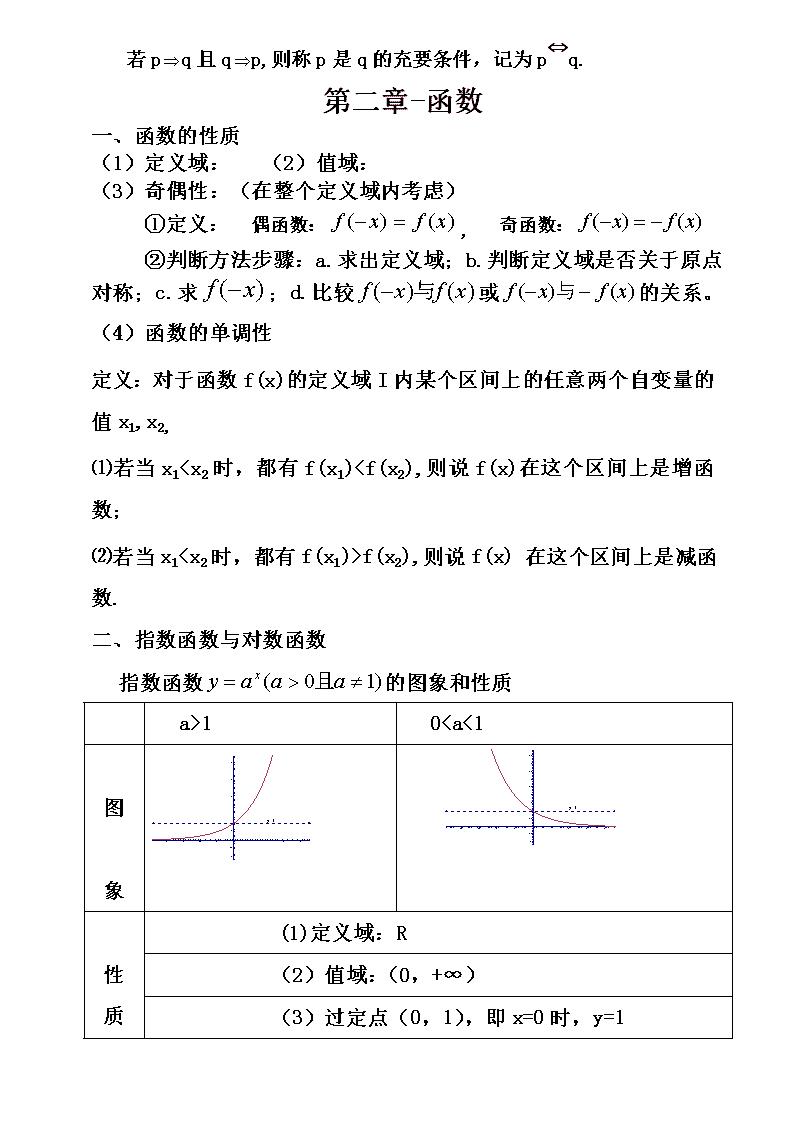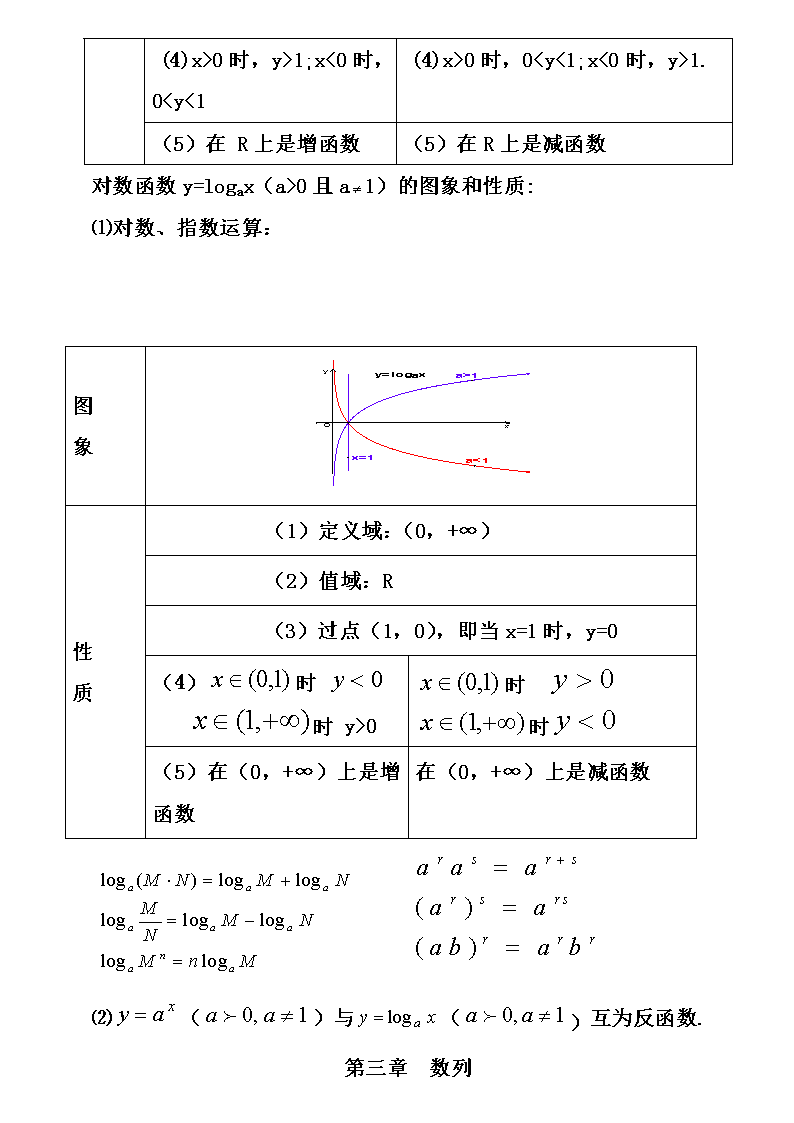 ‎ ‎（4）函数的单调性 定义：对于函数f(x)的定义域I内某个区间上的任意两个自变量的值x1,x2,‎ ‎⑴若当x1f(x2),则说f(x) 在这个区间上是减函数.‎ 二、指数函数与对数函数 指数函数的图象和性质 a>1‎ ‎00时，y>1;x<0时，00时，01.‎ ‎（5）在 R上是增函数 ‎（5）在R上是减函数 对数函数y=logax（a>0且a1）的图象和性质:‎ 图 象 性 质 ‎（1）定义域：（0，+∞）‎ ‎（2）值域：R ‎（3）过点（1，0），即当x=1时，y=0‎ ‎（4）时 ‎ 时 y>0‎ 时 ‎ 时 ‎（5）在（0，+∞）上是增函数 在（0，+∞）上是减函数 ‎⑴对数、指数运算：‎ ‎ ‎ ‎⑵（）与（）互为反函数.‎ ‎ 第三章 数列 ‎1. ⑴等差、等比数列：‎ 等差数列 等比数列 定义 递推公式 ‎；‎ ‎；‎ 通项公式 ‎（）‎ 中项公式 前项和 重要性质 则 ‎（2）数列{}的前项和与通项的关系：‎ 第四章-三角函数 一.三角函数 ‎1、角度与弧度的互换关系：360°=2 ；180°= ； ‎ ‎1rad＝°≈57.30°=57°18ˊ；1°＝≈0.01745（rad）‎ 注意：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.‎ ‎2、弧长公式：. 扇形面积公式：‎ ‎3、三角函数： ； ； ； ‎ ‎4、三角函数在各象限的符号：（一全二正弦，三切四余弦）‎ ‎5、同角三角函数的基本关系式： ‎ ‎6、诱导公式：‎ ‎ ‎ ‎ ‎ ‎7、两角和与差公式 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 8、 二倍角公式是：‎ ‎ sin2=‎ ‎ cos2===‎ ‎ 2=。‎ 辅助角公式asinθ+bcosθ=sin(θ+)，这里辅助角 所在象限由a、b的符号确定，角的值由tan=确定。‎ ‎9、特殊角的三角函数值：‎ ‎0‎ sin ‎0‎ ‎1‎ ‎0‎ cos ‎1‎ ‎0‎ ‎0‎ tan ‎0‎ ‎1‎ 不存在 ‎0‎ 不存在 cot 不存在 ‎1‎ ‎0‎ 不存在 ‎0‎ ‎10、正弦定理 （R为外接圆半径）．‎ ‎ 余弦定理 c2 = a2+b2－2bccosC，‎ ‎ b2 = a2+c2－2accosB，‎ ‎ a2 = b2+c2－2bccosA．‎ 面积公式：‎ ‎11.或（）的周期.‎ ‎12.的对称轴方程是（），对称中心（）；的对称轴方程是（），对称中心（）；的对称中心（）.‎ 第五章-平面向量 ‎(1)向量的基本要素：大小和方向. ‎(2)向量的长度：即向量的大小，记作｜｜.‎  ‎(3)特殊的向量：零向量＝O｜｜＝O. 单位向量为单位向量｜｜＝1. ‎(4)相等的向量：大小相等，方向相同(ｘ1，ｙ1)＝（ｘ2，ｙ2）‎ ‎(5) 相反向量：=-=-+=‎ ‎(6)平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作∥.平行向量也称为共线向量.‎ ‎（7）.向量的运算 运算类型 几何方法 坐标方法 运算性质 向量的 加法 1. 平行四边 形法则 ‎2.三角形法则 向量的 减法 三角形法则 ‎,‎ 数 乘 向 量 ‎1.是一个向量,满足:‎ ‎2.>0时, 同向;<0时, 异向;‎ ‎=0时, .‎ 向 量 的 数 量 积 是一个数 ‎1.时，‎ ‎ ‎ ‎(8)两个向量平行的充要条件 ‎∥ (¹)‎ ‎(9)两个向量垂直的充要条件 ‎ ⊥·=0 x1·x2+y1·y2=0‎ ‎(10)两向量的夹角公式：cosθ==‎ ‎0≤θ≤180°,‎ 附：三角形的四个“心”；‎ ‎1、内心：内切圆的圆心，角平分线的交点 ‎2、外心：外接圆的圆心，垂直平分线的交点 ‎ 3、重心：中线的交点 ‎ 4、垂心：高的交点 ‎(11)△ABC的判定：‎ ‎△ABC为直角△∠A + ∠B =‎ ‎＜△ABC为钝角△∠A + ∠B＜‎ ‎＞△ABC为锐角△∠A + ∠B＞‎ ‎(11)平行四边形对角线定理：对角线的平方和等于四边的平方和.‎ 第六章-不等式 ‎1.几个重要不等式 ‎（1） 当且仅当，(a－b)2≥0(a、b∈R)‎ ‎（2）‎ ‎（3），则；‎ ‎（4）；‎ ‎⑸若a、b∈R+，，则 ‎；‎ ‎2、解不等式 ‎（1）一元一次不等式 ‎ ‎① ②‎ ‎（2）一元二次不等式 ‎ 第七章-直线和圆的方程 一、解析几何中的基本公式 ‎1.两点间距离：若，则 ‎2.平行线间距离：若 ‎ 则： ‎ 注意：x，y对应项系数应相等。‎ ‎3.点到直线的距离：‎ 则P到l的距离为：‎ ‎4.直线与圆锥曲线相交的弦长公式： 消y：，务必注意若l与曲线交于A则：‎ ‎5.若A，P（x，y）,P为AB中点，则 ‎6.直线的倾斜角（0°≤＜180°）、斜率:‎ ‎7.过两点. ‎ ‎8.直线l1与直线l2的的平行与垂直 ‎（1）若l1，l2均存在斜率且不重合：①l1//l2 k1=k2 ②l1l2 k1k2=－1‎ ‎ （2）若 ‎ 若A1、A2、B1、B2都不为零 ‎ ‎ l1//l2； ‚l1l2 A1A2+B1B2=0；‎ ‎9.直线方程的五种形式 名称 方程 ‎ 斜截式： y=kx+b ‎ 点斜式： ‎ 两点式： （x1≠x2 ）‎ 截距式： ‎ 一般式： （其中A、B不同时为零）‎ 10. 圆的方程 ‎ ‎（1）标准方程： ， ‎ ‎。‎ ‎（2）一般方程：，（‎ ‎ 半径 特例：圆心在坐标原点，半径为的圆的方程是：.‎ 注：圆的参数方程：（为参数）.‎ 特别地，以(0，0)为圆心，以r为半径的圆的参数方程为 ‎（3）点和圆的位置关系：给定点及圆.‎ ‎①在圆内 ‎②在圆上 ‎③在圆外 ‎（4）直线和圆的位置关系：‎ ‎ 设圆圆：； ‎ ‎ 直线：；‎ ‎ 圆心到直线的距离.‎ ‎ ①时，与相切；‎ ‎ ②时，与相交；‎ ‎ ③时，与相离. ‎ ‎ ‎ 第八章-圆锥曲线方程 一、椭圆 ‎1.定义Ⅰ：若F1，F2是两定点，P为动点，且 （为常数）则P点的轨迹是椭圆。‎ ‎2.标准方程： ‎ 长轴长=，短轴长=2b 焦距：2c 准线方程：，‎ 离心率： 焦点：或.‎ 二、双曲线 ‎1、定义：若F1，F2是两定点，（为常数），则动点P的轨迹是双曲线。‎ ‎2.性质 ‎（1）方程： ‎ 实轴长=，虚轴长=2b焦距：2c 准线方程： ‎ ‎ 离心率. 准线距（两准线的距离）；通径. ‎ 参数关系.‎ （2） 若双曲线方程为渐近线方程：‎ ‎ ⑶等轴双曲线：双曲线称为等轴双曲线，其渐近线方程为，离心率. ‎ 三、抛物线 ‎ 1.定义：到定点F与定直线l的距离相等的点的轨迹是抛物线。‎ 即：到定点F的距离与到定直线l的距离之比是常数e（e=1）。‎ ‎ 2.图形：‎ ‎ ‎ ‎3.性质：方程：（焦点到准线的距离）；‎ ‎ 焦点： ，通径；‎ ‎ 准线： ；离心率 ‎ ‎ 第九章-立体几何 一、判定两线平行的方法 1、 平行于同一直线的两条直线互相平行 2、 垂直于同一平面的两条直线互相平行 3、 如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行 4、 如果两个平行平面同时和第三个平面相交，那么它们的交线平行 二． 判定线面平行的方法 a) 据定义：如果一条直线和一个平面没有公共点 b) 如果平面外的一条直线和这个平面内的一条直线平行，则这条直线和这个平面平行 c) 两面平行，则其中一个平面内的直线必平行于另一个平面 d) 平面外的两条平行直线中的一条平行于平面，则另一条也平行于该平面 e) 平面外的一条直线和两个平行平面中的一个平面平行，则也平行于另一个平面 三、判定面面平行的方法 ‎⑴由定义知：“两平行平面没有公共点”。‎ ‎ ⑵由定义推得：“两个平面平行，其中一个平面内的直线必平行于另一个平面。‎ ‎ ⑶两个平面平行的性质定理：“如果两个平行平面同时和第三个平面相交，那么它们的交线平行”。‎ ‎ ⑷一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。‎ ‎ ⑸夹在两个平行平面间的平行线段相等。‎ ‎ ⑹经过平面外一点只有一个平面和已知平面平行。‎ 四、面面平行的性质 ‎1、两平行平面没有公共点 ‎2、两平面平行，则一个平面上的任一直线平行于另一平面 ‎3、两平行平面被第三个平面所截，则两交线平行 4、 垂直于两平行平面中一个平面的直线，必垂直于另一个平面 五、判定线面垂直的方法 ‎1、定义：如果一条直线和平面内的任何一条直线都垂直，则线面垂直 ‎2、如果一条直线和一个平面内的两条相交线垂直，则线面垂直 ‎3、如果两条平行直线中的一条垂直于一个平面，则另一条也垂直于该平面 ‎4、一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面 ‎5、如果两个平面垂直，那么在一个平面内垂直它们交线的直线垂直于另一个平面 六、判定两线垂直的方法 1、 定义：成角 2、 直线和平面垂直，则该线与平面内任一直线垂直 3、 一条直线如果和两条平行直线中的一条垂直，它也和另一条垂直 七、判定面面垂直的方法 1、 定义：两面成直二面角,则两面垂直 2、 一个平面经过另一个平面的一条垂线，则这个平面垂直于另一平面 八、面面垂直的性质 1、 二面角的平面角为 2、 在一个平面内垂直于交线的直线必垂直于另一个平面 3、 相交平面同垂直于第三个平面，则交线垂直于第三个平面 九、各种角的范围 ‎ ‎ 1、异面直线所成的角的取值范围是： ‎ ‎2、直线与平面所成的角的取值范围是： ‎ ‎3、斜线与平面所成的角的取值范围是： ‎ ‎4、二面角的大小用它的平面角来度量；取值范围是： ‎ 十、面积和体积 ‎ ‎ 1.‎ ‎ ‎ ‎ ‎ ‎ 2、 ‎ ‎ 3、球的表面积公式：.球的体积公式：.‎ ‎ 4、圆柱体积：（为半径，为高）‎ ‎ 圆锥体积：（为半径，为高）‎ ‎ 锥体体积：（为底面积，为高） ‎ ‎5、面积比是相似比的平方，体积比是相似比的立方 第十章-概率与统计 ‎1.必然事件P(A)=1，不可能事件P(A)=0，随机事件的定义 0