高考数学数列求通项公式和及求和 6页

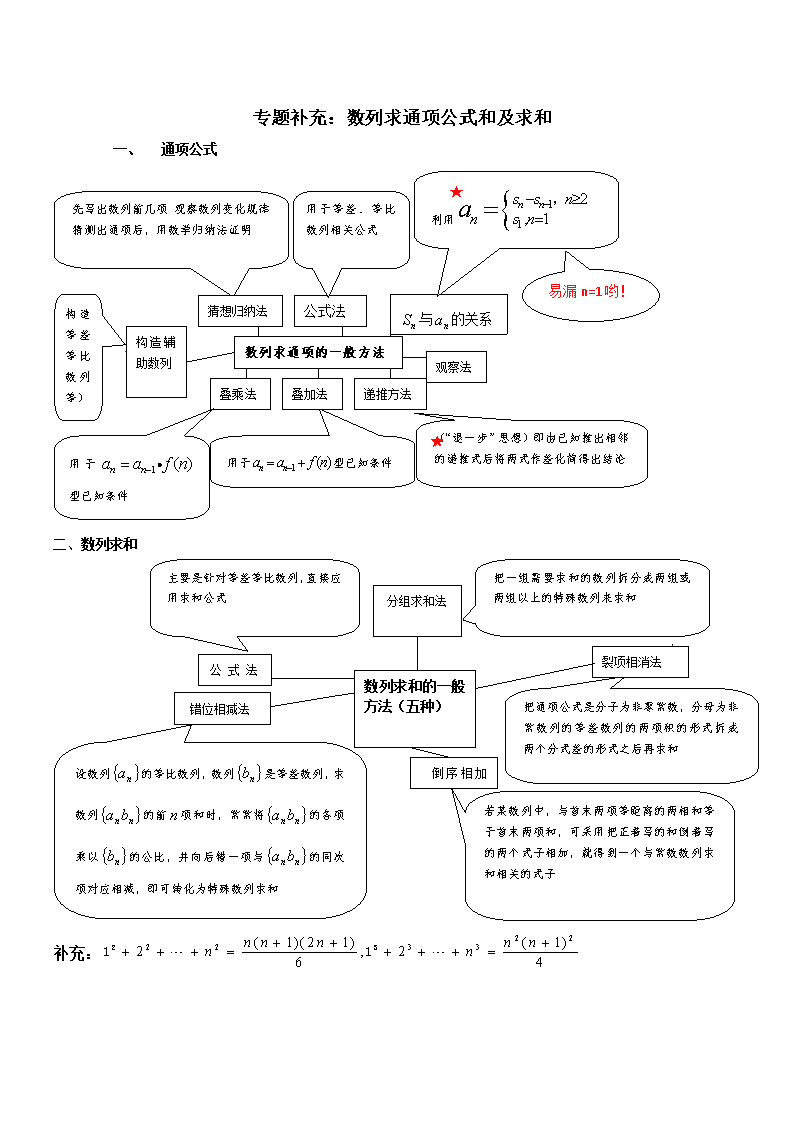
专题补充：数列求通项公式和及求和 一、 通项公式 用于型已知条件 ‎ 先写出数列前几项 观察数列变化规律猜测出通项后，用数学归纳法证明 ‎（“退一步”思想）即由已知推出相邻的递推式后将两式作差化简得出结论 ‎ 构造等差等比数列等）‎ 公式法 叠加法 用于等差、等比数列相关公式 递推方法 猜想归纳法 构造辅助数列 叠乘法chengcheng 法 观察法 数列求通项的一般方法 与的关系 利用 易漏n=1哟！‎ 用于型已知条件 ‎ ‎ ‎ 二、数列求和 ‎ 把一组需要求和的数列拆分成两组或两组以上的特殊数列来求和 把通项公式是分子为非零常数，分母为非常数列的等差数列的两项积的形式拆成两个分式差的形式之后再求和 倒序相加法 裂项相消法 错位相减法 分组求和法 主要是针对等差等比数列，直接应用求和公式 公 式 法 数列求和的一般方法（五种）‎ 若某数列中，与首末两项等距离的两相和等于首末两项和，可采用把正着写的和倒着写的两个式子相加，就得到一个与常数数列求和相关的式子 设数列的等比数列，数列是等差数列，求数列的前项和时，常常将的各项乘以的公比，并向后错一项与的同次项对应相减，即可转化为特殊数列求和 补充：‎ 典型例题 ‎ 一．通项 类型1：等差求通项思想：叠加求通项，用于型； ‎ 例1：（03全国19）已知数列||满足（I）求（II）证明：‎ 变式1：（08四川）设数列中，，，则通项 = ‎ 类型2：等比求通项思想：叠乘求通项，用于型； ‎ 例2：在数列中，则 变式1：设是首项为1的正项数列， 则它的通项公式是_____‎ 类型3： 已知求通项： ‎ 例3：（07福建21）数列的前项和为，，．（Ⅰ）求数列的通项；（Ⅱ）求数列的前项和．‎ 类型4：构造等比或等差数列（递归数列）‎ 类型一：用于型已知条件。转化方法：设，由km-m=b求出m的值，则数列是以为公比的等比数列；通过求出间接求出通项.‎ 类型二：用于型已知条件。‎ 转化步骤：（1）等式两边同时除以：；（2）令，则；‎ 当时，是以1为公差的等差数列；当时，转化为类型一构造等比数列；‎ 类型三：用于型已知条件。‎ 转化步骤：设，由求出：‎ ‎，则是以为公比，‎ 为首项的等比数列；通过求出间接求出通项.‎ 例4：（06重庆）在数列中，若，则该数列的通项___‎ 例5： （08全国19）在数列中，，．求数列的前项和．‎ 例6：（08全国19）在数列中，，．（Ⅰ）设．证明：数列是等差数列；（Ⅱ）求数列的前项和．‎ 小结：先证明新数列为等差或等比再求通项问题，先从问题入手按证明等差或等比方法证明问题，再由等差或等比的通项公式间接解决问题。‎ 类型5：分式型递归数列解决办法；‎ 解决步骤：（1）两边颠倒分子分母,得到：；（2）令，则 当时, 为等差数列；当时,转化为类型4中问题.‎ 例7：数列中，则 变式1：.(08陕西22)已知数列的首项，，．（Ⅰ）求的通项公式；‎ 类型6：指数型递归数列（两边取对数）如：：两边取对数得到：‎ ‎，令，则，则转化为类型4；‎ 例，数列满足： ，求的通项；‎ 类型8：递推思想（升标或降标法）：据已知条件推出类似等量关系后两式再作差（用于知与或与相邻项之间的关系）；‎ 例7： (04全国卷)若数列满足,则的通项.‎ 变式1：数列满足,则?‎ 综合练习：‎ ‎1．（05天津）在数列{an}中,a1=1,a2=2,且则=_____．‎ ‎2．（07江西）已知数列对于任意，有，若，则____‎ ‎3．（04全国19）数列{an}的前n项和记为Sn，已知a1＝1，an＋1＝Sn（n＝1，2，3，…）．证明(Ⅰ)数列{}是等比数列； (Ⅱ)Sn＋1＝4an．‎ ‎4.(08四川20)设数列的前项为，已知．‎ ‎（Ⅰ）证明：当时，是等比数列；（Ⅱ）求的通项公式．‎ ‎5．（09四川22）设数列的前项和为，对任意的正整数，都有成立，记.（I）求数列的通项公式；‎ ‎6. (07福建）等差数列的前项和为．（Ⅰ）求的通项与前项和；（Ⅱ）设，求证：数列中任不同的三项不可能成为等比数列；‎ ‎7.(07北京）数列中，，（是常数，），且成公比不为的等比数列．（I）求的值；（II）求的通项公式．‎ ‎8.(07山东）设是公比大于1的等比数列，为数列的前项和．已知，且构成等差数列．（1）求数列的通项公式．‎ ‎（2）令求数列的前项和．‎ ‎9．（06陕西) 已知正项数列{an}，其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列，求数列{an}的通项an .‎ 二．数列求和 例1：求下列数列的前项和： ‎ ‎ ‎ 变式：数列为等差数列，（1）求通项公式；‎ ‎（2），求数列前项和；‎ 小结求和方法： （1）公式法：用于等差与等比数列；‎ ‎（2）倒序相加法：若某数列中，与首末两项等距离的两相和等于首末两项和，可采用把正着写的和倒着写的两个式子相加，就得到一个与常数数列求和相关的式子 ‎（3）错位相减法：设数列的等比数列，数列是等差数列，则求数列的前项和时，常常将的各项乘以的公比，并向后错一项；‎ ‎（4）裂项相消法：把通项公式是分子为非零常数，分母为非常数列的等差数列的两项积的形式拆成两个分式差的形式之后再求和；‎ ‎， ‎ ‎（5）分组求和法：把一组需要求和的数列拆分成两组或两组以上的特殊数列来求和 练习：1．(07福建)数列的前项和为，若，则 ‎ ‎ ‎6．等差数列前3项之和为12，后3项之和为132，所有各项之和为240，则项数 ‎7．求前n项和