湖北省黄冈中学高考数学模拟试题 72页

湖北省黄冈中学高考数学模拟考试 1 数学试题（理科） 试卷类型：A 注意事项： 1．答题前，考生务必将自己的学校、班级、姓名、考号填写在试题卷封线内，将考号最后两位 填在答题卷右上方座位号内，同时机读卡上的项目填涂清楚，并认真阅读答题卷和机读卡 上的注意事项。 2．选择题每小题选出答案后，用 2B 铅笔把机读卡对应题目的答案标号涂黑；如需改动，用像 皮擦干净后，再选涂其它答案标号，答在试题卷上无效。 3．将填空题和解答题用 0．5 毫米黑色墨水签字笔或黑色墨水钢笔直接答在答题卷上每题对应 的答题区域内，答在试卷上无效。 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分，在每小题给出的四个选项中，只有一项是 满足题目要求的。 1．已知集合 ，若 ，则 等于　　　　　　（ 　 ） A． B． C． 或 　 D． 或 2．复数 满足 ，则 （ ） A． B． C． D． 3．已知函数 的定义域为[a,b]，值域为[-2，1]，则 b-a 的值不可能是 （ ） A. B. C. D. 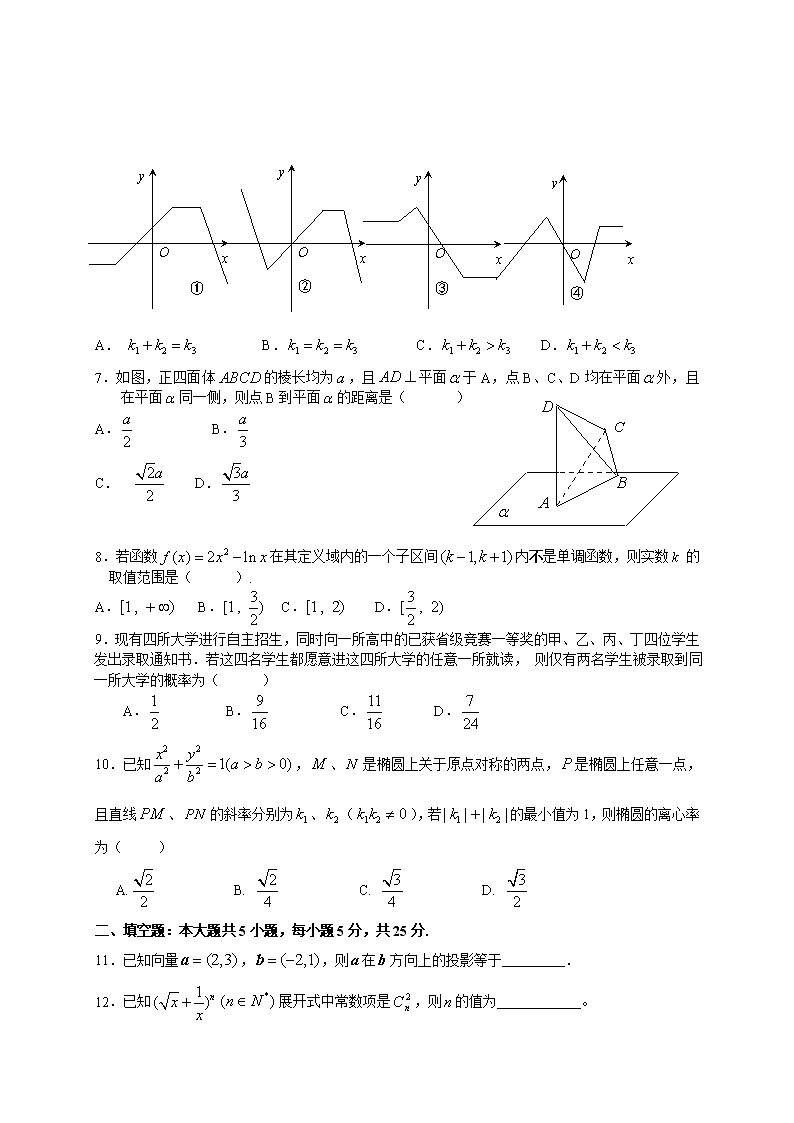4． 为互不相等的正数， ，则下列关系中可能成立的是（ ） A． B． C． D． 5． 设两个正态分布 和 曲线如图所示,则有 A． B． C． D． 6．下列四个函数图象，只有一个是符合 （其中 为正 实数， 为非零实数）的图象，则根据你所判断的图象， 之间一定成立的关系是 （ ） 2{0, }, { | 2 5 0, }P m Q x x x x Z= = − < ∈ P Q ≠ ∅ m 1 2 1 2 5 1 2 z ( 2)z z i= + z = 1 i+ 1 i− 1 i− + 1 i− − 2siny x= 6 5π π 6 7π π2 , ,a b c 2 2 2a c bc+ = a b c> > b a c> > a c b> > b c a> > 2 1 1 1( , )( 0)N µ σ σ > 2 2 2 2( , )( 0)N µ σ σ > 1 2 1 2,µ µ σ σ< > 1 2 1 2,µ µ σ σ< < 1 2 1 2,µ µ σ σ> > 1 2 1 2,µ µ σ σ> < 1 1 2 2 3 3| | | | | |y k x b k x b k x b= + + + − + 1 2 3, ,k k k 1 2 3, ,b b b 1 2 3, ,k k k x y 2 1 1( , )N µ σ 2 2 2( , )N µ σ A． B． C． D． 7．如图，正四面体 的棱长均为 ，且 平面 于 A，点 B、C、D 均在平面 外，且 在平面 同一侧，则点 B 到平面 的距离是（ ） A． B． C． D． 8．若函数 在其定义域内的一个子区间 内不是单调函数，则实数 k 的 取值范围是（ ）. A． B． C． D． 9．现有四所大学进行自主招生，同时向一所高中的已获省级竞赛一等奖的甲、乙、丙、丁四位学生 发出录取通知书．若这四名学生都愿意进这四所大学的任意一所就读， 则仅有两名学生被录取到同 一所大学的概率为（ ） A． B． C． D． 10．已知 ， 、 是椭圆上关于原点对称的两点， 是椭圆上任意一点， 且直线 、 的斜率分别为 、 （ ），若 的最小值为 1，则椭圆的离心率 为（ ） A. B. C. D. 二、填空题：本大题共 5 小题，每小题 5 分，共 25 分. 11．已知向量 ， ，则 在 方向上的投影等于 ． 12．已知 展开式中常数项是 ，则 的值为 　 。 1 2 3k k k+ = 1 2 3k k k= = 1 2 3k k k+ > 1 2 3k k k+ < ABCD a AD ⊥ α α α α 2 a 3 a 2 2 a 3 3 a 2( ) 2 lnf x x x= − ( 1, 1)k k− + [1, )+ ∞ 3[1, )2 [1, 2) 3[ , 2)2 1 2 9 16 11 16 7 24 2 2 2 2 1( 0)x y a ba b + = > > M N P PM PN 1k 2k 1 2 0k k ≠ 1 2| | | |k k+ 2 2 2 4 3 4 3 2 (2,3)=a ( 2,1)= −b a b 1( )nx x + )( *Nn ∈ 2 nC n α A B C D x y O x y O x y Ox y O ① ② ③ ④ 13．在等比数列 中，若 ， ，则 　 　 。 14． ， ， ，当 取得最大值时， ， ，则实数 的取值范围是 。 15．设函数 的定义域为 D，若存在非零实数 使得对于任意 ，有 ， 且 ，则称 为 M 上的 高调函数。 如果定义域为 的函数 为 上的 高调函数，那么实数 的取值范围 是 。如果定义域为 R 的函数 是奇函数，当 时， ，且 为 R 上的 4 高调函数，那么实数 的取值范围是 。 三、解答题：本大题共 6 小题，共 75 分。解答应写出文字说明、证明过程或演算步骤。 16．（本小题满分 12 分）已知 中， 、 、 是三个内角 、 、 的对边，关于 的不 等式 的解集是空集． （1）求角 的最大值； （2）若 ， 的面积 ，求当角 取最大值时 的值． 17． (本小题满分 12 分)某公司有 10 万元资金用于投资，如果投资甲项目，根据市场分析知道：一 年后可能获利 10﹪，可能损失 10﹪，可能不赔不赚，这三种情况发生的概率分别为 ， ， ；如果投资乙项目，一年后可能获利 20﹪，也可能损失 20﹪，这两种情况发生的概率分别为 . （1）如果把 10 万元投资甲项目，用 表示投资收益（收益=回收资金－投资资金）， 求 的概率分布及 ； （2）若把 10 万元投资投资乙项目的平均收益不低于投资甲项目的平均收益，求 的取值范围. { }na 7 8 9 10 15 8a a a a+ + + = 8 9 9 8a a = − 7 8 9 10 1 1 1 1 a a a a + + + = 0 ( , ) | 0 5 0 y M x y x x y  ≥    = ≥     + − ≤  ( , ) | 3 5 0 y t N x y x x y  ≤    = ≤     + − ≥  ( , )x y M N∈  2x y+ ( , )x y N∈ ( , )x y M∉ t ( )f x l ( )x M M D∈ ⊆ x l D+ ∈ ( ) ( )f x l f x+ ≥ ( )f x l [ 1, )− +∞ 2( )f x x= [ 1, )− +∞ m m ( )f x 0x ≥ 2 2( ) | |f x x a a= − − ( )f x a ABC∆ a b c A B C x 2 cos 4 sin 6 0x C x C+ + < C 7 2c = ABC∆ 3 32S = C a b+ 2 1 4 1 4 1 ）（和 1=+ βαβα ξ ξ ξE α 18．（本小题满分 12 分） 在四棱锥 中，侧面 底面 ， ， 为 中点，底面 是直角梯形， ， =90°, ， . （1）求证： 平面 ； （2）求证： 平面 ； （3）设 为侧棱 上一点， ， 试确定 的值，使得二面角 为 45°. 19． (本小题满分 12 分)已知函数 f(x)= (1)当 时, 求 的最大值; (2) 设 , 是 图象上不同两点的连线的斜率，否存在实数 ，使得 恒成立?若存在,求 的取值范围;若不存在,请说明理由． 20．（本小题满分 13 分）在平面直角坐标系 中，线段 AB 与 y 轴交于点 ，直线 AB 的斜 率为 k，且满足 ． （1）证明：对任意的实数 ，一定存在以 y 轴为对称轴且经过 A、B、O 三点的抛物线 C，并求出抛 物线 C 的方程； （2）对（1）中的抛物线 C，若直线 与其交于 M、N 两点，求 ∠MON 的取值范围． 21． (本小题满分 14 分) 设数列 的前 项和为 ，已知 (n∈N*). （1）求数列 的通项公式； （2）设 ，数列 的前 项和为 ，若存在整数 ，使对任意 n∈N*且 n≥2，都有 成立，求 的最大值； （3）令 ，数列 的前 项和为 ，求证：当 n∈N*且 n≥2 时， . xOy )2 1,0(F )0(: >+= mmxyl P ABCD− PCD ⊥ ABCD PD CD⊥ E PC ABCD //AB CD ADC∠ 1AB AD PD= = = 2CD = BE // PAD BC ⊥ PBD Q PC PQ PCλ=  λ Q BD P− − 2 1ln , [ , 2]2 a x x a R xx −  + ∈ ∈   1[ 2, )4a∈ − ( )f x 2( ) [ ( ) ln ]g x f x x x= − ⋅ k ( )g x a 1k < a 2| | | | 1AF BF k× = + k { }na n nS 12 2n n nS a += − { }na 1 log 2nn a n b + = { }nb n nB m 3 20n n mB B− > m 1 1 ( 1) log 2n n n a n c + + = − { }nc n nT 2 2 2nT < A P B C E D 参考答案 理科 B ： 答案 1—5 CBCAB 6—10 BDCDA １．D【解析】 ，因为 ，故 或 。 2． C【解析】 3. D 【解析】值域[-2,1]含最小值不含最大值,故定义域小于一个周期,故选 D 4． B 【解析】若 ，则 ，不合条件，排除 ， 又由 ，故 与 同号，排除 ；且当 时， 有可能成立，例如取 ，故选 ． 5． A【解析】显然 ，正态曲线越“瘦高”，表示取值越集中， 越小。 6． A【解析】当 足够小时 当 足够大时 可见，折线的两端的斜率必定为相反数，此时只有③符合条件。此时 7．A【解析】取 AD 的中点 M，易证 平面 ，故平面 平面 ，平面 到平面 的距离为 ，即为 B 到平面 的距离。 8． B【解析】因为 定义域为 ，又 ，由 ，得 . 据题意， ，解得 9．B【解析】所有等可能的结果相当于甲、乙、丙、丁四位学生任选四所大学之一，共有 种，仅 有两名学生被录取到同一所大学，可先把四个同学分成 1+1+2 三份，有 种分法，再选择三所大学 就读，即有 种就读方式。故所求的概率为 。 10 ． D 【 解 析 】 设 ， ， ， 可 得 ， ， }2,1{},2 50|{ =∈<<= ZxxxQ P Q φ≠ 1m = 2 2 11 iz ii = = − +− a b> 2 2 2 2 2a c b c bc+ > + ≥ ,A D ( )2 2 2a c c b c− = − a c− b c− B b a c> > 2 2 2a c bc+ = ( ) ( ), , 3,5,1a b c = C 1 2 µ µ< σ x 1 2 3 1 2 3( ) ( )y k k k x b b b= − + − − + − x 1 2 3 1 2 3( ) ( )y k k k x b b b= + − + + − 1 2 3 0k k k+ − = AD ⊥ BCM BCM / / α BCM α 2 a α ( )f x (0, )+∞ 1( ) 4f x x x ′ = − ( ) 0f x′ = 1 2x = 11 12 1 0 k k k  − < < +  − ≥ 31 .2k≤ < 44 2 4C 2 3 4 4C A 2 3 4 4 4 9 4 16 C A = ( cos , sin )M a bα α ( cos , sin )N a bα α− − ( cos , sin )P a bβ β 1 2 (sin sin ) (sin sin ),(cos cos ) (cos cos ) b bk ka a β α β α β α β α − += =− + 2 2 2 2 1 2 2 2 2 2 (sin sin )| | | | | |(cos cos ) b bk k a a β α β α −⋅ = =− ∴ 。 11． 【解析】 在 方向上的投影为 ． 12． 3 或 6【解析】展开式的通项为 ，若要其表示常数项，须有 ，即 ，又由题设知 ， 或 ， 或 . 13． 【解析】 14． 【解析】如图，M、N 表示的区域如图所示， 显然最优解在 C 处取得，过 A 作斜率为-2 的直线交直 线 BC 于 F，则 C 应在点 F 上方，可求得 F（3，4）， ∴ 。 15． 【解析】∵ ， ，即 ， 的图象如图， ∴ 。 16．解：（1）显然 不合题意， 则有 ，即 ， 即 ， 1 2 1 2 2 2 3| | | | 2 | | 1 2 b bk k k k ea a + ≥ = ⇒ = ⇒ = 5 5 − a b 5cos , 5 = = = − a b a ba a b a a b b 1 3 12 2 1 ( ) ( ) n r r n r r r r n nT C x x C x − − − + = = 3 02 n r- = 1 3r n= 1 2 3n n nC C= 12 3 n = 12 3n n- = 6n = 3n = 5 3 − 7 10 8 9 7 8 9 10 7 10 8 9 7 10 8 9 1 1 1 1 1 1 1 1( ) ( ) a a a a a a a a a a a a a a a a + ++ + + = + + + = + 7 8 9 10 8 9 5 3 a a a a a a + + += = − 4t > 4t > 2; 1 1m a≥ − ≤ ≤ ( 1) (1)f f− = 1 ( 1)m ≥ − − 2m ≥ 2 2( ) | |f x x a a= − − 2 24 3 ( ) 1 1a a a≥ − − ⇒ − ≤ ≤ 0cos =C cos 0 0 C > ∆ ≤ 2 cos 0 16sin 24cos 0 C C C >  − ≤ cos 0 1cos 2 cos 2 C C C > ≤ − ≥ 或 y O x2a 22a 23a2a− C F D E O A B x y N M 故 ，∴角 的最大值为 。………………………………………………6 分 （2）当 = 时， ，∴ ，…………………8 分 由余弦定理得 ， ∴ ，∴ 。…………………………………………12 分 17．解：（1）依题意， 的可能取值为 1，0，－1 的分布列为 1 0 p = = ……………………………………6 分 （2）设 表示 10 万元投资乙项目的收益，则 的分布列为 2 p 依题意要求 ………………12 分 18．解：（1）取 PD 的中点 F，连结 EF， AF，因为 E 为 PC 中点，所以 EF//CD， 且 在梯形 ABCD 中，AB//CD，AB=1， 所以 EF//AB，EF=AB， 四边形 ABEF 为平行四边形， 所以 BE//AF， ………2 分 BE 平面 PAD，AF 平面 PAD， 所以 BE//平面 PAD.…………4 分 （2）平面 PCD⊥底面 ABCD，PD⊥CD，所以 PD⊥平面 ABCD， 所以 PD⊥AD. 如图，以 D 为原点建立空间直角坐标系 D—xyz. 则 A（1，0，0），B（1，1，0），C（0，2，0），P（0，0，1） …………6 分 1cos 2C ≥ C 60° C 60° 1 3 3sin 32 4 2ABCS ab C ab∆ = = = 6ab = 2 2 2 22 cos ( ) 2 2 cosc a b ab C a b ab ab C= + − = + − − 2 2 121( ) 3 4a b c ab+ = + = 11 2a b+ = ξ ξ ξ 1− 2 1 4 1 4 1 ξE 2 1 4 1− 4 1 η η η 2− α β 2422 −=−= αβαηE 1 94 2 ,14 16 α α− ≥ ≥ ,12 1 == CDEF ⊄ ⊂ ).0,1,1(),0,1,1( −== BCDB A P B C E D Q F y z x 所以 又由 PD⊥平面 ABCD，可得 PD⊥BC， 所以 BC⊥平面 PBD.………………………8 分 （3）平面 PBD 的法向量为 ，所以 ， 设平面 QBD 的法向量为 n=（a，b，c）， ， 由 n ，n ，得 所以， 所以 n= ……………………10 分 所以 注意到 ，得 ………………12 分 19． (1)当-2≤ < 时，由 =0 得 x1= ………………2 分 显然-1≤x1< , = aayxC 02 2 =−− aakxx ),(),,( BBAA yxByxA 2 axx BA −=⋅ ||1|0|1|| 22 AA xkxkAF +=−+= ||1|0|1|| 22 BB xkxkBF +=−+= 2)1(|2|)1(||)1(|||| 222 akakxxkBFAF BA +=+=⋅+=⋅ 21|||| kBFAF +=⋅ 2=a yxC 2: 2 = ),(),,( NNMM yxNyxM    = += yx mxy 22 0222 =−−⇒ mxx 084 >+=∆ m )0( >m 2=+ NM xx mxx NM 2−=⋅ M OM x mk += 1 N ON x mk += 1 NM xx < 0>m NM xx << 0 2 πθ ≠=∠MON θ 3 3 2 21 2 1 2 2 1 1 1 2 2 1 2 1 2 ( ) ( ) ( )y y a x x x xk a x x x xx x x x − − + −= = = − + +− − 1k < a < 2 2 1 1 2 2( )x x x x+ + 2 2 1 44 x≤ ≤ 7 4a ≤ 7( , )4a∈ −∞ ( )y g x= 0 0( , )P x y 21 2 0 0 1 2 ( ) ( ) '( ) 3 1g x g xk g x a xx x −= = = − <− 2 0 71 3 4a x∴ < + ≤ 7( , )4a∈ −∞ ……………………………9 分 令 ，则 ， 且 ∴ 函数 与 在 上皆为增函数 ∴ ∴ ……………………11 分 则 ， 又 时， ∴ ………………………………………13 分 21.（1）由 ，得 (n≥2). 两式相减，得 ，即 (n≥2). 于是 ，所以数列 是公差为 1 的等差数列. ……………2 分 又 ，所以 . 所以 ，故 . ……………4 分 （2）因为 ，则 . 令 ，则 . 所以 . 即 ，所以数列 为递增数列. …………7 分 所以当 n≥2 时， 的最小值为 . 据题意， ，即 .又 为整数，故 的最大值为 18. ……………8 分 （3）因为 ，则当 n≥2 时， )2(2 212 1tan ≠− +=⋅+ −= mm m kk kk ONOM ONOMθ mt 21+= 2 12 −= tm 1>t 5≠t ttt t 5 4 5 4tan 2 −+ =−=θ xy = xy 5−= ),0( +∞ −t ),0()0,4(5 +∞∪−∈ t ),0()1,(5 4 +∞∪−−∞∈−+ tt )4 3,2()2,0( πππθ ∪∈ 2=m 2 πθ ==∠MON )4 3,0( π∈∠MON 12 2n n nS a += − 1 12 2n n nS a− −= − 12 2 2n n n na a a −= − − 12 2n n na a −− = 1 1 12 2 n n n n a a − −− = { }2 n n a 2 1 12 2S a= − 1 4a = 2 ( 1) 12 n n a n n= + − = + ( 1) 2n na n= + ⋅ 2 1 log 2 log 2nnn a n b + = = 1 n = 3 1 1 1 1 2 3n nB B n n n − = + + ++ +  1 1 1( ) 1 2 3f n n n n = + + ++ +  1 1 1 1 1 1( 1) 2 3 3 3 1 3 2 3 3f n n n n n n n + = + + + + + ++ + + + + 1 1 1 1( 1) ( ) 3 1 3 2 3 3 1f n f n n n n n + − = + + −+ + + + 1 1 2 1 1 2 03 1 3 2 3 3 3 3 3 3 3 3n n n n n n = + − > + − =+ + + + + + ( 1) ( )f n f n+ > { }( )f n ( )f n 1 1 1 1 19(2) 3 4 5 6 20f = + + + = 19 20 20 m < 19m < m m 1 1( 1)n nc n += − ⋅ . ……………9 分 下面证 方法一：先证一个不等式，当 时， 令 ，则 ， ∴ 在 时单调递增， ，即当 时， 令 ， ， ， ， ，……， 以上 个式相加，即有 ∴ ……………14 分 方法二：先用数学归纳法证明一个加强不等式 。 ① 时， 成立，故 时不等式成立。 ②假设 时成立，即 则当 时， ，下面用分析法证 即证 即证 ， 故即证 ，即证 上式显然成立。 （可以从 到 时引导学生发现 中的 的值，此 2 1 1 1 1 11 2 3 4 2 1 2nT n n = − + − + + −− 1 1 1 1 1 1(1 ) 2( )2 3 2 2 4 2n n = + + + + − + + +  1 1 1 1 2 2n n n = + + ++ +  1 1 1 2 1 2 2 2n n n + + + <+ +  0x > ln( 1) 1 xx x + > + ( ) ln( 1) ( 0)1 xg x x xx = + − >+ 2 2 1 1'( ) 01 ( 1) ( 1) xg x x x x = − = >+ + + ( )g x (0, )+∞ ( ) (0) 0g x g> = 0x > ln( 1) 1 xx x + > + 1x n = 1 1 1ln ln( 1) ln1 1 n n nn n n + > ⇒ + − >+ + 1ln( 2) ln( 1) 2n n n + − + > + 1ln( 3) ln( 2) 3n n n + − + > + 1ln(2 ) ln(2 1) 2n n n − − > n 1 1 1ln(2 ) ln 1 2 2n n n n n − > + + ++ +  1 1 1 2ln(2 ) ln ln 21 2 2 2n nn n n + + + < − = <+ +  1 1 1 2 1 1 2 2 2 4 1n n n n + + + < −+ + + 2n = 1 1 2 1 3 4 2 9 + < − 2n = n k= 1 1 1 2 1 1 2 2 2 4 1k k k k + + + < −+ + + 1n k= + 1 1 1 1 2 1 1 1 1 2 2 2 1 2 2 2 4 1 2 1 2 2 1k k k k k k k k + + + + < − + + −+ + + + + + + 2 1 1 1 2 4 1 2 1 2 2k k k = − + −+ + + 2 1 1 1 2 1 2 4 1 2 1 2 2 2 4 5k k k k − + − < −+ + + + 1 1 1 1 4 1 1 52 1 2 2 4 1 4 5 (4 1)(4 5) (2 )(2 )2 2 k k k k k k k k − < − = =+ + + + + + + + 1 1 1 5(2 1)(2 2) (2 )(2 )2 2 k k k k <+ + + + 1 5(2 1)(2 2) (2 )(2 )2 2k k k k+ + > + + 2 2 54 6 2 4 6 4k k k k+ + > + + n = k 1n k= + 1 1 1 2 1 1 2 2 2 ( )k k k g n + + + < −+ +  ( )g n 种方法对于常数型的关于正整数的不等式的证明很凑效） 方法三：又据柯西不等式，有 . 故 . ……………14 分 湖北省黄冈中学高考数学模拟考试 2 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．卷面共 150 分，考试时间 120 分 第Ⅰ卷 （选择题 共 50 分） 一、选择题：本大题共 10 小题，每题 5 分，共 50 分．在每小题给出的四个选项中，只有一项是符 合题目要求的． 1.设 是集合 A 到集合 B 的映射．若 ，则 （ ） A．{0, ３} B．{0}　 C．{3}　　 D．{ ，0} 2.函数 的图像大致是（ ） 3.“a = 3”是“直线 与直线 平行”的（ ）条件 A．充分而不必要 B．必要而不充分 C．充要 D．既不充分也不必要 4．某校为了了解高三学生的身体状况，抽取了 100 名女生 的体重.将所得的数据整理后，画出了如图的频率分布直 方图，则所抽取的女生中体重在 45~50kg 的人数是( ) A．10 B．30 C．50 D．60　 2 2 2 2 2 2 1 1 1 1 1 1(1 1 1 )[ ]1 2 2 ( 1) ( 2) (2 )n n n n n n + + + < + + + + + ++ + + +   1 1 1[ ]( 1) ( 1)( 2) (2 1)(2 )n n n n n n n < + + ++ + + − 1 1 2( )2 2n n n = − = 2 2 2nT < f x x→： { }3 0 3A = − ， ， A B = 3− 2|log |( ) 2 xf x = 2 1 0ax y− − = 6 4 0x y c− + = 40 45 50 55 60 体重 频率 组距 （kg） 0.10 0.08 0.06 0.04 0.02 A B DC y O x1− 1 1 y O x1− 1 1 y O x1− 1 y O x1− 1 1 5. 若 ， 且 ， 则 向 量 与 的 夹 角 为 ( ) (4 题图) A．30° B．60° C．150° D．120°　 6. 给出四个函数，则同时具有以下两个性质：①最小正周期是 ； ②图象关于点（ ，0)对称 的函数是（ ） A. B. C. D. 7．从 4 名男生和 3 名女生中选出 3 人，分别从事三项不同的工作，若这 3 人中至少有一名女生,则 选派方案共有( )种 Ａ. 108 Ｂ. 186 Ｃ. 216 Ｄ. 270 8．已知球面的三个大圆所在平面两两垂直，则以三个大圆的交点为顶点的八面体的体积与球体积 之比是（ ） A. 1∶π B. 1∶2π C. 2∶π D. 4∶3π 9.已知⊙ ，⊙ ，两圆的内公切线交于 点，外公切线交于 点，则 分 的比为( ) A. B. C. D. 10.若 表示实数 中的最大者．设 ， ，记 设 ， ，若 ，则 的取值范围为（ ） A． B． C． D． 第 II 卷 （共 100 分） 二、填空题：本大题共 5 小题，每题 5 分，共 25 分． 11. 在 展开式所得的 x 的多项式中，系数为有理数的项有__________项． 12. 函数 ，则 ________________． | | 1,| | 2,a b c a b= = = +     c a⊥  a b π 6 π },,,max{ 21 nsss  nsss ,,, 21  ),,( 321 aaaA =           = 3 2 1 b b b B }.,,max{ 332211 bababaBA =⊗ ,1( −= xA )1,1+x           − −= |1| 2 1 x xB 1−=⊗ xBA x ]1,31[ − ]21,1[ + ]1,21[ − ]31,1[ + sin( ) ( 1 0)( ) 3 ( 1) ( 0) x xf x f x x π − ≤ <=   − ≥ (1)f = 13. 甲乙两人进行乒乓球比赛,比赛规则为:３局２胜,即以先赢２局者为胜.根据经验,每局比赛中甲 获胜的概率为 0.6,则本次比赛甲获胜的概率为 。 14. x、y 满足约束条件： ，则 的最小值是______________． 15. 数列 的前 项和为 ，若数列 的各项按如下规律排列： ， ， ， ， ， ， ， ， ， ，…， ， ，…， ，…有如下运算和结论： ① ； ② ； ③数列 ， ， ， ，…是等比数列 ④数列 ， ， ， ，…的前 项和为 ； ⑤若存在正整数 ，使 ， ，则 . 在后面横线上填写出所有你认为正确运算结果或结论的序号______________． 三、解答题：本题共 6 小题，共 75 分，解答应写出文字说明、证明过程或演算步骤． 16.（本小题满分 12 分） 已知 （1）求函数 的最小正周期； （2）当 的最大值及最小值。 17.（本小题满分 12 分） 如图，已知四棱锥 中， ⊥平面 ， 是直角梯形， ， 90º， ． （1）求证： ⊥ ； （2）在线段 上是否存在一点 ，使 //平面 ， 若存在，指出点 的位置并加以证明；若不存在，请说明理由 2 2 5 0 4 0 y x y x y ≥  + − ≥  + − ≤ 5z x y= + − { }na n nS { }na 1 2 1 3 2 3 1 4 2 4 3 4 1 5 2 5 3 5 4 5 1 n 2 n 1n n − 23 3 8a = 11 11 6S = 1a 2 3a a+ 4 5 6a a a+ + 7 8 9 10a a a a+ + + 1a 2 3a a+ 4 5 6a a a+ + 7 8 9 10a a a a+ + + n 2 4n n nT += k 10kS < 1 10kS + > 5 7ka = .)(),cos2,sin(cos),sin,sin(cos baxfxxxbxxxa ⋅=−=+= 设 )(xf )(]2,0[ xfx 时，求函数π∈ ABCDP − PA ABCD ABCD BCAD // BAD∠ = ADBC 2= AB PD PB E AE PCD E A C D B P 18．（本小题满分 12 分） 已 知 数 列 是 首 项 为 ， 公 比 的 等 比 数 列 ， 设 , ( ) （1）求数列 的通项公式； （2）求数列 的前 n 项和 Sn. 19．（本小题满分 13 分）某企业投入 81 万元经销某产品，经销时间共 60 个月，市场调研表明，该 企业在经销这个产品期间第 个月的利润 （单位：万元），为了获得 更 多 的 利 润 ， 企 业 将 每 月 获 得 的 利 润 投 入 到 次 月 的 经 营 中 ， 记 第 个 月 的 当 月 利 润 率 ，例如： ． （1）求 ； （2）求第 个月的当月利润率 ； （3）该企业经销此产品期间，哪个月的当月利润率最大，并求该月的当月利润率． 20．（本题满分 12 分） 已知函数 的图象为曲线 C。 （1）若曲线 C 上存在点 P，使曲线 C 在 P 点处的切线与 轴平行，求 的关系； （2）若函数 时取得极值，求此时 的值； （3）在满足（2）的条件下， 的取值范围。 21 （ 14 分 ） 设 是 椭 圆 的 两 点 ， ， { }na 1 1 4a = 1 4q = *)(log32 4 1 Nnab nn ∈=+ nnn bac = *Nn∈ }{ nb }{ nc x * * 1 (1 20, ) ( ) 1 (21 60,10  ≤ ≤ ∈= ≤ ≤ ∈ ） x x N f x x x x N x ( ) xg x x = 第 个月的利润 第 个月前的资金总和 (3)(3) 81 (1) (2) fg f f = + + (10)g x ( )g x cbxaxxxf ++−= 23)( x ,a b 31)( =−= xxxf 和可以在 ,a b cxcxf 求恒成立在 ,]6,2[2)( −∈< ( ) ( )1 1 2 2, , ,A x y B x y ( )2 2 2 2 1 0y x a ba b + = > > 1 1,x ym b a  =     F E A D B C P F E A D B C P ，且 ，椭圆离心率 ，短轴长为 2，O 为坐标原点。 （1）求椭圆方程； （2）若存在斜率为 的直线 AB 过椭圆的焦点 （ 为半焦距），求 的值； （3）试问 的面积是否为定值？若是，求出该定值；若不是，说明理由。 试 题 答 案 一、选择题：本大题共 10 小题，每题 5 分，共 50 分． 1．Ａ 2．C 3．B 4．Ｃ 5．Ｄ 6．D 7．B 8．A 9．C 10．Ｂ 二、填空题：本大题共 5 小题，每题 5 分，共 25 分． 11．17 12． 13. 0.648 14． 15．②④⑤ 三、解答题：本题共 6 小题，共 75 分． 16.解：（1） （2） …………8 分 17.证明：（1）∵ ⊥平面 ， 平面 ， ∴ ⊥ . ………… 2 分 ∵ ⊥ ， ， ∴ ⊥平面 ，………… 5 分 ∵ 平面 ， ∴ ⊥ . ………… 6 分 （2）[法 1]: 取线段 的中点 ， 的中点 ，连结 , 则 是△ 中位线. ∴ ∥ ， ， ∵ ， ， 2 2,x yn b a  =     0m n⋅ =  3 2e = k ( )0,F c c k AOB∆ 3 2 − 3 2 − xxxxxxbaxf cos2sin)sin(cos)sin(cos)( ⋅+−⋅+=⋅= 分的最小正周期 分 分 分 6.)( 5)42sin(2)2sin4cos2cos4(sin2 3)2sin2 22cos2 2(22sin2cos 2cossin2sincos 22     π πππ =∴ +=+= +=+= +−= Txf xxx xxxx xxxx .4 5 424,20 ππππ ≤+≤∴≤≤ xx 分有最小值时即当 分有最大值时即当 12.1)(,2,4 5 42 10.2)(,8,242   −==+ ==+∴ xfxx xfxx πππ πππ PA ABCD AB ⊂ ABCD PA AB AB AD PA  AD A= AB PAD PD ⊂ PAD AB PD PB E PC F DFEFAE ,, EF PBC EF BC BCEF 2 1= BCAD // BCAD 2 1= ∴ . ∴ 四边形 是平行四边形， ………… 8 分 ∴ . ∵ 平面 ， 平面 ，………… 10 分 ∴ ∥平面 . …………11 分 ∴ 线段 的中点 是符合题意要求的点． ………… 12 分 [法 2]: 取线段 的中点 ， 的中点 ，连结 , 则 是△ 的中位线. ∴ ∥ ， ， ∵ 平面 , 平面 , ∴ 平面 . ∵ ， ， ∴ . ∴ 四边形 是平行四边形， ………… 8 分 ∴ . ∵ 平面 ， 平面 ， ∴ ∥平面 . ∵ , ∴平面 平面 . ………… 10 分 ∵ 平面 , ∴ ∥平面 . ………… 11 分 ∴ 线段 的中点 是符合题意要求的点．………… 12 分 18．解:（1）由题意知， ，……………2 分 又 ， 故 ……………4 分 （2）由（1）知， ……………6 分 ……7 分 …9 分 两式相减，得 …12 分 ……………12 分 BC EFADEFAD =,// EFDA DFAE // AE ⊄ PCD DF ⊂ PCD AE PCD PB E PB E F AFEFAE ,, EF PBC EF PC BCCF 2 1= ⊄EF PCD ⊂PC PCD //EF PCD BCAD // BCAD 2 1= CFADCFAD =,// DAFC CDAF // AF ⊄ PCD CD ⊂ PCD AF PDC FEFAF = //AEF PCD ⊂AE AEF AE PCD PB E *)()4 1( Nna n n ∈= 1 4 3log 2n nb a= − 3 2( *)nb n n N= − ∈ *)(23,)4 1( Nnnba n n n ∈−== *)(,)4 1()23( Nnnc n n ∈×−=∴ ,)4 1()23()4 1)53()4 1(7)4 1(44 11 132 nn n nnS ×−+(×−++×+×+×=∴ −  ∴ 1432 )4 1()23()4 1)53()4 1(7)4 1(4)4 1(14 1 +×−+(×−++×+×+×= nn n nnS  132 )4 1()23(])4 1()4 1()4 1[(34 1 4 3 +×−−++++= nn n nS  .)4 1()23(2 1 1+×+−= nn 2 3 2 1( ) ( *)3 3 4 n n nS n N +∴ = − × ∈ 19．解:（1）由题意得 ∴ ． …………………………2 分 （2）当 时， ∴ ．----------4 分 当 时， ∴当第 个月的当月利润率为 ……………………8 分 （4）当 时， 是减函数， 此时 的最大值为 ---10 分 当 时， 当且仅当 时，即 时， ，又 ， ∴当 时， ………………………………………………12 分 答：该企业经销此产品期间，第 40 个月的当月利润率最大，最大值为 …13 分 20．（1） ，…………1 分 (1) (2) (3) (9) (10) 1f f f f f= = = = = = (10) 1(10) 81 (1) (9) 90 = =+ + + fg f f 1 20x≤ ≤ (1) (2) ( 1) ( ) 1f f f x f x= = = − = = ( ) 1 1( ) 81 (1) ( 1) 81 1 80 = = =+ + + − + − + f xg x f f x x x 21 60x≤ ≤ 2 ( )( ) 81 (1) (20) (21) ( 1) 1 10 81 20 (21) ( 1) 1 210 ( 21)( 20) 1600101 20 f xg x f f f f x x f f x x x x x x x = + + + + + + − = + + + + − = =− + − ++    x * * 2 1 (1 20, )80( ) 2 (21 60,1600  ≤ ≤ ∈ +=   ≤ ≤ ∈ − + ） x x Nxg x x x x Nx x 1 20x≤ ≤ 1( ) 80g x x = + ( )g x 1(1) 81g = 21 60x≤ ≤ 2 2 2 2 2( ) 16001600 792 1600 11 xg x x x x x = = ≤ =− + −+ − 1600x x = 40x = max 2( ) 79g x = 2 1 79 81 > 40x = max 2( ) 79g x = 2 79 ),(,22)( 00 2 yxPbaxxxf 设切点为+−=′ （2）若函数 处取得极值， （3）由（2）得 根据题意， ２１.解(1)由 解得 所求椭圆方程为 ……３分 (2)设 AB 方程为 由 . ……………………………………………………5 分 由已知: = 解得 　　　　　　　　　　　……………………………………………………８分 (3)当 A 为顶点时,B 必为顶点,则 ,当 A,B 不为顶点时,设 AB 方程为 由 　 　 ， . 2 0 0 0 2 0 0 0 2 2 ( ) ( ) 3 2 ( ) 3 2 0 , 1 4 12 0, 3 3 y f x P k f x x ax b f x x ax b a b a b ′= = = − + ′ = − + = ∴∆ = − ≥ ≥   则曲线 在点 的切线的斜率 由题意知 有解 分 即 分 31)( =−= xxxf 和可以在 2 2( ) 3 2 1 3, 3 , 3, 9 7 f x x ax b x x a b a b ′ = − + = − = ≥ = = −  则 有两个解 和 且满足 易得 分 cxxxxf +−−= 93)( 23 3 2 3 2 3 2 3 9 ( [ 2,6]) 8 ( ) 3 9 ( [ 2,6]) 1 5( ), (6) 54, ( 2) 2 11 ( ) 3 9 ( [ 2,6]) 54, 54. 12 c x x x x g x x x x x x g g g x x x x x c > − − ∈ − = − − ∈ − = − = − = − ∴ = − − ∈ − >     恒成立 分 函数 在 时有极大值 用求导的方法 且 分 函数 的最大值为 所以 分 3 ,2 1 ce a b  = =  = 2, 1.a b= = ∴ 2 2 1.4 y x+ = .y=kx+ 3 2 2 3 14 y kx y x  = + + = ⇒ ( ) 24 2 3 1 0x kx+ + − =2k 1 2 2 2 3 ,4 kx x k −+ = + 1 2 2 1 4x x k −⋅ = + ( )( )1 2 1 2 1 2 1 22 2 10 3 34 x x y ym n x x kx kxb a = = + = + + +   2 2 2 4 1 3 2 3 3.4 4 44 4 k kkk k + − ⋅ − + ⋅ + + +  2.k = ± AOBS 1∆ = .y=kx+m 2 2 14 y kx m y x = + + = ⇒ ( ) 2 24 2 4 0x kmx m+ + + − =2k 1 2 2 2 ,4 mkx x k −+ = + 2 1 2 2 4 4 mx x k −⋅ = + 又 ,即 ,知 ,　　　……………11 分 = = = =1 三角形的面积为定值 1.　　　　　　…………………………………………………14 分 湖北省黄冈中学高考数学模拟考试 3 一、选择题：本小题共 10 小题，每小题 5 分，共 50 分，在每小题所给的四个 选项中，只有一项 是符合题目要求的。 1．已知复数 若 为实数，则实数 的值为( ) A． B． C． D． 2．记函数 的反函数为 ，若 ，则 的最小值是（ ） A． B． C． D． 3．已知 是两条不同的直线， 是两个不同的平面，有下列命题： ①若 ，则 ； ②若 ， ，则 ； ③若 ，则 ； ④若 ，则 ； 其中真命题的个数是( ) A．1 个 B．2 个 C．3 个 D．4 个 4．已知“命题 ”是“命题 ”成立的必要不充分条件，则 实数 的取值范围为（ ） A． B． C． D． 5．定义行列式运算： 将函数 的图象向左平移 个单位 ，若所得图象对应的函数为偶函数，则 的最小值是( ) A． B． C． D． 6．设集合 ，分别从集合 和 中随机取一个数 和 ，确定平面上的 一个点 ，记“点 落在直线 上”为事件 ，若事 1( ) 2xf x += 1( )f x− 1 1( ) ( ) 0f a f b− −+ = a b+ 1 2 2 2 4 2:( ) 3( )p x m x m− > − 2: 3 4 0q x x+ − < m 1 7m m> < −或 1 7m m≥ ≤ −或 7 1m− < < 7 1m− ≤ ≤ 0m n =   ( )( )1 2 1 2 1 04x x kx m kx m+ + + = 2 22 4m k− = AOB 1 2 1S 2 m x x∆ = ⋅ − ( )2 1 2 1 2 1 42 m x x x x⋅ + − 2 2 2 4 4 16 4 m k m k ⋅ − + + 24 2 m m ∴ 1 22 , 3 4 ,z m i z i= + = − 1 2 z z m 8 3 3 2 8 3 − 3 2 − m n、 α β、 , //m nα α⊂ //m n //m α //m β //α β ,m m nα⊥ ⊥ αn ,m mα β⊥ ⊥ //α β ,3241 43 21 aaaaaa aa −= 3 cos( ) 1 sin xf x x = m ( 0)m > m 3 2π 3 π 8 π π 6 5 {0,1 2,3} {0,1 2 3}A B= =， ， ，， A B a b ( )P a b， ( )P a b， x y n+ = (0 6 )nC n n N≤ ≤ ∈， 件 的概率最大，则 的可能值为（ ） A．3 B．4 C．2 和 5 D．3 和 4 7.已知 f(x)是定义在 R 上的函数，f(1)=1，且对任意 x∈R 都有 f(x＋1)≤f(x)＋1，f(x＋ 5)≥f(x)＋5，则 f(6)的值是（　） A．6　　　 B．5 C．7　　　　D．不能确定 8．称 为两个向量 、 间的“距离”.若向量 、 满足:① ;② ;③对 任意的 ,恒有 则（ ） A、 B、 C、 D、 9.直线 与圆 交于 、 两点,若满足 ,则 ( 为 坐标原点)等于( ). A. B. C. D. 10. 已知函数 的定义域为[—2， ，部分对应值如下表， 为 的导函数，函数 的图象如右图所示： 若两正数 满足 ，则 的取值范围是（ ） A． B． C． D． 二、填空题：本小题共 5 小题，每小题 5 分，共 25 分，将答案填在题中相应的横线上。 11. 若 的展开式中的 x3 项的系数为 20， 则非零实数 a = 12．在 0, 1，2，3，4，5 这六个数字所组成的没有重复数字的三位数中，其各个数字之和为 9 的 三位数共有 个（用数字做答） 13．若不等式 的解集中的整数有且仅有 1，2，3，则 b 的取值范围 _____ 14．如果直线 y＝kx＋1 与圆 交于 M、N 两点，且 M、N 关于直线 x＋y＝0 对称，则不等式组： 表示的平面区域的面积是 )3,3 1(− 0422 =−+++ mykxyx    ≥ ≤− ≥+− 0 0 01 y mykx ykx —2 0 4 1 —1 1 nC n ||),( babad −= a b a b 1|| =b ba ≠ Rt ∈ ),(),( badbtad ≥ ba ⊥ )( baa −⊥ )( bab −⊥ )()( baba −⊥+ 0Ax By C+ + = 2 2 4x y+ = M N 2 2 2C A B= + OM ON⋅  O 2− 1− 0 1 )(xf )∞+ )(' xf )(xf )(' xfy = ,a b (2 ) 1f a b+ < 3 3 b a + + )3 4,7 6( )3 7,5 3( )5 6,3 2( 26 )1()1( axx −+ 3 4x b− < x )(xf 15．已知：对于给定的 及映射 ，若集合 ，且 中所有元素对应 的象之和大于或等于 ，则称 为集合 的好子集。 ①对于 ，映射 ，那么集合 的所有好子集的个数为 ； ②对于给定的 ， ，映射 的对应关系如下表： 1 2 3 4 5 6 1 1 1 1 1 若当且仅当 中含有 和至少 中 2 个整数或者 中至少含有 中 5 个整数时， 为集合 的好 子集，写出所有满足条件的数组 ： 。 三、解答题：本大题共 6 小题，75 分，解答应写出必要的文字说明，证明过程或演算步骤。 16.(本小题满分 12 分) 已知 ,设 . (1)求函数 的最小正周期； (2)当 时,求函数 的最大值及最小值. 17．（本小题满分 12 分） 如图，在三棱锥 P-ABC 中， PA=3，AC=AB=4，PB=PC=BC=5，D、E 分别是 BC、AC 的中点， F 为 PC 上的一点，且 PF:FC=3:1． （1）求证：PA⊥BC； （2）试在 PC 上确定一点 G，使平面 ABG∥平面 DEF； （3）在满足（2）的情况下，求二面角 G-AB-C 的平面 角的正切值． 18．（本小题满分 12 分） 一个口袋中装有 2 个白球和 个红球（ 且 ），每次从袋中摸出两个球（每次摸球后把 这两个球放回袋中），若摸出的两个球颜色相同为中奖，否则为不中奖。 （1）试用含 的代数式表示一次摸球中奖的概率； （2）若 ，求三次摸球恰有一次中奖的概率； A *q N∈ : , *f A B B N→ ⊆ C A⊆ C q C A { }2, , ,q A a b c= = : 1,f x x A→ ∈ q 1,2,3,4,5,6,A π= :f A B→ x π ( )f x y z C π A C A C A ( , , )q y z )cos2,sin(cos),sin,sin(cos xxxbxxxa −=+= baxf ⋅=)( )(xf [0, ]2x π∈ )(xf n 2n ≥ n N ∗∈ n 3n = A P B C DE F （3）记三次摸球恰有一次中奖的概率为 ，当 为何值是时， 最大? 19．（本小题满分 12 分） 已知 ，其中 是自然常数， （1）讨论 时, 的单调性、极值； （2）求证：在（1）的条件下， ； （3）是否存在实数 ，使 的最小值是 3，若存在，求出 的值；若不存在，说明理由. 20．（本题满分 13 分） 在 四 边 形 中 ， 已 知 ， 点 在 轴 上 ， ， 且 对 角 线 ． （Ⅰ)求点 的轨迹方程； （Ⅱ)若点 是直线 上任意一点，过点 作点 的轨迹的两切线 、 ， 、 为切点， 为 的中点．求证： 轴； （Ⅲ）在(Ⅱ)的条件下，直线 是否恒过一定点？若是，请求出这个定点的坐标；若不是， 请说明理由． 21．（本小题满分 14 分） 设单调递增函数 的定义域为 ，且对任意的正实数 x,y 有： 且 ． ⑴、一个各项均为正数的数列 满足: 其中 为数列 的前 n 项和,求数列 的通项公式； ⑵、在⑴的条件下，是否存在正数 M 使下列不等式： 对一切 成立？若存在，求出 M 的取值范围；若不存在，请说明理由 x xxgexxaxxf ln)(],,0(,ln)( =∈−= e .a R∈ 1=a ( )f x 1( ) ( ) 2f x g x> + a ( )f x a ( )f p n ( )f p ABCD (0,0), (0,4)A D B x //BC AD AC BD⊥ C P 52 −= xy P C PE PF E F M EF PM ⊥ x EF ( )f x ( )0,+∞ ( ) ( ) ( )f xy f x f y= + 1( ) 12f = − { }na ( ) ( ) ( 1) 1n n nf s f a f a= + + − nS { }na { }na 1 2 1 22 2 1(2 1)(2 1) (2 1)n n na a a M n a a a⋅ ≥ + − − −  *n N∈ 高考数学交流题参考答案 题号 1 2 3 4 5 6 7 8 9 10 答案 D D A B D A A C A B 11． 5 12. 16 13. 14. 5 < b < 7 15. 4 (5,1,3) 16.(本小题满分 12 分) (1) = = …………2 分 = = = = ∴ 的最小正周期 ． …………6 分 (2) ∵ , ∴ . …………8 分 ∴当 ,即 = 时, 有最大值 ; …………10 分 当 ,即 = 时, 有最小值-1． …………12 分 17.(本小题满分 12 分) 解：(1) 在△PAC 中，∵PA=3，AC=4，PC=5， ∴ ，∴ ；……1 分 又 AB=4，PB=5，∴在△PAB 中， 同理可得 …………………………2 分 ∵ ，∴ …… ∵ 平面 ABC，∴PA⊥BC. …………3 分 (2) 如图所示取 PC 的中点 G，…………………4 分 4 1  baxf ⋅=)( xxxxxx cos2sin)sin(cos)sin(cos ⋅+−⋅+ xxxx cossin2sincos 22 +− xx 2sin2cos + )2sin2 22cos2 2(2 xx + 2(sin cos2 cos sin2 )4 4x x π π+ )42sin(2 π+x )(xf π=T 0 x≤ ≤ 2 π 524 4 4x π π π≤ + ≤ 242 ππ =+x x 8 π )(xf 2 52 4 4x π π+ = x 2 π )(xf 222 PCACPA =+ ACPA ⊥ ABPA ⊥ AABAC = ABCPA 平面⊥ ⊂BC 连结 AG，BG，∵PF:FC=3:1,∴F 为 GC 的中点 又 D、E 分别为 BC、AC 的中点， ∴AG∥EF，BG∥FD，又 AG∩GB=G，EF∩FD=F，……………6 分 ∴面 ABG∥面 DEF． 即 PC 上的中点 G 为所求的点． …………… 7 分 (3)由(2)知 G 这 PC 的中点，连结 GE，∴GE⊥平面 ABC，过 E 作 EH⊥AB 于 H，连结 GH，则 GH⊥AB，∴∠EHG 为二面角 G-AB-C 的平面角． …………… 9 分 ∵ 又 ∴ 又 …………… 11 分 ∴ ∴二面角 G-AB-C 的平面角的正切值为 ． …………… 12 分 18.(本小题满分 12 分) 解：（1）∵一次摸球从 个球中任选两个，有 种选法， 任何一个球被选出都是等可能的，其中两球颜色相同有 种选法， ∴一次摸球中奖的概率 ． （2）若 ，则一次摸球中奖的概率 ， 三次摸球是独立重复试验，三次摸球恰有一次中奖的概率是 ． （3）设一次摸球中奖的概率为 ，则三次摸球恰有一次中奖的概率为 ， ， ∵ ， ∴ 在 上为增函数，在 上为减函数． ∴当 时， 取得最大值． ∵ ≥ ， 解得 ． 8 395 2 1 == ∆∆ ABCABE SS EHABS ABE ⋅=∆ 2 1 16 395 4 4 395 2 === ∆ AB SEH ABE 2 3 2 1 == PAGE 65 398 395 16 2 3tan =×==∠ EH EGEHG 65 398 2n + 2 2Cn+ 2 2 2C Cn + 2 2 2 2 2 2 2 C C 2 C 3 2 n n n np n n+ + − += = + + 3n = 2 5p = 1 2 3 3 54(1) C (1 ) 125P p p= ⋅ ⋅ − = p ( ) ( )21 3 2 3 3(1) C 1 3 6 3f p P p p p p p= = ⋅ ⋅ − = − + 0 1p< < ( ) ( )( )29 12 3 3 1 3 1f p p p p p′ = − + = − − ( )f p 10 3     ， 1 13     ， 1 3p = ( )f p 2 2 2 1 3 2 3 n np n n − += =+ + (n )*2, n∈N且 2n = 故当 时，三次摸球恰有一次中奖的概率最大． 19.(本小题满分 12 分) （1） ， ∴当 时， ，此时 单调递减 当 时， ，此时 单调递增 ∴ 的极小值为 （2） 的极小值为 1，即 在 上的最小值为 1， ∴ ， 令 ， ， ……6 分 当 时， ， 在 上单调递增 ……7 分 ∴ ∴在（1）的条件下， （3）假设存在实数 ，使 （ ）有最小值 3， ①当 时， 在 上单调递减， ， （舍去），所以， 此时 无最小值. ……10 分 ②当 时， 在 上单调递减，在 上单调递增 ， ，满足条件. ③ 当 时， 在 上单调递减， ， （舍去），所 以，此时 无最小值.综上，存在实数 ，使得当 时 有最小值 3. 20.(本小题满分 13 分) （Ⅰ)如图，设点 的坐标为 ， 则 ，  xxxf ln)( −= x x xxf 111)( −=−=′ 10 << x / ( ) 0f x < ( )f x ex <<1 / ( ) 0f x > ( )f x ( )f x 1)1( =f  ( )f x ( )f x ],0( e 0)( >xf min( ) 1f x = 2 1ln 2 1)()( +=+= x xxgxh x xxh ln1)( −=′ ex <<0 0)( >′ xh ( )h x ],0( e minmax |)(|12 1 2 1 2 11)()( xfeehxh ==+<+== 1( ) ( ) 2f x g x> + a xaxxf ln)( −= ],0( ex ∈ / 1( )f x a x = − x ax 1−= 0≤a )(xf ],0( e 31)()( min =−== aeefxf ea 4= )(xf ea << 10 )(xf )1,0( a ],1( ea 3ln1)1()( min =+== aafxf 2ea = ea ≥1 )(xf ],0( e 31)()( min =−== aeefxf ea 4= )(xf 2ea = ],0( ex ∈ ( )f x 2n = C ),( yx )0,0( ≠≠ yx ( ,0), ( , ), ( ,4)B x AC x y BD x= = −  ， ，即 ． ∴所求的轨迹 是除去顶点的抛物线 ……………… 3 分 （解法一）(Ⅱ)对函数 求导得， ． 设切点坐标为 ，则过该切点的切线的斜率是 ，该切线方程是 ． 又设点 的坐标为 ， 切线过点 ， 有 ， 化简，得 ． …………………………6 分 设 、 两点的坐标分别为 、 ，则 、 为方程 的两根， ． 因此，当 时，直线 与 轴重合，当 时，直线 与 轴平行 …………9 分 (Ⅲ) ． 点 的坐标为 ． 又 ． 直线 的方程为： ，即 ．………（ ） 当 时，方程（ ）恒成立， 对任意实数 ，直线 恒过定点，定点坐标为 ． …………………………14 分 （ 解 法 二 ） ( Ⅱ ) 设 点 的 坐 标 为 ， 利 用 切 点 弦 直 线 方 程 的 结 论 可 得 出 直 线 的 方 程 为 ，即 …………………………7 分 由 得 . ． . 因此，当 时，直线 与 轴重合，当 时，直线 与 轴平行. ……………9 分 (Ⅲ) 由(Ⅱ)得知直线 的方程为 ，即 ． 后面解法同解法一. AC BD⊥   ( ) 4 0x x y∴ ⋅ − + ⋅ = 21 4y x x= ≠ ( 0) T 21 4y x= 1 2y x′ = 2 0 0 1( , )4x x 0 1 2 x 2 0 0 0 1 1 ( )4 2y x x x x− = − P )52,( −tt  P ∴ )(2 1 4 152 00 2 0 xtxxt −=−− 02082 0 2 0 =−+− ttxx A B 2 1 1 1( , )4x x 2 2 2 1( , )4x x 1x 2x 020822 =−+− ttxx 208,2 2121 −==+ txxtxx 1 2 2M x xx t +∴ = = 0=t PM y 0≠t PM y  2 2 1 2 1 1 1( )2 4 4My x x= + 522 1)]208(24[8 1]2)[(8 1 22 21 2 21 +−=−−=−+= ttttxxxx ∴ M )522 1,( 2 +− ttt 2 21 1 1 24 4 1 2 1 2 1 1 1( ) 24 4 2AB x xk x x t tx x −= = + = ⋅ =− ∴ AB )(2 1)522 1( 2 txttty −=+−− 0210)4( =−+− yxt ∗  5,4 == yx ∗ ∴ t AB )5,4( P )52,( −tt AB txty 4 1 2 )52( =−+ 522 1 +−= ttxy    = +−= .4 1 ,52 2 2 1 xy ttxy 020822 =−+− ttxx 208,2 2121 −==+∴ txxtxx 1 2 2M x xx t +∴ = = 0=t PM y 0≠t PM y AB 522 1 +−= ttxy 0210)4( =−+− yxt 21.(本小题满分 13 分) ⑴、 对任意的正数 均有 且 ．………2 分 又 ，　　………………………………………………………4 分 又 是定义在 上的单增函数， ． 当 时， ， ． ， ． 当 时， ， ． ， 为 等 差 数 列 ， ， ． …………………………………………………………………6 分 ⑵、假设 存在满足条件， 即 对一切 恒成立．　……………８分 令 ， ，　……………………………10 分 故 ，…………………………………12 分 ， 单调递增， ， ． ．　　……………………………………………………………………14 分  x y、 ( ) ( ) ( )f xy f x f y= + 1( ) 12f = −  10 ( ) ( ) ( 1) 1 ( ) ( 1) ( )2n n n n n na f S f a f a f a f a f> = + + − = + + +且 ∴ 2 1( ) [( ) ]2n n nf S f a a= + × ( )f x ( ]0,+∞ ∴ 21 ( )2n n nS a a= + 1n = 2 1 1 1 1 ( )2a a a= + 2 1 1 0a a∴ − = 1 0a > 1 1a∴ = 2n ≥ 2 2 1 1 12 2 2n n n n n n na S S a a a a− − −= − = + − − 1 1( )( 1) 0n n n na a a a− −∴ + − − = 10 1( 2)n n na a a n−> ∴ − = ≥ { }na∴ 1 1, 1a d= = na n∴ = M 1 2 1 2 2 2 1(2 1)(2 1) (2 1) n n n a a aM n a a a ≤ + − − −   *n N∈ 1 2 1 2 2( ) 2 1(2 1)(2 1) (2 1) n n n a a ag n n a a a = + − − −   ∴ 12 1 2 ( 1)( 1) 2 3 1 3 (2 1)(2 1) n n ng n n n n + × × × × × ++ = + × × × × − +   2 2 ( 1) 2 2 4 8 4 1( ) 4 8 32 1 2 3 g n n n n g n n nn n + + + += = >+ ++ + ( 1) ( )g n g n∴ + > ∴ ( )g n *n N∴ ∈ ( ) (1)g n g≥ = 2 3 3 ∴ 2 30 3M< ≤ 湖北省黄冈中学高考数学模拟考试 4 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分，在每小题给出的四个选项中，只有一项是 满足题目要求的。 1. 不等式 10 成立的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．非充分非必要条件 2.已知 ， ，且 ∥ ，则 为（ ） A、 B、 C、 或 D、 或 3. 设集合 ， ， , 若 ，则 b = c 的概率是 A B C D 4. .向量 =( )， 是直线 y=x 的方向向量，a =5,则数列 的前 10 项的和 A 50 B 100 C 150 D 200 5. , 则 被3除的余数是 A.0 B.1 C.2 D.不能确定 6. 已知 x，y 满足条件Error!则 z＝ x＋y＋2 x＋3 的最小值（ ） A 4 B C D - 7. 函数 图象如图，则函数 的单调递减区间为 （A） （B） （C） （D） 8．若动直线 与函数 的图象分别交于 M、N 两点， 则|MN|的最大值为 A． B 1 C 2 D 3 9. 直线 MN 与双曲线 C: 的左右支分别交与 M、N 点，与双曲线 C 的右准线相交于 P 点， F 为右焦点，若 ,又 ( ),,则实数 的值为 A B 1 C 2 D 2 π ( )1,2= → a 52= → b → a → b b → ( )2,4− ( )2,4 ( )2,4 − ( )2,4− ( )2,4 −− ( )2,4 }1,{bP = }2,1,{cQ = QP ⊆ }9,8,7,6,5,4,3,2{, ∈cb 8 1 4 1 2 1 4 3 V n nn n a aaa 2,2 2 1 1 + + − V 1 { }na 2010 2010 2 210 2010)42( xaxaxaax ++++=+  2010420 aaaa ++++  6 13 3 1 3 2 3 2( )f x x bx cx d= + + + )33 2(log 2 2 cbxxy ++= ),2 1[ +∞ ),3[ +∞ ]3,2[− ]2,( −−∞ ax = )12cos()()12sin(3)( ππ +=+= xxgxxf 与 3 12 2 2 2 =− b y a x FNFM 2= PMNP λ= R∈λ λ 2 1 3 1 －2 3 y x 0 10. 已知两个不相等的实数 满足以下关系式： ，则连接 A 、 B 两点的直 线与圆心在原点的单位圆的位置关系是 ． A 相离 B 相交 C 相切 D 不能确定 二、填空题：本大题共 5 小题，每题 5 分，共 25 分.请将答案填在答题卡对应题号的位置上。 11. 如果函数 f(x)= 则不等式 xf(x) 的解集为_______________. 12. 设递增等差数列 的公差为 d,若 a ,a ,a ,a ,a ,a ,a 的方差为 1，则 d=________. 13. 将A、B、C、D、E五种不同的文件放入一排编号依次为1、2、3、4、5、6的六个抽屉内，每个 抽屉至多放一种文件.若文件A、B必须放入相邻的抽屉内，文件C、D也必须放相邻的抽屉内，则文 件放入抽屉内的满足条件的所有不同的方法有 96 种． 14. 已知点 M 是抛物线 y =4x 的一点，F 为抛物线的焦点，A 在圆 C:(x-4) +(y-1) =1 上，则 的最小值为__________ 15. ． 如 图 , 在 三 棱 锥 中 , 、 、 两 两 垂 直 , 且 . 设 是 底 面 内 一 点 , 定 义 , 其中 、 、 分别是三棱锥 、 三棱锥 、 三 棱 锥 的 体 积 . 若 , 且 恒成立,则正实数 的最小值为________. 1 16.已知锐角 的三内角 A、B、C 的对边分别是 （1）求角 A 的大小； （2）求 的值。 P ABC− PA PB PC 3, 2, 1PA PB PC= = = M ABC ( ) ( , , )f M m n p= m n p M PAB− M PBC− M PCA− 1( ) ( , , )2f M x y= 1 8a x y + ≥ a a b、 2 04a sin a cos πθ θ⋅ + ⋅ − = ， 2 04b sin b cos πθ θ⋅ + ⋅ − = ( )2a ,a ( )2b ,b    >− ≤ 11 11 x x 0≥ { }na 1 2 3 4 5 6 7 2 2 2 MFMA + ABC∆ .3tan)(,,, 222 bcAacbcba =−+且 )]10tan(31[)10sin( °−−⋅°+ AA 第 15 题 M C B A P 17.．某地区试行高考考试改革：在高三学年中举行 5 次统一测试，学生如果通过其中 2 次测试即可 获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加 5 次测试. 假 设某学生每次通过测试的概率都是 ，每次测试通过与否互相独立. 规定：若前 4 次都没有通过测 试，则第 5 次不能参加测试. (Ⅰ) 求该学生考上大学的概率. (Ⅱ) 如果考上大学或参加完 5 次测试就结束，记该生参加测试的次数为ξ，求 P( ) 18.如图，在 中， ，斜边 ． 可以通过 以直线 为轴旋转得到，且二面角 是直二面角．动点 的斜边 上． （1）求证：平面 平面 ； （2）当 为 的中点时，求异面直线 与 所成角的大小； （3）求 与平面 所成角的最大值． 19. 如图，已知直线 的右焦点 F，且交椭圆 C 于 A，B 两点，点 A，F，B 在直线 上的射影依次为点 D，K，E，若抛物线 的焦点为椭圆 C 的上顶点。 (1)求椭圆 C 的方程； (2)若直线 L 交 y 轴于点 M，且 ，当 m 变 化时，求 的值； Rt AOB△ π 6OAB∠ = 4AB = Rt AOC△ Rt AOB△ AO B AO C− − D AB COD ⊥ AOB D AB AO CD CD AOB 1 3 3>ξ )0(1:1: 2 2 2 2 >>=++= bab y a xCmyxL 过椭圆 2: axG = yx 342 = BFMBAFMA 21 , λλ == 21 λλ + O C A D B 20.已知函数 f(x)=ax +bx +cx 在 x=x 处取得极小值-4，使其导数 f (x)>0 的 x 的取值范围 （1，3）。 （1）求 f(x)的解析式； （2）若过点 A（-1，m）可作曲线 y=f(x)的三条切线，求实数 m 的取值范围。 21.已知数列 满足 , ,若 b = a -a （I）证明：数列 为等比数列，并求数列 的通项公式. （II）求使不等式 成立的所有正整数 m，n 的值. 参考答案 1-10 ADＣAC CDCAB 11． 12． 13．96 14．4 15．1 解：（1）由已知条件及余弦定理得 ∴ . ∵ ……………………6 分 （2） = sin70 3 2 0 ' { }na 1 2a 2,a 3= = n+1 n n 12a 3a a −= − ( )*n N n 2∈ ≥且 1+n 1+n n { }nb { }na n n 1 a m 2 a m 3+ − <− { }1x0,1 ≤≤−< 或xx 2 1 3 sin 3tan , ,2 cos cos 2cos bc AA bc A A A = ∴ = 3sin 2A = (0, )2A π∈ , .3A π=故 )50cos 50sin31(70sin)]10tan(31)[10sin( ° °−°=°−−°+ AA    50cos 50sin350cos − =2sin70 = =－ =－1 ……….12 17. 解 ： （ Ⅰ ） 记 “ 该 生 考 上 大 学 ” 的 事 件 为 事 件 A ， 其 对 立 事 件 为 ， 则 ∴ ……6 分 （Ⅱ）该生参加测试次数ξ的可能取值为 2，3，4，5. ， ∴ P( )=P( =4)+P( =5) = ………………12 18.解：（I）由题意， ， ， 是二面角 的平面角， 又 二面角 是直二面角， ，又 ， 平面 ， 又 平面 ． 平面 平面 ．--------------------------------------------------------4 分 （II）作 ，垂足为 ，连结 ，则 ， 是异面直线 与 所成的角． - -------------------------5 分 在 中， ， ， ． 又 ． 在 中， ． - --------------------7 分 异面直线 与 所成角的大小为 ．- ----------------------8 分 （III）由（I）知， 平面 ， 是 与平面 所成的角，且 ． 当 最小时， 最大 ------------------10 分 CO AO⊥ BO AO⊥ BOC∴∠ B AO C− −  B AO C− − CO BO∴ ⊥ AO BO O=  CO∴ ⊥ AOB CO ⊂ COD ∴ COD ⊥ AOB DE OB⊥ E CE DE AO∥ CDE∴∠ AO CD Rt COE△ 2CO BO= = 1 12OE BO= = 2 2 5CE CO OE∴ = + = 1 32DE AO= = ∴ Rt CDE△ 5 15tan 33 CECDE DE = = = ∴ AO CD 15arctan 3 CO ⊥ AOB CDO∴∠ CD AOB 2tan OCCDO OD OD = = OD CDO∠    50cos )5030sin( −   40sin 20cos20sin2 A .243 112 81 16 243 64)3 2()3 2()3 2)(3 1()( 431 4 =+=+= CAP 112 131( ) 1 ( ) 1 .243 243P A P A= − = − = 2 1 4 3 1 2 1 2 4 16 28( 4) ( )3 3 3 3 27 81 81P Cξ      = = ⋅ ⋅ ⋅ + = + = 3 1 4 1 2 32( 5) .3 3 81P Cξ            = = ⋅ ⋅ = 3>ξ ξ ξ 27 20 这时， ，垂足为 ， ， ， 与平面 所成角的最大值为 ．- ----------------------12 19. 解：（1）易知 …………………4 分 （2）设 …………………………8分 又由 同理 …………………………………12分 20.解：（1）f (x)=3ax +2bx+c,依题意有 a>0, 1,3 分别为 f(x)的极值小，极大值点…2 分 解得 a=-1 b=6 c=-9 ……………………6 分 （2）设过 P 点的切线切曲线（x ,y ）,则切线的斜率 k=-3 x +12 x -9 切线方程为 y=（-3 x +12 x -9）(x+1)+m, OD AB⊥ D 3=⋅= AB OBOAOD 3 32tan =∠CDO CD∴ AOB 2 3arctan 3 ∴ )0,1(,33 2 Fbb 又=∴= 41 222 =+==∴ cbac 134 22 =+∴ yxC的方程为椭圆 )1,0( mMyl −轴交于与    =−+ += 01243 1),(),,( 222211 yx myxyxByxA 由 0)1(144096)43( 222 >+=∆=−++∴ mmyym (*)3 211 21 m yy =+∴ ),1()1,( 111111 yxmyxAFMA −−=+∴= λλ 1 1 11 my −−=∴λ 2 2 11 my −−=λ 3 8 3 22)11(12 21 21 −=−−=+−−=+∴ yym λλ 3 8 21 −=+∴ λλ ' 2 4)1( 0)3( 0)1( ' ' = = =    f f f 0 0 0 2 0 0 2 0 故 y =（-3 x +12 x -9）（x +1）+m=- x +6 x -9 x ……………..8 分 要使过 P 可作曲线 y=f(x)三条切线，则方程关于（-3 x +12 x -9）（x +1）+m=- x +6 x -9 x 有三解。m=2 x -3 x -12 x +9,令 g(x)= 2 x -3 x -12 x+9， g (x)=6x -6x-12=6(x+1)(x-2)=0,易知 x=-1,2 为 g(x)的极值大、极小值点 …10 分 故 g(x) =-11,g(x) =16, 故满足条件的 m 的取值范围-11a …………8 分 ∴a >m>a ( n 2), 即 当 n=2，解得 2 + − 1 1 n n am am 3≥    << ≥> + − 4 3 1 1 n n am am n n 1 a m 2 a m 3+ − <− ma ma − − 2 1 湖北省黄冈中学高考数学模拟考试 5 一、选择题（本大题共 10 小题，每小题 5 分，共 50 分．在每小题给出的四个选项中，只有一项是 符合题目要求的） 1．已知 为两不相等的实数，集合 ，映射 表示把 中的元素 映射到集合 中仍为 ，则 等于（ ） A．1 B．2 C．3 D．4 2．已知 为平面，命题 p：若 ，则 ；命题 q：若 上不共线的三点到 的距离相等，则 ．对以上两个命题，下列结论中正确的是（ ） A．命题“p 且 q”为真 B．命题“p 或 ”为假 C．命题“p 或 q”为假 D．命题“ ”且“ ”为假 3．设随机变量 服从标准正态分布 ，已知 ，则 = （ ） A．0.025 B．0.050 C．0.950 D．0.975 4． 若不等式 的解集为 ，则实数 的值为（ ）. A． B． C．36 D． 5．已知函数 为偶函数 ，其图像与直线 y=2 某两个交点的横坐标分别为 x1、 x2，若|x2-x1|的最小值为 ，则该函数在区间（ ）上是增函数。 A． B． C． D． 6．函数 与 轴交点的个数是 （ ） A、0 B、1 C、2 D、3 7．如果关于 x 的一元二次方程 中，a、b 分别是两次投掷骰子所得的点 数，则该二次方程有两个正根的概率 P= （ ） A． B． C． D． 8．已知 是等比数列， ，则 的取值范围是（ ） , ,α β γ ,βα ⊥ β γ⊥ //α γ α β βα // q¬ p¬ q¬ ξ ( 0 1)N ， ( 1.96) 0.025Φ − = (| | 1.96)P ξ < ,a b 2 2{ 4 , 1}, { 4 1, 2}M a a N b b= − − = − + − :f M N→ M x N x a b+ 3 2x ax> + ( )4,b b 9 18 48 2sin( )y xω θ= + (0 )θ π< < π ,2 4 π π − −   ,4 4 π π −   0, 2 π     3,4 4 π π     ( ) 2 3 1 2 3 x xf x x= + + + x 09)3(2 22 =+−−− bxax 18 1 9 1 6 1 18 13 { }na 4 1,2 52 == aa ( )∗ + ∈+⋅⋅⋅++ Nnaaaaaa nn 13221 A. B. C. D. 9．已知 、 为非零的不共线的向量，设条件 ；条件 对一切 ，不等式 恒成立．则 是 的（　　） Ａ．必要而不充分条件　　　　　　　Ｂ．充分而不必要条件 Ｃ．充分而且必要条件　　　　　　　Ｄ．既不充分又不必要条件 10.　已知双曲线 的离心率为 e，左、右两焦点分别为 F1、F2，焦距为 ，抛物线 C 以 F2 为顶点，F1 为焦点,点 P 为抛物线与双曲线右支上的一个交点，若 a|PF2|＋c|PF1| ＝8a2，则 e 的值为 ( ) A. 3 B. 3 C. 2 D. 6 二、填空题：本大题共 5 小题，每小题 5 分，共 25 分. 把答案填在答题卡的相应位置上. 11 ． 若 ， 且 ， 则 实 数 的 值 为 __________． 12．在 的边 上有 、 、 、 四点， 边上有 、 、 、 , 五点，共 9 个点，连结线段 ，如果其中两条线段不相交，则称之为一对“和睦线”，则共有 _______________对. 13．如图，O 是半径为 1 的球心，点 A、B、C 在球面上， OA、OB、OC 两两垂直，E、F 分别为大圆弧 AB 与 AC 的中点，则点 E、F 在该球上的球面距离是______ 14．已知 的最大值为 15．直线 和圆 交于点 A、B，以 轴的正方向为始边，OA 为终边（O 是坐标原 点）的角为 ，OB 为终边的角为 ，那么 是 . 三、解答题：本大题共 6 小题，共 75 分. 解答应写出文字说明、证明过程或演算步骤. 16． (本小题满分 12 分)已知向量 ，定义函数 [ )16,12 [ )16,8      3 32,8      3 32,3 16 a b :M ( )bab −⊥ :N Rx ∈ babxa −≥− M N 2 2 2 2: 1( 0, 0)x yE a ba b − = > > 2c 6 6 2 210 6)1( xaxaxaamx +⋅⋅⋅+++=+ 1 2 6 63a a a+ +⋅⋅⋅+ = m AOB∠ OA 1A 2A 3A 4A OB 1B 2B 3B 4B 5B (1 4,1 5)i j≤ ≤ ≤ ≤ yxyxz yx yx 42, 3 1)2()2( 22 22 +++=    ≤+ ≤−+− 则 2y x m= + 2 2 1x y+ = x α β sin( )α β+ ( ) ( )2sin ,cos , 3 cos ,2cosm x x n x x= =  ，求函数 的最小正周期、单调递增区间. 17．（本题满分 12 分） 某地区试行高考考试改革：在高三学年中举行 5 次统一测试，学生如果通过其中 2 次测试即可 获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加 5 次测试. 假 设某学生每次通过测试的概率都是 ，每次测试通过与否互相独立. 规定：若前 4 次都没有通过测 试，则第 5 次不能参加测试. (Ⅰ) 求该学生考上大学的概率. (Ⅱ) 如果考上大学或参加完 5 次测试就结束，记该生参加测试的次数为ξ，求ξ的分布列及ξ的 数学期望. 18（本小题满分 12 分）如图，在四棱锥 P-ABCD 中，底面 ABCD 为直角梯形，且 AB//CD，AB⊥AD， AD=CD=2AB=2．侧面 为正三角形，且平面 PAD⊥平面 ABCD． （1） 若 M 为 PC 上一动点，则 M 在何位置时，PC⊥平面 MDB？ 并加已证明． （Ⅱ）若 G 为 的重心，求二面角 G—BD—C 大小 19．（本小题满分 12 分）设函数 。 （Ⅰ）若在定义域内存在 ，而使得不等式 能成立，求实数 的最小值； （Ⅱ）若函数 在区间 上恰有两个不同的零点，求实数 的取值范围。 20．（本题满分 13 分） 已知椭圆 ，直线 与椭圆交于 、 两点， 是线段 的中点，连接 并延长交椭圆于点 。 （Ⅰ）设直线 与直线 的斜率分别为 、 ，且 ，求椭圆的离心率的取值范 围。 （Ⅱ）若直线 经过椭圆的右焦点 ，且四边形 是面积为 的平行四边形，求直线 倾 斜 角 的大小。 2( ) (1 ) 2ln(1 )f x x x= + − + 0x 0( ) 0f x m− ≤ m 2( ) ( )g x f x x x a= − − − [ ]0,2 a ( ) ( )( )log 1 0, 1af x m n a a= − > ≠   ( )f x 1 3 PAD∆ PBC∆ 2 2 2 2 1( 0)x y a ba b + = > > l A B M AB OM C AB OM 1k 2k 1 2 1 2k k⋅ ≥ − AB ( ,0)F c OACB 3 5 10 ac AB A B C D P （21）（本小题共 14 分） 如果正数数列 满足：对任意的正数 M，都存在正整数 ，使得 ，则称数列 是 一个无界正数列． （Ⅰ）若 ， 分别判断数列 、 是否为无界正数列，并说明理由； （Ⅱ）若 ，是否存在正整数 ，使得对于一切 ，有 成立； （Ⅲ）若数列 是单调递增的无界正数列，求证：存在正整数 ，使得 ． 参考答案及评分标准 1-5 DCCCA 6-10 BACCA 11.1 或-3 12。 60 13。 14。15 15。 16．解：因为 所以 故 …………6 分 令 ，则 的单调递增的正值区间是 ，单调递减的正值区间是 { }na 0n 0na M> { }na ( )3 2sin( ) 1,2,3,na n n= + =  1 , 1,3,5, , 1, 2,4,6, ,2 n nnb n n  ==  + =   { }na { }nb 2na n= + k n k≥ 1 2 2 3 1 1 2 n n aa a na a a + + + + < − { }na m 1 2 2 3 1 2009m m m aa a a a a + −+ + + < 3 π 4 5 − 22 3sin cos 2cos 3sin 2 cos2 1m n x x x x x= + = + +   ( ) ( )log 3 sin 2 cos 2 log 2sin 2 6a af x x x x   = + = +     π 2 2T = =π π ( ) 2sin 2 6g x x = +   π ( )g x ( ),12 6k k k Z − + ∈   π ππ π ( )5,6 12k k k Z π ππ π + + ∈  当 时，函数 的单调递增区间为 当 时，函数 的单调递增区间为 （注：区间为开的不扣 分）…………12 分 17 ． 解 ： （ Ⅰ ） 记 “ 该 生 考 上 大 学 ” 的 事 件 为 事 件 A ， 其 对 立 事 件 为 ， 则 ∴ ……6 分 （Ⅱ）该生参加测试次数ξ的可能取值为 2，3，4，5. ， ， ， 故ξ的分布列为： ……12 分 18．解：（1）当 M 为 PC 的中点时，PC⊥平面 MDB．------------------1 分 事实上，连 BM，DM，取 AD 的中点 N，连 NB，NP． 因为 ，且平面 PAD 平面 ABCD，所以 PN⊥平面 ABCD． 在 中， ，所以 ，又 所以 ，又 ， 平面 MDB， 而 PD=DC=2，所以 ，所以 平面 MDB------------------6 分 （2）易知 G 在中线 BM 上，过 M 作 于 F，连 CF， 因为 平面 MDB，所以 ， 故 是二面角 G—BD—C 的平面角 ------------------9 分 在 中， ，所以 ，又 所以 ，故二面角 G—BD—C 的大小为 ----------------12 分 19．解：(Ⅰ)要使得不等式 能成立，只需 。 求 导 得 ： ， ∵ 函 数 得 定 义 域 为 0( ) 0f x m− ≤ min( )m f x≥ 1 2 ( 2)( ) 2(1 ) 21 1 x xf x x x x +′ = + − =+ + ( )f x 0 1a< < ( )f x ( )5,6 12k k k Z + + ∈  π ππ π 1a > ( )f x ( ),12 6k k k Z − + ∈   π ππ π A .243 112 81 16 243 64)3 2()3 2()3 2)(3 1()( 431 4 =+=+= CAP 112 131( ) 1 ( ) 1 .243 243P A P A= − = − = 21 1( 2) 3 9P ξ      = = = 1 2 1 2 1 4( 3) . . .3 3 3 27P Cξ = = = 2 1 4 3 1 2 1 2 4 16 28( 4) ( )3 3 3 3 27 81 81P Cξ      = = ⋅ ⋅ ⋅ + = + = 3 1 4 1 2 32( 5) .3 3 81P Cξ            = = ⋅ ⋅ = .81 326 81 32581 28427 439 12 =×+×+×+×=ξE PN AD⊥ ⊥ Rt PNB∆ 3, 2PN NB= = 5PB = 5BC = BN PC⊥ MD BM M= ,MD BM ⊂ DM PC⊥ PC ⊥ MF BD⊥ PC ⊥ CF BD⊥ MFC∠ Rt BDC∆ 5, 2, 5BD DC BC= = = 4 5 5CF = 2CM = 10sin 4MFC∠ = 10arcsin 4 ，当 时， ，∴函数 在区间 上是减函数； 当 时， ，∴函数 在区间(0，+∞)上是增函数。 ∴ ， ∴ 。故实数 的最小值为 。 ………6 分 (Ⅱ)由 得： 原题设即方程 在区间 上恰有两个相异实根。 设 。∵ ，列表如下： － 0 ＋ 减函数 增函数 ∵ ，∴ 。 从而有 ， 画出函数 在区间 上的草图（见右下） 易知要使方程 在区间 上恰有 两 个 相 异实根， 只需： ， 即： 。 ………12 分 20．（1）解法一：设 ， , ,则 两式相减，得： 又 ， ， ， 可得 ( 1, )− +∞ ( 1,0)x∈ − ( ) 0f x′ < ( )f x ( 1,0)− (0, )x∈ +∞ ( ) 0f x′ > ( )f x min( ) (0) 1f x f= = 1m ≥ m 1 2( ) (1 ) 2ln(1 )f x x x= + − + 2 2( ) (1 ) 2ln(1 ) ( ) 1 2ln( 1)g x x x x x a x x a= + − + − + + = + − + − (1 ) 2ln(1 )x x a+ − + = [ ]0,2 ( ) (1 ) 2ln(1 )h x x x= + − + ( ) 2 11 1 1 xh x x x −′ = − =+ + x 0 ( )0,1 1 ( )1,2 2 ( )h x′ ( )h x 1 2 2ln 2− 3 2ln3− ( ) ( )0 2 1 (3 2ln3) 2(ln3 1) 2(ln 1) 0h h e− = − − = − > − = ( ) ( )0 2h h> ( )max 1h x = ( )min 2 2ln 2h x = − ( )h x [ ]0,2 ( )h x a= [ ]0,2 2 2ln 2 3 2ln3a− < ≤ − ( ]2 2ln 2,3 2ln3a∈ − − ( )1 1,A x y ( )2 2,B x y ( )0 0,C x y 2 2 1 1 2 2 2 2 2 2 2 2 1 1 x y a b x y a b  + =  + = ( )( ) ( )( )1 2 1 2 1 2 1 2 2 2 0x x x x y y y y a b + − + −+ = 1 2 0 2 x xx += 1 2 0 2 y yy += 1 2 1 1 2 y yk x x −= − 0 2 0 yk x = ( )2 2 2 2 2 2 1 2 1 2 22 bk k a b a ca ⋅ = − ≥ − ⇒ ≥ = − 则 ， …………………………………………（5 分） 解法二：设 ， , ,，直线 ① ， ，又 由条件： 则 ， ……………………………………（5 分） （1） 设直线 AB 的倾斜角为 α 由①及 ，可知 代入椭圆方程，得 ②…………………………………………………………………（7 分） 又 ③………………………………………………………………（9 分） 由②代入③，得 = 原点 O 到直线 AB 的距离 得 或 ……………………（13 分） （21）（本小题共 12 分） 2 2 2 1 2 ce a = ≥ 20 1 12e e< < ⇒ ≤ < ( )1 1,A x y ( )2 2,B x y ( )0 0,C x y : ( 0)l x my n m= + ≠ ( )2 2 2 2 2 4 2 2 2 2 2 2 2 0x my n m b a y b mny b b x a y a b = + ⇒ + + − = + = ⇒ 1 2 0 2 y yy += 2 2 2 2 b mn m b a = − + 2 0 0 2 2 2 a nx my n m b a = + = + 2 2 2 bk ma ⇒ = − 1 1k m = 2 1 2 2 bk k a ⇒ = − ( )2 2 2 2 2 1 2 2 1 2 22 bk k a b a ca = − ≥ − ⇒ ≥ = − 2 2 2 1 2 ce a = ≥ 0 1e< < 2 12 e⇒ ≤ < n c= 2 2 2 2 2 2 2 2 2 2,a c b mcC m b a m b a  − + +  2 2 2 24c m b a= + ( )2 2 2 1 2 1 2 a a aAB AF FC e x e x e x xc c c      = + = − + − = − +           2 2 2 22 (1 )ca m b a = − + AB 3 2 a 21 cd m = + 2 3 3 5 102 1OACB ac acS AB d m ⇒ = ⋅ = = + 2m = ± 1tan 2ABk α⇒ = = ± 1arctan 2 α⇒ = 1arctan 2 π − 解：（Ⅰ） 不是无界正数列．理由如下： 取 M = 5，显然 ，不存在正整数 满足 ； 是无界正数列．理由如下： 对任意的正数 M，取 为大于 2M 的一个偶数，有 ，所以 是无界正数列． ………………………………………4 分 （Ⅱ）存在满足题意的正整数 .理由如下： 当 时， 因为 ， 即取 ，对于一切 ，有 成立. …………7 分 注：k 为大于或等于 3 的整数即可. （Ⅲ）证明：因为数列 是单调递增的正数列， 所以 . 即 . 因为 是无界正数列，取 ，由定义知存在正整数 ，使 . 所以 . 由定义可知 是无穷数列，考察数列 ， ， ，…，显然这仍是一个单调递 增 的 无 界 正 数 列 ， 同 上 理 由 可 知 存 在 正 整 数 ， 使 得 . 重复上述操作，直到确定相应的正整数 . { }na 3 2sin( ) 5na n= + ≤ 0n 0 5na > { }nb 0n 0 0 1 2 1 2 2n n Mb M + += > > { }nb k 3n ³ 1 2 2 3 1 n n aa an a a a +  − + + +    3 2 12 1 2 3 1 n n n a a a aa a a a a + + − −−= + + + 1 1 1 1 1 1 1 4 5 3 4 5 6 2n = + + + ≥ + + >+ 3k = n k≥ 1 2 2 3 1 1 2 n n aa a na a a + + + + < − { }na 1 2 2 3 1 n n aa an a a a +  − + + +    3 2 12 1 2 3 1 n n n a a a aa a a a a + + − −−= + + + 3 2 1 1 12 1 1 1 1 1 1 1 1n n n n n n n n a a a a a aa a a a a a a a + + + + + + + − − −−> + + + = = − 1 2 1 2 3 1 1 1n n n aa a ana a a a+ + + + + < − + { }na 12M a= 1n 1 1 12na a+ > 1 1 1 2 1 2 3 1 1 2 n n aa a na a a + + + + < − { }na 1 1na + 1 2na + 1 3na + 2n ( )1 1 2 1 1 2 1 2 2 1 2 3 1 1 2 n n n n n n a a a n na a a + + + + + + + + < − − 4018n 则 . 即存在正整数 ，使得 成立. ………………………………………14 分 说明：其它正确解法按相应步骤给分. 湖北省黄冈中学高考数学模拟考试 6 本试卷满分共 150 分，考试时间 120 分钟 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1．直线 的倾斜角是（ ） A． B． C． D． 2．已知 为平面，命题 p：若 ，则 ；命题 q：若 上不共线的三点到 的距离相等，则 ．对以上两个命题，下列结论中正确的是（ ） A．命题“p 且 q”为真 B．命题“p 或 ”为假 C．命题“p 或 q”为假 D．命题“ ”且“ ”为假 3. 某学校共有 2009 名学生，将从中选派 5 名学生在某天去国家大剧院参加音乐晚会，若采用以下 方法选取：先用简单随机抽样从 2009 名学生中剔除 9 名学生，再从 2000 名学生中随机抽取 5 名，则其中学生甲被选取的概率是（ ） A． B． C． D． , ,α β γ ,βα ⊥ β γ⊥ //α γ α β βα // q¬ p¬ q¬ 4018 4018 1 2 1 2 1 4018 4017 2 3 1 1 1 1 2 2 2 n n aa a n n n n na a a +      + + + < − + − − + + − −            4018 2009n= − 4018m n= 1 2 2 3 1 2009m m maa a a a a + −+ + + < 013 =++ yx 6 π 3 π 3 2π 6 5π 5 2009 1 2009 1 2000 1 400 4． 若不等式 的解集为 ，则实数 的值为（ ）. A． B． C．36 D． 5．已知 ﹑ 均为非零向量，条件 条件 的夹角为锐角，则 是 成立的 （ ） Ａ．充要条件 Ｂ．充分而不必要的条件 Ｃ．必要而不充分的条件 Ｄ．既不充分也不必要的条件 6．已知函数 为偶函数 ，其图像与直线 y=2 某两个交点的横坐标分别为 x1、 x2，若|x2-x1|的最小值为 ，则该函数在区间（ ）上是增函数． A． B． C． D． 7．函数 与 轴交点的个数是（ ） A、0 B、1 C、2 D、3 8．如果关于 x 的一元二次方程 中，a、b 分别是两次投掷骰子所得的点 数，则该二次方程有两个正根的概率 P=（ ） A． B． C． D． 9.已知 是等比数列， ，则 的取值范围是（ ） A. B. C. D. 10.　已知双曲线 的离心率为 e，左、右两焦点分别为 F1、F2，焦距为 ，抛物线 C 以 F2 为顶点，F1 为焦点,点 P 为抛物线与双曲线右支上的一个交点，若 a|PF2|＋ c|PF1|＝8a2，则 e 的值为 ( ) A. 3 B. 3 C. 2 D. 6 二、填空题：本大题共 5 小题，每小题 5 分，共 25 分. 把答案填在答题卡的相应位置上. 11 ． 若 ， 且 ， 则 实 数 的 值 为 __________． 12．如果把个位数字是 1，且恰有 3 个数字相同的四位数叫做“好数”， 那么在由 1，2，3，4 四个数字组成的有重复数字的四位数中 “好数”共有 个． 3 2x ax> + ( )4,b b 9 18 48 a b :p 0,a b⋅ >  :q a b 与 p q 2sin( )y xω θ= + (0 )θ π< < π ,2 4 π π − −   ,4 4 π π −   0, 2 π     3,4 4 π π     ( ) 2 3 1 2 3 x xf x x= + + + x 09)3(2 22 =+−−− bxax 18 1 9 1 6 1 18 13 { }na 4 1,2 52 == aa ( )1 2 2 3 1n na a a a a a n ∗ ++ +⋅⋅⋅+ ∈N [ )16,12 [ )16,8      3 32,8      3 32,3 16 2 2 2 2: 1( 0, 0)x yE a ba b − = > > 2c 6 6 2 210 6)1( xaxaxaamx +⋅⋅⋅+++=+ 1 2 6 63a a a+ +⋅⋅⋅+ = m 13．如图，O 是半径为 1 的球心，点 A、B、C 在球面上，OA、OB、 OC 两两垂直，E、F 分别为大圆弧 AB 与 AC 的中点，则点 E、 F 在该球上的球面距离是______． 14．已知 的最大值为 ． 15．直线 和圆 交于点 A、B，以 轴的正方向为始边，OA 为终边（O 是坐标 原点）的角为 ，OB 为终边的角为 ，那么 是 ． 三、解答题：本大题共 6 小题，共 75 分. 解答应写出文字说明、证明过程或演算步骤. 16． (本小题满分 12 分) 已知向量 ，定义函数 ，求函数 的最小正周期、单调递增区间． 17．（本题满分 12 分） 某地区试行高考考试改革：在高三学年中举行 5 次统一测试，学生如果通过其中 2 次测试即可 获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加 5 次测试. 假 设某学生每次通过测试的概率都是 ，每次测试通过与否互相独立. 规定：若前 4 次都没有通过测 试，则第 5 次不能参加测试． （1）求该学生恰好经过 4 次测试考上大学的概率； （2） 求该学生考上大学的概率． 1 3 yxyxz yx yx 42, 3 1)2()2( 22 22 +++=    ≤+ ≤−+− 则 2y x m= + 2 2 1x y+ = x α β sin( )α β+ ( ) ( )2sin ,cos , 3 cos ,2cosm x x n x x= =  ( ) ( )( )log 1 0, 1af x m n a a= − > ≠   ( )f x 18（本小题满分 12 分） 如图，在四棱锥 P-ABCD 中，底面 ABCD 为直角梯形，且 AB//CD，AB⊥AD，AD=CD=2AB=2．侧 面 为正三角形，且平面 PAD⊥平面 ABCD． （1）若 M 为 PC 上一动点，则 M 在何位置时，PC⊥平面 MDB？并加已证明； （2）若 G 为 的重心，求二面角 G-BD-C 大小． 19. (本小题满分 12 分) 已知函数 ， ， 的最小值恰好是方程 的三个根，其中 ． （1）求证： ； （2）设 是函数 的两个极值点．若 ， 求函数 的解析式． 20．（本题满分 13 分） 已知椭圆 ，直线 与椭圆交于 、 两点， 是线段 的中点，连接 并延长交椭圆于点 ． （1） 设直线 与直线 的斜率分别为 、 ，且 ，求椭圆的离心率． （2） 若直线 经过椭圆的右焦点 ，且四边 形 是平行四边形，求直线 斜率 的取值范围． | | 1y x= + 2 2 2y x x t= − + + 1 1( )2 ty x x −= + ( 0)x > 3 2 0x ax bx c+ + + = 0 1t< < 2 2 3a b= + 1,x 2x 3 2( )f x x ax bx c= + + + 1 2 2| | 3x x− = ( )f x PAD∆ PBC∆ 2 2 2 1( 2)x y aa + = ≥ l A B M AB OM C AB OM 1k 2k 1 2 1 2k k⋅ = − AB F OACB AB A B C D P 21． （本题满分 14 分） 已 知 点 ( N ) 顺 次 为 直 线 上 的 点 , 点 ( N )顺次为 轴上的点,其中 ,对任意的 N ,点 、 、 构成以 为顶点的等腰三角形． (Ⅰ)证明:数列 是等差数列； (Ⅱ)求证:对任意的 N , 是常数,并求数列 的通项公式； (Ⅲ)在上述等腰三角形 中是否存在直角三角形,若存在,求出此时 的值;若不存在,请说 明理由． 参考答案 1-5 DCACC 6-10 ABACA 11.1 或-3 12．12 13． 14．15 15． 16．解：因为 所以 故 …………6 分  ),,(,),,2(),,1( 2211 nn ynByByB ∈n ∗ 12 1 4 += xy )0,(),0,( 2211 xAxA  ),0,(, nn xA ∈n ∗ x )10(1 <<= aax ∈n ∗ nA nB 1+nA nB { }ny ∈n ∗ nn xx −+2 { }nx 1+nnn ABA a 3 π 4 5 − 22 3sin cos 2cos 3sin 2 cos2 1m n x x x x x= + = + +   ( ) ( )log 3 sin 2 cos 2 log 2sin 2 6a af x x x x   = + = +     π 2 2T = =π π 令 ，则 的单调递增的正值区间是 ， 单调递减的正值区间是 当 时，函数 的单调递增区间为 当 时，函数 的单调递增区间为 （注：区间为开的不扣 分）…………12 分 17．（本题满分 12 分） 解 ： （ Ⅰ ） 记 “ 该 学 生 恰 好 经 过 4 次 测 试 考 上 大 学 ” 的 事 件 为 事 件 A ， 则 ……6 分 （ Ⅱ ） 记 “ 该 生 考 上 大 学 ” 的 事 件 为 事 件 B ， 其 对 立 事 件 为 ， 则 ∴ ……12 分 18．解：（1）当 M 为 PC 的中点时，PC⊥平面 MDB．------------------1 分 事实上，连 BM，DM，取 AD 的中点 N，连 NB，NP． 因为 ，且平面 PAD 平面 ABCD，所以 PN⊥平面 ABCD． 在 中， ，所以 ，又 所以 ，又 ， 平面 MDB， 而 PD=DC=2，所以 ，所以 平面 MDB------------------6 分 （2）易知 G 在中线 BM 上，过 M 作 于 F，连 CF， 因为 平面 MDB，所以 ， 故 是二面角 G—BD—C 的平面角 ------------------9 分 在 中， ，所以 ，又 所以 ，故二面角 G—BD—C 的大小为 ----------------12 分 2 1 3 .1 2 1 4( ) 3 3 3 27P A C      = ⋅ ⋅ ⋅ = B 1 3 4 4 1 2 2 2 64 16 112( ) ( )( ) ( ) ( ) .3 3 3 3 243 81 243P B C= + = + = 112 131( ) 1 ( ) 1 .243 243P B P B= − = − = ( ) 2sin 2 6g x x = +   π ( )g x ( ),12 6k k k Z − + ∈   π ππ π ( )5,6 12k k k Z π ππ π + + ∈  0 1a< < ( )f x ( )5,6 12k k k Z + + ∈  π ππ π 1a > ( )f x ( ),12 6k k k Z − + ∈   π ππ π PN AD⊥ ⊥ Rt PNB∆ 3, 2PN NB= = 5PB = 5BC = BN PC⊥ MD BM M= ,MD BM ⊂ DM PC⊥ PC ⊥ MF BD⊥ PC ⊥ CF BD⊥ MFC∠ Rt BDC∆ 5, 2, 5BD DC BC= = = 4 5 5CF = 2CM = 10sin 4MFC∠ = 10arcsin 4 19．21.解：（1）三个函数的最小值依次为 ， ， 由 ，得 ∴ ， 故方程 的两根是 ， ． 故 ， ． ， 即 ∴ ．………………6 分 （2）①依题意 是方程 的根， 故有 ， ， 且△ ，得 ． 由 ……………9 分 ；得， ， ． 由（1）知 ，故 ， ∴ ， ∴ ．………………………12 分 20．（1）解法一：设 ， , ,则 两式相减，得： 又 ， ， ， 1 1 t+ 1 t− (1) 0f = 1c a b= − − − 3 2 3 2( ) ( 1)f x x ax bx c x ax bx a b= + + + = + + − + + 2( 1)[ ( 1) ( 1)]x x a x a b= − + + + + + 2 ( 1) ( 1) 0x a x a b+ + + + + = 1 t− 1 t+ 1 1 ( 1)t t a− + + = − + 1 1 1t t a b− ⋅ + = + + 2 2( 1 1 ) ( 1)t t a− + + = + 22 2( 1) ( 1)a b a+ + + = + 2 2 3a b= + 1 2,x x 2'( ) 3 2 0f x x ax b= + + = 1 2 2 3 ax x+ = − 1 2 3 bx x = 2(2 ) 12 0a b= − > 3b < 2 2 1 2 1 2 1 2 2 3 2 3| | ( ) 4 3 3 a b bx x x x x x − −− = + − = = 2 3 3 b− 2 3 = 2b = 2 2 3 7a b= + = 1 1 ( 1) 0t t a− + + = − + > 1a < − 7a = − ( 1) 7 3c a b= − + + = − 3 2( ) 7 2 7 3f x x x x= − + + − ( )1 1,A x y ( )2 2,B x y ( )0 0,C x y 2 21 12 2 22 22 1 1 x ya x ya  + =  + = ( )( ) ( )( )1 2 1 2 1 2 1 22 0x x x x y y y ya + − + + − = 1 2 0 2 x xx += 1 2 0 2 y yy += 1 2 1 1 2 y yk x x −= − 0 2 0 yk x = 可得 ……………………………………（5 分） 解法二：设 ， , ,，直线 ① ， ，又 由条件： 即 ……………………………………………………………………（5 分） （2）由①及 ，可知 代入椭圆方程，得 ………………………………………………………………………（10 分） 又 …………………………………………………（13 分） 21.解: (Ⅰ)依题意有 ,于是 . 所以数列 是等差数列. ………………….2 分 (Ⅱ)由题意得 ,即 , ( ) ① 所以又有 . ② ………4 分 由② ①得 , 可知 都是等差数列.那么得 , 2 2 1 2 1 1 222 2k k a ea ⋅ = − = − ⇒ = ⇒ = ( )1 1,A x y ( )2 2,B x y ( )0 0,C x y : ( 0)l x my n m= + ≠ ( )2 2 2 2 2 2 2 2 1 0x my n m a y mny x a y a = + ⇒ + + − = + = ⇒ 1 2 0 2 y yy += 2 2 mn m a = − + 2 0 0 2 2 a nx my n m a = + = + 2 2 1k ma ⇒ = − 1 1k m = 1 2 2 1k k a ⇒ = − ( )2 2 2 2 2 1 2 2 1 2 22 bk k a b a ca = − ≥ − ⇒ ≥ = − 2 22 2a e= ⇒ = n c= 2 2 2 2 2 2 2,a c mcC m a m a  − + +  2 2 24c m a= + 2 2 1c a= − 2a ≥ 0m ≠ 2 2 2 1 1 1 3 4 8ABk m a ⇒ = = ≤− 2 2,0 0,4 4ABk    ⇒ ∈ −        12 1 4 += nyn 4 1 1 =−+ nn yy { }ny nxx nn =+ + 2 1 nxx nn 21 =+ + n ∗∈ N )1(212 +=+ ++ nxx nn − 22 =−+ nn xx  ,,,;,,, 642531 xxxxxx 22)1(2112 −+=−+=− akkxx k . ( 故 …………8 分 (Ⅲ)当 为奇数时, ,所以 当 为偶数时, 所以 作 轴,垂足为 则 ,要使等腰三角形 为直角三角形,必 须且只需 . 当 为奇数时,有 ,即 . ① 当 时, ;当 时, ;当 , ①式无解. 当 为偶数时,有 ,同理可求得 . 综上所述,上述等腰三角形 中存在直角三角形,此时 的值为 或 或 . ……………………..14 分 湖北省黄冈中学高考数学模拟考试 7 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分，在每小题给出的四个选项中，只有一项是 满足题目要求的。 1. 若 sin2θ－1＋i( cosθ＋1)是纯虚数（其中 i 是虚数单位），且θ∈［0,2π)，则θ的值 A B C D 或 2. 设集合 ， ， , 若 ，则 b = c 的概率是 A B C D akkakxx k −=−+−=−+= 2)1(22)1(222 ∈k ∗N ) 1 ( (n n a nx n a n + −=  − 为奇数） 为偶数）. n )0,1(),0,1( 1 anAanA nn −+−+ + );1(21 aAA nn −=+ n ),0,(),0,( 1 anAanA nn +− + ;21 aAA nn =+ xCB nn ⊥ ,nC 12 1 4 += nCB nn 1+nnn ABA nnnn CBAA 21 =+ n )12 1 4(2)1(2 +=− na na 31112 −= 1=n 3 2=a 3=n 6 1=a 5≥n n 1312 += na 12 7=a 1+nnn ABA a 3 2 6 1 12 7 2 4 π 4 3π 4 5π 4 π 4 3π }1,{bP = }2,1,{cQ = QP ⊆ }9,8,7,6,5,4,3,2{, ∈cb 8 1 4 1 2 1 8 3 3. .向量 =( )， 是直线 y=x 的方向向量，a =5,则数列 的前 10 项的和 A 50 B 100 C 150 D 200 4. , 则 被3除的余数是 A.0 B.1 C.2 D.不能确定 5. 已知 x，y 满足条件 Error! 则 z＝ x＋y＋2 x＋3 的最小值（ ） A 4 B C D - 6.已知函数 的反函数为 ，在 上的导函数为 ， 则 = A． B． C． D． 7．已知函数 ，动直线 与 、 的图象分别 交于点 、 ， 的取值范围是 A．[0，1] B．[0，2] C．[0， ] D．[1， ] 8.已知两个不相等的实数 满足以下关系式： ，则连接 A 、 B 两点的直 线与圆心在原点的单位圆的位置关系是 ． A 相离 B 相交 C 相切 D 不能确定 9. 直线 MN 与双曲线 C: 的左右支分别交与 M、N 点，与双曲线 C 的右准线相交于 P 点，F 为右焦点，若 ,又 ( ),,则实数 的值为 A B 1 C 2 D 10. 已知 为定义在 上的可导函数,且 对于 恒成立,则 A. , B. , C. , 1 2 2 log ( ) ( 1) x f x x =   − ( 1) ( 1) x x ≥ < 1( )f x− ( ,1) (1, )−∞ +∞ ( )f x′ 1(4) ( 1)f f− ′+ − 6− 1 1− 5− V n nn n a aaa 2,2 2 1 1 + + − V 1 { }na 2010 2010 2 210 2010)42( xaxaxaax ++++=+  2010420 aaaa ++++  6 13 3 1 3 2 ( ) sin cos , ( ) 2sinf x x x g x x= + = x t= ( )f x ( )g x P Q | |PQ 2 2 a b、 2 04a sin a cos πθ θ⋅ + ⋅ − = ， 2 04b sin b cos πθ θ⋅ + ⋅ − = ( )2a ,a ( )2b ,b 12 2 2 2 =− b y a x FNFM 2= PMNP λ= R∈λ λ 2 1 3 1 )(xf ),( +∞−∞ )()( xfxf ′< Rx ∈ )0()2( 2 fef ⋅> )0()2010( 2010 fef ⋅> )0()2( 2 fef ⋅< )0()2010( 2010 fef ⋅> )0()2( 2 fef ⋅> )0()2010( 2010 fef ⋅< 数学（理工农医类）试题第 2 页（共 4 页） D. , 二、填空题：本大题共 5 小题，每小题 5 分，共 25 分.请将答案填在答题卡对应题号的位置上,一题 两空的题,其答案按先后次序填写. 11. 设函数 f(x)= ，要使 f(x)在（-∞，+∞）内连续，则 =______ 12. 已知随机变量 服从正态分布，且方程 x +2x+ =0 有实数解得概率为 ，若 P（ ） =0.8，则 P（0 ）=___________ 13. 将 A、B、C、D、E 五种不同的文件放入一排编号依次为 1、2、3、4、5、6 的六个抽屉内，每 个抽屉至多放一种文件.若文件 A、B 必须放入相邻的抽屉内，文件 C、D 也必须放相邻的抽屉内， 则文件放入抽屉内的满足条件的所有不同的方法有 种． 14.已知点 M 是抛物线 y =4x 的一点，F 为抛物线的焦点，A 在圆 C:(x-4) +(y-1) =1 上，则 的最小值为__________; 15. ． 如 图 , 在 三 棱 锥 中 , 、 、 两 两 垂 直 , 且 . 设 是 底 面 内 一 点 , 定 义 , 其中 、 、 分别是三棱锥 、 三棱锥 、三棱锥 的体积.若 ,且 恒成立,则正实数 的最小值为________. 三、解答题：本大题共 6 小题，共 75 分。解答应写出文字说明、证明过程或演算步骤。 16. 已知锐角 的三内角 A、B、C 的对边分别是 （1）求角 A 的大小； （2）求 的值。 17. 如图，在 中， ，斜边 ． 可以通过 以直线 为轴旋转得到，且二面角 是直二面角．动点 的斜边 上． a P ABC− PA PB PC 3, 2, 1PA PB PC= = = M ABC ( ) ( , , )f M m n p= m n p M PAB− M PBC− M PCA− 1( ) ( , , )2f M x y= 1 8a x y + ≥ a Rt AOB△ π 6OAB∠ = 4AB = Rt AOC△ Rt AOB△ AO B AO C− − D AB )0()2( 2 fef ⋅< )0()2010( 2010 fef ⋅<    ≥+ <−− )0( )0(11 2 xxa xx x ξ 2 ξ 2 1 ξ 2≤ ≤ ξ 2≤ 2 2 2 MFMA + ABC∆ .3tan)(,,, 222 bcAacbcba =−+且 )]10tan(31[)10sin( °−−⋅°+ AA 第 15 题 M C B A P （1）求证：平面 平面 ； （2）当 为 的中点时，求异面直线 与 所成角的大 小； （3）求 与平面 所成角的最大值． 18. 某地区试行高考考试改革：在高三学年中举行 5 次统一测试， 学生如果通过其中 2 次测试即可获得足够学分升上大学继续学 习，不用参加其余的测试，而每个学生最多也只能参加 5 次测试. 假设某学生每次通过测试的概率 都是 ，每次测试通过与否互相独立. 规定：若前 4 次都没有通过测试，则第 5 次不能参加测试. (Ⅰ) 求该学生考上大学的概率. (Ⅱ) 如果考上大学或参加完 5 次测试就结束，记该生参加测试的次数为ξ，求变量ξ的分布列及 数学期望 Eξ。 19. 已知二次函数 g（x）对任意实数 x 都满足 ，且 ．令 ． （1）求 g(x)的表达式； （2）设 ， ， 证明:对任意 x ,x ，恒有 20. 如图，已知直线 的右焦点 F，且交椭圆 C 于 A，B 两点，点 A，F，B 在直线 上的射影依次为点 D，K，E， COD ⊥ AOB D AB AO CD CD AOB 1 3 ( ) ( ) 21 1 2 1g x g x x x− + − = − − ( )1 1g = − ( )1 9( ) ln ( , 0)2 8f x g x m x m x= + + + ∈ >R 1 em< ≤ ( ) ( ) ( 1)H x f x m x= − + 1 2 [ ]m,1∈ 1 2| ( ) ( ) | 1.H x H x− < )0(1:1: 2 2 2 2 >>=++= bab y a xCmyxL 过椭圆 2: axG = O C A D B （1）已知抛物线 的焦点为椭圆 C 的上顶点。 ①求椭圆 C 的方程； ②若直线 L 交 y 轴于点 M，且 ， 当 m 变化时，求 的值； （2）连接 AE，BD，试探索当 m 变化时，直线 AE、BD 是否相交 于一定点 N？若交于定点 N，请求出 N 点的坐标并给予证 明；否则说明理由. 21. 已知数列 的首项 ， ， ． （1）求 的通项公式； （2）证明：对任意的 ， ， ； （3）证明： ． 参考答案 1-10 ACACC DCBAA 11． 12 ．0.6 13． 96 14．4 15 ．1 16. 解：（1）由已知条件及余弦定理得 ∴ .∵ ……………………6 分 （2） = sin70 =2sin70 ==－ =－1 ….12 分 17.解：（I）由题意， ， ， 是二面角 的平面角， { }na 1 3 5a = 1 3 2 1 n n n aa a+ = + 1 2n = ，， { }na 0x > 2 1 1 2 1 (1 ) 3n na xx x  − − + +  ≥ 1 2n = ，， 2 1 2 1n na a a n + + + > + CO AO⊥ BO AO⊥ BOC∴∠ B AO C− − yx 342 = BFMBAFMA 21 , λλ == 21 λλ + 2 1 3 sin 3tan , ,2 cos cos 2cos bc AA bc A A A = ∴ = 3sin 2A = (0, )2A π∈ , .3A π=故 )50cos 50sin31(70sin)]10tan(31)[10sin( ° °−°=°−−°+ AA    50cos 50sin350cos −    50cos )5030sin( −   40sin 20cos20sin2 又 二面角 是直二面角， ，又 ， 平面 ，又 平面 ． 平面 平面 ． --------4 分 （II）作 ，垂足为 ，连结 ，则 ， 是异面直线 与 所成的角． - -------------------------5 分 在 中 ， ， ， ． 又 ． 在 中， ． ----------7 分 异面直线 与 所成角的大小为 ． ----------------------8 分 （ III ） 由 （ I ） 知 ， 平 面 ， 是 与 平 面 所 成 的 角 ， 且 ．当 最小时， 最大………………10 分 这时， ，垂足为 ， ， ， 与平面 所成角的最大值为 ．- ----------------------12 18. 解 ： （ Ⅰ ） 记 “ 该 生 考 上 大 学 ” 的 事 件 为 事 件 A ， 其 对 立 事 件 为 ， 则 ∴ ……6 分 （Ⅱ）该生参加测试次数ξ的可能取值为 2，3，4，5. ， ， ， 故ξ的分布列为： ……12 分 19.解 （1）设 ，于是 所以 又 ，则 ．所以 . ……………5 分  B AO C− − CO BO∴ ⊥ AO BO O=  CO∴ ⊥ AOB CO ⊂ COD ∴ COD ⊥ AOB DE OB⊥ E CE DE AO∥ CDE∴∠ AO CD Rt COE△ 2CO BO= = 1 12OE BO= = 2 2 5CE CO OE∴ = + = 1 32DE AO= = ∴ Rt CDE△ 5 15tan 33 CECDE DE = = = ∴ AO CD 15arctan 3 CO ⊥ AOB CDO∴∠ CD AOB 2tan OCCDO OD OD = = OD CDO∠ OD AB⊥ D 3=⋅= AB OBOAOD 3 32tan =∠CDO CD∴ AOB 2 3arctan 3 A .243 112 81 16 243 64)3 2()3 2()3 2)(3 1()( 431 4 =+=+= CAP 112 131( ) 1 ( ) 1 .243 243P A P A= − = − = 21 1( 2) 3 9P ξ      = = = 1 2 1 2 1 4( 3) . . .3 3 3 27P Cξ = = = 2 1 4 3 1 2 1 2 4 16 28( 4) ( )3 3 3 3 27 81 81P Cξ      = = ⋅ ⋅ ⋅ + = + = 3 1 4 1 2 32( 5) .3 3 81P Cξ            = = ⋅ ⋅ = .81 326 81 32581 28427 439 12 =×+×+×+×=ξE ( ) 2g x ax bx c= + + ( ) ( ) ( ) ( )2 21 1 2 1 2 2 1 2g x g x a x c x− + − = − + = − − ， 1 2 1. a c  =  = − ， ( )1 1g = − 1 2b = − ( ) 21 1 12 2g x x x= − − （2）因为对 ， 所以 在 内单调递减. 于是 …………………8 分 记 ，则 所以函数 在 是单调增函数， 所以 ，故命题成立. ………………… 12 分 20. 解：（1）易知 ， …………………3 分 设 …………………………5分 又由 同理 ……………………………………8分 （3） ,先探索，当m=0时，直线L⊥ox轴，则ABED为矩形，由对称性知，AE 与BD相交FK中点N，且 猜想：当m变化时，AE与BD相交于定点 ……………………9分 证明：设 [1 ]x m∀ ∈ ， ( 1)( )( ) 0x x mH x x − −′ = ≤ ， ( )H x [1, ]m 2 1 2 1 1| ( ) ( ) | (1) ( ) ln .2 2H x H x H H m m m m− ≤ − = − − 2 1 2 1 1 1 3| ( ) ( ) | 1 ln 1 ln 0.2 2 2 2H x H x m m m m m m − < ⇐ − − < ⇔ − − < 1 3( ) ln (1 e)2 2h m m m mm = − − < ≤ ( )2 2 1 1 3 3 1 1 1( ) 02 2 3 32h' m m mm = − + = − + > ， 1 3( ) ln2 2h m m m m = − − (1 e]， ( )( )e 3 e 1e 3( ) (e) 1 02 2e 2eh m h − +≤ = − − = < )0,1(,33 2 Fbb 又=∴= 41 222 =+==∴ cbac 134 22 =+∴ yxC的方程为椭圆 )1,0( mMyl −轴交于与    =−+ += 01243 1),(),,( 222211 yx myxyxByxA 由 0)1(144096)43( 222 >+=∆=−++∴ mmyym (*)3 211 21 m yy =+∴ ),1()1,( 111111 yxmyxAFMA −−=+∴= λλ 1 1 11 my −−=∴λ 2 2 11 my −−=λ 3 8 3 22)11(12 21 21 −=−−=+−−=+∴ yym λλ )0,(),0,1( 2akF = )0,2 1( 2 +aN )0,2 1( 2 +aN ),(),,(),,(),,( 1 2 2 2 2211 yaDyaEyxByxA 当m变化时首先AE过定点N A、N、E三点共线， 同理可得B、N、D三点共线 ∴AE与BD相交于定点 ……………………13分 21.解法一：（Ⅰ） ， ， ， 又 ， 是以 为首项， 为公比的等比数列． ………3 分 ， ． ……………………4 分 （Ⅱ）由（Ⅰ）知 ， ……………………5 分 ， 原不等式成立．………………8 分 1 3 2 1 n n n aa a+ = + 1 1 2 1 3 3n na a+ ∴ = + 1 1 1 11 13n na a+  ∴ − = −    1 21 3na − = 1 1 na  ∴ −    2 3 1 3 ∴ 1 1 2 1 21 3 3 3n n na −− = ⋅ = 3 3 2 n n na∴ = + 3 03 2 n n na = >+ 2 1 1 2 1 (1 ) 3n xx x  − − + +   2 1 1 2 1 11 (1 ) 3n xx x  = − + − − + +   2 1 1 1 (1 )1 (1 ) n xx x a  = − − + + +   2 1 1 2 (1 ) 1na x x = − ⋅ ++ + 21 1 1 n n n a aa x  = − − + +  na≤ ∴ 2 1, 2 1 )1(0)1(4 0)1(2)( 0 1 2 2 1 2 1 22222 2222222 222222 a yK mya yK abmaba abymbymba bayaxb myx ENAN − −= −− −= >>−+=∆ =−+++    =−+ += 又 即   )2 1(2 1 )(2 1 1 22 2121 2 myaa ymyyya KK ENAN −−− −+− =−而 )0)()1( )1()2(2 1)(2 1( 222 222 222 22 222 22 2121 2 =+ −⋅−= + −⋅−+−⋅−=−+− bma mbmba bma abmbma mbaymyyya  ∴=∴ ENAN KK )0,2 1( 2 +aN （Ⅲ）由（Ⅱ）知，对任意的 ，有 ． ……………………10 分 取 ，…………12 分 则 ． 原不等式成立． ……………………14 分 注：（Ⅱ）设 ，用导数求得当 时， 取得最大值为ａｎ．参 照本标准给分。 湖北省黄冈中学高考数学模拟考试 8 参考公式：锥体的体积公式 ，其中 是锥体的底面积， 是锥体的高． 柱体的体积公式 V=Sh , 其中 是柱体的底面积， 是柱体的高 如果事件 、 互斥，那么 ． 如果事件 、 相互独立，那么 ． 如果事件 在一次试验中发生的概率是 ，那么在 次独立重复试验中恰好发生 次的概率 ． 一．选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项是符 合题目要求的 0x > 1 2 2 2 2 2 1 1 2 1 1 2 1 1 2 1 (1 ) 3 1 (1 ) 3 1 (1 ) 3n na a a x x xx x x x x x      + + + − − + − − + + − −     + + + + + +      ≥ 2 2 1 2 2 2 1 (1 ) 3 3 3n n nxx x  = − + + + − + +   ∴ 2 2 111 2 2 2 1 13 3 113 3 3 31 3 n n nx n nn  −     = + + + = = −       −    2 2 1 2 11 1 111 1 33 n nn n n na a a nn n + + + = > +  + −+ −    ≥ ∴ 2 1 1 2( ) 1 (1 ) 3nf x xx x  = − − + +   2 3nx = ( )f x 1 3V Sh= S h S h A B ( ) ( ) ( )P A B P A P B+ = + A B ( ) ( ) ( )P A B P A P B⋅ = ⋅ A p n k ( ) ( )C 1 n kk k n nP k p p −= − 1．已知α、β都是第二象限角，且 cosα>cosβ，则（　） A．α<β B．sinα>sinβ C．tanα>tanβ D．cotα x 1 3 1 2 1 0 1,a< < (1 ) (1 )log (1 ) log (1 ) 2a aa a+ −− + + > (1 ) (1 )log (1 ) log (1 )a aa a+ −− < + (1 ) (1 ) (1 ) (1 )log (1 ) log (1 ) log (1 ) log (1 )a a a aa a a a+ − + −− + + < − + + (1 ) (1 ) (1 ) (1 )log (1 ) log (1 ) log (1 ) log (1 )a a a aa a a a+ − + −− − + > − − + 2( ) log ( 3)( 0 1)af x x ax a a= − + > ≠且 1x 2x 221 axx ≤< 0)()( 21 >− xfxf a )3,1()1,0(  )3,1( )32,1()1,0(  )32,1( ,)1(,3)1( jmibiima −+=−+= )()( baba −⊥+ )(xf 1=x 21 )(lim 1 =−→ x xf x )1(f 1− 0 1 2 2xy = { }4,1 A．7 个 B．8 个 C．9 个 D．10 个 10．如图，在 中， ，AC、BC 边上的高分别为 BD、AE，则以 A、B 为焦点，且过 D、E 的椭圆与双曲线的离心率的倒数和为 （ ） A． B． C． D． 11．给出下列命题中 ① 向量 满足 ，则 的夹角为 ； ② ＞0，是 的夹角为锐角的充要条件； ③ 将函数 y = 的图象按向量 =(－1,0)平移，得到的图象对应的函数表达式为 y = ； ④ 若 ，则 为等腰三角形； 以上命题正确的个数是（ ） A．4 个 B．1 个 C．3 个 D．2 个 12．如图，在正三棱锥 S—ABC 中，M、N 分别为棱 SC、BC 的中点，并且 AM MN，若侧棱 长 SA= ，则正三棱锥 S—ABC 的外接球的表面积为 （ ） A．9 B．12 C．16 D．32 二．填空题：本大题共 4 小题，每小题 4 分，共 16 分． 13．一个几何的三视图如图所示：其中，正视图中△ABC 的边长是 2 的正三角形，俯视图为正 六边形，那么该几何体几的体积为 . ABC∆ 030=∠=∠ CBACAB 3 1 32 2 a b 、 a b a b= = −    与a a b+   030 a ⋅ b a b 、 1−x a x )( →−→− + ACAB 0)( =−⋅• →−→− ACAB ABC∆ ⊥ 3 π π π π E D C A B 1 4 1 1,2 4 3 3 3, ,4 8 1 6  14．下表给出一个“直角三角形数阵”：满足每一列成等 差数列，从第三行起，每一行的数成等比数列，且每一行 的公比相等，记第 行第 列的数为 为 . 15．如右图，E、F 分别是正方体的面 ADD1A1、面 BCC1B1 的中心，则四边形 BFD1E 在该正方体的面上的射影可能是　　　　　.（要求：把可能的图的序号 都填上） 16．如下图，给出了一个程序框图,其作用是输入 的值,输出相应的 的值,若要使输入的 的值与 输出的 的值相等,则这样的 的值的集合为 . 三．解答题：本大题共 6 小题，共 74 分． 17．（本小题满分 12 分）已知复数 , , i j ( )*, ,ija i j i j N≥ ∈ x y x y x 开始 y输出 结束 2x ≤ ？ x输入 2y x= 5x ≤ ？ 2 3y x= − 1y x = 1图 是 否 是 否 1 3sin 2 z x iλ= + 2 ( cos2 ) ( , , ,)z m m x i m x Rλ= + − ∈ ○1 ○2 ○3 ○4 A B D C F A1 C1D1 且 ．（Ⅰ）若 且 ，求 的值；（Ⅱ）设 ＝ ，求 的最小正周期 和单调增区间． 18．（本小题满分 12 分）已知 是数列{ }的前 项和， (1)分别计算 的值； (2)证明：当 ≥1 时， ≥1 2，并指出等号成立条件； (3)利用（2）的结论，找出一个适当的 ∈N，使得 ＞2008； (4)是否存在关于正整数 的函数 ，使得 对于大于 1 的正整数 都成立？证明你的结论。 19．（本小题满分 12 分）在四棱锥 中， , , 底面 , ，直线 与底面 成 角，点 分别是 的中点． （１）求二面角 的大小； （２）当 的值为多少时， 为直角三角形. 20．（本小题满分 12 分）一种电脑屏幕保护画面，只有 符 号 “○”和“×”随机地反复出现，每秒钟变化一次，每次变化只出现“○”和“×”之一，其中出 现“○”的概率为 p，出现“×”的概率为 q，若第 k 次出现“○”，则记 ；出现“×”，则记 ，令 （I）当 时，记 ，求 的分布列及数学期望； （II）当 时，求 的概率. 21．（本小题满分 13 分）一束光线从点 出发，经直线 上一点 反 射后，恰好穿过点 ．（Ⅰ）求点 关于直线 的对称点 的坐标；（Ⅱ）求以 、 为 焦点且过点 的椭圆 的方程；（Ⅲ）设直线 与椭圆 的两条准线分别交于 、 两点，点 为 线段 上的动点，求点 到 的距离与到椭圆 右准线的距离之比的最小值，并求取得最小值 时点 的坐标． 1 2z z= 0λ = 0 x π< < x λ ( )f x ( )f x nS n 1 n 482412 ,, SSSSSS −−− n 122 −− nn SS T TS n )(nf )1)((121 −=+⋅⋅⋅++ − nn SnfSSS n ABCDP − ABAD ⊥ ABCD // ⊥PD ABCD 2= AD AB PA ABCD 060 NM , PBPA, DMNP −− AB CD CDN∆ 1=ka 1−=ka .21 nn aaaS +++=  2 1== qp || 3S=ξ ξ 3 2,3 1 == qp )4,3,2,1(028 =≥= iSS i且 )0,1(1 −F 032: =+− yxl P )0,1(2F 1F l 1F′ 1F 2F P C l C A B Q AB Q 2F C Q 22．（本小题满分 13 分）设 是满足不等式 的自然数 的个 数 ， 其 中 ．（Ⅰ ） 求 的 值 ； ( Ⅱ ) 求 的 解 析 式 ； （ Ⅲ ） 记 ，令 ，试比较 与 的大小． 备选题：已知函数 . （1）求函数 在区间 （ 为自然对数的底）上的最大值和最小值； （2）求证：在区间 上，函数 的图象在函数 的图象的下方； （3）求证： ≥ . 参考答案： B B A AAD D DC A DA 1．在第二象限角内通过余弦函数线 cosα>cosβ找出α、β的终边位置关系，再作出判断，得 B。 2．取 f(x)= －x，逐项检查可知①④正确。故选 B。 3． 为抛物线 的内部（包括周界）， 为动圆 的内部（包括周界）.该题 的几何意义是 为何值时，动圆进入区域 ，并被 所覆盖. 是动圆圆心的纵坐标，显然结论应是 ，故可排除 ，而当 时， （可验证点 到抛物线上点的最小距离为 ）.故选 . 4．具有伙伴关系的元素组有－1，1， 、2， 、3 共四组，它们中任一组、二组、三组、四 组均可组成非空伙伴关系集合，个数为 C + C + C + C =15, 选 A． 5．取满足题设的特殊数值 a= , ， 0> ,检验不等式(B),(C),(D)均不成立,选 (A). ( )f k 2 23 ( ) 2 ( ) 0 x g k x g k− ⋅ ⋅ + ≤ x 1 *( ) 2 ( )kg k k N−= ∈ (1)f ( )f k 1 ( ) n n i S f i = = ∑ ( )∗∈−+= NnnnPn 12 nS nP 21( ) ln 12f x x x= + − ( )f x [1, ]e e (1, )+∞ ( )f x 32( ) 3g x x= [ '( )] '( )n nf x f x− 2 2n − ( )n N ∗∈ E 2y x= F ( )22 1x y a+ − = a E E a ( )a c c R+≥ ∈ ( ) ( ),B D 1a = .E F F≠ ( )0,1 3 2 ( )A 2 1 3 1 1 4 2 4 3 4 4 4 2 1 13 2log2 1log)1(log 2 3 2 3)1( −=<=−+ aa 12log2 3log)1(log 2 1 2 1)1( −=>=+− aa 6．“对任意的 x1、x2，当 时， ”实质上就是“函数单调递减”的 “伪装”，同时还隐含了“ 有意义”。事实上由于 在 时递减，从而 由此得 a 的取值范围为 。故选 D。 7． ∵ ， ∴ ∴ ， 而 i，j 为互相垂直的单位向量，故可得 ∴ 。故选 8．特殊值法, 令 , 得 . 9．由题意知同族函数的定义域非空, 且由 中的两个(这里 和 中各有一 个), 或三个, 或全部元素组成, 故定义域的个数为 。 10．设 , 则在椭圆中, 有 , , 而在双曲线中, 有 , , ∴ 11．对于 ① 取特值零向量错误，若前提为非零向量由向量加减法的平行四边形法则与夹角的概 念正确； 对②取特值夹角为直角错，认识数量积和夹角的关系，命题应为 ＞0，是 的夹角为锐 角的必要条件； 对于③，注意按向量平移的意义，就是图象向左移 1 个单位，结论正确； 对于④；向量的数量积满足分配率运算，结论正确； 故选 D. 12． 三棱锥 S—ABC 正棱锥， SB AC（对棱互相垂直） MN AC 又 MN AM 而 AM AC=A， MN 平面 SAC 即 SB 平面 SAC ASB= BSC= ASC= ，将此三棱锥补成正方体，则它们有相同的外接球 2R= ， R= ， S= = =9 ，故选 A． 13． 221 axx ≤< 0)()( 21 >− xfxf )(xf 3)( 2 +−= axxxg 2 ax ≤    > > .0)2( ,1 ag a )32,1( .)2(,)4()2( jmmibajmimba +−=−−++=+ )()( baba −⊥+ 0)()( =−⋅+ baba 0)4)(2()]4()2([)2( 222 =−+−⋅−++−++ jmmjimmmjmm ,0)4)(2()2( =−+−+ mmmm 2−=m ( )D )1)(1()( +−= xxxf 2)1( =f 2,1,2,1 −− 1,1− 2,2− 911 2 1 2 1 2 1 2 =++ CCCC cAB 2|| = acc 23 =+ 2 311 1 +== c a e acc 23 =− 2 131 2 −== c a e 32 13 2 3111 21 =−++=+ ee a ⋅ b a b 、  ∴ ⊥ ∴ ⊥  ⊥  ∴ ⊥ ⊥ ∴ ∠ ∠ ∠ 90 ∴ 3 3⋅ ∴ 3 2 ∴ 24 Rπ 234 ( )2 π ⋅ π 11 3 33, 1, 1 6 33 4 2h a V= = = × × × × = 14． ； 15．因为正方体是对称的几何体，所以四边形 BFD1E 在该正方体的面上的射影可分为：上下、 左右、前后三个方向的射影，也就是在面 ABCD、面 ABB1A1、面 ADD1A1 上的射影. 四边形 BFD1E 在面 ABCD 和面 ABB1A1 上的射影相同，如图○2 所示； 四边形 BFD1E 在该正方体对角面的 ABC1D1 内，它在面 ADD1A1 上的射影显然是一条线段，如 图○3 所示. 故应填○2 ○3 . 16．解：依题意得 ,或 ,或 ,解得 ,或 , . 17．解：（Ⅰ）∵ ∴ ∴ -----------------2 分 若 则 得 ----------------------------4 分 ∵ ∴ 或 ∴ -------------------------------------6 分 （Ⅱ）∵ ＝ ----------------------------------9 分 ∴函数的最小正周期为 T=π-----------------------------------------10 分 由 得 ∴ 的单调增区间 .----------------12 分 18．(1) ＝ 1 2， ＝ 1 3＋ 1 4＝ 7 12， ＝ 1 5＋ 1 6＋ 1 7＋ 1 8＝ 168＋140＋120＋105 840 ＝ 533 840。 …………2 分 ( )81 11 1 1 78 1 2,4 4 4a a= + − × = + = 4 85 81 1 1 122 16 8a a  = × = × =   ( )1 11 11 ,4 4i ia a i= + − × = 1 1 1 1 1 1 1 2 4 2 2 j j j ij i ia a i − − +     = × = × = ×           2 2x x x ≤  = 2 5 2 3 x x x < ≤  − = 1 5 x x x >  = 0x = 1x = 3x = 1 2z z= 3sin 2 cos2 x m m xλ  = = − 3sin 2 cos2x xλ −＝ 0λ = 3sin 2 cos2 0x x− = 3tan 2 3x = 0 ,x π< < 0 2 2x π∴ < < 2 ,6x π= 72 ,6x π= 7,12 12x π π= 3 1( ) 3sin 2 cos2 2( sin 2 cos2 )2 2f x x x x xλ = = − = − 2(sin 2 cos cos2 sin )6 6x x π π− 2sin(2 )6x π= − 2 2 2 ,2 6 2k x k k Z π π ππ π− ≤ − ≤ + ∈ ,6 3k x k k Z π ππ π− ≤ ≤ + ∈ ( )f x [ , ],6 3k k k Z π ππ π− + ∈ 12 SS − 24 SS − 48 SS − (2)当 ≥1 时， ＝ 1 2n－1＋1＋ 1 2n－1＋2＋…＋ 1 2n(共 2n－1 项) ≥ ×2n－1＝ 1 2，当且仅当 ＝1 时，等号成立。 …………4 分 (3)由于 ＝1，当 ≥1 时， ≥ 1 2， 于是，要使得 ST＞2008，只需 ＞2007。将 按照第一组 21 项，第 二组 22 项，……，第 组 项的方式分组，……6 分 由(2)可知，每一组的和不小于 1 2，且只有 ＝1 时等于 1 2，将这样的分组连续取 2×2007 组，加 上 a1，共有 24015 项，这 24015 项之和一定大于 1＋2007＝2008，故只需取 ＝24015,就能使得 ＞ 2008； …………8 分 (注：只要取出的 不小于 24015，并说出相应理由，都给满分) (4)设这样的 存在， ＝2 时，有 1＝ ⇒ ， ＝3 时，有 ＝ ⇒ ， 猜测 ＝ ( ≥2).下面用数学归纳法证明： ① ＝2,3 时，上面已证，猜测正确； ②设 ＝ ( ≥2)时， 即 成立 则 即 ＝ 时，猜测也正确。综上所述，存在 ＝ ，使得 对 于 大 于 1 的 正 整 数 都 成 立。 …………12 分 19．（１）由已知 , 得 平面 , 又 , ∴ 平面 , ∴ 为二面角 的平面角. ----------3 分 由已知 , 得 , n 122 −− nn SS n2 1 n 1S n 122 −− nn SS n 1 3 1 2 1 +⋅⋅⋅++ n 1 3 1 2 1 +⋅⋅⋅++ n n2 n T TS T )(nf n )12 11)(2( −+f 2)2( =f n 2 5 )13 1 2 11)(3( −++f 3)3( =f )(nf n n n n k k knf =)( )1(121 −=+⋅⋅⋅++ − kn SkSSS kkkn SSkSSSS +−=++⋅⋅⋅++ − )1(121 。)1)(1( )11 1)(1( )1( 1 −+= −+++= −+= +k k k Sk kSk kSk n )1( +k )(nf n )1)((121 −=+⋅⋅⋅++ − nn SnfSSS n ABPDADAB ⊥⊥ , ⊥AB PAD ABMN // ⊥MN PAD ,, DMMNPMMN ⊥⊥ PMD∠ DMNP −− 060=∠PAD 030=∠MPD ∵ 是 斜边 上的中线, ∴ 为等腰三角形, , 即二面角 的大小为 . -------------7 分 （２）显然 . 若 , 则 平面 , 而 平面 ，故平面 与平面 重合，与题意不符. 由 是 ，则必有 ， 连 BD，设 ，由已知得 ，从而 ， 又 ，∴ ，得 ， 故 平面 ， -----------9 分 ∴ ，又 ，∴ 平面 , ∴ ，反之亦然. ∵ ∴ , ∴ ∽ -------11 分 ∴ . --------12 分 20．解：（I） 的取值为 1， 3，又 ………………4 分 ∴ξ的分布列为 …………………………5 分 ∴Eξ=1× +3× = . ………………………………6 分 （II）当 S8=2 时，即前八秒出现“○”5 次和“×”3 次，又已知 若第一、三秒出现“○”，则其余六秒可任意出现“○”3 次； 若第一、二秒出现“○”，第三秒出现“×”，则后五秒可任出现“○”3 次. 故此时的概率为 …………12 分 21．解：（Ⅰ）设 的坐标为 ，则 且 ． 解得 ， 因此，点 的坐标为 ． （Ⅱ） ，根据椭圆定义， 得 ， ， ． ∴所求椭圆方程为 ． DM PDARt∆ PA MPMD = PMD∆ 0120=∠PMD DMNP −− 0120 090≠∠DCN 090=∠CDN ⊥CD PAN ⊥CD PAD PAN PAD CDN∆ ∆Rt DNCN ⊥ aAD = aAB 2= aBD 3= aADPD 360tan 0 == BDPD = PBDN ⊥ ⊥DN PBC BCDN ⊥ BCPD ⊥ ⊥BC PBD BCBD ⊥ CDAB // CDBABD ∠=∠ ABDRt∆ CDBRt∆ 2 3,, 2 22 ==== AB BD AB CD AB BDCDAB BD BD CD || 3S=ξ ,2 1== qp .4 1)3 1()2 1()3(,4 32)2 1()2 1()1( 3321 3 =⋅+===⋅⋅==∴ ξξ PCP 4 3 4 1 2 3 ),4,3,2,1(0 =≥ iSi ).2187 80(3 80 3 830)3 2()3 1()( 78 353 5 3 6 或=×=⋅⋅+= CCP 1F′ ),( nm 2 1 1 −=+m n 0322 12 =+−−⋅ nm 5 2,5 9 =−= nm 1F′ )5 2,5 9(− 11 PFFP =′ ||||||2 2121 FFPFFPa ′=+′= 22)05 2()15 9( 22 =−+−−= 2=∴ a 112 =−=b 12 2 2 =+ yx ξ 1 3 P 4 3 4 1 （Ⅲ） ， 椭圆的准线方程为 ． 设点 的坐标为 , 表示点 到 的距离， 表示点 到椭圆的右 准线的距离． 则 ， ． ， 令 ， 则 ， 当 ， ， ， ． ∴ 在 时取得最小值． 因此， 最小值＝ ，此时点 的坐标为 -----------------13 分 22．解：（Ⅰ）当 时，原不等式即 ，解得 ， ∴ 即 ------------------------------2 分 (Ⅱ)原不等式等价于 ……………………………………………..4 分 ………………………………………………………..6 分 ∴ ……8 分 （Ⅲ）∵ n=1 时， ；n=2 时， n=3 时， ；n=4 时， n=5 时， ；n=6 时， …………………………………………9 分 猜想： 时 下面用数学归纳法给出证明 ①当 n=5 时， ，已证…………………………………………………….10 分 2 2 = c a  ∴ 2±=x Q )32,( +tt )22( <<− t 1d Q 2F 2d Q 10105)32()1( 222 1 ++=++−= ttttd 22 −= td 2 22 2 1 )2( 2252 10105 − ++⋅=− ++= t tt t tt d d 2 2 )2( 22)( − ++= t tttf )22( <<− t 34 22 )2( )86( )2( )2(2)22()2()22()( − +−=− −⋅++−−⋅+=′ t t t ttttttf  0)(,3 42 <′−<<− tft 0)(,23 4 >′<<− tft 3 4−=t 0)( =′ tf )(tf 3 4−=t 2 1 d d 2 2)3 4(5 =−⋅ f Q )3 1,3 4(− 1k = 2 3 2 0x x− + ≤ 1 2x≤ ≤ x N+∈ 1,2x = (1) 2f = 1 1( 2 )( 2 ) 0 2 2k k k kx x x− −− − ≤ ⇔ ≤ ≤ ( ) 12122 11 +=+−= −− kkkkf 0 1 1 1 ( ) (1) (2) ( ) 2 2 2 2 1 n n n n i S f i f f f n n n− = = = + + + = + + + + = + −∑   22 nPS n nn −=− ;012 21 >− ;022 22 =− ;032 23 <− ;042 24 =− ;052 25 >− ;062 26 >− 5≥n nn PS > 55 PS > ②假设 时结论成立即 那么 n=k+1 时， 在 范围内， 恒成立,则 ，即 由①②可得，猜想正确，即 时， ………………………………….. 12 分 综上所述：当 n=2,4 时, ;当 n=3 时, ;当 n=1 或 时 ;---13 分 备选题：解：(1)∵ -------------------------------------------1 分 当 时， ，∴函数 在 上为增函数----------------3 分 ∴ ， --------------------------4 分 （２）证明：令 则 ∵当 时 ，∴函数 在区间 上为减函数 ∴ ，即在 上， ∴在区间 上，函数 的图象在函数 的图象的下方-----8 分 （3）证明：∵ ，当 时，不等式显然成立 当 时 ∵ ＝ -----① -------------②-----10 分 ①+②得 ≥ （当且仅当 时“＝”成立）---------------13 分 ∴当 时，不等式成立 ( )5≥= kkn 22, kPS k kk >> 1 2 2 2 22 ( 1) 2 2 2 1 2 2 1k kk k k k k k+ − + = ⋅ − − − > ⋅ − − − 2 22 1 ( 1) 2k k k= − − = − − 5≥k ( ) 021 2 >−−k 1 22 ( 1)k k+ > + 11 ++ > kK PS 5≥n nn PS > nn PS = nn PS < 5≥n nn PS > 1'( )f x x x = + [1, ]x e∈ '( ) 0f x > ( )f x [1, ]e 2 max 1( ) ( ) 2f x f e e= = min 1( ) (1) 2f x f= = − 2 31 2( ) ( ) ( ) ln 12 3F x f x g x x x x= − = + − − 2 3 2 21 1 2 (1 )(1 )'( ) 2 x x x x xF x x xx x x + − − + += + − = = 1x > '( ) 0F x < ( )F x (1, )+∞ 1 2( ) (1) 1 02 3F x F< = − − < (1, )+∞ ( ) ( )f x g x< (1, )+∞ ( )f x 32( ) 3g x x= 1'( )f x x x = + 1n = 2n ≥ 1 1[ '( )] '( ) ( ) ( )n n n n nf x f x x xx x − = + − + 1 2 2 3 1 2 1n n n n n n nC x C x C x − − − −+ + + [ '( )] '( )n nf x f x− = 1 2 1 2 2 3 1 1n n n n n nn nC C C xx x − − − − −+ + + 2 1 3 2 2 1 2 3 2 1 1 1 1[ '( )] '( ) [( ) ( ) ( ) ]2 n n n n n n n n nn n nf x f x x C x C x Cx x x − − − − − − −− = + + + + + + 1 2 1 2 2n n n n nC C C −+ + + = − 1x = 2n ≥ 综上所述得 ≥ .--------------------------14 分[ '( )] '( )n nf x f x− 2 2n − ( )n N ∗∈