2011高考物理试题分类汇编2 97页

1 2011普通高校招生考试试题汇编-电学实验 1(2011北京)（1）用如图1所示的多用电表测量电阻，要用到选择开关K和两个部件S、T。 请根据下列步骤完成电阻测量: ○1旋动部件________，使指针对准电流的"0"刻线。○2将K旋转到电阻挡"×l00"的位置。 ○3将插入"十"、"－"插孔的表笔短接，旋动部件_______，使指针对准电阻的_________ (填"0刻线"或"∞刻线")。 ○4将两表笔分别与侍测电阻相接，发现指针偏转角度过小。为了 得到比较准确的测量结果，请从下列选项中挑出合理的步骤， 并按_______的顺序避行操作，再完成读数测量。 A．将K旋转到电阻挡"×1k"的位置 B．将K旋转到电阻挡"×10"的位置 C．将两表笔的金属部分分别与被测电阻的两恨引线相接 D．将两表笔短接，旋动合适部件，对电表进行校准 1【答案】①S ③T 0 刻线 ④ADC 〖解析〗多用电表测量电阻时，在测量之前就要观察指针是否在零刻度线上，若指针不在零 刻度线上，用螺丝刀小心转动调零螺丝 S，使指针对准电流的“0”刻线.然后转动 选择开关 K，选择量程，再将两表笔短接，调整调零电阻的旋钮 T，使得指针对准满 偏刻度（即电阻的 0 刻线），接下来才能将两表笔的金属部分分别与被测电阻的两根 引线相接，测量被测电阻的阻值.若在测量过程中，发现指针偏转角度过小，表明被 测的电阻阻值很大，这时要换用更高倍率的挡位，例如，本题就要从“×100” 挡 位更换到“x1K”的位置. 2（2011 江苏）．(10 分) 某同学利用如图所示的实验电路来 测量电阻的阻值。 (1)将电阻箱接入 a、b之间，闭合开关。适当调节滑动变阻 器 R’后保持其阻值不变。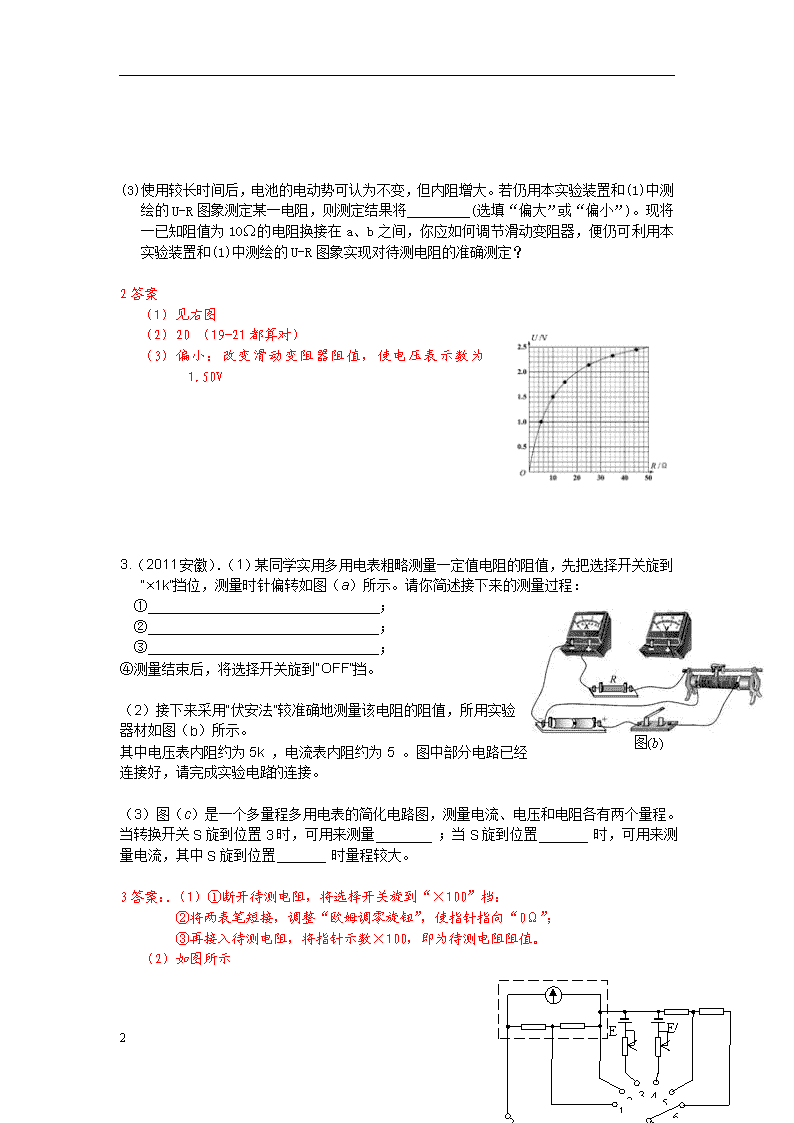改变电阻箱的阻值 R，得到一组 电压表的示数 U与 R的数据如下表： 请根据实验数据作出 U-R 关系图象。 (2)用待测电阻 RX替换电阻箱，读得电压表示数为 2.00V。 利用(1)中测绘的 U-R 图象可得 RX=_________ Ω。 2 (3)使用较长时间后，电池的电动势可认为不变，但内阻增大。若仍用本实验装置和(1)中测 绘的 U-R 图象测定某一电阻，则测定结果将_________(选填“偏大”或“偏小”)。现将 一已知阻值为 10Ω的电阻换接在 a、b 之间，你应如何调节滑动变阻器，便仍可利用本 实验装置和(1)中测绘的 U-R 图象实现对待测电阻的准确测定？ 2 答案 （1）见右图 （2）20 （19-21 都算对） （3）偏小：改变滑动变阻器阻值，使电压表示数为 1.50V 3.（2011安徽）．（1）某同学实用多用电表粗略测量一定值电阻的阻值，先把选择开关旋到 “×1k”挡位，测量时针偏转如图（a）所示。请你简述接下来的测量过程： ① ； ② ； ③ ； ④测量结束后，将选择开关旋到“OFF”挡。 （2）接下来采用“伏安法”较准确地测量该电阻的阻值，所用实验 器材如图（b）所示。 其中电压表内阻约为 5k ，电流表内阻约为 5 。图中部分电路已 经连接好，请完成实验电路的连接。 （3）图（c）是一个多量程多用电表的简化电路图，测量电流、电压和电阻各有两个量程。 当转换开关 S旋到位置 3时，可用来测量 ；当 S旋到位置 时，可用来测 量电流，其中 S旋到位置 时量程较大。 3 答案：．（1）①断开待测电阻，将选择开关旋到“×100”档： ②将两表笔短接，调整“欧姆调零旋钮”，使指针指向“0Ω”； ③再接入待测电阻，将指针示数×100，即为待测电阻阻值。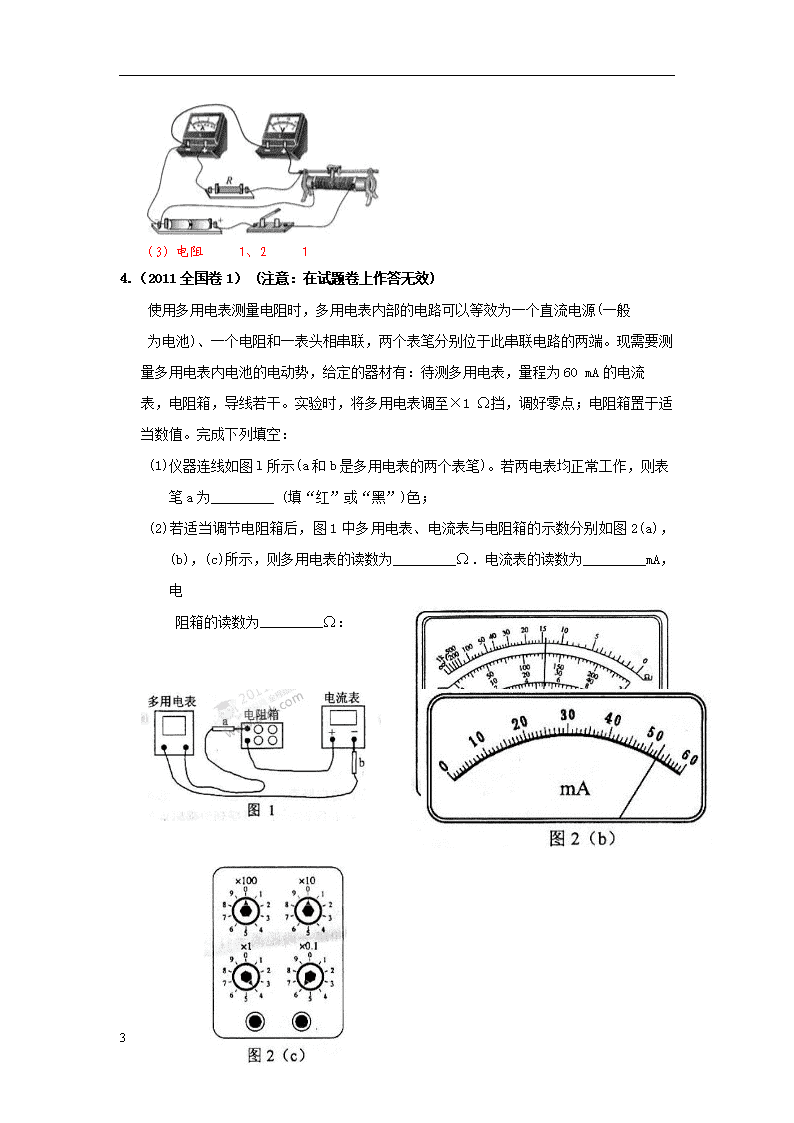 （2）如图所示 图(b) A B E E/ 红表笔 黑表笔 1 2 3 4 5 6 图(c) 3 （3）电阻 1、2 1 4.（2011 全国卷 1） (．注意：在试题卷上作答无效．．．．．．．．．．．．)． 使用多用电表测量电阻时，多用电表内部的电路可以等效为一个直流电源(一般 为电池)、一个电阻和一表头相串联，两个表笔分别位于此串联电路的两端。现需要测 量多用电表内电池的电动势，给定的器材有：待测多用电表，量程为 60 mA 的电流 表，电阻箱，导线若干。实验时，将多用电表调至×1 Ω挡，调好零点；电阻箱置于适 当数值。完成下列填空： (1)仪器连线如图 l 所示(a 和 b 是多用电表的两个表笔)。若两电表均正常工作，则表 笔 a 为_________ (填“红”或“黑”)色； (2)若适当调节电阻箱后，图 1中多用电表、电流表与电阻箱的示数分别如图 2(a)，(b)， (c)所示，则多用电表的读数为_________Ω．电流表的读数为_________mA，电 阻箱的读数为_________Ω： 4 (3)将图 l 中多用电表的两表笔短接，此时流过多用电表的电流为_________mA；(保留 3 位 有效数字) (4)计算得到多用电表内电池的电动势为_________V。(保留 3位有效数字) 4.解析：(1)黑(2)14.0、53.0、4.6 (3)102 (4)1.54 电表内阻 r=15Ω,外阻为 R=4.6Ω此时电流为：I=53mA,求出 E=I(R+r)=1.54V，从而求 出短路电流：I′= E r =102mA 5（2011 海南）.图 1是改装并校准电流表的电路图，已知表头 a的量程为 Ig=600 A 内阻为 Rg，A 是标准电流表，要求改装 后的电流表量程为 I=60mA。完成下列填空。 （1） 图 1 中分流电阻 Rp 的阻值为_______。 99 gR （2）在电表改装成后的某次校准测量中，a 表的示数如图所是，由此读出流过 a 电流表的 电流为___ 49.5mA。此时流过分流电阻 R 跑的电流为_______49.0mA（保留一位小数） 6（2011 全国理综）.（5 分） 为了测量一微安表头 A的内阻，某同学设计了如图所示的电路。图中 A0是标准电流表， R0和 RN分别是滑动变阻器和电阻箱，S 和 S1分别是单刀双掷开关和单刀开关，E 是电池。 完成下列实验步骤中的填空： 5 （1）将 S 拨向接点 1，接通 S1，调节________,使待测表头指针偏转到适当位置，记下此时 _____的读数 I； （2）然后将 S 拨向接点 2，调节________,使________,记下此时 RN的读数； （3）多次重复上述过程，计算 RN读数的________,此即为待测微安表头内阻的测量值。 6 解析：（1）R0、标准电流表 A0；（2）RN，标准电流表 A0的示数为 I；（3）平均值 7（2011天津）（4）某同学测量阻值约为 25kΩ的电阻 Rx，现备有下列器材： A．电流表（量程 100 μA，内阻约为 2 kΩ）； B．电流表（量程 500 μA，内阻约为 300 Ω）； C．电压表（量程 15 V，内阻约为 100 kΩ）； D．电流表（量程 50 V，内阻约为 500 kΩ）； E．直流电源（20 V，允许最大电流 1 A）； F．滑动变阻器（最大阻值 1 kΩ，额定功率 1 W）； G．电键和导线若干。 电流表应选 B ，电压表应选 C 。（填字母代号） 该同学正确选择仪器后连接了以下电路，为保证实验顺利进行，并使测量误差尽量减小， 实验前请你检查该电路，指出电路在接线上存在的问题： 1 电流表应采用内接的方法； 2 滑动变阻器应采用分压器方式的接法 。 7【解析】：电学实验选择仪器的一般步骤如下：① 根据量程选择电流表和电压表，不能超 过表的量程，不能量程太大导致表的读数偏小；② 根据题中关键语句，如精确测量， 从零开始连续可调等等选择分压电路亦或是限流电路；分压电路滑动变阻器选择小阻 值，限流电路滑动变阻器选择大阻值；③ 选择电流表的内外接法，一般的原则是“大 6 内偏大，小外偏小”；也可以根据 V x R R 与 x A R R 之间的关系来判断，当 V x R R > x A R R 时，采用电 流表的外接法，反之选择电流表内接法。 （1）本题中，待测电阻 Rx的阻值约为 25kΩ，直流电源电动势为 20V，经粗略计算电 路中最大的电流约为 max 3 20V 800μA 25 10 EI R      ，所以电流表选择 B；虽然电压表 C 的量程不足，但是相比起来电压表 D 的量程超过太多，读数偏小，所以电压表选择 C 表。 （2）根据本题解析的第②、③两条原则可知电路图的问题为：①电流表应采用内接的 方法；②滑动变阻器应采用分压器方式的接法 。 8（2011 浙江）.（10 分）在“探究导体电阻与其影响因素的定量关系”试验中，为了探究 3根材.料未知，横截面积均为 S=0.20mm 2 的金属丝 a、b、c的电阻率，采用如图所示的实验 电路，M 为金属丝 c的左端点，O 为金属丝 a 的右端点，P是金属丝上可移动的接触点。在 实验过程中，电流表读数始终 AI 25.1 。电压表读数U 随 OP 间距离 x 的变化如下表： （1）绘出电压表读数 U 随 OP 间距离 x变化的图线； （2）求出金属丝的电阻率  ，并进行比较。 8.答案：（1）如图所示； （2）电阻率的允许范围： a ： m 61096.0 ~ m 61010.1 b ： m 6105.8 ~ m 71010.1 c ： m 61096.0 ~ m 61010.1 通过计算可知，金属丝 a 与 c 电阻率相同，远大于金 属丝 b的电阻率。 解析：（1）以 OP 间距离 x 为横轴，以电压表读数 U 为纵轴，描点、连线绘出电压表读数 U 随 OP 间距离 x 变化的图线。 x/mm 600 700 800 900 1000 1200 1400 1600 1800 2000 2100 2200 2300 2400 U/V 3.9 5 4.5 0 5.1 0 5.9 0 6.50 6.65 6.82 6.93 7.02 7.15 7.85 8.50 9.05 9.75 7 （2）根据电阻定律 S lR  可得 l S I U l SR  。 mma        6 3 6 1004.1 10)6001000(25.1 1020.0)9.35.6( mmb        7 3 6 106.9 10)10002000(25.1 1020.0)5.61.7( mmc        6 3 6 1004.1 10)20002400(25.1 1020.0)1.77.9( 通过计算可知，金属丝 a与 c电阻率相同，远大于金属丝 b 的电阻率。 9（2011广东）（2）在“描绘小电珠的伏安特性曲线”实验中，所用器材有：小电珠（2.5V， 0.6W），滑动变阻器，多用电表，电流表，学生电源，开关，导线若干。 ①粗测小电珠的电阻，应选择多用电表_____倍率的电阻档（请填写“x1”、“x10”或“x100”）； 调零后，将表笔分别与小电珠的两极连接，示数如图 16，结果为_____  ②实验中使用多用电表测量电压，请根据实验原理图 17完成实物图 18中的连线。 ③开关闭合前，应将滑动变阻器的滑片 P置于____端。为使小电珠亮度增加，P应由中点 向_____端滑动。 ④下表为电压等间隔变化测得的数据，为了获得更准确的实验图象，必须在相邻数据点___ __间多测几组数据（请填写“ab” “bc” “cd” “de”或“ef”） 数据点 a b c d e F U/V 0.00 0.50 1.00 1.50 2.00 2.50 I/A 0.000 0.122 0.156 0.185 0.216 0.244 8 9 解析：答案：（2）x1 7.5 左端 右端 ab ①电珠电阻较小，故选“x1”档 ②如右图 ③P 置左端电珠两端电压最小 ④ab 之间电流值相差太大 10（2011上海）．(9 分)实际电流表有内阻，可等效为理想电流表与电阻的串联。测量实际 电流表 1G 内阻 1r 的电路如图所示。供选择的仪器如下： ①待测电流表 1G (0 ~ 5mA，内阻约300Ω)，②电流表 2G (0 ~10mA，内阻约100Ω)，③定 值电阻 1R (300Ω)，④定值电阻 2R (10Ω)，⑤滑动变阻器 3R (0 ~ 1000Ω)，⑥滑动变阻 器 4R (0 ~ 20Ω)，⑦干电池(1.5V)，⑧电键S及导线若干。 (1)定值电阻应选 ，滑动变阻器应选 。 (在空格内填写序号) (2)用连线连接实物图。 (3)补全实验步骤： ①按电路图连接电路， ； ②闭合电键S，移动滑动触头至某一位置，记录 1G ， 2G 的读数 1I ， 2I ； ③ ； ④以 2I 为纵坐标， 1I 为横坐标，作出相应图线，如图所示。 (4)根据 2 1I I 图线的斜率 k及定值电阻，写出待测电流表内阻的表达 式 。 10 答案. (1)③，⑥ (各 1分) (2)见图 (2分) (3)①将滑动触头移至最左端(写最小给分，最大不给分) ③多次移动滑动触头，记录相应的 1G ， 2G 读数 1 2,I I (1 分) 9 (4) 1 1( 1)r k R  (3 分) 11.（2011 山东） （2）某同学利用图甲所示电路，探究了电源在不同负载下的输出功率。 ①所得实验数据如下图，请在给出的直角坐标系上(见答题卡)画出U I 的图像。 ②根据所画U I 的图像，可求得电流 0.20I A 时电源的输出功率为________W 。 （保留两位有效数） ②实验完成后，该同学对实验方案进行了反思，认为按图甲电路进行实验操作的过程 中存在安全隐患，并对电路重新设计。在图乙所示的电路中，你认为既能测出电源在不同负 载下的输出功率，又能消除安全隐患的是 。（Rx阻值未知） 11 答案：①如图所示 ②0.37 ③b c 12（2011·重庆理综·T22（1））某电动机的三组线圈①、②、③阻值相同，均为几欧姆，接 法可能是题 22 图 1中甲、乙两种之一，A、B和 C是外接头。现有一组线圈断路，维 修人员通过多用电表测量外接头之间的电阻来判断故障，若测 A和 B之间、B和 C之 间、A和 C之间的电阻时，多用电表指针偏转分别如题 22图 2（a）、（b）、（c）所示， 10 则测量中使用的欧姆档的倍率是 （填 1 、 10 、 100 或 1k ），三组线圈 的接法是 （填甲或乙），断路线圈是 （填①、②或③）。 12【答案】⑴ 1 乙 〖解析〗测 A 和 B 之间、B 和 C 之间、A 和 C 之间的电阻时，多用电表指针都有偏转，一定 不是甲电路，因为甲电路中，只要有一个电阻断路，三次测量时，多用电表指针只可 能就一次有偏转。所以一定是乙电路.因为测量 A 和 B 之间、B和 C之间的电阻都是 4 Ω，而 B和 C之间的电阻是 8Ω，显然是线圈③发生了断路.题目中已经告诉线圈的 电阻是几个欧姆，结合多用表示数可以判断使用的挡位为“ 1 ” （2011·重庆理综·T22（2））（2）某同学设计了如题 22 图 3 所示的装置，利用米尺、秒表、 轻绳、轻滑轮、轨道、滑块、托盘和砝码等器材来制定滑块和轨道间的动摩擦因数μ。 滑块和托盘上分别放有若干砝码，滑块质量为 M，滑块上砝码总质量为 m ‘ ，托盘和盘中 砝码的总质量为 m，实验中，滑块在水平轨道上从 A 到 B 做初速为零的匀加速直线运动， 重力加速度 g 取 10m／s 2 。 11 2011普通高校招生考试试题汇编-力学实验 1（2011安徽）．为了测量某一弹簧的劲度系数，降该弹簧竖直悬挂起来，在自由端挂上 不同质量的砝码。实验册除了砝码的质量 m与弹簧长度 l的相应数据，七对应点已在图 上标出。（g=9.8m/s2) （1）作出 m-l的关系图线； （2）弹簧的劲度系数为 N/m. 解析：Ⅰ．（1）如图所示 （2）0.248~0.262 2（2011 江苏）．(8 分)某同学用如图所示的实验装置来验证“力的平行四边形定则”。弹簧 测力计 A 挂于固定点 P，下端用细线挂一重物 M。弹簧测力计 B 的一端用细线系于 O 点， 手持另一端向左拉，使结点 O 静止在某位置。分别读出弹簧测力计 A和 B 的示数，并在 贴于竖直木板的白 记录 O 点的位置和拉线的方向。 (1)本实验用的弹簧测力计示数的单位为 N，图中 A 的示数 为_______N。 (2)下列不必要．．．的实验要求是_________。(请填写选项前对 应的字母) (A)应测量重物 M 所受的重力 (B)弹簧测力计应在使用前校零 (C)拉线方向应与木板平面平行 (D)改变拉力，进行多次实验，每次都要使 O 点静止在同一位置 2 解析： 3(2011北京)如图2，用"碰撞实验器"可以验证动量守恒定律，即研究两个小球在轨道水平部 分碰撞前后的动量关系。 ○1实验中，直接测定小球碰撞前后的速度是不容易的。但 是，可以通过仅测量______ (填选项前的符号)，间接地 解决这个问题。 第一节 小球开始释放高度h 第二节 B．小球抛出点距地面的高度H C．小球做平抛运动的射程 12 ○2图2中O点是小球抛出点在地面上的垂直投影。实验时，先让入射球ml多次从斜轨上S 位置静止释放，找到其平均落地点的位置P，测量平抛射程OP。 然后，把被碰小球m2静置于轨道的水平部分，再将入射球ml从斜轨上S位置静止释放， 与小球m2相碰，并多次重复。接下来要完成的必要步骤是_________。(填选项前的符 号) A．用天平测量两个小球的质量ml、m2 B．测量小球m1开始释放高度h C．测量抛出点距地面的高度H D．分别找到m1、m2相碰后平均落地点的位置M、N E．测量平抛射程OM，ON ○3若两球相碰前后的动量守恒，其表达式可表示为_________ (用○2中测量的量表示)； 若碰撞是弹性碰撞，那么还应满足的表达式为___________ (用○2中测量的量表示)。 ○4经测定，m1=45.0g，m2=7.5g，小球落地点的平均位置距O点的距离如图3所示。碰 撞前、后m1的动量分别为p1与p1´，则p1:p1´=____ :11；若碰撞结束时m2的动量为p2´， 则p1´: p2´=11:_______。 实验结果表明，碰撞前、后总动量的比值 1 1 2 p p p  为____________。 ○5有同学认为，在上述实验中仅更换两个小球的材质，其它条件不变，可以使被碰小球 做平抛运动的射程增大。请你用○4中已知的数据，分析和计算出被碰小球m2平抛运动射 程ON的最大值为________cm。 3 答案 :①C，②ADE 或 DAE 或 DEA ③ OPmONmOMm  121 2 1 2 2 2 1 OPmONmOMm  ④14 2.9 1～1.01 ⑤76.8 〖解析〗①在落地高度不变的情况下，水平位移就能反映平抛初速度的大小，所以，仅测量 小球做平抛运动的射程就能间接测量速度.因此选 C. ②测量平均落点的位置，找到平抛的水平位移，因此步骤中 D、E 是必须的，而且要 D 先在 E 后，至于用天平测质量先后均可。所以答案是 ADE 或 DAE 或 DEA. ③设落地时间为 t，则 t OPv 1 ， t OMv 1 t ONv 2 ，动量守恒的表达式是 13 221111 vmvmvm  ， 动能守恒的表达式是 2 22 2 11 2 11 2 1 2 1 2 1 vmvmvm  ，所以若两球相碰前后的动量守恒，则 OPmONmOMm  121 成立，若碰撞是弹性碰撞，动能守恒则 2 1 2 2 2 1 OPmONmOMm  成立. ④碰撞前后 m1动量之比 11 14 20.35 80.44 1 1   OM OP p p ， 9.2 11 68.555.7 20.350.45 2 1 2 1       ONm OMm p p ， 01.1 68.555.720.3545 80.440.45 21 1 21 1        ONmOMm OPm pp p ⑤发生弹性碰撞时，被碰小球获得的速度最大，根据动量守恒和动能守恒， 221111 vmvmvm  ， 2 22 2 11 2 11 2 1 2 1 2 1 vmvmvm  ，联立解得 1 21 1 2 2 v mm m v   ，因此， 最大射程为 cmcm 80.7680.44 5.745 452    4(2011海南).现要通过实验验证机械能守恒定律。实验装置如图1所示： 水平桌面上固定一倾斜的气垫导轨；导轨上 A 点处有一带长方形遮光片 的滑块，其总质量为 M，左端由跨过轻质光滑定滑轮的细绳与一质量为 m 的砝码相连；遮光片两条长边与导轨垂直；导轨上 B 点有一光电门，可 以测试遮光片经过光电门时的挡光时间 t，用 d 表示 A 点到导轨低端 C 点的距离，h 表示 A 与 C 的高度差，b 表示遮光片的宽度，s 表示 A ,B 两点的距离，将遮光片通过光电门的平 均速度看作滑块通过 B 点时的瞬时速度。用 g 表示重力加速度。完成下列填空和作图； （1）若将滑块自 A 点由静止释放，则在滑块从 A运动至 B 的过程中，滑块、遮光片与砝码 组成的系统重力势能的减小量可表示为____ ( )h M m gs d  。动能的增加量可表示为 __ 2 2 1 ( ) 2 bm M t  。若在运动过程中机械能守恒， 2 1 t 与 s 的关系式为 2 1 t __ 2 2 1 2( ) ( ) hM dm g s t M m db    (2)多次改变光电门的位置，每次均令滑块自同一点（A 点）下滑，测量相应的 s 与 t 值， 结果如下表所示： 14 以 s 为横坐标， 2 1 t 为纵坐标，在答题卡上对应图 2 位置的坐标纸中描出第 1 和第 5 个数 据点；根据 5 个数据点作直线，求得该直线的斜率 k=________2.40___ 214 .10   sm (保 留 3位有效数字). 由测得的 h、d、b、M和 m数值可以计算出 2 1 s t  直线的斜率 ok ，将 k和 ok 进行比较，若 其差值在试验允许的范围内，则可认为此试验验证了机械能守恒定律。 5（2011 新课标） 利用图 1 所示的装置可测量滑块在斜面上运动的加速度。一斜面上安装有两个光电门， 其中光电门乙固定在斜面上靠近底端处，光电门甲的位置可移动， 当一带有遮光片的滑块自斜面上滑下时，与两个光电门都相连的计 时器可以显示出遮光片从光电门甲至乙所用的时间 t。改变光电门甲 的位置进行多次测量，每次都使滑块从同一点由静止开始下滑，并 用米尺测量甲、乙之间的距离 s，记下相应的 t值；所得数据如下表 所示。 完成下列填空和作图： 15 （1）若滑块所受摩擦力为一常量，滑块加速度的大小 a、滑块经过光电门乙时的瞬时速度 vt、测量值 s和 t四个物理量之间所满足的关系式是_______； (2)根据表中给出的数据，在图 2给出的坐标纸上画出 S t t  图线； （3）由所画出的 S t t  图线，得出滑块加速度的大小为 a=____________m/s2（保留 2 位 有效数字）。 5.答案：（1） s t =- 1 2 at+vt （2） S t t  图线如图所示。（3）2.0 解析：设滑块经过光电门甲的速度为 v0，由匀变速直线运动规律，s=(v0+vt)t/2， vt =v0+ at 联立解得 s t =- 1 2 at+vt。 S t t  图线的斜率等于 1 2 a，由 S t t  图线可知，其斜率等于 1.0，所 以滑块加速度的大小为 a=2.0 m/s2。 6(2011 浙江).（10 分）在“探究加速度与力、质量的关系”实验时，已提供了小车，一端 附有定滑轮的长木板、纸带、带小盘的细线、刻度尺、天平、导线。为了完成实验，还须从 下图中选取实验器材，其名称是 ① （漏选或全选得零分）；并分别写出所选器材的作用 ② 。 21.答案：①学生电源、电磁打点计时器、钩码、 砝码或电火花计时器、钩码、砝码 ②学生电源为电磁打点计时器提供交流电源；电磁 打点计时器（电火花计时器）记录小车运动的位置 和时间；钩码用以改变小车的质量；砝码用以改变 小车受到的拉力的大小，还可以用于测量小车的质 16 量。 解析：电磁打点计时器（电火花计时器）记录小车运动的位置和时间；钩码用以改变小车的 质量；砝码用以改变小车受到的拉力的大小，还可以用于测量小车的质量。如果选电磁打点 计时器，则需要学生电源，如果选电火花计时器，则不需要学生电源。 7（2011上海）.(5 分)如图，为测量作匀加速直线运动小车的加速度，将宽度均为b的挡光 片A、B固定在小车上，测得二者间距为d。 (1)当小车匀加速经过光电门时，测得两挡光片先后经过的时间 1t 和 2t ，则小车加速度 a  。 (2)(多选题)为减小实验误差，可采取的方法是( ) (A)增大两挡光片宽度b (B)减小两挡光片宽度b (C)增大两挡光片间距 d (D)减小两挡光片间 7 答案：． （1） 2 2 2 2 1 1 1[ ] 2 ( ) ( ) b d t t    (2)B，C 8（2011·重庆理综·）（2）某同学设计了如题 22 图 3所示的 装置，利用米尺、秒表、轻绳、轻滑轮、轨道、滑块、托盘和砝码等器材来制定滑块和轨道 间的动摩擦因数μ。滑块和托盘上分别放有若干砝码，滑块质量为 M，滑块上砝码总质量为 m‘，托盘和盘中砝码的总质量为 m，实验中，滑块在水平轨道上从 A到 B做初速为零的匀 加速直线运动，重力加速度 g取 10m／s2。 ①为测量滑块的加速度a，须测出它在 A、B间运动的 与 ，计算a的运动 学公式是 ； ②根据牛顿运动定律得到 a与m的关系为：     1 g a m g M m m        他想通过多次改变m，测出相应的a值，并利用上式来计算 。若要求a是m的一次函 数，必须使上式中的 保持不变，实验中应将从托盘中取出的砝码置 于 ； ③实验得到 a与m的关系如题 22图 4所示，由此可知μ= （取两位有效数字） 17 8；【答案】⑴①位移 时间 2 2 t Sa  ⑵ mm  滑块上 〖解析〗⑴将运动公式 2 2 1 atS  变形得 2 2 t Sa  ，测量出位移 S和发生位移 S的时间 t，求 得加速度 a ⑵以 m为研究对象， maTmg  ；以 mM  为研究对象， amMgmMT )()(   消去绳子的拉力 T，解得加速度 mmM gmMmga    )( ，化简可得     1 g a m g M m m        将加速度的表达式     1 g a m g M m m        与数学中的一次函数 bkxy  类比， “     1 g a m g M m m        ”就相当于图像的斜率 k，为了保证图像斜率不变，要求 mm  保持不 变，在实验中就要把从小车上拿下的砝码放置到托盘中，从托盘中拿下的砝码放置到小车上. “     1 g a m g M m m        ”相当于纵轴截距.在图像上取两个点（64×10 -3 ,0.23）、（67×10 -3 ,0.35），写出直 18 线的两点式方程 33 1067 35.0 1064 23.0       x y x y ，化简得 3.240  xy ，方程中的“ 3.23 ” 就是直线的纵轴截距，所以 3.2 g ，因为 2/10 smg  ，所以 23.0 9（2011广东卷）（1）图 14是“研究匀变数直线运动”实验中获得的一条纸带，O、A、B、 C、D和 E为纸带上六个计数点。加速度 大小用 a表示 ①OD间的距离为 cm ②图 15是根据实验数据绘出的 s—t2图线 （s为各计数点至同一起点的距离），斜率表示 ，其大小为 m/s2(保 留三位有效数字)。 9解析：（1）答案：1.20 a/2 0.933 1 要估读一位，②s=v0t+ 2 1 at2，斜率为 a/2 10（2011天津）．（18分） （1）某同学用测力计研究在竖直方向运行的电梯运动状态。他在地面上用测力计测量 砝码的重力，示数为 G。他在电梯中用测力计仍测量同一砝码的重力，发现测力计的示 数小于 G，由此判断此时电梯的运动状态可能是减速上升或加速下降。 【解析】：物体处于失重状态，加速度方向向下，故而可能是减速上升或加速下降。 （2）用螺旋测微器测量某金属丝直径的结果如图所示。 该金属丝的直径是 1.706mm 19 【解析】：注意副尺一定要有估读。读数为 1.5+20.6×0.01mm=1.706mm。因为个人情 况不同，估读不一定一致，本题读数 1.704-1.708都算正确。 （3）某同学用大头针、三角板、量角器等器材测半圆形玻璃砖的折射率。开始玻 璃 砖的位置如图中实线所示，使大头针 P1、P2与圆心 O在同一直线上，该直线 垂直于玻璃砖的直径边，然后使玻璃砖绕圆心 O缓慢转动，同时在玻璃砖直径 边一侧观察 P1、P2的像，且 P2的像挡住 P1的像。如此观察，当玻璃砖转到图 中虚线位置时，上述现象恰好消失。此时只需测量出玻璃砖直径边绕 O点转过 的角度，即可计算出玻璃砖的折射率。请用你的测量量表示出折射率 1 sin n   。 【解析】：由题意可知，当玻璃砖转过某一角度θ时，刚好发生全反 射，在直径边一侧观察不到 P1、P2的像，做出如图所示的光路图可 知，当转过角度θ时有 1 sin n   。 11（2011 湖北）．(6 分)(注意：在试题卷上作答无效) 在“油膜法估测油酸分子的大小”实验中，有下列实验步骤： ①往边长约为 40 cm 的浅盘里倒入约 2 cm 深的水．待水面稳定后将适量的痱子粉 均匀地撒在水面上。 ②用注射器将事先配好的油酸酒精溶液滴一滴在水面上，待薄膜形状稳定。 ③将画有油膜形状的玻璃板平放在坐标纸上，计算出油膜的面积，根据油酸的体 积和面积计算出油酸分子直径的大小。 ④用注射器将事先配好的油酸酒精溶液一滴一滴地滴入量筒中，记下量筒内每增 加一定体积时的滴数，由此计算出一滴油酸酒精溶液的体积。 ⑤将玻璃板放在浅盘上，然后将油膜的形状用彩笔描绘在玻璃板上。 完成下列填空： (1)上述步骤中，正确的顺序是__________。(填写步骤前面的数字) (2)将 1 cm3的油酸溶于酒精，制成 300 cm3的油酸酒精溶液；测得 l cm3的油酸 酒精溶液有 50 滴。现取一滴该油酸酒精溶液滴在水面上，测得所形成的油膜的面积 是 0.13 m2。由此估算出油酸分子的直径为_________m。(结果保留 l 位有效数字) 解析：(1) ④①②⑤③ (2)5×10 -10 m 6 10 1 11 10 50 300 5 10 0.13 vd m m s          θ θ P1 P2 O θ 20 12（2011四川）（7分）某研究性学习小组进行了如下实验： 如 图所示，在一端封闭的光滑细玻璃管中注满清水，水中 放一个红蜡做成的小圆柱体 R。将玻璃管的开口端用胶塞塞紧 后竖直倒置且与 Y轴重合，在 R从坐标原点以速度 v 0=3cm/s 匀速上浮的同时，玻璃管沿 x轴正方向做初速为零的匀加速直 线运动。同学们测出某时刻 R的坐标为（4，6）,此时 R 的速 度大小为 cm/s，R在上升过程中运动轨迹的示意图 是 。（R视为质点） 【解析】⑴“研究运动的合成与分解”实验中： 小圆柱体 R 在竖直方向匀速运动有 tvy 0 ， s scm cm v yt 2 /3 6 0  ，在水平方向做初速 为 0 的匀加速直线运动 2 2 1 atx  得 2/2 scma  ，R的速度大小为 scmtavv /5222 0  ，轨迹示意图是 D。 13（2011 山东）(1)某探究小组设计了“用一把尺子测定动摩擦因数”的实验方案。如图所 示，将一个小球和一个滑块用细绳连接，跨在斜面上端。开始时小球和滑块均静止，剪 短细绳后，小球自由下落，滑块沿斜面下滑，可先后听到小球落地和滑块撞击挡板的声 音，保持小球和滑块释放的位置不变，调整挡板位置，重复以上操作直到能同时听到小 球落地和滑块撞击挡板的声音。用刻度尺测出小球下落的 。 (2).高度 H、滑块释放点与挡板处的高度差 h 和沿斜面运动的位移 x。（空气阻力对本实验 的影响可以忽略） ①滑块沿斜面运动的加速度与重力加速度的比值为________。 ②滑块与斜面间的动摩擦因数为__________________。 ③以下能引起实验误差的是________。 a．滑块的质量 b．当地重力加速度的大小 c．长度测量时的读数误差 d．小球落地和滑块撞击挡板不同时 21 θ F 答案：① H x ② 22 2 1)( hxH xh   ③c d 2011 普通高校招生考试试题汇编-相互作用 1（2011 安徽）．一质量为 m 的物块恰好静止在倾角为 的斜面上。现对物块施加一个竖直 向下的恒力 F，如图所示。则物块 A．仍处于静止状态 B．沿斜面加速下滑 C．受到的摩擦力不便 D．受到的合外力增大 答案：A 解析：由于质量为 m 的物块恰好静止在倾角为 的斜面上，说明斜面对物块的作用力与物 块的重力平衡，斜面与物块的动摩擦因数μ=tan 。对物块施加一个竖直向下的恒力 F，使得 合力仍然为零，故物块仍处于静止状态，A 正确，B、D 错误。摩擦力由 mgsin 增大到 (F+mg)sin ，C 错误。 21．（18 分） Ⅰ．为了测量某一弹簧的劲度系数，降该弹簧竖直悬挂起来，在自由端挂上不同质量的砝 码。实验册除了砝码的质量 m与弹簧长度 l 的相应数据，七对应点已在图上标出。（g=9.8m/s2) （1）作出 m-l 的关系图线； （2）弹簧的劲度系数为 N/m. 解析：Ⅰ．（1）如图所示 （2）0.248~0.262 22 4（2011 海南）.如图，墙上有两个钉子 a 和 b，它们的连线与水平方向的夹角为 45°，两 者的高度差为 l。一条不可伸长的轻质细绳一端固定于 a 点，另一 端跨过光滑钉子 b 悬挂一质量为 m1 的重物。在绳子距 a 端 2 l 得 c 点有一固定绳圈。若绳圈上悬挂质量为 m2 的钩码，平衡后绳的 ac 段正好水平，则重物和钩码的质量比 1 2 m m 为 A. 5 B. 2 C. 5 2 D. 2 解析：平衡后设绳的 BC 段与水平方向成α角，则： 2tan 2,sin 5    对节点 C 分析三力平衡，在竖 直方向上有： 2 1 sinm g m g  得： 1 2 1 5 sin 2 m m    ，选 C 5（2011 海南）.如图，粗糙的水平地面上有一斜劈， 斜劈上一物块正在沿斜面以速度 v0匀速下滑，斜劈 保持静止，则地面对斜劈的摩擦力 A.等于零 B.不为零，方向向右 C.不为零，方向向左 D.不为零，v0较大时方向向左，v0较小时方向向右 解析：斜劈和物块都平衡对斜劈和物块整体受力分析知地面对斜劈的摩擦力为零，选 A 19（2011 山东）．如图所示，将两相同的木块 a、b 至于粗糙的水平地面上，中间用一轻弹 簧连接，两侧用细绳固定于墙壁。开始时 a、b 均静止。弹簧处于伸长状态，两细绳均有拉 23 力，a 所受摩擦力 0faF ，b 所受摩擦力 0fbF ，现将右侧细绳剪断，则剪断瞬间 （ ） A． faF 大小不变 B． faF 方向改变 C． fbF 仍然为零 D． fbF 方向向右 答案：AD 解析：对 b进行受力分析，剪断前 b受重力、支持力、向左弹簧的拉力和绳的拉 力由于它所受摩擦力 0fbF ，所以弹簧的拉力和绳的拉力是一对平衡力，当将 右侧细绳剪断瞬间，绳的拉力消失，但弹簧的拉力不变，所以 b受摩擦力 fbF 方 向向右，C错误，D正确；由于细绳剪断瞬间，弹簧的弹力不变，所以 faF 大小不 变，A正确，B错误。 1（2011 江苏）如图所示，石拱桥的正中央有一质量为 m 的对称楔形石块，侧面与竖直方 向的夹角为α,重力加速度为 g，若接触面间的摩擦力忽略不计，旵石块侧面所受弹力的大小 为 A． 2sin mg  B． 2 s mg co  C． 1 tan 2 mg  D． 1 t 2 mgco  答案：A 9(2011 江苏)．如图所示，倾角为α的等腰三角形斜面固定在水平面上，一足够长的轻质绸 带跨过斜面的顶端铺放在斜面的两侧，绸带与斜面间无摩擦。现将质量分别为 M、m(M>m)的 小物块同时轻放在斜面两侧的绸带上。两物块与绸带间的动摩擦因数相等，且最大静摩擦力 与滑动摩擦力大小相等。在α角取不同值的情况下，下列说法正确的有 A．两物块所受摩擦力的大小总是相等 B．两物块不可能同时相对绸带静止 C．M不可能相对绸带发生滑动 D．m不可能相对斜面向上滑动 答案：AC 2011 普通高校招生考试试题汇编-选修 3-3 1（2011 全国卷 1 第 14 题）.关于一定量的气体，下列叙述正确的是 A.气体吸收的热量可以完全转化为功 B.气体体积增大时，其内能一定减少 C．气体从外界吸收热量，其内能一定增加 D．外界对气体做功，气体内能可能减少 24 解析： A 违背热力学第二定律，BCD 考察热力学第一定律：Q w U   做功和热传递 都可以改变内能故选 D 2（2011 全国卷 1 第 22 题）．(6 分) 在“油膜法估测油酸分子的大小”实验中，有下列实验步骤： ①往边长约为 40 cm 的浅盘里倒入约 2 cm 深的水．待水面稳定后将适量的痱子粉 均匀地撒在水面上。 ②用注射器将事先配好的油酸酒精溶液滴一滴在水面上，待薄膜形状稳定。 ③将画有油膜形状的玻璃板平放在坐标纸上，计算出油膜的面积，根据油酸的体 积和面积计算出油酸分子直径的大小。 ④用注射器将事先配好的油酸酒精溶液一滴一滴地滴入量筒中，记下量筒内每增 加一定体积时的滴数，由此计算出一滴油酸酒精溶液的体积。 ⑤将玻璃板放在浅盘上，然后将油膜的形状用彩笔描绘在玻璃板上。 完成下列填空： (1)上述步骤中，正确的顺序是__________。(填写步骤前面的数字) (2)将 1 cm3的油酸溶于酒精，制成 300 cm3的油酸酒精溶液；测得 l cm3的油酸 酒精溶液有 50 滴。现取一滴该油酸酒精溶液滴在水面上，测得所形成的油膜的面积是 0.13 m2。由此估算出油酸分子的直径为_________m。(结果保留 l位有效数字) 解析：(1) ④①②⑤③ (2)5×10 -10 m 6 10 1 11 10 50 300 5 10 0.13 vd m m s          3（2011 海南第 17 题模块 3-3 试题）（12 分） （1）（4 分）关于空气湿度，下列说法正确的是 （填入正确选项前的字母。选 对 1 个给 2分，选对 2 个给 4分；选错 1 个扣 2分，最低得 0分）。 A．当人们感到潮湿时，空气的绝对湿度一定较大 B．当人们感到干燥时，空气的相对湿度一定较小 C．空气的绝对湿度用空气中所含水蒸汽的压强表示 D．空气的相对湿度定义为水的饱和蒸汽压与相同温度时空气中所含水蒸气的压强之比 （2）（8 分）如图，容积为 1V 的容器内充有压缩空气。容器与水银压强计相连，压强计左右 两管下部由软胶管相连。气阀关闭时，两管 中水银面登高，左管中水银面上方到气阀之 25 间空气的体积为 2V 。打开气阀，左管中水银下降；缓慢地向上提右管，使左管中水银面回 到原来高度，此时右管与左管中水银面的高度差为 h。已知水银的密度为  ，大气压强为 OP ， 重力加速度为 g；空气可视为理想气体，其温度不变。求气阀打开前容器中压缩空气的压强 P1。 解析：由玻马定律得 1 1 0 2 0 1 2( )( )p v p v p gh v v    求出： 1 2 0 1 1 1 ( )gh v v p vp v     4（2011 全国理综第 33 题）.【选修 3-3】（15 分） （1）（6 分）对于一定量的理想气体，下列说法正确的是______。（选对一个给 3 分， 选对两个给 4 分，选对 3个给 6 分。每选错一个扣 3分，最低得分为 0分）（ADE） A 若气体的压强和体积都不变，其内能也一定不变 B 若气体的内能不变，其状态也一定不变 C 若气体的温度随时间不段升高，其压强也一定不断增大 D 气体温度每升高 1K 所吸收的热量与气体经历的过程有关 E当气体温度升高时，气体的内能一定增大 解析：理想气体的内能只由温度决定，由理想气体状态方程 C T PV  可知，若气体的 压强和体积都不变，温度 T 也不变，所以内能也一定不变，A、E 选项正确。若气体的内能 不变，则温度 T 不变，但气体的压强和体积可以改变，B项错误。若气体的温度升高，体积 增大，其压强可以不变， C 项错误。由热力学第一定律 WQU  知，D选项正确。 （2）（9分）如图，一上端开口，下端封闭的细长玻璃管，下部有长 l1=66cm 的水银柱， 中间封有长 l2=6.6cm 的空气柱，上部有长 l3=44cm 的水银柱，此时水银面恰好与管口平齐。 已知大气压强为 Po=76cmHg。如果使玻璃管绕低端在竖直平面内缓慢地转动一周，求在开口 向下和转回到原来位置时管中空气柱的长度。封入的气体可视为理想气体，在转动过程中没 有发生漏气。 解析：设玻璃管开口向上时，空气柱压强为 301 glPP  ① 式中， g和 分 别表示水银的密度和重力加速度。 玻璃管开口响下时，原来上部的水银有一部分会流出，封闭端会有部分真空。设此时开 口端剩下的水银柱长度为 x，则 12 glP  ， 02 PgxP   ② 式中， 2P 管内空气柱 的压强。由玻意耳定律得 )()( 221 shPslP  ③ 式中,h 是此时空气柱的长度，S 为玻璃 管的横截面积。 由①②③式和题给条件得 h=12cm ④ 从开始转动一周后，设空气柱的压强为 3P ，则 gxPP  03 ⑤ 由玻意耳定律得 )()( 321 hsPslP  ⑥ 式中， h是此时空气柱的长度。 由①②③⑤⑥ h 9.2cm ⑦ 26 5（2011 广东第 13 题）.如图 3所示,两个接触面平滑的铅柱压紧后悬挂 起来,下面的铅柱不脱落,主要原因是 A.铅分子做无规则热运动 B.铅柱受到大气压力作用 C.铅柱间存在万有引力作用 D.铅柱间存在分子引力 作用 解析：考查分子力、大气压力、万有引力之间的区别。选 D 6（2011 广东第 14 题）.图 4为某种椅子与其升降部分的结构示意图,M、N 两筒间密闭了一 定质量的气体，M可沿 N 的内壁上下滑动，设筒内气体不与外界发生热交换，在 M 向下滑动 的过程中 A.外界对气体做功，气体内能增大 B.外界对气体做功，气体内能减小 C.气体对外界做功，气体内能增大 D.气体对外界做功，气体内能减小 解析：由热力学第二定律△U=Q+W，Q=0，W>0，△U>0.选 A 7 (2011上海第4题)．如图，一定量的理想气体从状态a沿直线变化到状态b，在此过程中， 其压强 (A)逐渐增大 (B)逐渐减小 (C)始终不变 (D)先增大后减小 答案：A 8 (2011上海第8题)．某种气体在不同温度下的气体分 子速率分布曲线如图所示，图中 ( )f v 表示 v处单位速 率区间内的分子数百分率，所对应的温度分别为 , ,I II IIIT T T ，则 (A) I II IIIT T T  (B) III III IT T T  (C) ,II I II IIIT T T T  (D) I II IIIT T T  答案：B 9（2011上海第27题）.(5 分)在“用单分子油膜估测分子大小”实验中， (1)某同学操作步骤如下： ①取一定量的无水酒精和油酸，制成一定浓度的油酸酒精溶液； ②在量筒中滴入一滴该溶液，测出它的体积； ③在蒸发皿内盛一定量的水，再滴入一滴油酸酒精溶液，待其散开稳定； ④在蒸发皿上覆盖透明玻璃，描出油膜形状，用透明方格纸测量油膜的面积。 改正其中的错误： 27 (2)若油酸酒精溶液体积浓度为0.10% ，一滴溶液的体积为 34.8 10 ml ，其形成的油膜面 积为 240cm ，则估测出油酸分子的直径为 m。 答案 (1) ②在量筒中滴入 N 滴溶液 (1 分) ③在水面上先撒上痱子粉 (1 分) (2) 91.2 10 (3 分) 10（2011上海第30题）.(10 分)如图，绝热气缸A与导热气缸B均固定于地面，由刚性杆连接 的绝热活塞与两气缸间均无摩擦。两气缸内装有处于平衡状态的理想气体，开始时体积均为 0V 、温度均为 0T 。缓慢加热A中气体，停止加热达到稳 定后，A中气体压强为原来的1.2倍。设环境温度始终保 持不变，求气缸A中气体的体积 AV 和温度 AT 。 答案.(10 分) 设初态压强为 0p ，膨胀后 A，B 压强相等 01.2Bp p (1 分) B 中气体始末状态温度相等 0 0 0 01.2 (2 )Ap V p V V  (3 分) ∴ 0 7 6AV V (1 分) A 部分气体满足 0 0 0 0 0 1.2 A p V p V T T  （4 分） ∴ 01.4AT T （1分） 11（2011 山东第 36 题 3-3］） 人类对自然的认识是从宏观到微观不断深入的过程，以下说法正确的是 。 a．液晶的分子势能与体积有关 b．晶体的物理性质都是各向异性的 c．温度升高，每个分子的动能都增大 d．露珠呈球状是由于液体表面张力的作用 28 （2）气体温度计结构如图所示。玻璃测温泡 A 内充有理想气体，通过细玻璃管 B 和水银压 强计相连。开始时 A 处于冰水混合物中，左管 C 中水银面在 O点处，右管 D 中水银面高出 O 点 1h =44cm。（已知外界大气压为 1 个标准大气压，1 标准大气压相当于 76cmHg） （1）求恒温槽的温度 （2）此过程 A内气体内能 （填“增大”或“减小”）， 气体不对外做功，气体将 (填“吸热”或者“放热”) 解析：(1)答案：AD（2）91°C ；增大，吸热 12(2011 江苏 12A（选修模块 3－3）)．（12 分） (1)如题 12A-1 图所示，一淙用的“永动机”转轮由 5根轻杆和 转轴构成，轻杆的末端装有形状记忆合金制成的叶片，轻推转 轮后，进入热水的叶片因伸展面“划水”，推动转轮转动。离开 热水后，叶片形状迅速恢复，转轮因此能较长时间转动。下列 说法正确的是 A．转轮依靠自身惯性转动，不需要消耗外界能量 B．转轮转动所需能量来自形状记忆合金自身 C．转动的叶片不断搅动热水，水温升高 D．叶片在热水中吸收的热量一定大于在空气中释放的热量 (2)如题 12A-2 图所示，内壁光滑的气缸水平放置。一定质量的理想气体被密封在气缸内， 外界大气压强为 P0。现对气缸缓慢加热，气体吸收热量 Q 后，体积由 V1增大为 V2。则在此 过程中，气体分子平均动能_________(选增“增大”、“不变”或“减小”)，气体内能变化 了_____________。 (3)某同学在进行“用油膜法估测分子的大小”的实验前，查阅数据手册得知：油酸的摩尔 质量 M=0.283kg·mol -1 ，密度ρ=0.895×10 3 kg·m -3 .若 100 滴油酸的体积为 1ml，则 1 滴油 酸所能形成的单分子油膜的面积约是多少？(取NA=6.02×10 23 mol -1 .球的体积V与直径D的关 系为 31 6 V D ，结果保留一位有效数字) 答案 ： 29 13(重庆第 15 题).某汽车后备箱内安装有撑起箱盖的装置，它主要由气缸和活塞组成.开箱 时，密闭于气缸内的压缩气体膨胀，将箱盖顶起，如题 15 图所示.在此过程中，若缸内气体 与外界无热交换，忽略气体分子间相互作用，则缸内气体 A.对外做正功，分子的平均动能减小 B. 对外做正功，内能增大 C. 对外做负功，分子的平均动能增大 D. 对外做负功，内能减小 2011 普通高校招生考试试题汇编-磁场 1（2011 全国卷 1第 15 题）。如图，两根相互平行的长直导线分别通有方向相反的电流 1I 和 2I ，且 1 2I I ；a、b、c、d 为导线某一横截面所在平面内的四点，且 a、b、c与两导线共 面；b点在两导线之间，b、d的连线与导线所在平面垂直。磁感应强度可能为零的点是 A.a 点 B.b 点 C.c 点 D.d 点 解析：要合磁感应强度为零，必有 1I 和 2I 形成两个场等 大方向，只有 C点有可能，选 C 2（2011 海南第 7 题）．自然界的电、热和磁等现象都是相互联系的，很多物理学家为寻找 它们之间的联系做出了贡献。下列说法正确的是 A.奥斯特发现了电流的磁效应，揭示了电现象和磁现象之间的联系 × · I1 I2 · · · · a b c d 30 B.欧姆发现了欧姆定律，说明了热现象和电现象之间存在联系 C.法拉第发现了电磁感应现象，揭示了磁现象和电现象之间的联系 D.焦耳发现了电流的热效应，定量得出了电能和热能之间的转换关系 解析：考察科学史，选 ACD 3（2011 海南第 10 题）.空间存在方向垂直于纸面向里的匀强磁场，图中的正方形为其边界。 一细束由两种粒子组成的粒子流沿垂直于磁场的方向从 O 点入射。这两种粒子带同种电荷， 它们的电荷量、质量均不同，但其比荷相同，且都包含不同速率的粒子。不计重力。下列说 法正确的是 A.入射速度不同的粒子在磁场中的运动时间一定不同 B. 入射速度相同的粒子在磁场中的运动轨迹一定相同 C.在磁场中运动时间相同的粒子，其运动轨迹一定相同 D.在磁场中运动时间越长的粒子，其轨迹所对的圆心角一定越大 解析：在磁场中半径 mvr qB  运动时间： mt qB   （θ为转过圆心 角），故 BD 正确，当粒子从 O 点所在的边上射出的粒子时：轨迹可以不同，但圆心角相同为 1800，因而 AC 错 4（2011 新课标理综第 14 题）.为了解释地球的磁性，19 世纪安培假设：地球的磁场是由绕 过地心的轴的环形电流 I引起的。在下列四个图中，正确表示安培假设中环形电流方向的是 （B） 解析：主要考查安培定则和地磁场分布。根据地磁场分布和安培定则判断可知正确答案是 B。 5．（2011 新课标理综第 18 题）.电磁轨道炮工作原理如图所示。待发射弹体可在两平行轨 道之间自由移动，并与轨道保持良好接触。电流 I 从一条轨道流入，通过导电弹体后从另一 条轨道流回。轨道电流可形成在弹体处垂直于轨道面得磁场（可视为匀强磁场），磁感应强 度的大小与 I 成正比。通电的弹体在轨道上受到 安培力的作用而高速射出。现欲使弹体的出射速 度增加至原来的 2 倍，理论上可采用的方法是 （BD） A.只将轨道长度 L 变为原来的 2 倍 B.只将电流 I 增加至原来的 2倍 C.只将弹体质量减至原来的一半 31 D.将弹体质量减至原来的一半，轨道长度 L变为原来的 2倍，其它量不变 解析：主要考查动能定理。利用动能定理有 2 2 1 mvBIlL  ,B=kI 解得 m lLkIv 22  。所以 正确答案是 BD。 6（2011 浙江第 20 题）.利用如图所示装置可以选择一定速度范围内的带电粒子。图中板 MN 上方是磁感应强度大小为 B、方向垂直纸面向里的匀强磁场，板上有两条宽度分别为 2d 和 d 的缝，两缝近端相距为 L。一群质量为 m、电荷量 为 q，具有不同速度的粒子从宽度为 2d 的缝垂直 于板 MN 进入磁场，对于能够从宽度为 d的缝射出 的粒子，下列说法正确的是 A. 粒子带正电 B. 射出粒子的最大速度为 m dLqB 2 )3(  C. 保持 d 和 L 不变，增大 B，射出粒子的最大速度与最小速度之差增大 D. 保持 d 和 B 不变，增大 L，射出粒子的最大速度与最小速度之差增大 答案：BC 解析：由左手定则可判断粒子带负电，故 A 错误；由题意知：粒子的最大半径 2 3 max dLr   、 粒子的最小半径 2min Lr  ，根据 qB mvr  ，可得 m dLqBv 2 )3( max   、 m qBLv 2min  ，则 m qBdvv 2 3 minmax  ，故可知 B、C 正确，D错误。 7(2011上海第18题)． 如图，质量为m、长为 L的直导线用两绝缘细线悬挂于 'O O、 ，并处于匀强磁场中。当导 线中通以沿 x正方向的电流 I ，且导线保持静止时，悬线与竖直方向夹角为 。则磁感应强 度方向和大小可能为 (A) z正向， tanmg IL  (B) y正向， mg IL (C) z负向， tanmg IL  (D)沿悬线向上， sinmg IL  答案：BC 8（2011 安徽第 23）．（16 分） 如图所示，在以坐标原点 O 为圆心、半径为 R 的半圆 x y O P B 32 形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为 B，磁场方向垂直于 xOy 平面 向里。一带正电的粒子（不计重力）从 O 点沿 y 轴正方向以某一速度射入，带电粒子恰好做 匀速直线运动，经 t0时间从 P 点射出。 （1）求电场强度的大小和方向。 （2）若仅撤去磁场，带电粒子仍从 O 点以相同的速度射入，经 0 2 t 时间恰从半圆形区域的边 界射出。求粒子运动加速度的大小。 （3）若仅撤去电场，带电粒子仍从 O 点射入，且速度为原来的 4倍，求粒子在磁场中运动 的时间。 解析：（1）设带电粒子的质量为 m，电荷量为 q，初速度为 v，电场强度为 E。可判断出粒子 受到的洛伦磁力沿 x轴负方向，于是可知电场强度沿 x 轴正方向 且有 qE=qvB ① 又 R=vt0 ② 则 0 BRE t  ③ （2）仅有电场时，带电粒子在匀强电场中作类平抛运动 在 y 方向位移 2 2 ty v ④ 由②④式得 2 Ry  ⑤ 设在水平方向位移为 x，因射出位置在半圆形区域边界上，于是 3 2 x R 又有 201 ( ) 2 2 tx a ⑥ 得 2 0 4 3Ra t  ⑦ （3）仅有磁场时，入射速度 4v v  ，带电粒子在匀强磁场中作匀速圆周运动，设轨道半径 为 r，由牛顿第二定律有 2vqv B m r    ⑧ 又 qE=ma ⑨ 由⑦⑧⑨式得 3 3 Rr  ⑩ 由几何关系 sin 2 R r   ○11 即 3sin 2   3   ○12 33 带电粒子在磁场中运动周期 2 mT qB   则带电粒子在磁场中运动时间 2 2Rt T   所以 0 3 18Rt t ○13 9（2011 全国卷 1 第 25）.（19 分） 如图，与水平面成 45°角的平面 MN 将空间分成 I 和 II 两个区域。一质量为 m、电荷量为 q （q＞0）的粒子以速度 0v 从平面 MN 上的 0p 点水平右射入 I 区。粒子在 I区运动时，只受到大小不变、方向竖直向下的 电场作用，电场强度大小为 E；在 II 区运动时，只受到匀强 磁场的作用，磁感应强度大小为 B，方向垂直于纸面向里。 求粒子首次从 II 区离开时到出发点 0p 的距离。粒子的重力 可以忽略。 解析：设粒子第一次过 MN 时速度方向与水平方向成α1角， 位移与水平方向成α2角且α2=45 0 ，在电场中做类平抛运动， 则有： 0 2 , 1 , 2 v t x x y Eqat y a m     得出： 1 0 tan 2at v    0 02 , 5yv v v v  在电场中运行的位移: 2 2 2 2 0 0 1 2 2 2 2v mvs x y a Eq     在磁场中做圆周运动，且弦切角为α=α1-α2， 1 2 1 2 tan tan 1 10tan ,sin 1 tan tan 3 10            2vqvB m R  得出： 05mvR qB  在磁场中运行的位移为： 0 2 22 sin mvs R qB   所以首次从 II 区离开时到出发点 0p 的距离为： 2 0 0 1 2 2 2 2mv mvs s s qE qB     10（2011 新课标理综第 25 题）.（19 分） 如图，在区域 I（0≤x≤d）和区域 II（d≤x≤2d）内分别存在匀强磁场，磁感应强度大小 分别为 B 和 2B，方向相反，且都垂直于 Oxy 平面。一质量为 m、带电荷量 q（q＞0）的粒子 34 a 于某时刻从 y 轴上的 P点射入区域 I，其速度方向沿 x 轴正向。已知 a 在离开区域 I 时， 速度方向与 x轴正方向的夹角为 30°；因此，另一质量和电荷量均与 a相同的粒子 b 也从 p 点沿 x 轴正向射入区域 I，其速度大小是 a 的 1/3。不计重力和两粒子之间的相互作用力。 求 （1）粒子 a 射入区域 I 时速度的大小； （2）当 a 离开区域 II 时，a、b 两粒子的 y坐标之差。 解析：（1）设粒子 a 在 I 内做匀速圆周运动的圆心为 C（在 y 轴上），半径为 Ra1，粒子速率 为 va，运动轨迹与两磁场区域边界的交点为 P ,如图，由洛仑兹力公式和牛顿第二定律得 1 2 a a R vmABqv  ① 由几何关系得  PPC ② sin1 dRa  ③ 式中， 030 ，由①②③式得 m qBdva 2 1  ④ (2)设粒子 a 在 II 内做圆周运动的圆心为 Oa,半径为 1aR ，射出点为 aP （图中未画出轨迹），   aaPOP 。由洛仑兹力公式和牛顿第二定律得 2 2 )2( a a a R v mBqv  ⑤ 由①⑤式得 2 1 2 a a R R  ⑥ C、 P和 aO 三点共线，且由 ⑥式知 aO 点必位于 dx 2 3  ⑦ 的平面上。由对称性知， aP 点与 P点纵坐标相同，即 hRy apa  cos1 ⑧ 式中，h 是 C 点的 y坐标。 设 b 在 I 中运动的 轨道半径为 1bR ，由洛仑 兹力公式和牛 顿第二定律得 2 1 ) 3 () 3 ( a b a v R mB v q  ⑨ 设 a 到达 aP 点时，b位于 bP 点，转过的角度为 。如果 b 没有飞出 I，则 O B x · · · y d 2d 2B P Ⅰ Ⅱ 35   22   aT t ⑩   21  bT t ○11 式中，t 是 a 在区域 II 中运动的时间，而 v R T a a 2 2 2  ○12 3 2 1 1 v R T b b   ○13 由⑤⑨⑩○11○12○13式得 030 ○14 由①③⑨○14式可见，b 没有飞出。 bP 点的 y坐标为 hRy bpb  )cos2(1  ○15 由①③⑧⑨○14○15式及题给条件得，a、b两粒子的 y 坐标之差为 dyy ba pp )23( 3 2  ○16 11（2011 天津第 12 题）．（20 分）回旋加速器在核科学、核技术、核医学等高新技术领域得 到了广泛应用，有力地推动了现代科学技术的发展。 （1）当今医学成像诊断设备 PET/CT 堪称“现代医学高科技之冠”，它在医疗诊断中，常利 用能放射电子的同位素碳 11 为示踪原子，碳 11 是由小型回旋加速器输出的高速质子轰击氮 14 获得，同时还产生另一粒子，试写出核反应方程。若碳 11 的半衰期τ为 20min，经 2.0h 剩余碳 11 的质量占原来的百分之几？（结果取 2 位有效数字） （2）回旋加速器的原理如图，D1和 D2是两个中空的半 径为 R的半圆金属盒，它们接在电压一定、频率为 f的 交流电源上，位于 D1圆心处的质子源 A能不断产生质子 （初速度可以忽略，重力不计），它们在两盒之间被电 场加速，D1、D2置于与盒面垂直的磁感应强度为 B 的匀 强磁场中。若质子束从回旋加速器输出时的平均功率为 P，求输出时质子束的等效电流 I 与 P、B、R、f 的关系 式（忽略质子在电场中运动的时间，其最大速度远小于光速） （3）试推理说明：质子在回旋加速器中运动时，随轨道半径 r 的增大，同一盒中相邻轨道 的半径之差 r 是增大、减小还是不变？ 解析：（1）核反应方程为 14 1 11 4 7 1 6 2N H C+ He → ① 设碳 11 原有质量为 m0，经过 t=2.0h 剩余的质量为 mt，根据半衰期定义，有： 120 20 0 1 1 1.6% 2 2 t tm m              ② 36 （2）设质子质量为 m，电荷量为 q，质子离开加速器时速度大小为 v，由牛顿第二定律知： 2vqvB m R  ③ 质子运动的回旋周期为： 2 2R mT v qB     ④ 由回旋加速器工作原理可知，交变电源的频率与质子回旋频率相同，由周期 T与频率 f的关 系可得： 1f T  ⑤ 设在 t时间内离开加速器的质子数为 N，则质子束从回旋加速器输出时的平均功率 21 2 N mv P t   ⑥ 输出时质子束的等效电流为： NqI t  ⑦ 由上述各式得 2 PI BR f  若以单个质子为研究对象解答过程正确的同样给分 （3）方法一： 设 k（k∈N*）为同一盒子中质子运动轨道半径的序数，相邻的轨道半径分别为 rk，rk+1（rk>rk+1）， 1k k kr r r   ，在相应轨道上质子对应的速度大小分别为 vk，vk+1，D1、D2之间的电压为 U， 由动能定理知 2 2 1 1 12 2 2k kqU mv mv  ⑧ 由洛伦兹力充当质子做圆周运动的向心力，知 k k mvr qB  ，则 2 2 2 2 12 ( ) 2 k k q BqU r r m   ⑨ 整理得 2 1 4 ( )k k k mUr qB r r    ⑩ 因 U、q、m、B 均为定值，令 2 4mUC qB  ，由上式得 1 k k k Cr r r     ⑾ 相邻轨道半径 rk+1，rk+2之差 1 2 1k k kr r r     同理 1 2 k k k Cr r r     37 因为 rk+2> rk，比较 kr ， 1kr  得 1k kr r   说明随轨道半径 r 的增大，同一盒中相邻轨道的半径之差 r 减小 方法二： 设 k（k∈N*）为同一盒子中质子运动轨道半径的序数，相邻的轨道半径分别为 rk，rk+1（rk>rk+1）， 1k k kr r r   ，在相应轨道上质子对应的速度大小分别为 vk，vk+1，D1、D2之间的电压为 U 由洛伦兹力充当质子做圆周运动的向心力，知 k k mvr qB  ，故 1 1 k k k k r v r v   ⑿ 由动能定理知，质子每加速一次，其动能增量 kE qU  ⒀ 以质子在 D2盒中运动为例，第 k 次进入 D2时，被电场加速（2k﹣1）次 速度大小为 (2 1)2 k k qUv m   ⒁ 同理，质子第（k+1）次进入 D2时，速度大小为 1 (2 1)2 k k qUv m   综合上述各式可得 1 1 2 1 2 1 k k k k r v k r v k      整理得 2 2 1 2 1 2 1 k k r k r k    ， 2 2 1 2 1 2 2 1 k k k r r r k      2 1 1 2 (2 1)( ) k k k k rr k r r       同理，对于相邻轨道半径 rk+1，rk+2， 1 2 1k k kr r r     ，整理后有 2 1 1 +1 2 2 (2 1)( ) k k k k rr k r r        由于 rk+2> rk，比较 kr ， 1kr  得 1k kr r   说明随轨道半径 r 的增大，同一盒中相邻轨道的半径之差 r 减小，用同样的方法也可得到 质子在 D1盒中运动时具有相同的结论。 12（2011 四川第 25 题）．（20 分） 如图所示：正方形绝缘光滑水平台面 WXYZ 边长 l =1.8m，距地面 h=0.8m。平行板电容器的极 板 CD 间距 d=0.1m 且垂直放置于台面，C 板位于边界 WX 上，D 板与边界 WZ 相交处有一小孔。 38 电容器外的台面区域内有磁感应强度 B=1T、方向竖直向上的匀强磁场。电荷量 q=5×10-13C 的微粒静止于 W处，在 CD 间加上恒定电压 U=2.5V，板间微粒经电场加速后由 D 板所开小孔 进入磁场（微粒始终不与极板接触），然后由 XY 边界离开台面。在微粒离开台面瞬时，静止 于 X 正下方水平地面上 A点的滑块获得一水平速度，在微粒落地时恰好与之相遇。假定微粒 在真空中运动、极板间电场视为匀强电场，滑块视为质点，滑块与地面间的动摩擦因数  =0.2，取 g=10m/s 2 （1）求微粒在极板间所受电场力的大小并说明两板地极 性； （2）求由 XY 边界离开台面的微粒的质量范围； （3）若微粒质量 mo=1×10 -13 kg，求滑块开始运动时所获 得的速度。 解析： 13（2011 广东第 35 题）、（18 分） 如图 19（a）所示，在以 O 为圆心，内外半径分别为 1R 和 2R 的圆环区域内，存在辐射状电 场和垂直纸面的匀强磁场，内外圆间的电势差 U为常量， 1 0 2 0, 3R R R R  ,一电荷量为+q， 质量为 m 的粒子从内圆上的 A点进入该区域，不计重力。 （1） 已知粒子从外圆上以速度 1v 射出，求粒子在 A 点的初速度 0v 的大小 （2） 若撤去电场，如图 19（b）,已知粒子从 OA 延长线与外圆的交点 C以速度 2v 射出， 39 方向与 OA 延长线成 45°角，求磁感应强度的大小及粒子在磁场中运动的时间 （3） 在图 19（b）中，若粒子从 A 点进入磁场，速度大小为 3v ，方向不确定，要使粒 子一定能够从外圆射出，磁感应强度应小于多少？ 解析： （1）由动能定理：Uq= 2 1 mv1 2 - 2 1 mv0 2 ① 得：v0= m Uqv 22 1  （2）如右图：粒子在磁场中作圆周运动的半径为 r，则 r 2 =2( 2 12 RR  ) 2 ② B1qv2=m r v 2 2 ③ 由②③得：B1= )( 2 12 2 RRq mv  T= r v2 2 ④ t = T   2 2/ ⑤ 由④⑤ t = r v22  （3）由 B2qv3=m R v 2 3 ⑥可知，B越小，R越大。与磁场边界相切的圆的最大半径为 R= 2 21 RR  ⑦ 所以 B2＜ )( 2 12 3 RRq mv  O/ r R V3 40 答案：（1）v0= m Uqv 22 1  （2）B1= )( 2 12 2 RRq mv  t = r v22  （3）B2＜ )( 2 12 3 RRq mv  14（2011北京理综第23题）．（18分） 利用电场和磁场，可以将比荷不同的离子分开，这种方法在化学分析和原子核技术等领域有 重要的应用。 如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场，A处有一狭缝。离子 源产生的离子，经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场，运动 到GA边，被相应的收集器收集。整个装置内部为真空。 已知被加速的两种正离子的质量分别是m1和m2(m1>m2)，电荷量均为q。加速电场的电势差为U， 离子进入电场时的初速度可以忽略。不计重力，也不考虑离子间的相互作用。 (1)求质量为m1的离子进入磁场时的速率v1； (2)当磁感应强度的大小为B时，求两种离子在GA边落点的间距s； (3)在前面的讨论中忽略了狭缝宽度的影响，实际装置中狭缝具有一定宽度。若狭缝过宽， 可能使两束离子在GA边上的落点区域交叠，导致两种离子无法完全分离。 设磁感应强度大小可调，GA边长为定值L，狭缝宽度为d，狭缝右边缘在A处。离子可以从狭 缝各处射入磁场，入射方向仍垂直于GA边且垂直于磁场。为保证上述两种离子能落在GA边上 并被完全分离，求狭缝的最大宽度。 答案． （1）动能定理 2 1 1 1 2 Uq m v 得 1 1 2qUv m  ○1 （2）由牛顿第二定律 2 , mv mvqvB R R qB   ，利用 ○1式得 离子在磁场中的轨道半径为别为 1 1 2 2mUR qB  ， 2 2 2 2m UR qB  ○2 两种离子在 GA 上落点的间距 1 2 1 22 82( ) ( )Us R R m m qB     ○3 （3）质量为m1的离子，在GA边上的落点都在其入射点左侧2R1处，由于狭缝的宽度为d，因此 41 落点区域的宽度也是d。同理，质量为m2的离子在GA边上落点区域的宽度也是d。 为保证两种离子能完全分离，两个区域应无交叠，条件为 1 22( )R R d  ○4 利用○2式，代入○4 式得 2 1 1 2 (1 )mR d m   R1的最大值满足 12 mR L d  得 2 1 ( )(1 )mL d d m    求得最大值 1 2 1 22m m m d L m m    15（2011 山东理综第 25 题）.（18 分） 扭摆器是同步辐射装置中的插入件，能使粒子的运动轨迹发生扭摆。其简化模型如图Ⅰ、Ⅱ 两处的条形均强磁场区边界竖直，相距为 L,磁场方向相反且垂直干扰面。一质量为 m、电量 为-q、重力不计的粒子，从靠近平行板电容器 MN 板处由静止释放，极板间电压为 U,粒子经 电场加速后平行于纸面射入Ⅰ区，射入时速度与水平和方向夹角 30   （1）当Ⅰ区宽度 L1=L、磁感应强度大小 B1=B0时，粒子从Ⅰ区右边界射出时速度与水平方向 夹角也为30，求 B0及粒子在Ⅰ区运动的时间 t0 （2）若Ⅱ区宽度 L2=L1=L 磁感应强度大小 B2=B1=B0，求粒子在Ⅰ区的最高点与Ⅱ区的最低点 之间的高度差 h （3）若 L2=L1=L、B1=B0，为使粒子能返回Ⅰ区，求 B2 应满足的条件 （4）若 1 2 1 2,B B L L  ，且已保证了粒子能从Ⅱ区 右边界射出。为使粒子从Ⅱ区右边界射出的方向与从 Ⅰ区左边界射出的方向总相同，求 B1、B2、L1、、L2、之 间应满足的关系式。 解析： 42 16(重庆第 25 题).（19 分）某仪器用电场和磁场来控制电子在材料表面上方的运动，如题 25 图所示，材料表面上方矩形区域 PP'N'N 充满竖直向下的匀强电场，宽为 d；矩形区域 43 NN'M'M 充满垂直纸面向里的匀强磁场，磁感应强度为 B，长为 3s，宽为 s；NN'为磁场与电 场之间的薄隔离层。一个电荷量为 e、质量为 m、初速为零的电子，从 P点开始被电场加速 经隔离层垂直进入磁场，电子每次穿越隔离层，运动方向不变，其动能损失是每次穿越前动 能的 10%，最后电子仅能从磁场边界 M'N'飞出。 不计电子所受重力。 (1)求电子第二次与第一次圆周运动半径之比； (2)求电场强度的取值范围； (3)A 是MN 的中点，若要使电子在 A、M 间 垂直于 AM 飞出，求电子在磁场区域中运动的 时间。 解： (1)设圆周运动的半径分别为 R1、R2、……、Rn、Rn+1，…，第一和第二次圆周运 动速率分别为 v1和 v2，动能分别为 Ek1和 Ek2 由：Ek2=0.81Ek1，R1= ，R2= 得：R2：R1=0.9 (2)设电场强度为 E．第一次到达隔离层前的速率为 v′ 由： 得： 又由： 得： (3)设电子在匀强磁场中，圆周运动的周期为 T，运动的半圆周个数为 n，运 动总时间为 t， 由题意，有： 得：n=2 44 2011 普通高校招生考试试题汇编-电磁感应 1 (广东卷第15题).将闭合多匝线圈置于仅随时间变化的磁场中，线圈平面与磁场方向垂直， 关于线圈中产生的感应电动势和感应电流，下列表述正确的是 A.感应电动势的大小与线圈的匝数无关 B.穿过线圈的磁通量越大，感应电动势越大 C.穿过线圈的磁通量变化越快，感应电动势越大 D.感应电流产生的磁场方向与原磁场方向始终相同 2(2011 江苏卷第 2题)．如图所示，固定的水平长直导线中通有电流 I，矩形线框与导线在 同一竖直平面内，且一边与导线平行。线框由静止释放，在下落过 程中 A．穿过线框的磁通量保持不变 B．线框中感应电流方向保持不变 C．线框所受安掊力的合力为零 D．线框的机械能不断增大 3(2011 江苏卷第 5 题)．如图所示，水平面内有一平行金属导轨，导 轨光滑且电阻不计。匀强磁场与导轨一闪身垂直。阻值为 R 的导体 棒垂直于导轨静止放置，且与导轨接触。T=0 时，将形状 S 由 1 掷到 2。Q、i、v 和 a 分别表示电容器所带的电荷量、棒中的电流、棒的 速度和加速度。下列图象正确的是 ( D) 4(福建第 17 题). 如图，足够长的 U 型光滑金属导轨平面与水平面成 角（0＜ ＜90°), 其中 MN 平行且间距为 L，导轨平面与磁感应强度为 B 的匀强磁场垂直，导轨电阻不计。金 属棒 ab由静止开始沿导轨下滑，并与两导轨始终保持垂直且良好接触，ab棒接入电路的电 阻为 R，当流过 ab棒某一横截面的电量为 q 时，它的速度大小为 v，则金属棒 ab在这一过 程中 A.F 运动的平均速度大小为 1 2  B.平滑位移大小为 qR BL C.产生的焦尔热为 qBL D.受到的最大安培力大小为 2 2 sinB L R   45 5(海南第 6题).如图，EOF 和 E O F  为空间一匀强磁场的边界，其中 EO∥ E O ，FO∥ F O ， 且 EO⊥OF；OO为∠EOF 的角平分线，OO间的距 离为 l；磁场方向垂直于纸面向里。一边长为 l的正 方形导线框沿OO方向匀速通过磁场，t=0 时刻恰好 位于图示位置。规定导线框中感应电流沿逆时针方向 时为正，则感应电流 i 与实践 t 的关系图线可能正确 的是 ( B ) 6（2011 海南第 7 题）．自然界的电、热和磁等现象都是相互联系的，很多物理学家为寻找 它们之间的联系做出了贡献。下列说法正确的是 A.奥斯特发现了电流的磁效应，揭示了电现象和磁现象之间的联系 B.欧姆发现了欧姆定律，说明了热现象和电现象之间存在联系 C.法拉第发现了电磁感应现象，揭示了磁现象和电现象之间的联系 D.焦耳发现了电流的热效应，定量得出了电能和热能之间的转换关系 解析：考察科学史，选 ACD 7（2011 广东第 15 题）.将闭合多匝线圈置于仅随时间变化的磁场中，线圈平面与磁场方向 垂直，关于线圈中产生的感应电动势和感应电流，下列表述正确的是 A.感应电动势的大小与线圈的匝数无关 B.穿过线圈的磁通量越大，感应电动势越大 C.穿过线圈的磁通量变化越快，感应电动势越大 D.感应电流产生的磁场方向与原磁场方向始终相同 解析：由 E= t BNS t N      ，AB 错，C正确。B 原与 B 感的方向可相同亦可相反。D错。选 C 8（2011北京第19题）．某同学为了验证断电自感现象，自己找来带铁心的线圈L、小灯泡A、 开关S和电池组E，用导线将它们连接成如图所示的电路。检查电路后，闭合开关S，小灯泡 发光；再断开开关S，小灯泡仅有不显著的延时熄灭现象。虽经多次重复，仍未见老师演示 46 时出现的小灯泡闪亮现象，他冥思苦想找不出原因。你认为最有可能造成小灯泡末闪亮的原 因是 A．电源的内阻较大 B．小灯泡电阻偏大 C．线圈电阻偏大 D．线圈的自感系数较大 9 (2011上海第13题)．如图，均匀带正电的绝缘 圆环a与金属圆环b同心共面放置，当a绕O点在其 所在平面内旋转时，b中产生顺时针方向的感应电流，且具有收缩趋 势，由此可知，圆环a (A)顺时针加速旋转 (B)顺时针减速旋转 (C)逆时针加速旋转 (D)逆时针减速旋转 10(2011上海第20题).如图，磁场垂直于纸面，磁感应强度在 竖直方向均匀分布，水平方向非均匀分布。一铜制圆环用丝线 悬挂于O点，将圆环拉至位置 a后无初速释放，在圆环从 a摆 向b的过程中 (A)感应电流方向先逆时针后顺时针再逆时针 (B)感应电流方向一直是逆时针 (C)安培力方向始终与速度方向相反 (D)安培力方向始终沿水平方向 11（201 山东第 22 题）. 如图甲所示，两固定的竖直光滑金属导轨足够长且电阻不计。两质 量、长度均相同的导体棒 c、 d ，置于边界水平的匀强磁场上方同 一高度 h处。磁场宽为 3h，方向与导轨平面垂直。先由静止释放c， c刚进入磁场即匀速运动，此时再由静止释放 d ，两导体棒与导轨 始终保持良好接触。用 ca 表示 c的加速度， kdE 表示 d 的动能， cx 、 dx 分别表示 c、d 相对释放点的位移。图乙中正确的是 答案：BD 解析：开始 c 的加速度为 g，c刚进入磁场即匀速运动，加速度为 0，在 d 下落 h 的过程中， 47 2 2 1 gth  ，c匀速下降了 htgtxc 2 ，d 进入磁场后，c、d 又只在重力作用下运动， 加速度为 g，一起运动了 h，c出磁场，这时 c的加速度仍为 g，因此 A 错误，B 正确；c出 磁场后， d 这时受到重力和向上的安培力，并且合力向上，开始做减速运动，当运动了 2h 后， d 出磁场，又做加速运动，所以 C 错误，D 正确。 12（2011上海第28题）．在“研究回路中感应电动势大小与磁通量变化快慢的关系”实验(见 图(a))中，得到 1/E t  图线如图(b)所示。 (1)(多选题)在实验中需保持不变的是( ) (A)挡光片的宽度 (B)小车的释放位置 (C)导轨倾斜的角度 (D)光电门的位置 (2)线圈匝数增加一倍后重做该实验，在图(b)中画出实验图线。 (1) A，D (3 分) (2)见图 (2 分) 13（2011 全国卷 1 第 24 题）．(15 分) 如图，两根足够长的金属导轨 ab、cd 竖直放置，导轨间距离为 L1电阻不计。在导轨上端并接两个额定功率均为 P、电阻均为 R 的小 灯泡。整个系统置于匀强磁场中，磁感应强度方向与导轨所在平面 垂直。现将一质量为 m、电阻可以忽略的金属棒 MN 从图示位置由静 止开始释放。金属棒下落过程中保持水平，且与导轨接触良好。已 知某时刻后两灯泡保持正常发光。重力加速度为 g。求： (1)磁感应强度的大小： (2)灯泡正常发光时导体棒的运动速率。 解析：每个灯上的额定电流为 PI R  额定电压为： PU R （1）最后 MN 匀速运动故：B2IL=mg 求出： 2 mg PRB PL  48 （2）U=BLv 得： 2PR Pv BL mg   14（2011 海南第 16 题）.如图，ab 和 cd 是两条竖直放置的长直光 滑金属导轨，MN 和 ' 'M N 是两根用细线连接的金属杆，其质量分 别为 m和 2m。竖直向上的外力 F作用在杆 MN 上，使两杆水平静止， 并刚好与导轨接触；两杆的总电阻为 R，导轨间距为 l。整个装置 处在磁感应强度为 B的匀强磁场中，磁场方向与导轨所在平面垂直。 导轨电阻可忽略，重力加速度为 g。在 t=0 时刻将细线烧断，保持 F不变，金属杆和导轨始终接触良好。求 （1）细线少断后，任意时刻两杆运动的速度之比； （2）两杆分别达到的最大速度。 解析：设某时刻 MN 和 ' 'M N 速度分别为 v1、v2。 （1）MN 和 ' 'M N 动量守恒：mv1-2mv2=0 求出： 1 2 2v v  ① （2）当 MN 和 ' 'M N 的加速度为零时，速度最大 对 ' 'M N 受力平衡：BIl mg ② EI R  ③ 1 2E Blv blv  ④ 由①——④得： 1 2 2 2 3 mgRv B l  、 2 2 23 mgRv B l  15（2011 天津第 11 题）．（18 分） 如图所示，两根足够长的光滑金属导轨 MN、PQ 间距为 l=0.5m，其电阻不计，两导轨及其构 成的平面均与水平面成 30°角。完全相同的两金属棒 ab、cd 分别垂直导轨放置，每棒两端 都与导轨始终有良好接触，已知两棒的质量均为 0.02kg，电阻均为 R=0.1Ω，整个装置处在 垂直于导轨平面向上的匀强磁场中，磁感应强度为 B=0.2T，棒 ab 在平行于导轨向上的力 F 作用下，沿导轨向上匀速运动，而棒 cd 恰好能保持静 止。取 g=10m/s2，问： （1）通过 cd 棒的电流 I是多少，方向如何？ （2）棒 ab 受到的力 F 多大？ （3）棒 cd 每产生 Q=0.1J 的热量，力 F做的功 W 是多 少？ 解析：（1）棒 cd 受到的安培力 cdF IlB ① 49 棒 cd 在共点力作用下平衡，则 sin30cdF mg  ② 由①②式代入数据解得 I=1A，方向由右手定则可知由 d 到 c。 （2）棒 ab 与棒 cd 受到的安培力大小相等 Fab=Fcd 对棒 ab 由共点力平衡有 sin30F mg IlB  ③ 代入数据解得 F=0.2N ④ （3）设在时间 t 内棒 cd 产生 Q=0.1J 热量，由焦耳定律可知 2Q I Rt ⑤ 设 ab 棒匀速运动的速度大小为 v，则产生的感应电动势 E=Blv ⑥ 由闭合电路欧姆定律知 2 EI R  ⑦ 由运动学公式知，在时间 t 内，棒 ab 沿导轨的位移 x=vt ⑧ 力 F 做的功 W=Fx ⑨ 综合上述各式，代入数据解得 W=0.4J 16（2011 浙江第 23 题）.（16 分） 如图甲所示，在水平面上固定有长为 L=2m、宽为 d=1m 的金属“U”型轨导，在“U”型导轨 右侧 l=0.5m 范围内存在垂直纸面向里的匀强磁场，且磁感应强度随时间变化规律如图乙所 示。在 t=0 时刻，质量为 m=0.1kg 的导体棒以 v0=1m/s 的初速度从导轨的左端开始向右运动， 导体棒与导轨之间的动摩擦因数为μ=0.1，导轨与导体棒单位长度的电阻均为 m/1.0  ，不计导体棒与导轨之间的接触电阻及地球磁场的影响（取 2/10 smg  ）。 （1）通过计算分析 4s 内导体棒的运动情况； （2）计算 4s 内回路中电流的大小，并判断电流方向； （3）计算 4s 内回路产生的焦耳热。 答案：（1）导体棒在 s1 前做匀减速运动，在 s1 后以后一直保持静止。 （2） A2.0 ，电流方向是顺时针方向。 （3） J04.0 50 解析：（1）导体棒先在无磁场区域做匀减速运动，有 mamg   atvvt  0 20 2 1 attvx  代入数据解得： st 1 ， mx 5.0 ，导体棒没有进入磁场区域。 导体棒在 s1 末已经停止运动，以后一直保持静止，离左端位置仍为 mx 5.0 （2）前 s2 磁通量不变，回路电动势和电流分别为 0E ， 0I 后 s2 回路产生的电动势为 V t Bld t E 1.0        回路的总长度为 m5 ，因此回路的总电阻为  5.05R 电流为 A R EI 2.0 根据楞次定律，在回路中的电流方向是顺时针方向 （3）前 s2 电流为零，后 s2 有恒定电流，焦耳热为 JRtIQ 04.02  17（2011上海第32题）．(14 分) 电阻可忽略的光滑平行金属导轨长S=1.15m，两导轨间距L=0.75 m，导轨倾角为30°，导轨 上端ab接一阻值R=1.5Ω的电阻，磁感应强度B=0.8T的匀强磁场垂直轨道平面向上。阻值 r=0.5Ω，质量m=0.2kg的金属棒与轨道垂直且接触良好，从轨道上端ab处由静止开始下滑至 底端，在此过程中金属棒产生的焦耳热 0.1rQ J 。(取 210 /g m s )求： (1)金属棒在此过程中克服安培力的功W安 ； (2)金属棒下滑速度 2 /v m s 时的加速度 a． (3)为求金属棒下滑的最大速度 mv ，有同学解答如下：由动能定理 21- = 2 mW W mv重 安 ，……。 由此所得结果是否正确？若正确，说明理由并完成本小题；若不正确，给出正确的解答。 答案.（1）下滑过程中安培力的功即为在电阻上产生的焦耳热，由于 3R r ，因此 3 0.3( )R rQ Q J  （1 分） ∴ = 0.4( )R rW Q Q Q J  安 （2）金属棒下滑时受重力和安培力 2 2 = B LF BIL v R r  安 （1 分） 由牛顿第二定律 2 2 sin 30 B Lmg v ma R r     （3分） 51 ∴ 2 2 2 2 21 0.8 0.75 2sin 30 10 3.2( / ) ( ) 2 0.2 (1.5 0.5) B La g v m s m R r            （2分） (3)此解法正确。 (1 分) 金属棒下滑时舞重力和安培力作用，其运动满足 2 2 sin 30 B Lmg v ma R r     上式表明，加速度随速度增加而减小，棒作加速度减小的加速运动。无论最终是否达到匀速， 当棒到达斜面底端时速度一定为最大。由动能定理可以得到棒的末速度，因此上述解法正确。 (2 分) 21sin 30 2 mmgS Q mv   （1 分） ∴ 2 1 2 0.42 sin 30 2 10 1.15 2.74( / ) 2 0.2m Qv gS m s m          （1分） 18(四川第 24 题).（19 分） 如图所示，间距 l=0.3m 的平行金属导轨 a1b1c1和 a2b2c2分别固定在两个竖直面内，在水 平面 a1b1b2a2区域内和倾角 = 37 的斜面 c1b1b2c2区域内分别有磁感应强度 B1=0.4T、方向竖 直向上和 B2=1T、方向垂直于斜面向上的匀强磁场。电阻 R=0.3、质量 m1=0.1kg、长为 l 的 相同导体杆 K、S、Q 分别放置在导轨上，S 杆的两端固定在 b1、b2点，K、Q 杆可沿导轨无摩 擦滑动且始终接触良好。一端系于 K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂，绳上 穿有质量 m2=0.05kg 的小环。已知小环以 a=6 m/s 2 的加速度沿绳下滑，K 杆保持静止，Q 杆 在垂直于杆且沿斜面向下的拉力 F作用下匀速运动。不计导轨电阻和滑轮摩擦，绳不可伸长。 取 g=10 m/s2，sin 37 =0.6，cos 37 =0.8。求 （1）小环所受摩擦力的大小； （2）Q杆所受拉力的瞬时功率。 解析： 以小环为研究对象，由牛 顿第二定律 ① 代 入 数 据 得 ② 设流过杆 K 的电流为 ，由平衡条件得 ③ 对杆 Q，根据并联电路特点以及平衡条件得 ④ 由法拉第电磁感应定律的推论得 ⑤ 52 根据欧姆定律有 ⑥ 且 ⑦ 瞬时功率表达式为 ⑧ 联立以上各式得 ⑨ 【答案】（1） ；（2） 。 19(重庆第 23 题).（16 分） 有人设计了一种可测速的跑步机，测速原理如题 23 图所示，该机底面固定有间距为 L、长 度为 d 的平行金属电极。电极间充满磁感应强度为 B、方向垂直纸面向里的匀强磁场，且 接有电压表和电阻 R ,绝缘橡胶带上镀有间 距为 d 的平行细金属条，磁场中始终仅有一 根金属条，且与电极接触良好，不计金属电 阻，若橡胶带匀速运动时，电压表读数为U , 求： （1）橡胶带匀速运动的速率； （2）电阻 R 消耗的电功率； （3）一根金属条每次经过磁场区域克服安培力做的功。 解： (l)设电动势为 ，橡胶带运动速率为 v 由： 得： (2)设电功率为 P (3)设电流强度为 I，安培力为 F．克服安培力做的功为 W 由： 得： 53 2011 普通高校招生试题汇编：功和能的关系 1 (2011 江苏第 4 题)．如图所示，演员正在进行杂技表演。由图可估 算出他将一只鸡蛋抛出的过程中对鸡蛋所做的功最接近于 A．0.3J B．3J C．30J D．300J 2（2011 全国卷 1 第 20 题）．质量为 M、内壁间距为 L 的箱子静止于光滑的水平面上，箱子 中间有一质量为 m 的小物块，小物块与箱子底板间的动摩擦因数为μ。初始时小物块停在箱 子正中间，如图所示。现给小物块一水平向右的初速度 v，小物块与箱壁碰撞 N 次后恰又回 到箱子正中间，井与箱子保持相对静止。设碰撞都是弹性的，则整个过程中，系统损失的动 能为 A． 21 2 mv B． 21 2 mM v m M C． 1 2 N mgL D． N mgL 解析：两物体最终速度相等设为 u由动量守恒得：mv=(m+M)u, 系统 损失的动能为： 2 2 21 1 1( ) 2 2 2 mMmv m M u v m M     系统损失的动能转化为 内能 Q=fs=N mgL 3．(四川第 19 题).如图是“神舟”系列航天飞船返回舱返回 地面的示意图，假定其过程可简化为：打开降落伞一段时间后， 整个装置匀速下降，为确保安全着陆，需点燃返回舱的缓冲火 箭，在火箭喷气过程中返回舱做减速直线运动，则 A.火箭开始喷气瞬间伞绳对返回舱的拉力变小 B.返回舱在喷气过程中减速的住要原因是空气阻力 C返回舱在喷气过程中所受合外力可能做正功 D.返回舱在喷气过程中处于失重状态 解析：先从力学角度讨论 A．B 两项；而 C 项宜用动能定理；D项则考查超重、失重概念。 答案选 A。由整体法、隔离法结合牛顿第二定律，可知 A正确 B 错；由动能定理可知 C 错； 因为物体具有竖直向上的加速度，因此处于超重状态，D错。 4(四川第 21 题)．质量为 m的带正电小球由空中 A点无初速度自由下落，在 t 秒末加上竖直 向上、范围足够大的匀强电场，再经过 t 秒小球又回到 A 点，不计空气阻力且小球从末落地， 则 A.整个过程中小球电势能变换了 2 23 2 mg t ？ B.整个过程中小球动量增量的大小为 2mgt C.从加电场开始到小球运动到最低点时小球动能变化了 mg2t2 D.从 A 点到最低点小球重力势能变化了 2 3 mg 2 t 2 解析：选 BD。从运动学公式（平均速度等）入手，可求出两次过程的末速度比例、加速度 54 比例，做好准备工作。通过动能定律、机械能守恒定律等得出电场力做功，再由功能关系可 知电势能增减以及动能变化等，从而排除 A．C 两项；借助运动学公式，选项 B 中的动量变 化可直接计算；对于选项 D，要先由运动学公式确定 ，再结合此前的机械能守恒定律来 计算重力势能变化量。 运动过程如上图所示，分析可知，加电场之前与加电场之后，小球的位移大 小是相等的。由运动学公式 得 。对加电场之后 的运动过程应用动能定理得 ，对此前的过程有机 械能守恒 ，以及运动学公式 。由以上各式联立可得 ，即整个过程中小球电势能减少了 ， A错；动量增量为 ，可知 B 正确；从加电场开始到小球运动到 最低点时， ，C 错；由运动学公式知 ， 以 及 ， 则 从 A 点 到 最 低 点 小 球 重 力 势 能 变 化 量 为 ，D正确。 5．（2011 海南第 9 题）.一质量为 1kg 的质点静止于光滑水平面上，从 t=0 时起，第 1秒内 受到 2N 的水平外力作用，第 2 秒内受到同方向的 1N 的外力作用。下列判断正确的是 A. 0～2s 内外力的平均功率是 9 4 W B.第 2 秒内外力所做的功是 5 4 J C.第 2 秒末外力的瞬时功率最大 D.第 1秒内与第 2 秒内质点动能增加量的比值是 4 5 解析：由动量定理求出 1s 末、2s 末速度分别为：v1=2m/s、v2=3m/s 故合力做功为 w= 21 4.5 2 mv J 功率为 4.5 1.5 3 wp w w t    1s 末、2s 末功率分别为：4w、3w 第 1 秒内 55 与第 2秒动能增加量分别为： 2 1 1 2 2 mv J 、 2 2 2 1 1 1 2.5 2 2 mv mv J  ，比值：4：5 6（2011 新课标理综第 16 题）.一蹦极运动员身系弹性蹦极绳从水面上方的高台下落，到最 低点时距水面还有数米距离。假定空气阻力可忽略，运动员可视为质点，下列说法正确的是 （ABC） A. 运动员到达最低点前重力势能始终减小 B. 蹦极绳张紧后的下落过程中，弹性力做负功，弹性势能增加 C. 蹦极过程中，运动员、地球和蹦极绳所组成的系统机械能守恒 D. 蹦极过程中，重力势能的改变与重力势能零点的选取有关 解析：主要考查功和能的关系。运动员到达最低点过程中，重力做正功，所以重力势能始终 减少，A 项正确。蹦极绳张紧后的下落过程中，弹性力做负功，弹性势能增加，B 项正确。 蹦极过程中，运动员、地球和蹦极绳所组成的系统，只有重力和弹性力做功，所以机械能守 恒，C项正确。重力势能的改变与重力势能零点选取无关，D 项错误。 7（2011 全国理综第 18 题）.电磁轨道炮工作原理如图所示。待发射弹体可在两平行轨道之 间自由移动，并与轨道保持良好接触。电流 I从一条轨道流入，通过导电弹体后从另一条轨 道流回。轨道电流可形成在弹体处垂直于轨道面得磁场（可视为匀强磁场），磁感应强度的 大小与 I 成正比。通电的弹体在轨道上受到安培力的作用而高速射出。现欲使弹体的出射速 度增加至原来的 2 倍，理论上可采用的方 法是（BD） A.只将轨道长度 L 变为原来的 2 倍 B.只将电流 I 增加至原来的 2倍 C.只将弹体质量减至原来的一半 D.将弹体质量减至原来的一半，轨道长度 L变为原来的 2倍，其它量不变 解析：主要考查动能定理。利用动能定理 有 2 2 1 mvBIlL  ,B=kI 解 得 m lLkIv 22  。所以正确答案是 BD。 8 (2011上海15)．如图，一长为 L的轻杆一端固定在光滑铰链上，另一端固定一质量为m的 小球。一水平向右的拉力作用于杆的中点，使杆以角速度匀速转动，当杆与水平方向成 60°时，拉力的功率为 (A) mgL (B) 3 2 mgL (C) 1 2 mgL (D) 3 6 mgL 答案：C 9（2011 山东第 18 题）.如图所示，将小球 a从地面以初速度 v。竖直上抛的同时，将另一 56 相同质量的小球b从距地面 h处由静止释放，两球恰在 2 h 处相遇（不计 空气阻力）。则 A.两球同时落地 B.相遇时两球速度大小相等 C.从开始运动到相遇，球 a动能的减少量等于球b动能的增加量 D.相遇后的任意时刻，重力对球 a做功功率和对球b做功功率相等 答案：C 解析：相遇时满足 hgttvgt  2 0 2 2 1 2 1 ， 22 1 2 hgt  ，所以 ghv 2 0 ，小球 a落地时间 g hta 2  ，球b落地时间 g h g gh g v tb 222 0  ，因此A错误；相遇时， 2 2 hgva  ， 2 22 0 2 hgvvb  ， 0bv ，所以 B 错误；因为两球恰在 2 h 处相遇，说明重力做功的数值相 等，根据动能定理，球 a动能的减少量等于球b动能的增加量，C正确；相遇后的任意时刻， 球 a的速度始终大于球b的速度，因此重力对球 a做功功率大于对球b做功功率，D错误。 10（2011 海南第 14 题）.现要通过实验验证机械能守恒定律。实验装置如图 1 所示：水平 桌面上固定一倾斜的气垫导轨；导轨上 A点处有一带长方形遮光片的滑块，其总质量为 M， 左端由跨过轻质光滑定滑轮的细绳与一质量为 m的砝码相连；遮光片两条长边与导轨垂直； 导轨上 B 点有一光电门，可以测试遮光片经过光电门时的挡光时间 t，用 d 表示 A点到导轨 低端 C 点的距离，h 表示 A 与 C 的高度差，b 表示遮光片的宽 度，s 表示 A ,B 两点的距离，将遮光片通过光电门的平均速 度看作滑块通过 B 点时的瞬时速度。用 g 表示重力加速度。 完成下列填空和作图； （1）若将滑块自 A 点由静止释放，则在滑块从 A运动至 B 的 过程中，滑块、遮光片与砝码组成的系统重力势能的减小量可表示为____ ( )h M m gs d  。 动能的增加量可表示为__ 2 2 1 ( ) 2 bm M t  。若在运动过程中机械能守恒， 2 1 t 与 s的关系式为 2 1 t __ 2 2 1 2( ) ( ) hM dm g s t M m db    (2)多次改变光电门的位置，每次均令滑块自同一点（A 点）下滑，测量相应的 s 与 t 值， b v0 h h/2 a 57 结果如下表所示： 以 s为横坐标， 2 1 t 为纵坐标，在答题卡上对应图 2 位置的坐标纸中描出第 1 和第 5 个数据 点；根据 5个数据点作直线，求得该直线的斜率 k=________2.40___ 214 .10   sm (保留 3 位有效数字). 由测得的 h、d、b、M 和 m 数值可以计算出 2 1 s t  直线的斜率 ok ，将 k和 ok 进行比较，若其 差值在试验允许的范围内，则可认为此试验验证了机械能守恒定律。 11(上海第33 题)．(14 分)如图(a)，磁铁A、B的同名磁极相对放置，置于水平气垫导轨上。 A固定于导轨左端，B的质量m=0.5kg，可在导轨上无摩擦滑动。将B在A附近某一位置由静止 释放，由于能量守恒，可通过测量B在不同位置处的速度， 得到B的势能随位置x的变化规律，见图(c)中曲线I。若将 导轨右端抬高，使其与水平面成一定角度(如图(b)所示)， 则B的总势能曲线如图(c)中II所示，将B在 20.0x cm 处由 静止释放，求：(解答时必须写出必要的推断说明。取 29.8 /g m s ) (1)B在运动过程中动能最大的位置； (2)运动过程中B的最大速度和最大位移。 (3)图(c)中直线III为曲线II的渐近线，求导轨的倾角。 (4)若A、B异名磁极相对放置，导轨的倾角不变，在图(c)上画出B的总势能随x的变化曲线． 58 答案．(14 分) (1)势能最小处动能最大 (1 分) 由图线 II 得 6.1( )x cm (2 分) (在 5.9 ~ 6.3cm 间均视为正确) (2) 由 图 读 得 释 放 处 势 能 0.90pE J ，此即 B 的总能量。出 于运动中总能量守恒，因此在势能最 小处动能最大，由图像得最小势能为 0.47J，则最大动能为 0.9 0.47 0.43( )kmE J   （2 分) ( kmE 在 0.42 ~ 0.44J 间均视为正确) 最大速度为 2 2 0.43 1.31( / ) 0.5 km m Ev m s m     (1 分) ( mv 在 1.29～1.33 m／s 间均视为正确) x=20.0 cm处的总能量为 0.90J，最大位移由 E=0.90J的水平直线与曲线 II的左侧交点确定, 由图中读出交点位置为 x=2.0cm，因此，最大位移 20.0 2.0 18.0( )x cm    (2 分) ( x 在 17.9~18.1cm 间均视为正确) (3)渐近线 III 表示 B 的重力势能随位置变化关系，即 sinPgE mgx kx  （2分) ∴ sin k mg   由图读出直线斜率 20.85 0.30 4.23 10 ( / ) 20.0 7.0 k J cm     2 1 110 4.23sin ( ) sin 59.7 0.5 9.8 k mg         （1 分） （ 在59 ~ 61 间均视为正确） （4）若异名磁极相对放置，A，B 间相互作用势能为负值，总势能如图。 （2 分） 59 12(江苏第 14 题)．(16 分)如图所示，长为 L、内壁光滑的直管与水平地面成 30°角固定放 置。将一质量为 m 的小球固定在管底，用一轻质光滑细线将小球与质量为 M=km 的小物块相 连，小物块悬挂于管口。现将小球释放，一段时间后，小物块落地静止不动，小球继续向上 运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变。(重力加速度为 g) (1)求小物块下落过程中的加速度大小； (2)求小球从管口抛出时的速度大小； (3)试证明小球平抛运动的水平位移总小于 2 2 L 解析： 60 13(福建第 21 题).（19 分） 如图为某种鱼饵自动投放器中的投饵管装置示意图，其下半部 AB 是一长为 2R 的竖直细管，上半部 BC 是半径为 R 的四分之一 圆弧弯管，管口沿水平方向，AB 管内有一原长为 R、下端固定 的轻质弹簧。投饵时，每次总将弹簧长度压缩到 0.5R 后锁定， 在弹簧上段放置一粒鱼饵，解除锁定，弹簧可将鱼饵弹射出去。 设质量为 m 的鱼饵到达管口 C 时，对管壁的作用力恰好为零。 不计鱼饵在运动过程中的机械能损失，且锁定和解除锁定时， 均不改变弹簧的弹性势能。已知重力加速度为 g。求： (1)质量为 m 的鱼饵到达管口 C 时的速度大小 v1; (2)弹簧压缩到 0.5R 时的弹性势能 Ep; （3） 已知地面欲睡面相距 1.5R，若使该投饵管绕 AB 管的中 轴线 OO-。在 角的范围内来回缓慢转动，每次弹射时只放置一粒鱼饵，鱼饵的质量在 到 m 之间变化，且均能落到水面。持续投放足够长时间后，鱼饵能够落到水面的最大面积 S 是多少？ 解析：此题考查平抛运动规律、牛顿运动定律、竖直面内的圆周运动、机械能守恒定律等知 识点 （1）质量为 m 的鱼饵到达管口 C 时做圆周运动的向心力完全由重力提供，则 (1) 解得 (2) (2)弹簧的弹性势能全部转化为鱼饵的机械能，由机械能守恒定律有 61 …………………..(3) 由（2）（3）得 ………………….(4) (3)不考虑因缓慢转动装置对鱼饵速度大小的影响，质量为 m的鱼饵离开管口 C 后做平抛运 动，设经过 t 时间落到水面上，离 OO’的水平距离为 x1，由平抛规律有 ………………………..(5) ………………………(6) 由 （5）（6）两式得 ………………..(7) 当鱼饵的质量为 时，设其到达管口 C 时速度大小为 V2，由机械能守恒定律有 …………………..(8) 由 （4）（8）两式解得 ……………………..(9) 质量为 的鱼饵落到水面时上时，设离 OO’的水平距离为 x2则 ……………………………..(10) 由（5）（9）（10）解得： 鱼饵能够落到水面的最大面积 S，S= (πx2 2 -πx1 2 )= πR2 （或 8.25πR2 ）。 14（2011 安徽 24）．（20 分） 如图所示，质量 M=2kg 的滑块套在光 滑的水平轨道上，质量 m=1kg 的小球通过 长L=0.5m的轻质细杆与滑块上的光滑轴O 连接，小球和轻杆可在竖直平面内绕 O轴 自由转动，开始轻杆处于水平状态，现给 小球一个竖直向上的初速度 v0=4 m/s，g 取 10m/s 2 。 （1）若锁定滑块，试求小球通过最高点 P 时对轻杆的作用力大小和方向。 M m v0 O P L 62 （2）若解除对滑块的锁定，试求小球通过最高点时的速度大小。 （3）在满足（2）的条件下，试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。 解析：（1）设小球能通过最高点，且此时的速度为 v1。在上升过程中，因只有重力做功，小 球的机械能守恒。则 2 2 1 0 1 1 2 2 mv mgL mv  ① 1 6 /v m s ② 设小球到达最高点时，轻杆对小球的作用力为 F，方向向下，则 2 1vF mg m L   ③ 由②③式，得 F=2N ④ 由牛顿第三定律可知，小球对轻杆的作用力大小为 2N，方向竖直向上。 （2）解除锁定后，设小球通过最高点时的速度为 v2，此时滑块的速度为 V。在上升过 程中，因系统在水平方向上不受外力作用，水平方向的动量守恒。以水平向右的方向 为正方向，有 2 0mv MV  ⑤ 在上升过程中，因只有重力做功，系统的机械能守恒，则 2 2 2 2 0 1 1 1 2 2 2 mv MV mgL mv   ⑥ 由⑤⑥式，得 v2=2m/s ⑦ （3）设小球击中滑块右侧轨道的位置点与小球起始点的距离为 s1，滑块向左移动的距 离为 s2，任意时刻小球的水平速度大小为 v3，滑块的速度大小为 V / 。由系统水平方向 的动量守恒，得 3 0mv MV   ⑦ 将⑧式两边同乘以 t ，得 3 0mv t MV t    ⑨ 因⑨式对任意时刻附近的微小间隔 t 都成立，累积相加后，有 1 2 0ms Ms  ○10 又 1 2 2s s L  ○11 由 ○10 ○11 式 得 1 2 3 s m ○12 15（2011 全国卷 1 第 26 题）.（20 分） 装甲车和战舰采用多层钢板比采用同样质量的单 层钢板更能抵御穿甲弹的射击。 通过对一下简化模型的计算可以粗略说明其原因。 质量为 2m、厚度为 2d 的钢板静止在水平光滑桌面 63 上。质量为 m 的子弹以某一速度垂直射向该钢板，刚好能将钢板射穿。现把钢板分成厚度均 为 d、质量均为 m 的相同两块，间隔一段距离水平放置，如图所示。若子弹以相同的速度垂 直射向第一块钢板，穿出后再射向第二块钢板，求子弹射入第二块钢板的深度。设子弹在钢 板中受到的阻力为恒力，且两块钢板不会发生碰撞不计重力影响。 解析：设子弹的初速为 v0,穿过 2d 厚度的钢板时共同速度为：v 受到阻力为 f. 对系统由动量和能量守恒得： 0 ( 2 )mv m m v  ① 2 2 0 1 12 ( 2 ) 2 2 f d mv m m v    ② 由①②得： 2 0 1 6 fd mv ③ 子弹穿过第一块厚度为 d 的钢板时，设其速度为 v1，此时钢板的速度为 u，穿第二块厚度 为 d 的钢板时共用速度为 v2，穿过深度为 d ， 对子弹和第一块钢板系统由动量和能量守恒得： 0 1mv mv mu  ④ 2 2 2 0 1 1 1 1 2 2 2 fd mv mv mu   ⑤ 由③④⑤得： 1 0 1 3 3 ( ) 6 v v v u   故只取一个 ⑥ 对子弹和第二块钢板系统由动量和能量守恒得： 1 2( )mv m m v  ⑦ 2 2 1 2 1 1 ( ) 2 2 f d mv m m v    ⑧ 由③⑥⑦⑧得： 2 3 4 d d  16（2011 天津第 10 题）．（16 分） 如图所示，圆管构成的半圆形竖直轨道固定在水平 地面上，轨道半径为 R，MN 为直径且与水平面 垂直，直径略小于圆管内径的小球 A 以某一初 速度冲进轨道，到达半圆轨道最高点 M 时与静 止于该处的质量与 A 相同的小球 B 发生碰撞， 碰后两球粘在一起飞出轨道，落地点距 N 为 2R。重力加速度为 g，忽略圆管内径，空气 阻力及各处摩擦均不计，求： 64 （1）粘合后的两球从飞出轨道到落地的时间 t； （2）小球 A 冲进轨道时速度 v 的大小。 解析：（1）粘合后的两球飞出轨道后做平抛运动，竖直方向分运动为自由落体运动，有 212 2 R gt ① 解得 2 Rt g  ② （2）设球 A 的质量为 m，碰撞前速度大小为 v1，把球 A冲进轨道最低点时的重力势能定为 0， 由机械能守恒定律知 2 2 1 1 1 2 2 2 mv mv mgR  ③ 设碰撞后粘合在一起的两球速度大小为 v2，由动量守恒定律知 1 22mv mv ④ 飞出轨道后做平抛运动，水平方向分运动为匀速直线运动，有 22R v t ⑤ 综合②③④⑤式得 2 2 2v gR 17（2011 浙江第 24 题）.（20 分）节能混合动力车是一种可以利用汽油及所储存电能作为 动力来源的汽车。有一质量 m=1000kg 的混合动力轿车，在平直公路上以 hkmv /901  匀速 行驶，发动机的输出功率为 kWP 50 。当驾驶员看到前方有 80km/h 的限速标志时，保持 发动机功率不变，立即启动利用电磁阻尼带动的发电机工作给电池充电，使轿车做减速运动， 运动 L=72m 后，速度变为 hkmv /722  。此过程中发动机功率的 5 1 用于轿车的牵引， 5 4 用 于供给发电机工作，发动机输送给发电机的能量最后有 50%转化为电池的电能。假设轿车在 上述运动过程中所受阻力保持不变。求 （1）轿车以 hkm /90 在平直公路上匀速行驶时，所受阻力 阻F 的大小； （2）轿车从 hkm /90 减速到 hkm /72 过程中，获得的电能 电E ； （3）轿车仅用其在上述减速过程中获得的电能 电E 维持 hkm /72 匀速运动的距离 L。 解析：（1）汽车牵引力与输出功率的关系 vFP 牵 将 kWP 50 ， smhkmv /25/901  代入得 N v PF 3 1 102牵 当轿车匀速行驶时，牵引力与阻力大小相等，有 NF 3102阻 65 （2）在减速过程中，注意到发动机只有 P 5 1 用于汽车的牵引，根据动能定理有 2 1 2 2 2 1 2 1 5 1 mvmvLFPt  阻 ，代入数据得 JPt 510575.1  电源获得的电能为 JPtE 4103.6 5 45.0 电 (3)根据题设，轿车在平直公路上匀速行驶时受到的阻力仍为 NF 3102阻 。此过程中， 由能量转化及守恒定律可知，仅有电能用于克服阻力做功 LFE  阻电 ， 代入数据得 mL 5.31 18（2011 广东第 36 题）、（18 分）如图 20 所示，以 A、B 和 C、D 为端点的两半圆形光滑轨 道固定于竖直平面内，一滑板静止在光滑水平地面上，左端紧靠 B 点，上表面所在平面与两 半圆分别相切于 B、C。一物块被轻放在水平匀速运动的传送带上 E 点，运动到 A 时刚好与 传送带速度相同，然后经 A 沿半圆轨道滑下，再经 B 滑上滑板。滑板运动到 C 时被牢固粘连。 物块可视为质点，质量为 m，滑板质量 M=2m，两半圆半径均为 R，板长 l =6.5R，板右端到 C 的距离 L 在 R＜L＜5R 范围内取值。E 距 A 为 S=5R，物块与传送带、物块与滑板间的动摩 擦因素均为μ=0.5，重力加速度取 g. (1)求物块滑到 B 点的速度大小； (2)试讨论物块从滑上滑板到离开滑板右端的过程中，克服摩擦力做的功 Wf与 L的关系，并 判断物块能否滑到 CD 轨道的中点。 解析： （1）μmgs+mg·2R= 2 1 mvB 2 ① 所以 vB=3 Rg （2）设 M 滑动 x1,m 滑动 x2二者达到共同速度 v,则 mvB=(M+m)v ② μmgx1= 2 1 mv 2 ③ —μmgx2= 2 1 mv 2 — 2 1 mvB 2 ④ 由②③④得 v= Rg , x1=2R, x2=8R 66 二者位移之差△x= x2—x1=6R＜6.5R，即滑块未掉下滑板 讨论： R＜L＜2R 时，Wf=μmg(l+L)= 2 1 mg（6.5R+L） 2R≤L＜5R 时，Wf=μmgx2+μmg(l—△x)=4.25mgR＜4.5mgR，即滑块速度不为 0，滑上右侧轨 道。 要使滑块滑到 CD 轨道中点，vc必须满足： 2 1 mvc 2 ≥mgR ⑤ 此时 L应满足：μmg(l+L) ≤ 2 1 mvB 2 — 2 1 mvc 2 ⑥ 则 L≤ 2 1 R，不符合题意，滑块不能滑到 CD 轨道中点。 答案：（1） vB=3 Rg （2） ①R＜L＜2R 时，Wf=μmg(l+L)= 2 1 mg（6.5R+L） ②2R≤L＜5R 时，Wf=μmgx2+μmg(l—△x)=4.25mgR＜4.5mgR，即滑块速度不为 0，滑上右侧 轨道。 滑块不能滑到 CD 轨道中点 19（2011北京第22题）．（16分） 如图所示，长度为l的轻绳上端固定在O点，下端系一质量为m 的小球（小球的大小可以忽略）。 （1）在水平拉力F的作用下，轻绳与竖直方向的夹角为α， 小球保持静止。画出此时小球的受力图，并求力F的大小； （2）由图示位置无初速释放小球，求当小球通过最低点 时的速度大小及轻绳对小球的拉力。不计空气阻力。 答案：（1）受力图见右 根据平衡条件，的拉力大小F=mgtanα （2）运动中只有重力做功，系统机械能守恒 21(1 cos ) 2 mgl mv  则通过最低点时，小球的速度大小 2 (1 cos )v gl   根据牛顿第二定律 2vT mg m l    解得轻绳对小球的拉力 l m O F α T F mg 67 2 (3 2cos )vT mg m mg l      ，方向竖直向上 2011 普通高考试题汇编：静电场 1 (2011 江苏经 8 题)．一粒子从 A 点射入电场，从 B 点射 出，电场的等势面和粒子的运动轨迹如图所示，图中左侧前 三个等势面彼此平行，不计粒子的重力。下列说法正确的有 A．粒子带负电 B．粒子的加速度先不变，后变小 C．粒子的速度不断增大 D．粒子的电势能先减小，后增大 2（2011 安徽第 18 题）．图（a）为示管的原理图。如果在电极 YY’之间所加的电压图按图 （b）所示的规律变化，在电极 XX’ 之间所加的电压按图（c）所示的规律变化，则在荧光 屏上会看到的图形是 答案：B 解析：由于电极 XX’加的是扫描电压，电极 YY’之间所加的电压信号电压，所以荧光屏上 会看到的图形是 B，答案 B 正确。 3（2011 安徽第 20 题）．如图（a）所示，两平行正对的金属板 A、B 间加有如图（b）所示 的交变电压，一重力可忽略不计的带正电粒 子被固定在两板的正中间 P 处。若在 t0时刻 释放该粒子，粒子会时而向 A 板运动，时而 向 B 板运动，并最终打在 A 板上。则 t0可能 属于的时间段是 A． 00 4 Tt  B． 0 3 2 4 T Tt  C． 0 3 4 T t T  D． 0 9 8 TT t  答案：B 解析：若 00 4 Tt  ，带正电粒子先加速向 B 板运动、再减速运动至零；然后再反方向加速 亮 荧光屏 Y Y XX X Y Y 偏 转 电 电 子 X ttt1 2 t1 2 t1 3 t1 t1 U x U y O O 图 图(b) 图 A B C D P t UAB UO -UO O T/2 T A B 图(a) 图(b) 68 运动、减速运动至零；如此反复运动，每次向右运动的距离大于向左运动的距离，最终打在 B 板上，所以 A 错误。若 0 3 2 4 T Tt  ，带正电粒子先加速向 A 板运动、再减速运动至零； 然后再反方向加速运动、减速运动至零；如此反复运动，每次向左运动的距离大于向右运动 的距离，最终打在 A 板上，所以 B 正确。若 0 3 4 T t T  ，带正电粒子先加速向 A 板运动、 再减速运动至零；然后再反方向加速运动、减速运动至零；如此反复运动，每次向左运动的 距离小于向右运动的距离，最终打在 B 板上，所以 C 错误。若 0 9 8 TT t  ，带正电粒子先 加速向 B 板运动、再减速运动至零；然后再反方向加速运动、减速运动至零；如此反复运动， 每次向右运动的距离大于向左运动的距离，最终打在 B 板上，所以 D 错误。 4（2011 全国卷 1 第 17 题）．通常一次闪电过程历时约 0.2～O.3s，它由若干个相继发生的 闪击构成。每个闪击持续时间仅 40～80μs，电荷转移主要发生在第一个闪击过程中。在某 一次闪电前云地之间的电势差约为 1.0× 910 v，云地间距离约为 l km；第一个闪击过程中 云地间转移的电荷量约为 6 C，闪击持续时间约为 60μs。假定闪电前云地间的电场是均匀 的。根据以上数据，下列判断正确的是 A.闪电电流的瞬时值可达到 1× 510 A B．整个闪电过程的平均功率约为 l× 1410 W C．闪电前云地间的电场强度约为 l×10 6 V/m D.整个闪电过程向外释放的能量约为 6× 610 J 解析： 5 6 6 10 60 10 qI A A t     9 6 3 10 / 10 / 10 uE v m v m d    96 10w Uq J   9 14 6 6 10 10 60 10 wp w w t       5（2011 海南第 1 题）.关于静电场，下列说法正确的是 A. 电势等于零的物体一定不带电 B. 电场强度为零的点，电势一定为零 C. 同一电场线上的各点，电势一定相等 D. 负电荷沿电场线方向移动时，电势能一定增加 解析：考察电场和电势概念，选 D 6（2011 海南第 3 题）.三个相同的金属小球 1.2.3.分别置于绝缘支架上，各球之间的距离 远大于小球的直径。球 1 的带电量为 q，球 2 的带电量为 nq，球 3 不带电且离球 1 和球 2 很远，此时球 1、2 之间作用力的大小为 F。现使球 3 先与球 2 接触，再与球 1 接触，然后 将球 3移至远处，此时 1、2 之间作用力的大小仍为 F，方向不变。由此可知 A..n=3 B..n=4 C..n=5 D.. n=6 69 解析：设 1、2 距离为 R，则： 2 2 nqF R  ，3与 2 接触后，它们带的电的电量均为： 2 nq ， 再 3 与 1 接触后，它们带的电的电量均为 ( 2) 4 n q ，最后 2 2 ( 2) 8 n n qF R   有上两式得： n=6 7（2011 新课标理综第 20 题）.一带负电荷的质点，在电场力作用下沿曲线 abc 从 a 运动到 c，已知质点的速率是递减的。关于 b 点电场强度 E 的方向，下列图示中可能正确的是（虚 线是曲线在 b 点的切线）（D） 解析：主要考查电场力方向和曲线运动所受合外力与轨迹的关系。正确答案是 D。 8（2011 天津第 5 题）．板间距为 d 的平行板电容器所带电荷量为 Q 时，两极板间的电势差 为 U1，板间场强为 E1。现将电容器所带电荷量变为 2Q，板间距变为 1 2 d，其他条件不变， 这时两极板间电势差为 U2，板间场强为 E2，下列说法正确的是 A．U2 = U1，E2 = E1 B．U2 = 2U1，E2 = 4E1 C．U2 = U1，E2 = 2E1 D．U2 = 2U1，E2 = 2E1 【解析】：考查平行板电容器的相关知识。 1 4 4 Q Q kdQU SC S kd        ， 1 1 4U kQE d S     ，当 电荷量变为 2Q 时， 2 1 2 2 4 2 Q Q kdQU USC S kd          ， 2 2 1 8 2 / 2 U kQE E d S      ，C 选项正确。 【答案】：C 9(广东第 21 题).图 8 为静电除尘器除尘机理的示意图。 尘埃在电场中通过某种机制带电，在电场力的作用下向集 尘极迁移并沉积，以达到除尘目的。下列表述正确的是 A.到达集尘极的尘埃带正电荷 B.电场方向由集尘极指向放电极 C.带电尘埃所受电场力的方向与电场方向相同 D.同一位置带电荷量越多的尘埃所受电场力越大 解析：电子吸附尘埃使尘埃带负电，受力与电场方向相反，AC 错。F=Eq，故 BD 正确。选 BD 10（2011 山东第 21 题）．如图所示，在两等量异种点电荷的电场中，MN 为两电荷连线的中 垂线，a、b、c三点所在直线平行于两电荷的连线，且 a 与 c 关于 MN 对称，b 点位于 MN 上， 70 d 点位于两电荷的连线上。以下判断正确的是 A．b 点场强大于 d 点场强 B．b 点场强小于 d 点场强 C．a、b 两点的电势差等于 b、c 两点间的电势差 D．试探电荷+q 在 a点的电势能小于在 c 点的电势能 答案：BC 解析：根据等量异种点电荷的电场的分布特点和叠加原理可知 A错误，B 正确；因为 a、b、 c三点所在直线平行于两电荷的连线，且 a与 c关于 MN 对称，a、b两点的电势差等于 b、c 两点间的电势差，C 正确；根据等量异种点电荷的电场的分布特点，a 点的电势高于 c 点的 电势，所以试探电荷+q 在 a 点的电势能大于在 c点的电势能，D 错误。 11(重庆第 19 题).如题 19 图所示，电量为+q 和-q 的点电荷分别位于正方体的顶点，正方体 范围内电场强度为零的点有 A. 体中心、各面中心和各边中点 B. 体中心和各边中点 C. 各面中心和各边中点 D. 体中心和各面中心 12（2011 上海第 1 题）．电场线分布如图昕示，电场中 a，b 两点的电场强度大小分别为已 知 aE 和 bE ，电势分别为 a 和 b ，则 (A) a bE E ， a b  (B) a bE E ， a b  (C) a bE E ， a b  (D) a bE E ， a b  答案：C 13（2011上海第14题）．两个等量异种点电荷位于x轴上，相对原点对称分布，正确描述电 势随位置 x变化规律的是图 答案：A 71 14 (2011上海第16题)．如图，在水平面上的箱子内，带异种电荷的小球a、b用绝缘细线分 别系于上、下两边，处于静止状态。地面受到的压力为 N ，球b所 受细线的拉力为 F 。剪断连接球b的细线后，在球b上升过程中地面 受到的压力 (A)小于 N (B)等于 N (C)等于 N F (D)大于 N F 答案：D 15 (2011上海23)．如图，在竖直向下，场强为 E的匀强电场中，长为 l的绝缘轻杆可绕固 定轴O在竖直面内无摩擦转动，两个小球A、B固定于杆的两端，A、 B的质量分别为 1m 和 2m ( 1 2m m )，A带负电，电量为 1q ，B带正 电，电量为 2q 。杆从静止开始由水平位置转到竖直位置，在此过程 中电场力做功为 ，在竖直位置处两球的总动能为 。 答案： 1 2( ) / 2q q El ， 1 2 2 1[( ) ( ) ] / 2q q E m m g l   16(浙江第 25 题).（22 分）如图甲所示，静电除尘装置中有一长为 L、宽为 b、高为 d的矩 形通道，其前、后面板使用绝缘材料，上、下面板使用金属材料。图乙是装置的截面图，上、 下两板与电压恒定的高压直流电源相连。质量为 m、电荷量为-q、分布均匀的尘埃以水平速 度 v0进入矩形通道，当带负电的尘埃碰到下板后其所带电荷被中和，同时被收集。通过调 整两板间距 d可以改变收集效率 。当 d=d0时为 81%（即离下板 0.81d0范围内的尘埃能够 被收集）。 不计尘埃的重力及尘埃之间的相互作用。 （1）求收集效率为 100%时，两板间距的最大值为 md ； （2）求收集率与两板间距 d 的函数关系； （3）若单位体积内的尘埃数为 n，求稳定工作时单位时间下板收集的尘埃质量 /M t  与 两板间距 d 的函数关系，并绘出图线。 答案：（1） 09.0 d （2）当 72 09.0 dd  时，收集效率 为 100%；当 09.0 dd  时，收集率 2 081.0       d d  （3） /M t  = d d nmbv 2 0 081.0 ，如图所示。 解析：（1）收集效率为 81%，即离下板 0.81d0的尘埃恰好到达下板的右端边缘，设高压电 源的电压为U ，在水平方向有 tvL 0 ① 在竖直方向有 2 0 2 181.0 atd  ② 其中 0md qU m qE m Fa  ③ 当减少两板间距是，能够增大电场强度，提高装置对尘埃的收集效率。收集效率恰好为 100% 时，两板间距为 md 。如果进一步减少 d ，收集效率仍为 100%。 因此，在水平方向有 tvL 0 ④ 在竖直方向有 2 2 1 tadm  ⑤ 其中 mmd qU m Eq m Fa      ⑥ 联立①②③④⑤⑥可得 09.0 ddm  ⑦ （2）通过前面的求解可知，当 09.0 dd  时，收集效率为 100% ⑧ 当 09.0 dd  时，设距下板 x处的尘埃恰好到达下板的右端边缘，此时有 2 02 1        v L md qUx ⑨ 根据题意，收集效率为 d x  ⑩ 联立①②③⑨⑩可得 2 081.0       d d  （3）稳定工作时单位时间下板收集的尘埃质量 /M t  = 0nmbdv 当 09.0 dd  时， 1 ，因此 /M t  = 0nmbdv 73 当 09.0 dd  时， 2 081.0       d d  ，因此 /M t  = d d nmbv 2 0 081.0 绘出的图线如下 17（2011北京第24题）．（20分） 静电场方向平行于x轴，其电势φ随x的分布可简化为如图所示的折线，图中φ0和d为已 知量。一个带负电的粒子在电场中以x=0为中心，沿x轴方向做周期性运动。已知该粒子质量 为m、电量为-q，其动能与电势能之和为－A（0m)的小物块同时轻放在斜面两侧的绸带上。两物块与绸带间的动摩擦因数相等，且最大 静摩擦力与滑动摩擦力大小相等。在α角取不同值的情况 下，下列说法正确的有 A．两物块所受摩擦力的大小总是相等 B．两物块不可能同时相对绸带静止 C．M不可能相对绸带发生滑动 D．m不可能相对斜面向上滑动 6（2011北京第18题）.“蹦极”就是跳跃者把一端 固定的长弹性绳绑在踝关节等处，从几十米高处跳 下的一种极限运动。某人做蹦极运动，所受绳子拉 力F的大小随时间t变化的情况如图所示。将蹦极过 程近似为在竖直方向的运动，重力加速度为g。据图 可知，此人在蹦极过程中最大加速度约为 A．G B．2g C．3g D．4g 7（2011上海第19题）．受水平外力F作用的物体，在粗糙水平面上作直线运动，其 v t 图 线如图所示，则 (A)在 10 t 秒内，外力F 大小不断增大 (B)在 1t 时刻，外力F 为零 (C)在 1 2t t 秒内，外力F 大小可能不断减小 (D)在 1 2t t 秒内，外力F 大小可能先减小后增大 答案：CD 8（2011上海第26题）.(5 分)如图，为测量作匀加速直线运动小车的加速度，将宽度均为b 的挡光片A、B固定在小车上，测得二者间距为d。 (1)当小车匀加速经过光电门时，测得两挡光片先后经过的时间 1t 和 2t ，则小车加速度 a  。 (2)(多选题)为减小实验误差，可采取的方法是( ) (A)增大两挡光片宽度b (B)减小两挡光片宽度b (C)增大两挡光片间距 d (D)减小两挡光片间距 d 答案． （1） 2 2 2 2 1 1 1[ ] 2 ( ) ( ) b d t t    (2)B，C 77 9（2011 天津第 19 题）（1）某同学用测力计研究在竖直方向运行的电梯运动状态。他在地 面上用测力计测量砝码的重力，示数为 G。他在电梯中用测力计仍测量同一砝码的重力， 发现测力计的示数小于 G，由此判断此时电梯的运动状态可能是减速上升或加速下降。 【解析】：物体处于失重状态，加速度方向向下，故而可能是减速上升或加速下降。 （2）用螺旋测微器测量某金属丝直径的结果如图所示。 该金属丝的直径是 1.706mm 【解析】：注意副尺一定要有估读。读数为 1.5+20.6× 0.01mm=1.706mm。因为个人情况不同，估读不一定一致， 本题读数 1.704-1.708 都算正确。 10.(浙江第 21 题)在“探究加速度与力、质量的关系”实验时，已提供了小车，一端附有定 滑轮的长木板、纸带、带小盘的细线、刻度尺、天平、导线。为了完成实验，还须从下图中 选取实验器材，其名称是 ① （漏选或全选得零分）；并分别写出所选器材的作用 ② 。 答案：①学生电源、电磁打点 计时器、钩码、砝码 或电火花计时器、钩码、砝码 ②学生电源为电磁打点计时器 提供交流电源；电磁打点计时 器（电火花计时器）记录小车 运动的位置和时间；钩码用以 改变小车的质量；砝码用以改 变小车受到的拉力的大小，还可以用于测量小车的质量。 解析：电磁打点计时器（电火花计时器）记录小车运动的位置和时间；钩码用以改变小车的 质量；砝码用以改变小车受到的拉力的大小，还可以用于测量小车的质量。如果选电磁打点 计时器，则需要学生电源，如果选电火花计时器，则不需要学生电源。 11(新课标理综第 23 题).（10 分） 利用图 1 所示的装置可测量滑块在斜面上运动的加速度。一斜面上安装有两个光电门， 其中光电门乙固定在斜面上靠近底端处，光电门甲的位置可移动，当一带有遮光片的滑块自 斜面上滑下时，与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间 78 t。改变光电门甲的位置进行多次测量，每次都使滑块从同一点由静止开始下滑，并用米尺 测量甲、乙之间的距离 s，记下相应的 t 值；所得数据如下表所示。 s（m） 0.500 0.600 0.700 0.800 0.900 0.950 t(ms) 292.9 371.5 452.3 552.8 673.8 776.4 s/t(m/s) 1.71 1.62 1.55 1.45 1.34 1.22 完成下列填空和作图： （1）若滑块所受摩擦力为一常量，滑块加速度的大小 a、滑块经过光电门乙时的瞬时速度 v1测量值 s和 t四个物理量之间所满足的关系式是_______； (2)根据表中给出的数据，在图 2给出的坐标纸上 画出 图线； （3）由所画出的 图线，得出滑块加速度的大 小为 a=____________m/s 2 （保留 2位有效数字）。 解析：（1）滑块做匀加速直线运动，利用 atvvvv t  0 2 和 有 21 ta t sv  解 得 tvatsvat t s 1 2 1 2 1 2 1  或 （2） 图线如图所示t t s  （3）由 12 1 vat t s  可知， 图线t t s  斜率 绝对值为 2 1 a即 2 2 1  ak ，解得 a=2 79 12(重庆第 22（2）题)某同学设计了如题 22 图 3 所示的装置，利用米尺、秒表、轻绳、轻 滑轮、轨道、滑块、托盘和砝码等器材来制定 滑块和轨道间的动摩擦因数μ。滑块和托盘上 分别放有若干砝码，滑块质量为 M，滑块上砝码总质量为 m‘，托盘和盘中砝码的总质量为 m， 实验中，滑块在水平轨道上从 A 到 B 做 初速为零的匀加速直线运动，重力加速 度 g 取 10m／s2。 ①为测量滑块的加速度a，须测出它在 A、B 间运动的 与 ，计 算a的运动学公式是 ； ②根据牛顿运动定律得到 a与m 的关 系为：     1 g a m g M m m        他想通过多次改变m，测出相应的a值，并利用上式来计算 。若要求a是m的一次函数， 必须使上式中的 保持不变，实验中应将从托盘中取出的砝码置 于 ； ③实验得到 a与m的关系如题 22 图 4 所示，由此可知μ= （取两位有效数字） 答案 ：①位移 时间 ②m′+m 滑块上 ③ =0.23(0.21—0 25) 13(上海第31题)．(12 分)如图，质量 2m kg 的物体静止于水平地面的A处，A、B间距L=20m。 用大小为30N，沿水平方向的外力拉此物体，经 0 2t s 拉至B处。(已知 cos37 0.8  ， sin 37 0.6  。取 210 /g m s ) (1)求物体与地面间的动摩擦因数μ； (2)用大小为30N，与水平方向成37°的力斜向 80 上拉此物体，使物体从A处由静止开始运动并能到达B处，求该力作用的最短时间t。 答案．(12 分) (1)物体做匀加速运动 2 0 1 2 L at (1 分) ∴ 2 2 2 0 2 2 20 10( / ) 2 La m s t     （1分） 由牛顿第二定律 F f ma  （1分） 30 2 10 10( )f N    (1 分) ∴ 10 0.5 2 10 f mg      (1 分) (2)设 F 作用的最短时间为 t，小车先以大小为 a的加速度匀加速 t秒，撤去外力后， 以大小为 'a ，的加速度匀减速 't 秒到达 B 处，速度恰为 0，由牛顿定律 cos37 ( sin 37 )F mg F a ma    (1 分) ∴ 2(cos37 sin 37 ) 30 (0.8 0.5 0.6) 0.5 10 11.5( / ) 2 Fa g m s m             (1 分) 2' 5( / )fa g m s m    （1分） 由于匀加速阶段的末速度即为匀减速阶段的初速度，因此有 ' 'at a t （1分） ∴ 11.5' 2.3 ' 5 at t t t a    （1 分） 2 21 1 ' ' 2 2 L at a t  （1分） ∴ 2 2 2 2 20 1.03( ) 2.3 ' 11.5 2.3 5 Lt s a a        （1分） （2）另解：设力F 作用的最短时间为 t，相应的位移为 s，物体到达 B 处速度恰为 0，由动 能定理 [ cos37 ( sin 37 )] ( ) 0F mg F s mg L s       （2分） ∴ 0.5 2 10 20 6.06( ) (cos37 sin 37 ) 30 (0.8 0.5 0.6) mgLs m F              （1分） 由牛顿定律 cos37 ( sin 37 )F mg F ma    （1分） 81 ∴ 2(cos37 sin 37 ) 30 (0.8 0.5 0.6) 0.5 10 11.5( / ) 2 Fa g m s m             （1 分） ∵ 21 2 s at （1 分） 2 2 6.06 1.03( ) 11.5 st s a     （1分） 2011 普通高校招生考试试题汇编-曲线运动 1 (2011 江苏卷第 3 题)．如图所示，甲、乙两同学从河中 O 点出发，分别沿直线游到 A 点 和 B 点后，立即沿原路线返回到 O 点，OA、OB 分别与水 流方向平行和垂直，且 OA＝OB。若水流速度不变，两人 在靜水中游速相等，则他们所用时间 t 甲、t 乙的大小关 系为 A．t 甲＜t 乙 B．t 甲＝t 乙 C．t 甲＞t 乙 D．无法确定 2（2011 广东第 17 题）.如图 6 所示，在网球的网前截击练习中，若练习者在球网正上方距 地面 H处，将球以速度 v 沿垂直球网的方向击出，球刚好落在底线上，已知底线到网的距离 为 L，重力加速度取 g，将球的运动视作平抛运动，下列表述正确的是 A.球的速度 v 等于 L 2H g B.球从击出至落地所用时间为 2H g C.球从击球点至落地点的位移等于 L D.球从击球点至落地点的位移与球的质量有关 解析：由平抛运动规律：L=vt，H= 2 1 gt 2 求出 AB 正确。选 AB A.球的速度 v 等于 2 gL H B.球从击出至落地所用时间为 2H g C.球从击球点至落地点的位移等于 L D.球从击球点至落地点的位移与球的质 量有关 3（2011 安徽第 17 题）．一般的曲线运动可以 ρ A v0 α ρ P 图（a） 图（b） 82 分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小 圆弧来代替。如图（a）所示，曲线上的 A 点的曲率圆定义为：通过 A 点和曲线上紧邻 A 点 两侧的两点作一圆，在极限情况下，这个圆就叫做 A点的曲率圆，其半径ρ叫做 A点的曲率 半径。现将一物体沿与水平面成α角的方向已速度υ0抛出，如图（b）所示。则在其轨迹最 高点 P处的曲率半径是 A． 2 0v g B． 2 2 0 sinv g  C． 2 2 0 cosv g  D． 2 2 0 cos sin v g   答案：C 解析：物体在其轨迹最高点 P处只有水平速度，其水平速度大小为 v0cosα，根据牛顿第二 定律得 2 0( cos )vmg m    ，所以在其轨迹最高点 P 处的曲率半径是 2 2 0 cosv g    ，C 正 确。 4（2011 全国理综第 20 题）.一带负电荷的质点，在电场力作用下沿曲线 abc 从 a 运动到 c， 已知质点的速率是递减的。关于 b 点电场强度 E的方向，下列图示中可能正确的是（虚线是 曲线在 b 点的切线）（D） 解析：主要考查电场力方向和曲线运动所受合外力与轨迹的关系。正确答案是 D。 5（2011上海第11题）．如图，人沿平直的河岸以速度 v行走，且通过不可伸长的绳拖船， 船沿绳的方向行进，此过程中绳始终与水面平行。当绳与河岸的夹角为 ，船的速率为 (A) sinv  (B) sin v  (C) cosv  (D) cos v  答案：C 6（2011上海第25题）．以初速为 0v ，射程为 s的平抛运动轨迹制成一光滑轨道。一物体由 静止开始从轨道顶端滑下，当其到达轨道底部时，物体的速率为 ，其水平方向 的速度大小为 。 答案. 0/gs v ， 2 2 0 0/ 1 ( / )v v gs 7（2011 海南第 15 题）。如图，水平地面上有一个坑，其竖直截面为半圆。ab 为沿水平方向 83 的直径。若在 a 点以初速度 0v 沿 ab 方向抛出一小球， 小球会击中坑壁上的 c 点。已知 c 点与水平地面的距离为圆半径的一半，求圆的半径。 解析：设圆半径为 r，质点做平抛运动，则： 0x v t ① 210.5 2 y r gt  ② 过 c 点做 cd⊥ab 与 d 点，Rt△acd∽Rt△cbd 可得 2cd ad db  即为： 2( ) (2 ) 2 r x r x  ③ 由①②③得： 2 0 4(7 4 3)r v g   8（2011 天津第 10 题）．（16 分） 如图所示，圆管构成的半圆形竖直轨道固定在水平地面上，轨道半径为 R，MN 为直径且与水 平面垂直，直径略小于圆管内径的小球 A 以某一初速度冲进轨道，到达半圆轨道最高点 M 时与静止于该处的质量与 A 相同的小 球 B 发生碰撞，碰后两球粘在一起飞 出轨道，落地点距 N 为 2R。重力加速 度为 g，忽略圆管内径，空气阻力及各 处摩擦均不计，求： （1）粘合后的两球从飞出轨道到落地 的时间 t； （2）小球 A 冲进轨道时速度 v 的大小。 解析： （1）粘合后的两球飞出轨道后做平抛运动，竖直方向分运动为自由落体运动，有 212 2 R gt ① 解得 2 Rt g  ② （2）设球 A 的质量为 m，碰撞前速度大小为 v1，把球 A冲进轨道最低点时的重力势能定为 0， 由机械能守恒定律知 2 2 1 1 1 2 2 2 mv mv mgR  ③ 84 设碰撞后粘合在一起的两球速度大小为 v2，由动量守恒定律知 1 22mv mv ④ 飞出轨道后做平抛运动，水平方向分运动为匀速直线运动，有 22R v t ⑤ 综合②③④⑤式得 2 2 2v gR 9（2011 山东第 24 题）.（15 分）如图所示，在高出水平地面 1.8h m 的光滑平台上放置 一质量 2M kg 、由两种不同材料连接成一体的薄板 A，其右段长度 1 0.2l m 且表面光滑， 左段表面粗糙。在 A最右端放有可视为质点的物块 B，其质量 1m kg 。B与 A左段间动摩 擦因数 0.4u  。开始时二者均静止，先对 A施加 20F N 水平向右的恒力，待 B 脱离 A（A 尚未露出平台）后，将 A取走。B离开平台后的落地点与平台右边缘的水平距离 1.2x m 。 （取 210mg s ）求： （1）B离开平台时的速度 Bv 。 （2）B从开始运动到刚脱离 A时，B 运动的时间 ts和位移 xB （3）A左端的长度 l2 解析： 85 10（2011 广东第 36 题）、（18 分）如图 20 所示，以 A、B 和 C、D 为端点的两半圆形光滑轨 道固定于竖直平面内，一滑板静止在光滑水平地面上，左端紧靠 B 点，上表面所在平面与两 半圆分别相切于 B、C。一物块被轻放在水平匀速运动的传送带上 E 点，运动到 A 时刚好与 传送带速度相同，然后经 A 沿半圆轨道滑下，再经 B 滑上滑板。滑板运动到 C 时被牢固粘连。 物块可视为质点，质量为 m，滑板质量 M=2m，两半圆半径均为 R，板长 l =6.5R，板右端到 C 的距离 L 在 R＜L＜5R 范围内取值。E 距 A 为 S=5R，物块与传送带、物块与滑板间的动摩 擦因素均为μ=0.5，重力加速度取 g. (3)求物块滑到 B 点的速度大小； (4)试讨论物块从滑上滑板到离开滑板右端的过程中，克服摩擦力做的功 Wf与 L的关系，并 判断物块能否滑到 CD 轨道的中点。 解析： （1）μmgs+mg·2R= 2 1 mvB 2 ① 所以 vB=3 Rg （2）设 M 滑动 x1,m 滑动 x2二者达到共同速度 v,则 mvB=(M+m)v ② μmgx1= 2 1 mv 2 ③ —μmgx2= 2 1 mv2— 2 1 mvB 2 ④ 由②③④得 v= Rg , x1=2R, x2=8R 二者位移之差△x= x2—x1=6R＜6.5R，即滑块未掉下滑板 讨论： 1 R＜L＜2R 时，Wf=μmg(l+L)= 2 1 mg（6.5R+L） 86 2 2R≤L＜5R 时，Wf=μmgx2+μmg(l—△x)=4.25mgR＜4.5mgR，即滑块速度不为 0，滑上 右侧轨道。 要使滑块滑到 CD 轨道中点，vc必须满足： 2 1 mvc 2 ≥mgR ⑤ 此时 L应满足：μmg(l+L) ≤ 2 1 mvB 2 — 2 1 mvc 2 ⑥ 则 L≤ 2 1 R，不符合题意，滑块不能滑到 CD 轨道中点。 答案：（1） vB=3 Rg （2） ①R＜L＜2R 时，Wf=μmg(l+L)= 2 1 mg（6.5R+L） ②2R≤L＜5R 时，Wf=μmgx2+μmg(l—△x)=4.25mgR＜4.5mgR，即滑块速度不为 0，滑上右 侧轨道。 滑块不能滑到 CD 轨道中点 2011 普通高校招生考试试题汇编-万有引力定律 1 (2011 江苏第 7题)．一行星绕恒星作圆周运动。由天文观测可得，其运动周期为 T，速度 为 v，引力常量为 G，则 A．恒星的质量为 3 2 v T G B．行星的质量为 2 3 2 4 v GT  C．行星运动的轨道半径为 2 vT  D．行星运动的加速度为 2 v T  2（2011 山东第 17 题）.甲、乙为两颗地球卫星，其中甲为地球同步卫星，乙的运行高度低 于甲的运行高度，两卫星轨道均可视为圆轨道。以下判断正确的是 A.甲的周期大于乙的周期 B.乙的速度大于第一宇宙速度 C.甲的加速度小于乙的加速度 D.甲在运行时能经过北极的正上方 答案：AC 解析：万有引力提供向心力，由 2 22 2 4 T mr r vmma r MmG   ，可得向心加速度之比 87 12 2  甲 乙 乙 甲 r r a a ，C 正确；周期之比 13 3  乙 甲 乙 甲 r r T T ，A正确；甲、乙均为两颗地球卫星，运 行速度都小于第一宇宙速度，B 错误；甲为地球同步卫星运行在赤道上方，D 错误。 3(广东第 20 题).已知地球质量为 M，半径为 R，自转周期为 T，地球同步卫星质量为 m，引 力为 G。有关同步卫星，下列表述正确的是 A.卫星距离地面的高度为 23 24 GMT  B.卫星的运行速度小于第一宇宙速度 C.卫星运行时受到的向心力大小为 2 MmG R D.卫星运行的向心加速度小于地球表面的重力加速度 4（2011 全国卷 1第 19 题）．我国“嫦娥一号”探月卫星发射后，先在“24 小时轨道”上绕 地球运行(即绕地球一圈需要24小时)；然后，经过两次变轨依次到达“48小时轨道”和“72 小时轨道”；最后奔向月球。如果按圆形轨道计算，并忽略卫星质量的变化，则在每次变轨 完成后与变轨前相比， A．卫星动能增大，引力势能减小 B．卫星动能增大，引力势能增大 C．卫星动能减小，引力势能减小 D．卫星动能减小，引力势能增大 解析：周期变长，表明轨道半径变大，速度减小，动能减小,引力做负功故引力势能增大 选 D 5（2011 全国理综新课标 19）.卫星电话信号需要通地球同步卫星传送。如果你与同学在地 面上用卫星电话通话，则从你发出信号至对方接收到信号所需最短时间最接近于（可能用到 的数据：月球绕地球运动的轨道半径约为 3.8×10 5 m/s，运行周期约为 27 天，地球半径约为 6400 千米，无线电信号传播速度为 3x10 8 m/s）（B） A.0.1s B.0.25s C.0.5s D.1s 解析：主要考查开普勒第三定律。月球、地球同步卫星绕地球做匀速圆周运动，根据开普勒 第 三 定 律 有 2 1 2 2 3 3 2 1 T T r r  解 得 3 2 1 2 2 12 T T rr  ， 代 入 数 据 求 得 7 2 102.4 r m.如图所示，发出信号至对方接收到信号所需最短时间 为 C rR v st 2 2 22   ，代入数据求得 t=0.28s.所以正确答案是 B。 6（2011 天津第 8题）． 质量为 m的探月航天器在接近月球表面的轨道上飞行，其运动视为 匀速圆周运动。已知月球质量为 M，月球半径为 R，月球表面重力加速度为 g，引力常量 为 G，不考虑月球自转的影响，则航天器的 A．线速度 GMv R  B．角速度 gR  88 C．运行周期 2 RT g  D．向心加速度 2 GMa R  【解析】：万有引力提供卫星做圆周运动的向心力，代入相关公式即可 【答案】：AC 7（2011 浙江第 19 题）.为了探测 X星球，载着登陆舱的探测飞船在该星球中心为圆心，半 径为 r1的圆轨道上运动，周期为 T1，总质量为 m1。随后登陆舱脱离飞船，变轨到离星球更 近的半径为 r2 的圆轨道上运动，此时登陆舱的质量为 m2则 A. X 星球的质量为 2 1 1 24 GT rM   B. X 星球表面的重力加速度为 2 1 1 24 T rg X   C. 登陆舱在 1r 与 2r 轨道上运动是的速度大小之比为 12 21 2 1 rm rm v v  D. 登陆舱在半径为 2r 轨道上做圆周运动的周期为 3 1 3 2 12 r r TT  答案：AD 解 析 ： 根 据 2 1 112 1 1 2M        T rm r mG  、 2 2 222 2 2 2M        T rm r mG  ， 可 得 2 1 1 24 GT rM   、 3 1 3 2 12 r r TT  ，故 A、D 正确；登陆舱在半径为 1r 的圆轨道上运动的向心加速度 2 1 1 2 2 11 4 T rra    ，此加速度与 X 星球表面的重力加速度并不相等，故 C 错误；根据 r vm r m 2 2 GM  ，得 r GMv  ，则 1 2 2 1 r r v v  ，故 C 错误。 8 (2011 广东第 20 题).已知地球质量为 M，半径为 R，自转周期为 T，地球同步卫星质量为 m，引力常量为 G。有关同步卫星，下列表述正确的是 A.卫星距离地面的高度为 23 24 GMT  B.卫星的运行速度小于第一宇宙速度 C.卫星运行时受到的向心力大小为 2 MmG R 89 D.卫星运行的向心加速度小于地球表面的重力加速度 解析：根据 )()2( )( 2 2 HR T m HR MmG    ，A 错，由 HR vm HR MmG    2 2)( ，B 正确， 由 mg HR MmG   2)( ，C错 D对。选 BD 9 (2011北京第15题)．由于通讯和广播等方面的需要，许多国家发射了地球同步轨道卫星， 这些卫星的 A．质量可以不同 B．轨道半径可以不同 C．轨道平面可以不同 D．速率可以不同 10(重庆第 21 题).某行星和地球绕太阳公转的轨道均可视为圆。每过 N年，该行星会运行到日地连线的延长线上，如题 21 图所示。该行星 与地球的公转半径比为 A． 2 31( )N N  B. 2 3( ) 1 N N  C． 3 21( )N N  D. 3 2( ) 1 N N  11（2011 海南第 12 题）.2011 年 4 月 10 日，我国成功发射第 8颗北斗导航卫星，建成以后 北斗导航卫星系统将包含多可地球同步卫星，这有助于减少我国对 GPS 导航系统的依赖，GPS 由运行周期为 12 小时的卫星群组成，设北斗星的同步卫星和 GPS 导航的轨道半径分别为 1R 和 2R ，向心加速度分别为 1a 和 2a ，则 1 2:R R =_____。 1 2:a a =_____（可用根式表示） 答案 ： 3 4 、 3 2 4 解 析 ： 1 2 2T T  ， 由 2 2 2 4GMm m R ma R T    得 ： 2 3 24 GMTR   ， 2 GMa R  因 而 ： 2 3 31 1 2 2 4R T R T        ， 2 3 1 1 2 2 2 4 a R a R         12（2011上海22B）．人造地球卫星在运行过程中由于受到微小的阻力，轨道半径将缓慢减 小。在此运动过程中，卫星所受万有引力大小将 (填“减小”或“增大”)；其 动能将 (填“减小”或“增大”)。 答案：增大，增大 90 13（2011 安徽第 22 题）．（14 分） （1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴 a的三次方与它 的公转周期 T 的二次方成正比，即 3 2 a k T  ，k 是一个对所有行星都相同的常量。将行星绕 太阳的运动按圆周运动处理，请你推导出太阳系中该常量 k的表达式。已知引力常量为 G， 太阳的质量为 M 太。 （2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都 成立。经测定月地距离为 3.84×10 8 m，月球绕地球运动的周期为 2.36×10 6 S，试计算地球的 质 M 地。（G=6.67×10 -11 Nm 2 /kg 2 ，结果保留一位有效数字） 解析：（1）因行星绕太阳作匀速圆周运动，于是轨道的半长轴 a 即为轨道半径 r。根据万有 引力定律和牛顿第二定律有 2 2 2( ) m M G m r r T  行 太 行 ① 于是有 3 2 24 r G M T   太 ② 即 24 Gk M   太 ③ （2）在月地系统中，设月球绕地球运动的轨道半径为 R，周期为 T，由②式可得 3 2 24 R G M T   地 ④ 解得 M 地=6×10 24 kg ⑤ （M 地=5×10 24 kg 也算对） 2011 普通高校招生考试试题汇编-直线运动 1（2011 安徽第 16 题）．一物体作匀加速直线运动，通过一段位移 x 所用的时间为 1t ，紧 接着通过下一段位移 x 所用时间为 2t 。则物体运动的加速度为 A． 1 2 1 2 1 2 2 ( ) ( ) x t t t t t t    B． 1 2 1 2 1 2 ( ) ( ) x t t t t t t    C． 1 2 1 2 1 2 2 ( ) ( ) x t t t t t t    D． 1 2 1 2 1 2 ( ) ( ) x t t t t t t    答案：A 解析：物体作匀加速直线运动在前一段 x 所用的时间为 1t ，平均速度为 1 1 xv t   ，即为 1 2 t 时 刻的瞬时速度；物体在后一段 x 所用的时间为 2t ，平均速度为 2 2 xv t   ，即为 2 2 t 时刻的瞬 91 时速度。速度由 1v 变化到 2v 的时间为 1 2 2 t tt    ，所以加速度 2 1 1 2 1 2 1 2 2 ( ) ( ) v v x t ta t t t t t        ， A正确。 2(2011 海南第 8题）.一物体自 t=0 时开始做直线运动，其速度图线如图所示。下列选项正 确的是 A.在 0～6s 内，物体离出发点最远为 30m B.在 0～6s 内，物体经过的路程为 40m[ C.在 0～4s 内，物体的平均速率为 7.5m/s D. 5～6s 内，物体所受的合外力做负功 解析：A，0—5s,物体向正向运动，5—6s 向 负向运动，故 5s 末离出发点最远，A 错 B 由面积法求出 0—5s 的位移 s1=35m, 5—6s 的位移 s2=-5m,总路程为：40m,B 对 C 由面积法求出 0—4s 的位移 s=30m，平度速度为：v=s/t=7.5m/s C 对 D 由图像知 5～6s 过程物体加速，合力和位移同向，合力做正功，D 错 3（2011 新课标理综第 15 题）.一质点开始时做匀速直线运动，从某时刻起受到一恒力作用。 此后，该质点的动能可能（ABD） A. 一直增大 B. 先逐渐减小至零，再逐渐增大 C. 先逐渐增大至某一最大值，再逐渐减小 D. 先逐渐减小至某一非零的最小值，再逐渐增大 解析：主要考查力和运动关系。当恒力方向与速度在一条直线上，质点的动能可能一直增大， 也可能先逐渐减小至零，再逐渐增大。当恒力方向与速度不在一条直线上，质点的动能可能 一直增大，也可能先逐渐减小至某一非零的最小值，再逐渐增大。所以正确答案是 ABD。 4（2011 天津第 3 题）．质点做直线运动的位移 x 与时间 t 的关系为 x = 5t + t2 （各物理 量均采用国际单位制单位），则该质点 A．第 1s 内的位移是 5m B．前 2s 内的平均速度是 6m/s C．任意相邻 1s 内的位移差都是 1m D．任意 1s 内的速度增量都是 2m/s 【解析】：匀变速直线运动的考查，简单题。第 1s 内的位移只需将 t=1 代入即可求出 x=6m， A 错误；前 2s 内的平均速度为 2 2 5 2 2 7m/s 2 2 sv      ，B 错；由题给解析式可以求得 加速度为 a=2m/s2 2 2mx aT   ，C错；由加速的定义可知 D 选项正确 【答案】：D 5（2011 广东第 34 题）、（18 分） （1）图 14 是“研究匀变数直线运动”实验中获得的一 条纸带，O、A、B、C、D 和 E为纸带上六个计数点。加 速度大小用 a 表示 0 A B C D E 1 cm 2 3 92 ①OD 间的距离为 cm ②图 15 是根据实验数据绘出的 s—t2 图线（s 为各计数点至同一起点的距离），斜率表 示 ，其大小为 m/s2(保留三位有效数字)。 解析：（1）答案：1.20 a/2 0.933 1 要估读一位，②s=v0t+ 2 1 at 2 ，斜率为 a/2 6（2011 山东第 23 题）.（12 分） （1）某探究小组设计了“用一把尺子测定动摩擦因数”的 实验方案。如图所示，将一个小球和一个滑块用细绳连接， 跨在斜面上端。开始时小球和滑块均静止，剪短细绳后， 小球自由下落，滑块沿斜面下滑，可先后听到小球落地和 滑块撞击挡板的声音，保持小球和滑块释放的位置不变， 调整挡板位置，重复以上操作，直到能同时听到小球落地 和滑块撞击挡板的声音。用刻度尺测出小球下落的高度 H、 滑块释放点与挡板处的高度差 h 和沿斜面运动的位移 x。（空气阻力对本实验的影响可以忽 略） ①滑块沿斜面运动的加速度与重力加速度的比值为________。 ②滑块与斜面间的动摩擦因数为__________________。 ③以下能引起实验误差的是________。 a．滑块的质量 b．当地重力加速度的大小 c．长度测量时的读数误差 93 d．小球落地和滑块撞击挡板不同时 答案：① H x ② 22 2 1)( hxH xh   ③c d 7 (2011 重庆第 14 题).某人估测一竖直枯井深度，从井口静止释放一石头并开始计时，经 2s 听到石头落地声，由此可知井深约为（不计声音传播时间，重力加速度 g取 10m/s2） A.10m B. 20m C. 30m D. 40m 〖解析〗〖答案〗B. mmgth 20210 2 1 2 1 22  ，由此可知井深约为 20m 8 (上海第19题)．受水平外力F作用的物体，在粗糙水平面上作直线运动，其 v t 图线如 图所示，则 (A)在 10 t 秒内，外力F 大小不断增大 (B)在 1t 时刻，外力F 为零 (C)在 1 2t t 秒内，外力F 大小可能不断减小 (D)在 1 2t t 秒内，外力F 大小可能先减小后增大 9(上海第26题).如图，为测量作匀加速直线运动小车的加速度，将宽度 均为b的挡光片A、B固定在小车上，测得二者间距为d。 (1)当小车匀加速经过光电门时，测得两挡光片先后经过的时间 1t 和 2t ，则小车加速度 a  。 (2)(多选题)为减小实验误差，可采取的方法是( ) (A)增大两挡光片宽度b (B)减小两挡光片宽度b (C)增大两挡光片间距 d (D)减小两挡光片间距 d 答案：（1） 2 2 2 2 1 1 1[ ] 2 ( ) ( ) b d t t    (2)B，C 10(新课标理综第 21 题).如图，在光滑水平面上有一质量为 m1的足够长的木板，其上叠放 一质量为 m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施 加一随时间 t增大的水平力 F=kt（k 是常数），木板和木块加速度的大小分别为 a1和 a2，下 列反映 a1和 a2变化的图线中正确的是 94 答案：B。 解析：当 2 1 2 1 ( )mF g m m m   时：木板和木块一起运动 1 2 1 2 kta a m m    满足：木板和木块间的摩擦力 2f m g 合题意 当 2 1 2 1 ( )mF g m m m   时：木块在木板上滑动 2 2 1 2 1 2 ,m g F m ga a m m     满足：a2>a1合题意 11(新课标理综第 23). 利用图 1 所示的装置可测量滑块在斜面上运动的加速度。一斜面上安装有两个光电门， 其中光电门乙固定在斜面上靠近底端处，光电门甲的位置可移动，当一带有遮光片的滑块自 斜面上滑下时，与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间 t。改变光电门甲的位置进行多次测量，每次都使滑块从同一点由静止开始下滑，并用米尺 测量甲、乙之间的距离 s，记下相应的 t 值；所得数据如下表所示。 s（m） 0.500 0.600 0.700 0.800 0.900 0.950 t(ms) 292.9 371.5 452.3 552.8 673.8 776.4 s/t(m/s) 1.71 1.62 1.55 1.45 1.34 1.22 完成下列填空和作图： （1）若滑块所受摩擦力为一常量，滑块加速度的 大小 a、滑块经过光电门乙时的瞬时速度 v1测量值 s和t四个物理量之间所满足的关系式是_______； (2)根据表中给出的数据，在图 2给出的坐标纸上 95 画出 图线； （3）由所画出的 图线，得出滑块加速度的大小为 a=____________m/s 2 （保留 2 位有效 数字）。 解析：（1）滑块做匀加速直线运动，利用 atvvvv t  0 2 和 有 21 ta t sv  解得 tvatsvat t s 1 2 1 2 1 2 1  或 （2） 图线如图所示t t s  （3）由 12 1 vat t s  可知， 图线t t s  斜率 绝对值为 2 1 a即 2 2 1  ak ，解得 a=2 12(新课标理综第 24 题).（13 分） 甲乙两辆汽车都从静止出发做加速直线运动，加速度方向一直不变。在第一段时间间隔内， 两辆汽车的加速度大小不变，汽车乙的加速度大小是甲的两倍；在接下来的相同时间间隔内， 汽车甲的加速度大小增加为原来的两倍，汽车乙的加速度大小减小为原来的一半。求甲乙两 车各自在这两段时间间隔内走过的总路程之比。 解析：设汽车甲在第一段时间间隔末（时间 t0）的速度为 v ,第一段时间间隔内行驶的路程 为 s1, 加 速 度 为 a , 在 第 二 段 时 间 间 隔 内 行 驶 的 路 程 为 s2 。 由 运 动 学 公 式 得 0atv  ① 2 01 2 1 ats  ② 2 002 )2( 2 1 tavts  ③ 设乙车在时间 t0的速度为 v，在第一、二段时间间隔内行驶的路程分别为  1s 、  2s 。同样 有 0)2( tav  ④ 2 01 )2( 2 1 tas  ⑤ 2 002 2 1 attvs  ⑥ 设甲、乙两车行驶的总路程分别为 s、 s，则有 21 sss  ⑦  21 sss ⑧ 联立以上各式解得，甲、乙两车各自行驶的总路程之比为 7 5  s s ⑨ 13（2011 四川第 23 题）．（16 分） 随着机动车数量的增加，交通安全问题日益凸显。分析交通违法事例，将警示我们遵守 交通法规，珍惜生命。一货车严重超载后的总质量为 49t，以 54km/h 的速率匀速行驶。发 96 现红灯时司机刹车，货车即做匀减速直线运动，加速度的大小为 2.5m/s 2 （不超载时则为 5m/s 2 ）。 （1）若前方无阻挡，问从刹车到停下来此货车在超载及不超载时分别前进多远？ （2）若超载货车刹车时正前方 25m 处停着总质量为 1t 的轿车，两车将发生碰撞，设相 互作用 0.1 s 后获得相同速度，问货车对轿车的平均冲力多大？ 【解析】（1）货车刹车时的初速是 v0=15vm/s ，末速是 0，加速度分别是 2.5m/s 2 和 5m/s 2 ， 根据位移推论式得 a v S 2 2 0 代入数据解得： 超载 45S m 不超载 5.22S m （2）货车与轿车相撞时的速度为 10255.2222522 0  aSvv m/s 相撞时动量守恒，有 VmMMv )(  得 8.9V m/s 对轿车根据动量定理有 mVft  解得 4108.9 f N 14(上海第31题)．(12 分)如图，质量 2m kg 的物体静止于水平地面的A处，A、B间距L=20m。 用大小为30N，沿水平方向的外力拉此物体，经 0 2t s 拉至B处。(已知 cos37 0.8  ， sin 37 0.6  。取 210 /g m s ) (1)求物体与地面间的动摩擦因数μ； (2)用大小为30N，与水平方向成37°的力斜 向上拉此物体，使物体从A处由静止开始运 动并能到达B处，求该力作用的最短时间t。 解析：答案．(12 分) (1)物体做匀加速运动 2 0 1 2 L at (1 分) ∴ 2 2 2 0 2 2 20 10( / ) 2 La m s t     （1分） 由牛顿第二定律 F f ma  （1分） 30 2 10 10( )f N    (1 分) ∴ 10 0.5 2 10 f mg      (1 分) 97 (2)设 F 作用的最短时间为 t，小车先以大小为 a的加速度匀加速 t秒，撤去外力后， 以大小为 'a ，的加速度匀减速 't 秒到达 B 处，速度恰为 0，由牛顿定律 cos37 ( sin 37 )F mg F a ma    (1 分) ∴ 2(cos37 sin 37 ) 30 (0.8 0.5 0.6) 0.5 10 11.5( / ) 2 Fa g m s m             (1 分) 2' 5( / )fa g m s m    （1分） 由于匀加速阶段的末速度即为匀减速阶段的初速度，因此有 ' 'at a t （1分） ∴ 11.5' 2.3 ' 5 at t t t a    （1 分） 2 21 1 ' ' 2 2 L at a t  （1分） ∴ 2 2 2 2 20 1.03( ) 2.3 ' 11.5 2.3 5 Lt s a a        （1分） （2）另解：设力F 作用的最短时间为 t，相应的位移为 s，物体到达 B 处速度恰为 0，由动 能定理 [ cos37 ( sin 37 )] ( ) 0F mg F s mg L s       （2分） ∴ 0.5 2 10 20 6.06( ) (cos37 sin 37 ) 30 (0.8 0.5 0.6) mgLs m F              （1分） 由牛顿定律 cos37 ( sin 37 )F mg F ma    （1分） ∴ 2(cos37 sin 37 ) 30 (0.8 0.5 0.6) 0.5 10 11.5( / ) 2 Fa g m s m             （1 分） ∵ 21 2 s at （1 分） 2 2 6.06 1.03( ) 11.5 st s a     （1分）