高考数学汇编解析几何 24页

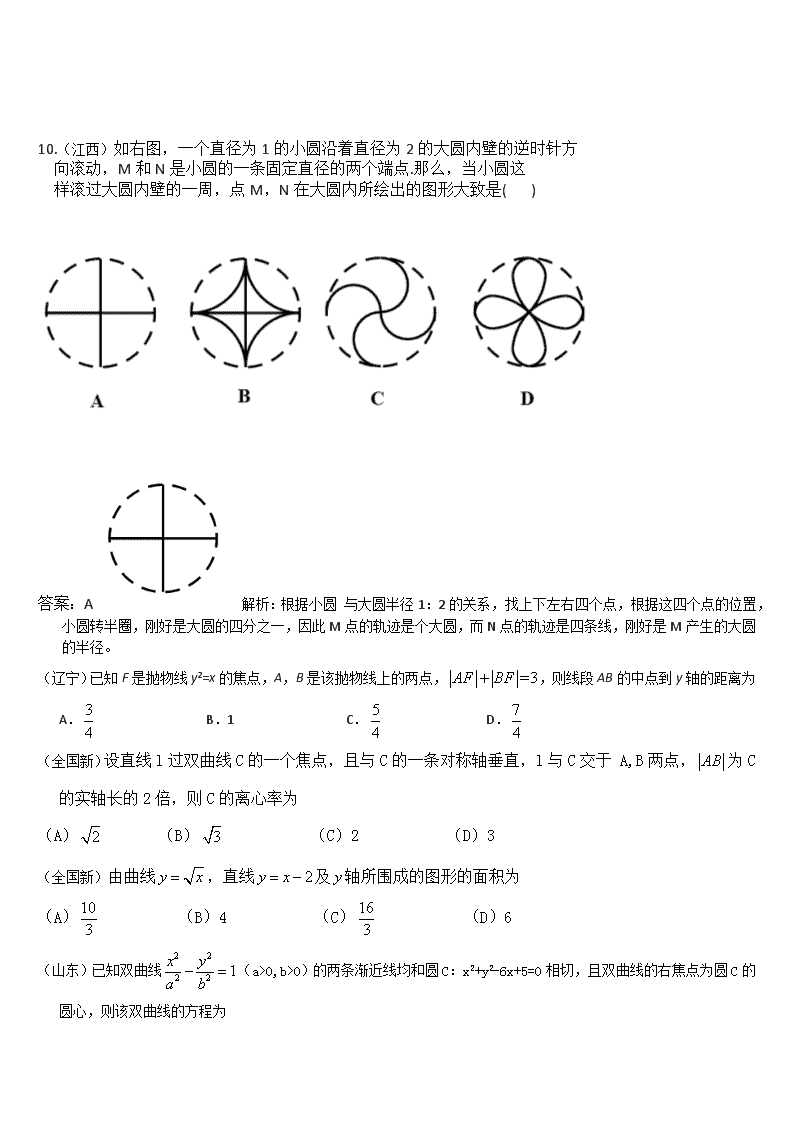
‎（安徽）双曲线的实轴长是（A）2 (B) (C) 4 (D) 4‎ ‎（福建）设圆锥曲线r的两个焦点分别为F1，F2，若曲线r上存在点P满足=4:3:2，则曲线r的离心率等于A. B.或‎2 C.2 D.‎ ‎（湖北）将两个顶点在抛物线上，另一个顶点是此抛物线焦点的正三角形个数记为n，则A. n=0 B. n=‎1 C. n=2 D. n 3‎ ‎（湖南）设双曲线的渐近线方程为，则的值为（ ）A．4 B．‎3 C．2 D．1答案：C 解析：由双曲线方程可知渐近线方程为，故可知。‎ ‎（江西）若曲线与曲线有四个不同的交点,则实数的取值范围是 ( ) ‎ ‎ A. B. C. D. ‎ 答案：B 曲线表示以为圆心，以1为半径的圆，曲线表示过定点，与圆有两个交点，故也应该与圆有两个交点，由图可以知道，临界情况即是与圆相切的时候，经计算可得，两种相切分别对应，由图可知，m的取值范围应是 10. ‎（江西）如右图，一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方 ‎ 向滚动，M和N是小圆的一条固定直径的两个端点.那么，当小圆这 ‎ 样滚过大圆内壁的一周，点M，N在大圆内所绘出的图形大致是( )‎ 答案：A 解析：根据小圆 与大圆半径1：2的关系，找上下左右四个点，根据这四个点的位置，小圆转半圈，刚好是大圆的四分之一，因此M点的轨迹是个大圆，而N点的轨迹是四条线，刚好是M产生的大圆的半径。‎ ‎（辽宁）已知F是抛物线y2=x的焦点，A，B是该抛物线上的两点，，则线段AB的中点到y轴的距离为 ‎ A． B．‎1 ‎ C． D．‎ ‎（全国新）设直线l过双曲线C的一个焦点，且与C的一条对称轴垂直，l与C交于 A,B两点，为C的实轴长的2倍，则C的离心率为 ‎（A） （B） （C）2 （D）3‎ ‎（全国新）由曲线，直线及轴所围成的图形的面积为 ‎（A） （B）4 （C） （D）6‎ ‎（山东）已知双曲线（a>0,b>0）的两条渐近线均和圆C：x2+y2-6x+5=0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为 ‎（A） （B） （C） （D）‎ ‎（天津）已知抛物线的参数方程为（为参数）若斜率为1的 直线经过抛物线的焦点，且与圆相切，‎ 则=________.‎ ‎（全国新）在平面直角坐标系中，椭圆的中心为原点，焦点在 轴上，离心率为。过的直线 交于两点，且的周长为16，那么的方程为 。‎ ‎（辽宁）已知点（2，3）在双曲线C：上，C的焦距为4，则它的离心率为 ．‎ ‎（全国2）曲线y=+1在点(0，2)处的切线与直线y=0和y=x围成的三角形的面积为 ‎(A) (B) (C) (D)1‎ ‎【思路点拨】利用导数求出点（0，2）切线方程然后分别求出与直线y=0与y=x的交点问题即可解决。‎ ‎【精讲精析】选A.切线方程是：,在直角坐标系中作出示意图，即得。‎ ‎（全国2）已知抛物线C：的焦点为F，直线与C交于A，B两点．则=‎ ‎(A) (B) (C) (D) ‎ ‎【思路点拨】方程联立求出A、B两点后转化为解三角形问题。‎ ‎【精讲精析】选D.‎ 联立，消y得，解得.‎ 不妨设A在x轴上方，于是A，B的坐标分别为(4,4),(1,-2),‎ 可求，利用余弦定理.‎ ‎（陕西）设抛物线的顶点在原点，准线方程为，则抛物线的方程是 （ ）‎ ‎ （A） （B） (C) (D) ‎ ‎（陕西）设（，），（，），…，（，）是变量和的个样本点，直线是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是【D】‎ ‎（A）和的相关系数为直线的斜率 ‎（B）和的相关系数在0到1之间 ‎（C）当为偶数时，分布在两侧的样本点的个数一定相同 ‎（D）直线过点 ‎（四川）在抛物线上取横坐标为，的两点，过这两点引一条割线，有平行于该割线的一条直线同时与抛物线和圆相切，则抛物线顶点的坐标为 ‎（A） （B） （C） （D）‎ ‎（浙江）已知椭圆与双曲线有公共的焦点，的一条渐近线与以的长轴为直径的圆相交于两点，若恰好将线段三等分，则 ‎ A． B． C． D．‎ ‎（重庆）‎ ‎（重庆）设圆C位于抛物线与直线x=3所围成的封闭区域（包含边界）内，则椭圆半径能取到的最大值为__________‎ ‎（浙江）设为实数，若则的最大值是 ．。‎ ‎（浙江）设分别为椭圆的左、右焦点，点在椭圆上，若;则点的坐标是 ．‎ ‎（四川）双曲线P到左准线的距离是 . ‎ ‎（全国2）已知F1、F2分别为双曲线C: - =1的左、右焦点，点A∈C，点M的坐标为(2，0)，AM为∠F1AF2的平分线．则|AF2| = .‎ ‎【思路点拨】本题用内角平分线定理及双曲线的定义即可求解。‎ ‎【精讲精析】6.‎ 由角平分线定理得：,故.‎ ‎（江西）若椭圆的焦点在x轴上，过点作圆的切线，切点分别为A，B，直线AB恰好经过椭圆的右焦点和上顶点，则椭圆方程是 .‎ 答案： 解析：设过点（1，）的直线方程为：当斜率存在时，，‎ 根据直线与圆相切，圆心（0,0）到直线的距离等于半径1可以得到k=,直线与圆方程的联立可以得到切点的坐标（），当斜率不存在时，直线方程为：x=1，根据两点A：（1,0），B：（）可以得到直线：2x+y-2=0,则与y轴的交点即为上顶点坐标（2,0），与x轴的交点即为焦点，根据公式，即椭圆方程为：‎ ‎（PS:此题可能算是填空题，比较纠结的一道，因为要理清思路，计算有些繁琐。但是，是不是就做不出来呢，不是的，在我们寒假题海班的时候讲过一道与此相似的题型，也就在理科教材第147页第23题。所以最纠结的一道高考题也不过如此，你们还怕什么？）‎ ‎（江苏）在平面直角坐标系中，过坐标原点的一条直线与函数的图象交于P、Q两点，则线段PQ长的最小值是________‎ ‎（江苏）在平面直角坐标系中，已知点P是函数的图象上的动点，该图象在P处的切线交y轴于点M，过点P作的垂线交y轴于点N，设线段MN的中点的纵坐标为t，则t的最大值是_____________‎ ‎（重庆）如题（20）图，椭圆的中心为原点，离心率，一条准线的方程为.‎ ‎ （Ⅰ）求该椭圆的标准方程；‎ ‎(Ⅱ) 设动点满足：，其中是椭圆上的点，直线与的斜率之积为，问：是否存在两个定点，使得为定值？若存在，求的坐标；若不存在，说明理由.‎ ‎ ‎ ‎（上海）设为常数，若点是双曲线的一个焦点，则 。‎ ‎（浙江）已知抛物线:＝，圆:的圆心为点M ‎（Ⅰ）求点M到抛物线的准线的距离；‎ ‎（Ⅱ）已知点P是抛物线上一点（异于原点），过点P作圆的两条切线，交抛物线于A，B两点，若过M，P两点的直线垂直于AB，求直线的方程 本题主要考查抛物线的几何性质，直线与抛物线、圆的位置关系等基础知识，同时考查解析几何的基本思想方法和综合解题能力。满分15分。‎ ‎ （I）解：由题意可知，抛物线的准线方程为： ‎ 所以圆心M（0，4）到准线的距离是 ‎（II）解：设，则题意得，‎ 设过点P的圆C2的切线方程为，‎ 即 ①‎ 则即，‎ 设PA，PB的斜率为，则是上述方程的两根，所以 将①代入由于是此方程的根，故，所以 由，得，解得即点P的坐标为 ‎，所以直线的方程为 ‎（天津）在平面直角坐标系中，点为动点，分别为椭圆的左右焦点．已知△为等腰三角形．‎ ‎（Ⅰ）求椭圆的离心率；‎ ‎（Ⅱ）设直线与椭圆相交于两点，是直线上的点，满足，求点的轨迹方程．‎ 本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面向量等基础知识，考查用代数方法研究圆锥曲线的性质及数形结合的数学思想，考查解决问题能力与运算能力.满分13分.‎ ‎ （I）解：设 由题意，可得即 整理得（舍），或所以 ‎（II）解：由（I）知可得椭圆方程为直线PF2方程为 A，B两点的坐标满足方程组消去y并整理，得解得 ‎ 得方程组的解不妨设 设点M的坐标为，‎ 由于是由即，化简得 将所以 因此，点M的轨迹方程是 ‎（四川）椭圆有两顶点A(-1，0)、B(1，0)，过其焦点F(0，1)的直线l与椭圆交于C、D两点，并与x轴交于点P．直线AC与直线BD交于点Q．‎ ‎ (I)当|CD | = 时，求直线l的方程；‎ ‎ (II)当点P异于A、B两点时，求证：OP·OQ 为定值。‎ ‎ ‎ ‎（陕西）如图，设P是圆上的动点，点D是P在x轴上的摄影，M为PD上一点，且 ‎（Ⅰ）当P在圆上运动时，求点M的轨迹C的方程 ‎（Ⅱ）求过点（3，0）且斜率为的直线被C所截线段的长度 解：（Ⅰ）设M的坐标为（x,y）P的坐标为（xp,yp）‎ 由已知 xp=x ‎ ‎ ‎∵  P在圆上， ∴   ，即C的方程为 ‎（Ⅱ）过点（3，0）且斜率为的直线方程为，‎ 设直线与C的交点为 将直线方程代入C的方程，得 ‎ 即 ‎ ∴    ‎ ‎  ∴   线段AB的长度为 ‎ 注：求AB长度时，利用韦达定理或弦长公式求得正确结果，同样得分。‎ ‎（陕西）如图，从点P1（0,0）作x轴的垂线交于曲线y=ex于点Q1（0,1），曲线在Q1点处的切线与x轴交与点P2。再从P2作x轴的垂线交曲线于点Q2，依次重复上述过程得到一系列点：P1，QI；P2，Q2…Pn，Qn，记点的坐标为（，0）（k=1,2，…，n）。‎ ‎（Ⅰ）试求与的关系（2≤k≤n）；‎ ‎（ Ⅱ）求 解（Ⅰ）设，由得点处切线方程为 由得。‎ ‎（ Ⅱ），得，‎ ‎（山东）已知直线l与椭圆C: 交于P.Q两不同点，且△OPQ的面积S=‎ ‎,其中Q为坐标原点。‎ ‎（Ⅰ）证明X12+X22和Y12+Y22均为定值 ‎（Ⅱ）设线段PQ的中点为M，求的最大值；‎ ‎（Ⅲ）椭圆C上是否存在点D,E,G，使得S△ODE=S△ODG=S△OEG若存在，判断△DEG的形状；若不存在，请说明理由。‎ ‎（全国新）在平面直角坐标系xOy中，已知点A(0,-1)，B点在直线y = -3上，M点满足MB//OA， MA•AB = MB•BA，M点的轨迹为曲线C。‎ ‎（Ⅰ）求C的方程；‎ ‎（Ⅱ）P为C上的动点，l为C在P点处得切线，求O点到l距离的最小值。‎ 解：‎ ‎ (Ⅰ)设M(x,y),由已知得B(x,-3),A(0,-1).所以=（-x,-1-y）, =(0,-3-y), =(x,-2).再由愿意得知（+）• =0,即（-x,-4-2y）• (x,-2)=0.‎ 所以曲线C的方程式为y=x-2.‎ ‎(Ⅱ)设P(x,y)为曲线C：y=x-2上一点，因为y=x,所以的斜率为x 因此直线的方程为，即。‎ 则O点到的距离.又，所以 当=0时取等号，所以O点到距离的最小值为2.‎ ‎（北京）曲线C是平面内与两个定点F1（-1，0）和F¬2（1，0）的距离的积等于常数的点的轨迹.给出下列三个结论：‎ ‎ ① 曲线C过坐标原点；‎ ‎ ② 曲线C关于坐标原点对称；‎ ‎ ③若点P在曲线C上，则△FPF的面积大于a。‎ 其中，所有正确结论的序号是 ‎ ‎（辽宁）已知O为坐标原点，F为椭圆在y轴正半轴上的焦点，过F且斜率为的直线与C交与A、B两点，点P满足 ‎(Ⅰ)证明：点P在C上；‎ ‎（Ⅱ）设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上.‎ ‎【思路点拨】方程联立利用韦达定理是解决这类问题的基本思路，注意把用坐标表示后求出P点的坐标，然后再结合直线方程把P点的纵坐标也用A、B两点的横坐标表示出来。从而求出点P的坐标代入椭圆方程验证即可证明点P在C上。(II)此问题证明有两种思路：思路一：关键是证明互补.通过证明这两个角的正切值互补即可，再求正切值时要注意利用倒角公式。‎ 思路二：根据圆的几何性质圆心一定在弦的垂直平分线上，所以根据两条弦的垂直平分线的交点找出圆心N，然后证明N到四个点A、B、P、Q的距离相等即可.‎ ‎【精讲精析】 (I)设 直线，与联立得 由得 ‎,‎ 所以点P在C上。‎ ‎（II）法一：‎ 同理 所以互补，‎ 因此A、P、B、Q四点在同一圆上。‎ 法二：由和题设知，,PQ的垂直平分线的方程为…①‎ 设AB的中点为M，则，AB的垂直平分线的方程为…②‎ 由①②得、的交点为 ‎,‎ ‎,,‎ 故.‎ 所以A、P、B、Q四点在同一圆圆N上.‎ ‎（辽宁）如图，已知椭圆C1的中心在原点O，长轴左、右端点M，N在x轴上，椭圆C2的短轴为MN，且C1，C2的离心率都为e，直线l⊥MN，l与C1交于两点，与C2交于两点，这四点按纵坐标从大到小依次为A，B，C，D．‎ ‎ （I）设，求与的比值；‎ ‎ （II）当e变化时，是否存在直线l，使得BO∥AN，并说明理由．‎ 解：（I）因为C1，C2的离心率相同，故依题意可设 设直线，分别与C1，C2的方程联立，求得 ‎ ………………4分 当表示A，B的纵坐标，可知 ‎ ………………6分 ‎ （II）t=0时的l不符合题意.时，BO//AN当且仅当BO的斜率kBO与AN的斜率kAN相等，即 解得 因为 所以当时，不存在直线l，使得BO//AN；‎ 当时，存在直线l使得BO//AN. ………………12分 ‎（江西）是双曲线：上一点，分别是双曲线的左、右定点，直线的斜率之积为.‎ （1） 求双曲线的离心率；‎ （2） 过双曲线的右焦点且斜率为1的直线交双曲线于两点，为坐标原点，为双曲线上的一点，满足，求的值.‎ 解：（1）已知双曲线E：，在双曲线上，M，N分别为双曲线E的左右顶点，所以，，直线PM，PN斜率之积为 而，比较得 ‎（2）设过右焦点且斜率为1的直线L：，交双曲线E于A，B两点，则不妨设，又，点C在双曲线E上：‎ ‎*（1）‎ 又 联立直线L和双曲线E方程消去y得：‎ 由韦达定理得：，代入（1）式得：‎ ‎（江苏）、如图，在平面直角坐标系中，M、N分别是椭圆的顶点，过坐标原点的直线交椭圆于P、A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连接AC，并延长交椭圆于点B，设直线PA的斜率为k N M P A x y B C ‎（1）当直线PA平分线段MN，求k的值；‎ ‎（2）当k=2时，求点P到直线AB的距离d；‎ ‎（3）对任意k>0，求证：PA⊥PB ‎（湖南）如图7，椭圆的离心率为，轴被曲线 截得的线段长等于的长半轴长。‎ ‎（Ⅰ）求，的方程；‎ ‎（Ⅱ）设与轴的交点为M，过坐标原点O的直线与相交于点A,B,直线MA,MB分别与相交与D,E.‎ ‎（i）证明：；‎ ‎(ii)记△MAB,△MDE的面积分别是.问：是否存在直线,使得=?‎ 请说明理由。‎ 解析：（I）由题意知，从而，又，解得。‎ 故，的方程分别为。‎ ‎（II）（i）由题意知，直线的斜率存在，设为，则直线的方程为.‎ 由得，‎ 设，则是上述方程的两个实根，于是。‎ 又点的坐标为，所以 故，即。‎ ‎（ii）设直线的斜率为，则直线的方程为，由解得或，则点的坐标为 又直线的斜率为 ，同理可得点B的坐标为.‎ 于是 由得，‎ 解得或，则点的坐标为；‎ 又直线的斜率为，同理可得点的坐标 于是 因此 由题意知，解得 或。‎ 又由点的坐标可知，，所以 故满足条件的直线存在，且有两条，其方程分别为和。‎ ‎（湖北）如图，直角坐标系所在平面为，直角坐标系（其中与轴重合）所在的平面为，。‎ ‎（Ⅰ）已知平面内有一点，则点在平面内的射影的坐标为 ；‎ ‎（Ⅱ）已知平面内的曲线的方程是，则曲线在平面内的射影的方程是 。‎ ‎（湖北）平面内与两定点，连续的斜率之积等于非零常数的点的轨迹，加上、两点所成的曲线可以是圆、椭圆成双曲线.‎ ‎（Ⅰ）求曲线的方程，并讨论的形状与值得关系；‎ ‎（Ⅱ）当时，对应的曲线为；对给定的，对应的曲线为，设、是的两个焦点。试问：在撒谎个，是否存在点，使得△的面积。若存在，求的值；若不存在，请说明理由。‎ ‎（广东）设圆C与两圆中的一个内切，另一个外切.‎ ‎（1）求C的圆心轨迹L的方程.‎ ‎（2）已知点且P为L上动点，求的最大值及此时点P的坐标.‎ ‎（福建）已知直线l：y=x+m，m∈R。‎ ‎（I）若以点M（2,0）为圆心的圆与直线l相切与点P，且点P在y轴上，求该圆的方程；‎ ‎（II）若直线l关于x轴对称的直线为，问直线与抛物线C：x2=4y是否相切？说明理由。‎ ‎（安徽）设，点的坐标为（1,1），点在抛物线上运动，点满足，经过点与轴垂直的直线交抛物线于点，点满足,求点的轨迹方程。‎ ‎（北京）已知椭圆.过点（m,0）作圆的切线I交椭圆G于A，B两点.‎ ‎ （I）求椭圆G的焦点坐标和离心率；‎ ‎ （II）将表示为m的函数，并求的最大值.‎ 解：（Ⅰ）由已知得 所以 所以椭圆G的焦点坐标为 离心率为 ‎（Ⅱ）由题意知，.‎ 当时，切线l的方程，点A、B的坐标分别为 此时 当m=－1时，同理可得 当时，设切线l的方程为 由 设A、B两点的坐标分别为，则 又由l与圆 所以 由于当时，‎ 所以.‎ 因为 且当时，|AB|=2，所以|AB|的最大值为2.‎