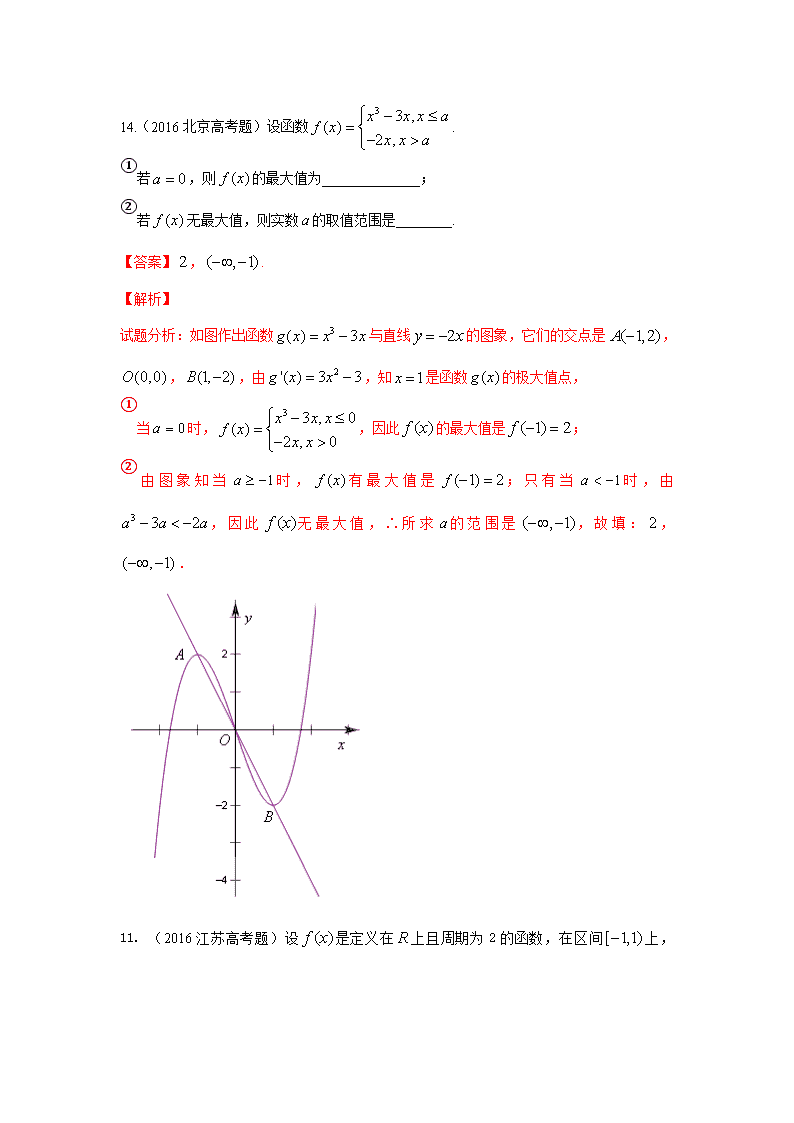高考题函数汇编 16页

‎14.（2016北京高考题）设函数.‎ ‎①若，则的最大值为______________；‎ ‎②若无最大值，则实数的取值范围是________.‎ ‎【答案】，.‎ ‎【解析】‎ 试题分析：如图作出函数与直线的图象，它们的交点是，，，由，知是函数的极大值点，‎ ‎①当时，，因此的最大值是；‎ ‎②由图象知当时，有最大值是；只有当时，由，因此无最大值，∴所求的范围是，故填：，．‎ ‎11. （2016江苏高考题）设是定义在上且周期为2的函数，在区间上，‎ ‎ ‎ 其中 若 ，则的值是 ▲ .‎ ‎【答案】‎ ‎【解析】，‎ 因此 ‎（8）（2016天津高考题）已知函数f（x）=（a>0,且a≠1）在R上单调递减，且关于x的方程恰好有两个不相等的实数解，则a的取值范围是（ ）‎ ‎（A）（0，] （B）[，] （C）[，]{}（D）[，）{}‎ ‎【答案】C ‎【解析】‎ 试题分析：由在上递减可知，由方程恰好有两个不相等的实数解，可知，，又∵时，抛物线与直线相切，也符合题意，∴实数的去范围是，故选C.‎ ‎（7）（2016全国卷1）函数在的图像大致为（ ）‎ ‎（A）（B）‎ ‎（C）（D）‎ ‎【答案】D 考点：函数图像与性质 ‎（8）（2016全国卷1）若,则（ ）‎ ‎（A） （B） （C） （D）‎ ‎【答案】C ‎【解析】‎ 试题分析：用特殊值法,令,,得,选项A错误,,选项B错误,,选项C正确,,选项D错误,故选C．‎ ‎（12）（2016全国卷2）已知函数满足，若函数与图像的交点为则（ ）‎ ‎（A）0 （B） （C） （D）‎ ‎【答案】B ‎(10) （2016全国卷2）下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（ ）‎ ‎（A）y=x （B）y=lgx （C）y=2x （D）‎ ‎【答案】D ‎【解析】‎ 试题分析：，定义域与值域均为，只有D满足，故选D．‎ ‎(12) （2016全国卷2）已知函数f(x)（x∈R）满足f(x)=f(2-x)，若函数y=|x2-2x-3| 与y=f(x) 图像的交点为（x1,y1），(x2,y2)，…，（xm,ym），则（ ）‎ ‎(A)0 (B)m (C) 2m (D) 4m ‎【答案】B ‎（7）（2016全国卷3）已知，则（ ）‎ ‎(A) (B) (C) (D) ‎ ‎【答案】A ‎【解析】‎ 试题分析：因为，，又函数在上是增函数，所以，即，故选A．[来源:学,科,网]‎ ‎（9）（2016山东高考题）已知函数f(x)的定义域为R.当x<0时， ；当 时，；当 时， .则f(6)= （ ）‎ ‎（A）−2 （B）−1 （C）0 （D）2‎ ‎【答案】D ‎【解析】‎ 试题分析：当时，,所以当时，函数是周期为 的周期函数，所以，又函数是奇函数，所以，故选D.‎ ‎（15）（2016山东高考题）已知函数 其中，若存在实数b，使得关于x的方程f（x）=b有三个不同的根，则m的取值范围是________________.‎ ‎【答案】 ‎ ‎【解析】‎ 试题分析：‎ 画出函数图象如下图所示：‎ 由图所示，要有三个不同的根，需要红色部分图像在深蓝色图像的下方，即，解得 ‎(9)（2016山东高考题） 已知函数f(x)的定义域为R.当x＜0时，f(x)=x3-1；当-1≤x≤1时，f(-x)= —f(x)；当x＞时，f(x+)=f(x—).则f(6)= （ ）‎ ‎（A）-2 （B）-1‎ ‎（C）0 （D）2‎ ‎【答案】D ‎【解析】‎ 试题分析：‎ 当时，，所以当时，函数是周期为的周期函数，所以，又因为当时，，所以，故选D.‎ ‎9. （2016四川高考题）设直线l1，l2分别是函数f(x)= 图象上点P1，P2处的切线，l1与l2垂直相交于点P，且l1，l2分别与y轴相交于点A，B，则△PAB的面积的取值范围是 ‎（A）(0,1) （B）(0,2) （C）(0,+∞) （D）(1,+∞)‎ ‎【答案】A ‎14. （2016四川高考题） 已知函数是定义在R上的周期为2的奇函数，当0＜x＜1时，，则= .‎ ‎【答案】-2‎ ‎12. （2016浙江高考题）已知a>b>1.若logab+logba=，ab=ba，则a= ，b= .‎ ‎【答案】 ‎ 考点：1、指数运算；2、对数运算．‎ ‎【易错点睛】在解方程时，要注意，若没注意到，方程 的根有两个，由于增根导致错误．‎ ‎5.（2016浙江高考题）已知a，b>0，且a≠1，b≠1，若 ，则（ ）‎ A. B. [来源:Z#xx#k.Com]‎ C. D. ‎ ‎【答案】D 考点：对数函数的性质.‎ ‎【易错点睛】在解不等式时，一定要注意对分为和 两种情况进行讨论，否则很容易出现错误．‎ ‎6. （2016浙江高考题）已知函数f（x）=x2+bx，则“b<‎0”‎是“f（f（x））的最小值与f（x）的最小值相等”的（ ）‎ A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎【答案】A ‎【解析】‎ 试题分析：由题意知，最小值为.‎ 令，则，‎ 当时，的最小值为，所以“”能推出“的最小值与的最小值相等”；‎ 当时，的最小值为0，的最小值也为0，所以“的最小值与的最小值相等”不能推出“”．故选A．‎ 考点：充分必要条件.‎ ‎7.（2016浙江高考题）已知函数满足：且.（ ）‎ A.若，则 B.若，则 C.若，则 D.若，则 ‎【答案】B ‎ 函数全国卷高考动向分析 ‎1.（2015全国文科2）‎ ‎（12）设函数 A. B. C. D. ‎ 解：因为函数 故选A.‎ ‎2.（2015全国卷文科2） ‎ ‎（13）已知函数 。‎ ‎13、答：a=-2‎ ‎3.（2014全国卷文科2）15．（5分）偶函数y=f（x）的图象关于直线x=2对称，f（3）=3，则f（﹣1）=　_________　．3‎ 函数奇偶性的性质．菁优网版权所有 函数的性质及应用．‎ 根据函数奇偶性和对称性的性质，得到f（x+4）=f（x），即可得到结论．‎ 解：因为偶函数y=f（x）的图象关于直线x=2对称，‎ 所以f（2+x）=f（2﹣x）=f（x﹣2），‎ 即f（x+4）=f（x），‎ 则f（﹣1）=f（﹣1+4）=f（3）=3，‎ 故答案为：3‎ ‎4．(2013课标全国Ⅱ，文12)若存在正数x使2x(x－a)＜1成立，则a的取值范围是(　　)．‎ A．(－∞，＋∞) B．(－2，＋∞) C．(0，＋∞) D．(－1，＋∞)‎ ‎5.（2012文科2）(11)当00}＝(　　)‎ A．{x|x<－2或x>4} B．{x|x<0或x>4} C．{x|x<0或x>6} D．{x|x<－2或x>2}‎ ‎8.解析：当x<0时，－x>0，∴f(－x)＝(－x)3－8＝－x3－8，‎ 又f(x)是偶函数，∴f(x)＝f(－x)＝－x3－8，‎ ‎∴f(x)＝.∴f(x－2)＝，‎ 或，解得x>4或x<0.‎ 答案：B ‎22.（2010理科2）11．已知函数f(x)＝若a，b，c互不相等，且f(a)＝f(b)＝f(c)，则abc的取值范围是(　　)‎ A．(1,10) B．(5,6) C．(10,12) D．(20,24)‎ ‎11.解析：由a，b，c互不相等，结合图象可知 ：‎ 这三个数分别在区间(0,1)，(1,10)，(10,12)上，‎ 不妨设a∈(0,1)，b∈(1,10)，c∈(10,12)，‎ 由f(a)＝f(b)得lga＋lgb＝0，‎ 即lgab＝0，所以ab＝1，所以abc∈(10,12)．‎ 答案：C ‎23.（2009理科2）用min{a,b,c}表示a,b,c三个数中的最小值设f（x）=min{, x+2,10-x} (x 0),则f（x）的最大值为 ‎（A）4 （B）5 （C）6 （D）7‎ 解析：选C ‎ 全国卷1‎ ‎1.（2015文科1）10、已知函数 ，且，则A ‎（A） （B） （C） （D）‎ ‎2.（2015文科1）12、设函数的图像与的图像关于直线对称，且，则( )C （A） ‎ （B） （C） （D）‎ ‎3.（2014文科1）设函数的定义域为，且是奇函数，是偶函数，则下列结论中正确的是 A. 是偶函数 B. 是奇函数 ‎ ‎ C. 是奇函数 D. 是奇函数 ‎【参考答案】：设，则，∵是奇函数，是偶函数，∴，为奇函数，选C.‎ ‎4.（2014文科1）（15）设函数则使得成立的的取值范围是________.‎ ‎【参考答案】当x <1时，由可得x -1£ ln 2，即x £ ln 2+1，故x <1；‎ 当x ³1时，由f (x) =£ 2可得x £ 8，故1£ x £ 8，综上可得x £ 8‎ ‎【解题方法】：①转化为解两个不等式组，最后取并集②画出函数的图像，只要找在直线y=2下方的图像对应的x的求值范围即为不等式的解集。‎ ‎【规律提炼】：解分段函数的不等式，可以分段解，也可以画出函数图像，用图像解 ‎5．(2013课标全国Ⅰ，文12)已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是(　　)．‎ A．(－∞，0] B．(－∞，1]‎ C．[－2,1] D．[－2,0]‎ 答案：D 解析：可画出|f(x)|的图象如图所示．‎ 当a＞0时，y＝ax与y＝|f(x)|恒有公共点，所以排除B，C；‎ 当a≤0时，若x＞0，则|f(x)|≥ax恒成立．‎ 若x≤0，则以y＝ax与y＝|－x2＋2x|相切为界限，‎ 由得x2－(a＋2)x＝0.‎ ‎∵Δ＝(a＋2)2＝0，∴a＝－2.‎ ‎∴a∈[－2,0]．故选D.‎ ‎6.（2015理科1）13．若函数f（x）=为偶函数，则a= ‎ ‎【答案】1‎ ‎【解析】由题知是奇函数，所以 =，解得=1.‎ 考点：函数的奇偶性 ‎7.（2014理科1）3.设函数，的定义域都为R，且是奇函数，是偶函数，则下列结论正确的是 ‎.是偶函数 .||是奇函数 ‎.||是奇函数 .||是奇函数 ‎【答案】：C ‎【解析】：设，则，∵是奇函数，是偶函数，∴，为奇函数，选C.‎ ‎8．(2013课标全国Ⅰ，理11)已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是(　　)．‎ A．(－∞，0] B．(－∞，1]‎ C．[－2,1] D．[－2,0]‎ 答案：D 解析：由y＝|f(x)|的图象知：‎ ‎①当x＞0时，y＝ax只有a≤0时，才能满足|f(x)|≥ax，可排除B，C.‎ ‎②当x≤0时，y＝|f(x)|＝|－x2＋2x|＝x2－2x.‎ 故由|f(x)|≥ax得x2－2x≥ax.‎ 当x＝0时，不等式为0≥0成立．‎ 当x＜0时，不等式等价于x－2≤a.‎ ‎∵x－2＜－2，∴a≥－2.‎ 综上可知：a∈[－2,0]．‎ ‎9．(2013课标全国Ⅰ，理16)若函数f(x)＝(1－x2)(x2＋ax＋b)的图像关于直线x＝－2对称，则f(x)的最大值为__________．‎ 答案：16‎ 解析：∵函数f(x)的图像关于直线x＝－2对称，‎ ‎∴f(x)满足f(0)＝f(－4)，f(－1)＝f(－3)，即 解得∴f(x)＝－x4－8x3－14x2＋8x＋15.由f′(x)＝－4x3－24x2－28x＋8＝0，‎ 得x1＝－2－，x2＝－2，x3＝－2＋.易知，f(x)在(－∞，－2－)上为增函数，在(－2－，－2)上为减函数，在(－2，－2＋)上为增函数，在(－2＋，＋∞)上为减函数．∴f(－2－)＝[1－(－2－)2][(－2－)2＋8(－2－)＋15]‎ ‎＝(－8－)(8－)＝80－64＝16.‎ f(－2)＝[1－(－2)2][(－2)2＋8×(－2)＋15]＝－3(4－16＋15)＝－9.‎ f(－2＋)＝[1－(－2＋)2][(－2＋)2＋8(－2＋)＋15]‎ ‎＝(－8＋)(8＋)‎ ‎＝80－64＝16.‎ 故f(x)的最大值为16.‎