拉格朗日中值定理在高考题中的妙用 6页

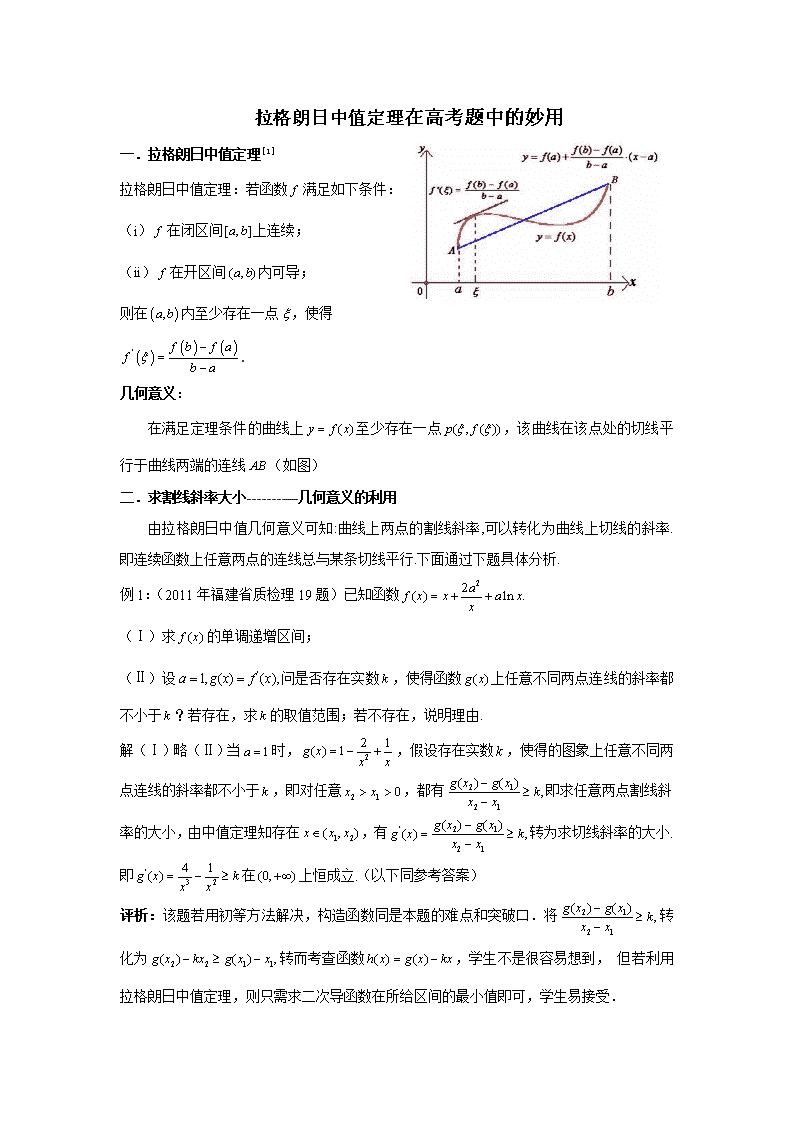
拉格朗日中值定理在高考题中的妙用 一．拉格朗日中值定理[1]‎ 拉格朗日中值定理：若函数满足如下条件：‎ ‎（i）在闭区间上连续；‎ ‎（ii）在开区间内可导；‎ 则在内至少存在一点，使得 .‎ 几何意义：‎ ‎ 在满足定理条件的曲线上至少存在一点，该曲线在该点处的切线平行于曲线两端的连线（如图）‎ 二．求割线斜率大小-----------几何意义的利用 由拉格朗日中值几何意义可知:曲线上两点的割线斜率,可以转化为曲线上切线的斜率.即连续函数上任意两点的连线总与某条切线平行.下面通过下题具体分析.‎ 例1：（2011年福建省质检理19题）已知函数 ‎（Ⅰ）求的单调递增区间；‎ ‎（Ⅱ）设问是否存在实数，使得函数上任意不同两点连线的斜率都不小于？若存在，求的取值范围；若不存在，说明理由.‎ 解（Ⅰ）略（Ⅱ）当时，，假设存在实数，使得的图象上任意不同两点连线的斜率都不小于，即对任意，都有即求任意两点割线斜率的大小，由中值定理知存在，有转为求切线斜率的大小.即在上恒成立.（以下同参考答案）‎ 评析：该题若用初等方法解决，构造函数同是本题的难点和突破口．将转化为转而考查函数，学生不是很容易想到， 但若利用拉格朗日中值定理，则只需求二次导函数在所给区间的最小值即可，学生易接受．‎ 二． 利用拉格朗日中值定理证最值 ‎（1）证或 ‎-------------即证与的大小关系 例2：（2009年辽宁卷理21题）‎ 已知函数 ‎（Ⅰ）讨论函数的单调性；‎ ‎（Ⅱ）证明：若，则对任意，，有.‎ ‎（Ⅰ）略；（Ⅱ）要证成立，即证. ‎ 令，则.由于，所以.从而在恒成立.也即.又，，故.则，即，也即.‎ ‎ 评注：这道题（Ⅱ）小题用初等方法做考虑函数.为什么考虑函数很多考生一下子不易想到.而且的放缩也不易想到.‎ ‎（2）、证明或成立（其中，）‎ ‎ ----------即证或 例3：（2007年高考全国卷I第20题）‎ 设函数.[2]‎ ‎（Ⅰ）证明：的导数；‎ ‎（Ⅱ）证明：若对所有，都有 ，则的取值范围是.‎ ‎（Ⅰ）略.（Ⅱ）证明：（i）当时，对任意的，都有 ‎(ii)当时，问题即转化为对所有恒成立.令，由拉格朗日中值定理知内至少存在一点（从而），使得，即，由于，故在上是增函数，让 得，所以的取值范围是.‎ 评注：用的是初等数学的方法.即令，再分和 两种情况讨论.其中，又要去解方程.但这有两个缺点：首先，为什么的取值范围要以为分界展开.其次，方程求解较为麻烦.但用拉格朗日中值定理求解就可以避开讨论，省去麻烦.‎ 例4：（2008年全国卷Ⅱ22题）设函数.‎ ‎（Ⅰ）求的单调区间；（Ⅱ）如果对任何，都有，求的取值范围.‎ 证明（Ⅰ）略； ‎ ‎（Ⅱ）证明：当时，显然对任何，都有；当时，‎ 由拉格朗日中值定理，知存在，使得.由（Ⅰ）知，从而.令得，；令得，.所以在上，的最大值在 上，的最大值.从而函数在上的最大值是.知，当时，的最大值为.所以，的最大值.为了使恒成立，应有.所以的取值范围是.‎ 评注：这道题的参考答案的解法是令,再去证明函数的最小值.这与上述的思路是一样的.但首先参考答案的解法中有个参数,要对参数进行分类讨论;其次为了判断的单调性,还要求和的解,‎ 这个求解涉及到反余弦,较为复杂.而用拉格朗日中值定理就可以避开麻烦，省去讨论.再次体现了高观点解题的优越性.‎ 三．利用拉格朗日中值定理证不等式 近几年的数学高考中，出现了不少含有拉格朗日中值定理的试题．常以不等式恒成立问题为基本切入点，具有一定的深度，既符合高考命题“能力立意”的宗旨，又突出了数学的学科特点，较好地甄别了学生的数学能力． 下面以近几年全国各地的数学高考试题为例，说明拉格朗日中值定理的不同形式在高考中不等式的应用，更好地体会用“高观点”解题的优势．‎ ‎（1）用于证明与的大小关系 例5：(2006年四川卷理第22题) [3]‎ 已知函数的导函数是，对任意两个不相等的正，证明：（Ⅱ）当时，.‎ 证明： 由得，，令则由拉格朗日中值定理得：‎ 下面只要证明：当时，任意,都有，则有，即证时，恒成立.这等价于证明的最小值大于.由，当且仅当时取到最小值，又，故时，恒成立.所以由拉格朗日定理得：.‎ 评注：这道题用初等数学的方法证明较为冗长，而且技巧性较强.因而思路较为突兀，大多数考生往往难以想到.相比之下，用拉格朗日中值定理证明，思路较为自然、流畅.体现了高观点解题的优越性，说明了学习高等数学的重要性.‎ ‎（2）证明，，三者大小的关系 例6：（2004年四川卷第22题）[3]‎ 已知函数.（Ⅰ）求函数的最大值；‎ ‎（Ⅱ）设，证明：.‎ 证明（Ⅰ）略； （Ⅱ）证明：依题意，有，‎ ‎ 由拉格朗日中值定理得，‎ 存在，使得 ‎ 评注：对于不等式中含有的形式，我们往往可以把和，分别对和两次运用拉格朗日中值定理.‎ 例7：(2006年四川卷理第22题)‎ 已知函数的导函数是，对任意两个不相等的正数，证明：（Ⅰ）当时，‎ 证明：（Ⅰ）不妨设，即证．由拉格朗日中值定理知，存在，则且，又， .当时，.所以是一个单调递减函数，故从而成立，因此命题获证．‎ 四：利用拉格朗日定理证明根的存在[4]‎ 证明方程根的存在性,所给根的范围就是区间把所给方程设为函数就可用拉格朗日中值定理证明方程根的存在性,一般用反证法.‎ 例1　设在可导,且,又对于内所有的点有证明方程在内有唯一的实根.‎ 分析:要证明方程有唯一的实根,分两步证明,先证明有根,再证明根是唯一的 证明:先证方程有根,‎ 令,又因为,则,得到g(0)·g(1)< 0.‎ 所以,函数g(x)在(0,1)内至少有一个实根.‎ 再证唯一性；假设方程在(0,1)内有两个实根不妨设为,‎ 则有,对函数)在上运用拉格朗日中值定理有 ‎.因此 这和已知条件矛盾.所以方程在(0,1)内有唯一的实根.‎