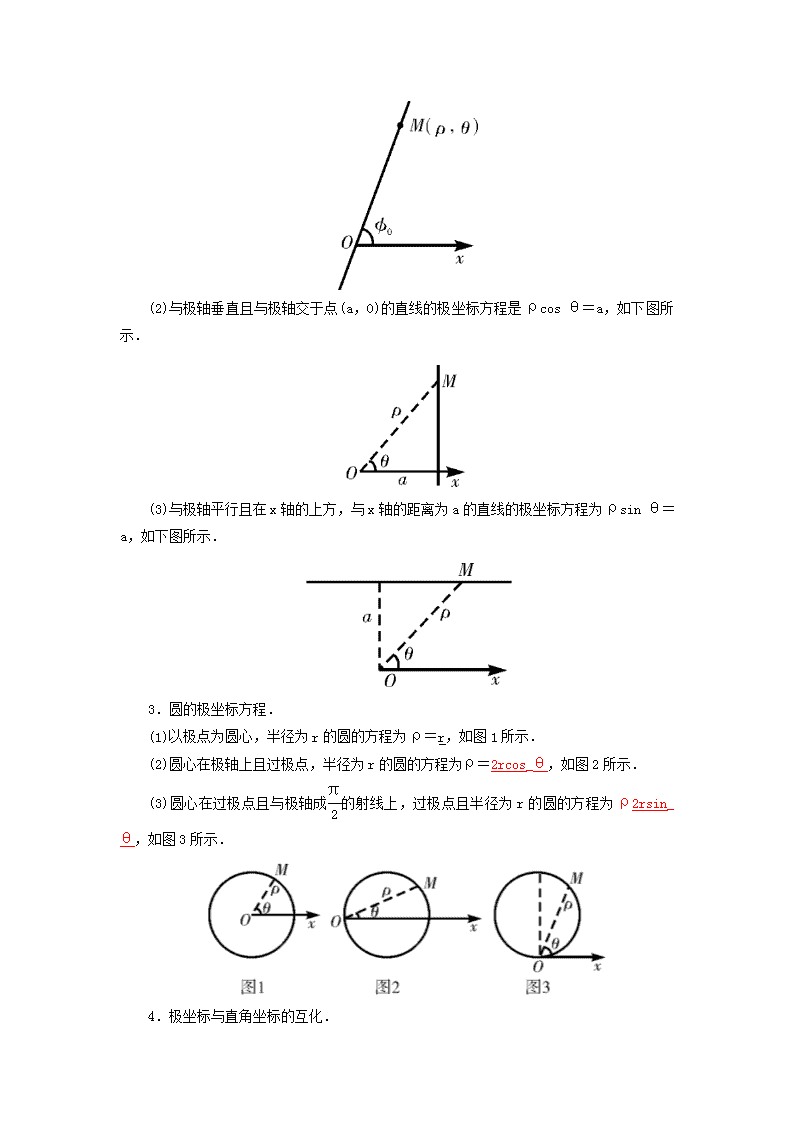高考文科数学复习专题 极坐标与参数方程 7页

‎1．曲线的极坐标方程．‎ ‎(1)极坐标系：一般地，在平面上取一个定点O，自点O引一条射线Ox，同时确定一个长度单位和计算角度的正方向(通常取逆时针方向为正方向)，这样就建立了一个极坐标系．其中，点O称为极点，射线Ox称为极轴．‎ ‎(2)极坐标(ρ，θ)的含义：设M是平面上任一点，ρ表示OM的长度，θ表示以射线Ox为始边，射线OM为终边所成的角．那么，有序数对(ρ，θ)称为点M的极坐标．显然，每一个有序实数对(ρ，θ)，决定一个点的位置．其中ρ称为点M的极径，θ称为点M的极角．‎ 极坐标系和直角坐标系的最大区别在于：在直角坐标系中，平面上的点与有序数对之间的对应关系是一一对应的，而在极坐标系中，对于给定的有序数对(ρ，θ)，可以确定平面上的一点，但是平面内的一点的极坐标却不是唯一的．‎ ‎(3)曲线的极坐标方程：一般地，在极坐标系中，如果平面曲线C上的任意一点的极坐标满足方程f(ρ，θ)＝0，并且坐标适合方程f(ρ，θ)＝0的点都在曲线C上，那么方程f(ρ，θ)＝0叫做曲线C的极坐标方程．‎ ‎2．直线的极坐标方程．‎ ‎(1)过极点且与极轴成φ0角的直线方程是θ＝φ0和θ＝π－φ0，如下图所示．‎ ‎(2)与极轴垂直且与极轴交于点(a，0)的直线的极坐标方程是ρcos θ＝a，如下图所示．‎ ‎(3)与极轴平行且在x轴的上方，与x轴的距离为a的直线的极坐标方程为ρsin θ＝a，如下图所示．‎ ‎3．圆的极坐标方程．‎ ‎(1)以极点为圆心，半径为r的圆的方程为ρ＝r，如图1所示．‎ ‎(2)圆心在极轴上且过极点，半径为r的圆的方程为ρ＝2rcos_θ，如图2所示．‎ ‎(3)圆心在过极点且与极轴成的射线上，过极点且半径为r的圆的方程为ρ2rsin_θ，如图3所示．‎ ‎4．极坐标与直角坐标的互化．‎ 若极点在原点且极轴为x轴的正半轴，则平面内任意一点M的极坐标M(ρ，θ)化为平面直角坐标M(x，y)的公式如下：‎ 或者ρ＝，tan θ＝，‎ 其中要结合点所在的象限确定角θ的值．‎ ‎1．曲线的参数方程的定义．‎ 在平面直角坐标系中，如果曲线上任意一点的坐标x，y都是某个变数t的函数，即并且对于t的每一个允许值，由方程组所确定的点M(x，y)都在这条曲线上，那么方程组就叫做这条曲线的参数方程，联系x，y之间关系的变数t叫做参变数，简称参数．‎ ‎2．常见曲线的参数方程．‎ ‎(1)过定点P(x0，y0)，倾斜角为α的直线：‎ (t为参数)，‎ 其中参数t是以定点P(x0，y0)为起点，点M(x，y)为终点的有向线段PM的数量，又称为点P与点M间的有向距离．‎ 根据t的几何意义，有以下结论：‎ ‎①设A，B是直线上任意两点，它们对应的参数分别为tA和tB，则|AB|＝|tB－tA|＝；‎ ‎②线段AB的中点所对应的参数值等于.‎ ‎(2)中心在P(x0，y0)，半径等于r的圆：‎ (θ为参数)‎ ‎(3)中心在原点，焦点在x轴(或y轴)上的椭圆：‎ (θ为参数).‎ 中心在点P(x0，y0)，焦点在平行于x轴的直线上的椭圆的参数方程为(α为参数)．‎ ‎(4)中心在原点，焦点在x轴(或y轴)上的双曲线：‎ (θ为参数).‎ ‎(5)顶点在原点，焦点在x轴的正半轴上的抛物线：‎ (t为参数，p>0)．‎ 注：sec θ＝.‎ ‎3．参数方程化为普通方程．‎ 由参数方程化为普通方程就是要消去参数，消参数时常常采用代入消元法、加减消元法、乘除消元法、三角代换法，消参数时要注意参数的取值范围对x，y的限制．‎ ‎　　　　　　　　　　　　　　　　‎ ‎1．已知点A的极坐标为，则点A的直角坐标是(2，－2)．‎ ‎2．把点P的直角坐标(，－)化为极坐标，结果为．‎ ‎3．曲线的极坐标方程ρ＝4sin θ化为直角坐标方程为x2＋(y－2)2＝4．‎ ‎4．以极坐标系中的点为圆心、1为半径的圆的极坐标方程是ρ＝2cos．‎ ‎5．在平面直角坐标系xOy中，若直线l：(t为参数)过椭圆C：(θ为参数)的右顶点，则常数a的值为3．‎ 解析：由直线l：得y＝x－a.由椭圆C：得＝＝1.所以椭圆C的右顶点为(3，0)．因为直线l过椭圆的右顶点，所以0＝3－a，即a＝3.‎ 一、选择题 ‎1．在平面直角坐标系xOy中，点P的直角坐标为(1，－)．若以原点O为极点，x 轴正半轴为极轴建立极坐标系，则点P的极坐标可以是(C)‎ A. B. C. D. ‎2．若圆的方程为(θ为参数)，直线的方程为(t为参数)，则直线与圆的位置关系是(B)‎ A．相离 B．相交 C．相切 D．不能确定 ‎3．以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知直线l的参数方程是(t为参数)，圆C的极坐标方程是ρ＝4cos θ，则直线l被圆C截得的弦长为(D)‎ A. B．2 C. D．2 解析：由题意可得直线和圆的方程分别为x－y－4＝0，x2＋y2＝4x，所以圆心C(2，0)，半径r＝2，圆心(2，0)到直线l的距离d＝，由半径，圆心距，半弦长构成直角三角形，解得弦长为2.‎ ‎4．已知动直线l平分圆C：(x－2)2＋(y－1)2＝1，则直线l与圆O：(θ为参数)的位置关系是(A)‎ A．相交 B．相切 C．相离 D．过圆心 解析：动直线l平分圆C：(x－2)2＋(y－1)2＝1，即圆心(2，1)在直线l上，又圆O：的普通方程为x2＋y2＝9且22＋12<9，故点(2，1)在圆O内，则直线l与圆O的位置关系是相交．‎ 二、填空题 ‎5．在平面直角坐标系xOy中，已知曲线C的参数方程是(θ是参数)，若以O为极点，x轴的正半轴为极轴，则曲线C的极坐标方程可写为ρ2＋4ρsin_θ＋3＝0．‎ 解析：在平面直角坐标系xOy中，(θ是参数)，∴根据sin2θ＋cos2θ＝1，可得x2＋(y＋2)2＝1，即x2＋y2＋4y＋3＝0.∴曲线C的极坐标方程为ρ2＋4ρsin θ＋3＝0.‎ ‎6．在平面直角坐标系中圆C的参数方程为(θ为参数)，以原点O为极点，以x轴的正半轴为极轴建立极坐标系，则圆C的圆心的极坐标为．‎ 三、解答题 ‎7．求极点到直线ρ＝(ρ∈R)的距离．‎ 解析：由ρ＝⇒ρsin θ＋ρcos θ＝1⇒x＋y＝1，‎ 故d＝＝.‎ ‎8．极坐标系中，A为曲线ρ2＋2ρcos θ－3＝0上的动点，B为直线ρcos θ＋ρsin θ－7＝0上的动点，求|AB|的最小值．‎ ‎9．(2015·大连模拟)曲线C1的参数方程为(θ为参数)，将曲线C1上所有点的横坐标伸长为原来的2倍，纵坐标伸长为原来的倍，得到曲线C2.以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ(cos θ－2sin θ)＝6.‎ ‎(1)求曲线C2和直线l的普通方程；‎ ‎(2)P为曲线C2上任意一点，求点P到直线l的距离的最值．‎ 解析：(1)由题意可得C2的参数方程为(θ为参数)，即C2：＋＝1，‎ 直线l：ρ(cos θ－2sin θ)＝6化为直角坐标方程为x－2y－6＝0.‎ ‎(2)设点P(2cos θ，sin θ)，由点到直线的距离公式得点P到直线l的距离为 d＝ ‎＝ ‎＝ ‎＝.‎ 所以≤d≤2，故点P到直线l的距离的最大值为2，最小值为.‎ ‎10．已知在直角坐标系xOy中，曲线C的参数方程为(θ为参数)，直线l经过定点P(3，5)，倾斜角为.‎ ‎(1)写出直线l的参数方程和曲线C的标准方程．‎ ‎(2)设直线l与曲线C相交于A，B两点，求|PA|·|PB|的值．‎ 解析：(1)由曲线C的参数方程(θ为参数)，得普通方程为(x－1)2＋(y－2)2＝16，即x2＋y2－2x－4y＝11＝0.‎ 直线l经过定点P(3，5)，倾斜角为，直线的参数方程为(t是参数)．‎ ‎(2)将直线的参数方程代入x2＋y2－2x－4y－11＝0，整理，得t2＋(2＋3)t－3＝0，设方程的两根分别为t1，t2，则t1t2＝－3，‎ 因为直线l与曲线C相交于A，B两点，所以|PA|·|PB|＝|t1t2|＝3.‎