吉林省实验中学高考数学模拟试卷理科九解析 22页

2016 年吉林省实验中学高考数学模拟试卷（理科）（九） 　 一、选择题：（本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中， 只有一项是符合题目要求的） 1．设集合 A={x|1＜x＜4}，集合 B={x|x2﹣2x﹣3≤0}，则 A∩（∁RB）=（　　） A．（1，4）B．（3，4）C．（1，3）D．（1，2）∪（3，4） 2．已知命题 p：∀x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）≥0，则￢p 是（　　） A．∃x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）≤0B．∀x1，x2∈R，（f（x2）﹣f（x1）） （x2﹣x1）≤0 C．∃x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）＜0D．∀x1，x2∈R，（f（x2）﹣f（x1）） （x2﹣x1）＜0 3．若复数 z 满足 z（2﹣i）=11+7i（i 为虚数单位），则 z 为（　　） A．3+5iB．3﹣5iC．﹣3+5iD．﹣3﹣5i 4．已知{an}是等差数列，公差 d 不为零，前 n 项和是 Sn，若 a3，a4，a8 成等比数列，则（　　） A．a1d＞0，dS4＞0B．a1d＜0，dS4＜0C．a1d＞0，dS4＜0D．a1d＜0，dS4＞0 5．已知 x，y 满足约束条件 ，若 z=ax+y 的最大值为 4，则 a=（　　） A．3B．2C．﹣2D．﹣3 6．阅读如图所示的程序图，运行相应的程序输出的结果 s=（　　） A．1B．4C．9D．16 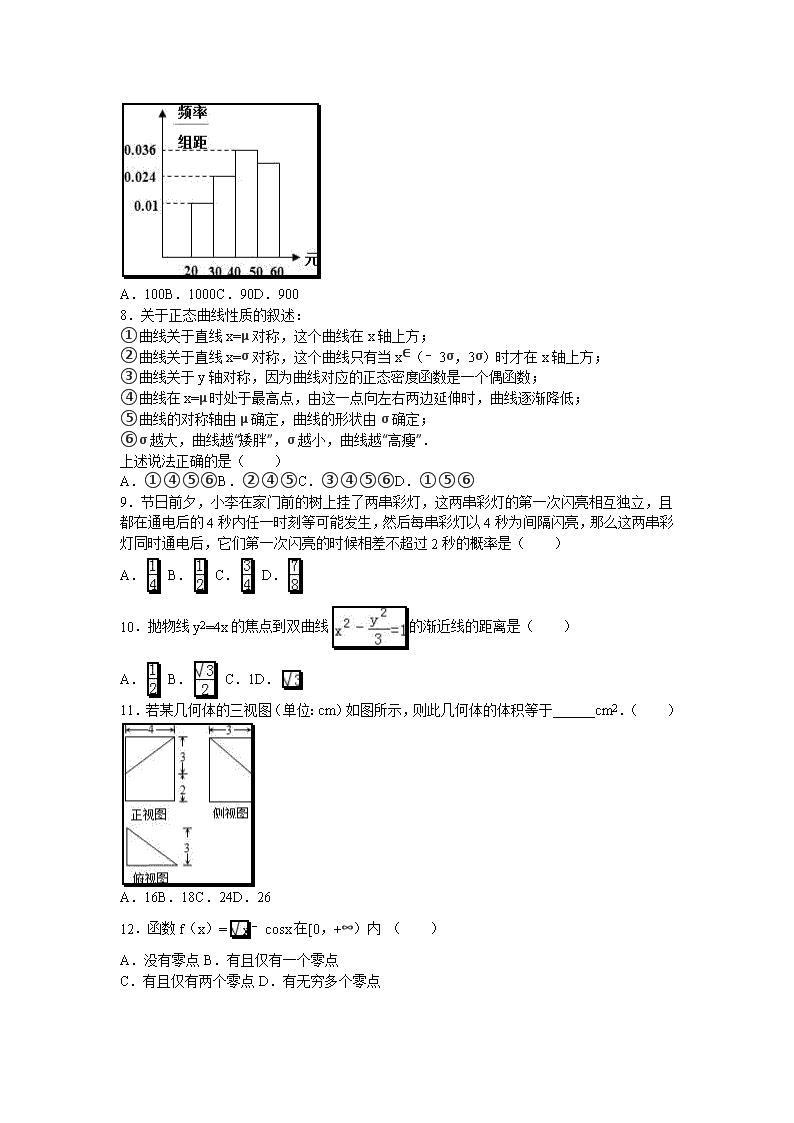7．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为 n 的样本，其频率分 布直方图如图所示，其中支出在[50，60）元的同学有 30 人，则 n 的值为（　　） A．100B．1000C．90D．900 8．关于正态曲线性质的叙述： ①曲线关于直线 x=μ 对称，这个曲线在 x 轴上方； ②曲线关于直线 x=σ 对称，这个曲线只有当 x∈（﹣3σ，3σ）时才在 x 轴上方； ③曲线关于 y 轴对称，因为曲线对应的正态密度函数是一个偶函数； ④曲线在 x=μ 时处于最高点，由这一点向左右两边延伸时，曲线逐渐降低； ⑤曲线的对称轴由 μ 确定，曲线的形状由 σ 确定； ⑥σ 越大，曲线越“矮胖”，σ 越小，曲线越“高瘦”． 上述说法正确的是（　　） A．①④⑤⑥B．②④⑤C．③④⑤⑥D．①⑤⑥ 9．节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且 都在通电后的 4 秒内任一时刻等可能发生，然后每串彩灯以 4 秒为间隔闪亮，那么这两串彩 灯同时通电后，它们第一次闪亮的时候相差不超过 2 秒的概率是（　　） A． B． C． D． 10．抛物线 y2=4x 的焦点到双曲线 的渐近线的距离是（　　） A． B． C．1D． 11．若某几何体的三视图（单位：cm）如图所示，则此几何体的体积等于______cm2．（　　） A．16B．18C．24D．26 12．函数 f（x）= ﹣cosx 在[0，+∞）内 （　　） A．没有零点 B．有且仅有一个零点 C．有且仅有两个零点 D．有无穷多个零点 　 二、填空题：（本大题共 4 小题，每小题 5 分，共 20 分） 13．已知向量 夹角为 45°，且 ，则 =　　　　　　． 14．（1+x）8（1+y）4 的展开式中 x2y2 的系数是　　　　　　． 15． sinxdx=　　　　　　． 16．已知半球内有一内接正方体，则这个半球的表面积与正方体的表面积之比 是　　　　　　． 　 三、解答题：（本大题共 5 小题，共 70 分．解答应写出说明文字，证明过程或演算步骤） 17．在平面直角坐标系 xOy 中，已知向量 =（ ，﹣ ）， =（sinx，cosx），x∈（0， ）． （1）若 ⊥ ，求 tanx 的值； （2）若 与 的夹角为 ，求 x 的值． 18．在一场娱乐晚会上，有 5 位民间歌手（1 至 5 号）登台演唱，由现场数百名观众投票选 出最受欢迎歌手．各位观众须彼此独立地在选票上选 3 名歌手，其中观众甲是 1 号歌手的歌 迷，他必选 1 号，不选 2 号，另在 3 至 5 号中随机选 2 名．观众乙和丙对 5 位歌手的演唱没 有偏爱，因此在 1 至 5 号中随机选 3 名歌手． （Ⅰ） 求观众甲选中 3 号歌手且观众乙未选中 3 号歌手的概率； （Ⅱ） X 表示 3 号歌手得到观众甲、乙、丙的票数之和，求 X 的分布列和数学期望． 19．如图，在直三棱柱 A1B1C1﹣ABC 中，AB⊥AC，AB=AC=2，AA1=4，点 D 是 BC 的中 点． （1）求异面直线 A1B 与 C1D 所成角的余弦值； （2）求平面 ADC1 与 ABA1 所成二面角的正弦值． 20．如图，点 P（0，﹣1）是椭圆 C1： + =1（a＞b＞0）的一个顶点，C1 的长轴是 圆 C2：x2+y2=4 的直径，l1，l2 是过点 P 且互相垂直的两条直线，其中 l1 交圆 C2 于 A、B 两 点，l2 交椭圆 C1 于另一点 D． （1）求椭圆 C1 的方程； （2）求△ABD 面积的最大值时直线 l1 的方程． 21．设 x1，x2（x1≠x2）是函数 f（x）=ax3+bx2﹣a2x（a＞0）的两个极值点． （1）若 x1=﹣1，x2=2，求函数 f（x）的解析式； （2）若 ，求 b 的最大值． （3）若 x1＜x＜x2，且 x2=a，g（x）=f'（x）﹣a（x﹣x1），求证： ． 　 请考生在第 22，23，24 三题中任选一题作答，如果多做，则按所做的第一题计分．[选修 4-1：几何证明选讲] 22．如图，△ABC 的角平分线 AD 的延长线交它的外接圆于点 E． （1）证明：△ABE∽△ADC； （2）若△ABC 的面积 S= AD•AE，求∠BAC 的大小． 　 [选修 4-4：坐标系与参数方程] 23．在直角坐标系 xOy 中，直线 l 的参数方程为 （t 为参数）．在极坐标系 （与直角坐标系 xOy 取相同的长度单位，且以原点 O 为极点，以 x 轴正半轴为极轴）中， 圆 C 的方程为 ρ=2 sinθ． （Ⅰ）求圆 C 的直角坐标方程； （Ⅱ）设圆 C 与直线 l 交于点 A、B，若点 P 的坐标为（3， ），求|PA|+|PB|． 　 [选修 4-5：不等式选讲] 24．例 3．设 a＞0，b＞0，解关于 x 的不等式：|ax﹣2|≥bx． 　 2016 年吉林省实验中学高考数学模拟试卷（理科）（九） 参考答案与试题解析 　 一、选择题：（本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中， 只有一项是符合题目要求的） 1．设集合 A={x|1＜x＜4}，集合 B={x|x2﹣2x﹣3≤0}，则 A∩（∁RB）=（　　） A．（1，4）B．（3，4）C．（1，3）D．（1，2）∪（3，4） 【考点】交、并、补集的混合运算． 【分析】由题意，可先解一元二次不等式，化简集合 B，再求出 B 的补集，再由交的运算 规则解出 A∩（∁RB）即可得出正确选项 【解答】解：由题意 B={x|x2﹣2x﹣3≤0}={x|﹣1≤x≤3}，故∁RB={x|x＜﹣1 或 x＞3}， 又集合 A={x|1＜x＜4}， ∴A∩（∁RB）=（3，4） 故选 B 　 2．已知命题 p：∀x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）≥0，则￢p 是（　　） A．∃x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）≤0B．∀x1，x2∈R，（f（x2）﹣f（x1）） （x2﹣x1）≤0 C．∃x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）＜0D．∀x1，x2∈R，（f（x2）﹣f（x1）） （x2﹣x1）＜0 【考点】命题的否定． 【分析】由题意，命题p 是一个全称命题，把条件中的全称量词改为存在量词，结论的否定 作结论即可得到它的否定，由此规则写出其否定，对照选项即可得出正确选项 【解答】解：命题 p：∀x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）≥0 是一个全称命题，其否 定是一个特称命题， 故¬p：∃x1，x2∈R，（f（x2）﹣f（x1））（x2﹣x1）＜0． 故选：C． 　 3．若复数 z 满足 z（2﹣i）=11+7i（i 为虚数单位），则 z 为（　　） A．3+5iB．3﹣5iC．﹣3+5iD．﹣3﹣5i 【考点】复数代数形式的乘除运算． 【分析】等式两边同乘 2+i，然后化简求出 z 即可． 【解答】解：因为 z（2﹣i）=11+7i（i 为虚数单位）， 所以 z（2﹣i）（2+i）=（11+7i）（2+i）， 即 5z=15+25i， z=3+5i． 故选 A． 　 4．已知{an}是等差数列，公差 d 不为零，前 n 项和是 Sn，若 a3，a4，a8 成等比数列，则（　　） A．a1d＞0，dS4＞0B．a1d＜0，dS4＜0C．a1d＞0，dS4＜0D．a1d＜0，dS4＞0 【考点】等差数列与等比数列的综合． 【分析】由 a3，a4，a8 成等比数列，得到首项和公差的关系，即可判断 a1d 和 dS4 的符号． 【解答】解：设等差数列{an}的首项为 a1，则 a3=a1+2d，a4=a1+3d，a8=a1+7d， 由 a3，a4，a8 成等比数列，得 ，整理得： ． ∵d≠0，∴ ， ∴ ， = ＜0． 故选：B． 　 5．已知 x，y 满足约束条件 ，若 z=ax+y 的最大值为 4，则 a=（　　） A．3B．2C．﹣2D．﹣3 【考点】简单线性规划． 【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定z 的 最大值． 【解答】解：作出不等式组对应的平面区域如图：（阴影部分）． 则 A（2，0），B（1，1）， 若 z=ax+y 过 A 时取得最大值为 4，则 2a=4，解得 a=2， 此时，目标函数为 z=2x+y， 即 y=﹣2x+z， 平移直线 y=﹣2x+z，当直线经过 A（2，0）时，截距最大，此时 z 最大为 4，满足条件， 若 z=ax+y 过 B 时取得最大值为 4，则 a+1=4，解得 a=3， 此时，目标函数为 z=3x+y， 即 y=﹣3x+z， 平移直线 y=﹣3x+z，当直线经过 A（2，0）时，截距最大，此时 z 最大为 6，不满足条件， 故 a=2， 故选：B 　 6．阅读如图所示的程序图，运行相应的程序输出的结果 s=（　　） A．1B．4C．9D．16 【考点】程序框图． 【分析】模拟执行程序，依次写出每次循环得到的 n，s，a 的值，当 n=3 时，不满足条件 n ＜3，退出循环，输出 s 的值为 9． 【解答】解：模拟执行程序框图，可得 a=1，s=0，n=1 s=1，a=3 满足条件 n＜3，n=2，s=4，a=5 满足条件 n＜3，n=3，s=9，a=7 不满足条件 n＜3，退出循环，输出 s 的值为 9， 故选：C． 　 7．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为 n 的样本，其频率分 布直方图如图所示，其中支出在[50，60）元的同学有 30 人，则 n 的值为（　　） A．100B．1000C．90D．900 【考点】用样本的频率分布估计总体分布． 【分析】根据频率直方图的意义，由前三个小组的频率可得样本在[50，60）元的频率，计 算可得样本容量． 【解答】解：由题意可知：前三个小组的频率之和=（0.01+0.024+0.036）×10=0.7， ∴支出在[50，60）元的频率为 1﹣0.7=0.3， ∴n 的值= ； 故选 A． 　 8．关于正态曲线性质的叙述： ①曲线关于直线 x=μ 对称，这个曲线在 x 轴上方； ②曲线关于直线 x=σ 对称，这个曲线只有当 x∈（﹣3σ，3σ）时才在 x 轴上方； ③曲线关于 y 轴对称，因为曲线对应的正态密度函数是一个偶函数； ④曲线在 x=μ 时处于最高点，由这一点向左右两边延伸时，曲线逐渐降低； ⑤曲线的对称轴由 μ 确定，曲线的形状由 σ 确定； ⑥σ 越大，曲线越“矮胖”，σ 越小，曲线越“高瘦”． 上述说法正确的是（　　） A．①④⑤⑥B．②④⑤C．③④⑤⑥D．①⑤⑥ 【考点】正态分布曲线的特点及曲线所表示的意义． 【分析】根据正态曲线的性质，分析选项，即可得出结论． 【解答】解：根据正态曲线的性质，曲线关于直线x=μ 对称，当 x∈（﹣∞，+∞）时，正态 曲线全在 x 轴上方，故①正确，②不正确； 只有当 μ=0 时，正态曲线才关于 y 轴对称，故③不正确； 曲线关于直线 x=μ 对称，曲线在 x=μ 时处于最高点，由这一点向左右两边延伸时，曲线逐 渐降低，故④正确； 曲线的对称轴由 μ 确定，曲线的形状由 σ 确定；σ 越大，曲线越“矮胖”，σ 越小，曲线越“高 瘦”．故⑤⑥正确． 故选：A． 　 9．节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且 都在通电后的 4 秒内任一时刻等可能发生，然后每串彩灯以 4 秒为间隔闪亮，那么这两串彩 灯同时通电后，它们第一次闪亮的时候相差不超过 2 秒的概率是（　　） A． B． C． D． 【考点】几何概型． 【分析】设两串彩灯第一次闪亮的时刻分别为 x，y，由题意可得 0≤x≤4，0≤y≤4，要满足条 件须|x﹣y|≤2，作出其对应的平面区域，由几何概型可得答案． 【解答】解：设两串彩灯第一次闪亮的时刻分别为 x，y， 由题意可得 0≤x≤4，0≤y≤4， 它们第一次闪亮的时候相差不超过 2 秒，则|x﹣y|≤2， 由几何概型可得所求概率为上述两平面区域的面积之比， 由图可知所求的概率为： = 故选 C 　 10．抛物线 y2=4x 的焦点到双曲线 的渐近线的距离是（　　） A． B． C．1D． 【考点】抛物线的简单性质；双曲线的简单性质． 【分析】根据抛物线的标准方程，算出抛物线的焦点 F（1，0）．由双曲线标准方程，算出 它的渐近线方程为 y=± x，化成一般式得： ，再用点到直线的距离公式即可 算出所求距离． 【解答】解：∵抛物线方程为 y2=4x ∴2p=4，可得 =1，抛物线的焦点 F（1，0） 又∵双曲线的方程为 ∴a2=1 且 b2=3，可得 a=1 且 b= ， 双曲线的渐近线方程为 y=± ，即 y=± x， 化成一般式得： ． 因此，抛物线 y2=4x 的焦点到双曲线渐近线的距离为 d= = 故选：B 　 11．若某几何体的三视图（单位：cm）如图所示，则此几何体的体积等于______cm2．（　　） A．16B．18C．24D．26 【考点】由三视图求面积、体积． 【分析】根据三视图得出该几何体是直三棱柱，去掉一个底面相同的三棱锥，求出它的体积 即可． 【解答】解：根据几何体的三视图得： 该几何体是底面为直角三角形，高为 5 的直三棱柱， 去掉一个底面为相同的直角三角形，高为 3 的三棱锥， ∴该几何体的体积为：V 几何体=V 三棱柱﹣V 三棱锥 = ×4×3×5﹣ × ×4×3×3=24 故选：C． 　 12．函数 f（x）= ﹣cosx 在[0，+∞）内 （　　） A．没有零点 B．有且仅有一个零点 C．有且仅有两个零点 D．有无穷多个零点 【考点】函数零点的判定定理． 【分析】根据余弦函数的最大值为 1，可知函数在[π，+∞）上为正值，在此区间上函数没 有零点，问题转化为讨论函数在区间[0，π）上的零点的求解，利用导数讨论单调性即可． 【解答】解：f′（x）= +sinx ①当 x∈[0．π）时， ＞0 且 sinx＞0，故 f′（x）＞0 ∴函数在[0，π）上为单调增 取 x= ＜0，而 ＞0 可得函数在区间（0，π）有唯一零点 ②当 x≥π 时， ＞1 且 cosx≤1 故函数在区间[π，+∞）上恒为正值，没有零点 综上所述，函数在区间[0，+∞）上有唯一零点 　 二、填空题：（本大题共 4 小题，每小题 5 分，共 20 分） 13．已知向量 夹角为 45°，且 ，则 =　3 　． 【考点】平面向量数量积的运算；平面向量数量积的坐标表示、模、夹角． 【分析】由已知可得， = ，代入|2 |= = = = 可求 【解答】解：∵ ， =1 ∴ = ∴|2 |= = = = 解得 故答案为：3 　 14．（1+x）8（1+y）4 的展开式中 x2y2 的系数是　168　． 【考点】二项式系数的性质． 【分析】根据（1+x）8 和（1+y）4 的展开式的通项公式可得 x2y2 的系数． 【解答】解：根据（1+x）8 和（1+y）4 的展开式的通项公式可得，x2y2 的系数为 C82•C42=168， 故答案为：168 　 15． sinxdx=　0　． 【考点】定积分． 【分析】直接根据定积分的计算法则计算即可． 【解答】解： sinxdx=﹣cosx| =0， 故答案为：0 　 16．已知半球内有一内接正方体，则这个半球的表面积与正方体的表面积之比是　3π： 4　． 【考点】球的体积和表面积． 【分析】将半球补成整个的球，同时把原半球的内接正方体再补接一同样的正方体，构成的 长方体刚好是这个球的内接长方体，那么这个长方体的对角线便是它的外接球的直径． 【解答】解：将半球补成整个的球，同时把原半球的内接正方体再补接一同样的正方体，构 成的长方体刚好是这个球的内接长方体，那么这个长方体的对角线便是它的外接球的直径． 设原正方体棱长为 a，球的半径是 R，则根据长方体的对角线性质，得（2R）2=a2+a2+（2a） 2，即 4R2=6a2，∴R=frac{sqrt{6}}{2}a 从而 S 半球的表面积=3πR2= πa2，S 正方体=6a2， 因此 S 半球的表面积：S 正方体=3π：4， 故答案为：3π：4． 　 三、解答题：（本大题共 5 小题，共 70 分．解答应写出说明文字，证明过程或演算步骤） 17．在平面直角坐标系 xOy 中，已知向量 =（ ，﹣ ）， =（sinx，cosx），x∈（0， ）． （1）若 ⊥ ，求 tanx 的值； （2）若 与 的夹角为 ，求 x 的值． 【考点】平面向量数量积的运算；数量积表示两个向量的夹角． 【分析】（1）若 ⊥ ，则 • =0，结合三角函数的关系式即可求 tanx 的值； （2）若 与 的夹角为 ，利用向量的数量积的坐标公式进行求解即可求 x 的值． 【解答】解：（1）若 ⊥ ， 则 • =（ ，﹣ ）•（sinx，cosx）= sinx﹣ cosx=0， 即 sinx= cosx sinx=cosx，即 tanx=1； （2）∵| |= ，| |= =1， • = （ ，﹣ ）•（sinx，cosx）= sinx﹣ cosx， ∴若 与 的夹角为 ， 则 • =| |•| |cos = ， 即 sinx﹣ cosx= ， 则 sin（x﹣ ）= ， ∵x∈（0， ）． ∴x﹣ ∈（﹣ ， ）． 则 x﹣ = 即 x= + = ． 　 18．在一场娱乐晚会上，有 5 位民间歌手（1 至 5 号）登台演唱，由现场数百名观众投票选 出最受欢迎歌手．各位观众须彼此独立地在选票上选 3 名歌手，其中观众甲是 1 号歌手的歌 迷，他必选 1 号，不选 2 号，另在 3 至 5 号中随机选 2 名．观众乙和丙对 5 位歌手的演唱没 有偏爱，因此在 1 至 5 号中随机选 3 名歌手． （Ⅰ） 求观众甲选中 3 号歌手且观众乙未选中 3 号歌手的概率； （Ⅱ） X 表示 3 号歌手得到观众甲、乙、丙的票数之和，求 X 的分布列和数学期望． 【考点】离散型随机变量及其分布列；离散型随机变量的期望与方差． 【分析】（I）设事件 A 表示：“观众甲选中 3 号歌手且观众乙未选中 3 号歌手”，观众甲选中 3 号歌手的概率为 ，观众乙未选中 3 号歌手的概率为 1﹣ = ，利用互斥事件的概率公 式，即可求得结论； （II）由题意，X 可取 0，1，2，3，求出相应的概率，即可得到 X 的分布列与数学期望． 【解答】解：（Ⅰ）设事件 A 表示：“观众甲选中 3 号歌手且观众乙未选中 3 号歌手”， 观众甲选中 3 号歌手的概率为 ，观众乙未选中 3 号歌手的概率为 1﹣ = ， ∴P（A）= ， ∴观众甲选中 3 号歌手且观众乙未选中 3 号歌手的概率为 ； （Ⅱ） X 表示 3 号歌手得到观众甲、乙、丙的票数之和，则 X 可取 0，1，2，3． 观众甲选中 3 号歌手的概率为 ，观众乙选中 3 号歌手的概率为 ， 当观众甲、乙、丙均未选中 3 号歌手时，这时 X=0，P（X=0）=（1﹣ ）（1﹣ ）2= ， 当观众甲、乙、丙只有一人选中 3 号歌手时，这时 X=1， P（X=1）= （1﹣ ）2+（1﹣ ） （1﹣ ）+（1﹣ ）（1﹣ ） = ， 当观众甲、乙、丙只有二人选中 3 号歌手时，这时 X=2， P（X=2）= • （1﹣ ）+（1﹣ ） • + （1﹣ ） = ， 当观众甲、乙、丙都选中 3 号歌手时，这时 X=3， P（X=3）= •（ ）2= ， X 的分布列如下： X 0 1 2 3 P ∴数学期望 EX=0× +1× +2× +3× = ． 　 19．如图，在直三棱柱 A1B1C1﹣ABC 中，AB⊥AC，AB=AC=2，AA1=4，点 D 是 BC 的中 点． （1）求异面直线 A1B 与 C1D 所成角的余弦值； （2）求平面 ADC1 与 ABA1 所成二面角的正弦值． 【考点】与二面角有关的立体几何综合题；异面直线及其所成的角． 【分析】（1）以{ }为单位正交基底建立空间直角坐标系 A﹣xyz，利用向量 法能求出异面直线 A1B 与 C1D 所成角的余弦值． （2）分别求出平面 ABA1 的法向量和平面 ADC1 的法向量，利用向量法能求出平面 ADC1 与 ABA1 所成二面角的余弦值，再由三角函数知识能求出平面 ADC1 与 ABA1 所成二面角的 正弦值． 【解答】解：（1）以{ }为单位正交基底建立空间直角坐标系 A﹣xyz， 则由题意知 A（0，0，0），B（2，0，0），C（0，2，0）， A1（0，0，4），D（1，1，0），C1（0，2，4）， ∴ ， =（1，﹣1，﹣4）， ∴cos＜ ＞= = = ， ∴异面直线 A1B 与 C1D 所成角的余弦值为 ． （2） 是平面 ABA1 的一个法向量， 设平面 ADC1 的法向量为 ， ∵ ， ∴ ，取 z=1，得 y=﹣2，x=2， ∴平面 ADC1 的法向量为 ， 设平面 ADC1 与 ABA1 所成二面角为 θ， ∴cosθ=|cos＜ ＞|=| |= ， ∴sinθ= = ． ∴平面 ADC1 与 ABA1 所成二面角的正弦值为 ． 　 20．如图，点 P（0，﹣1）是椭圆 C1： + =1（a＞b＞0）的一个顶点，C1 的长轴是 圆 C2：x2+y2=4 的直径，l1，l2 是过点 P 且互相垂直的两条直线，其中 l1 交圆 C2 于 A、B 两 点，l2 交椭圆 C1 于另一点 D． （1）求椭圆 C1 的方程； （2）求△ABD 面积的最大值时直线 l1 的方程． 【考点】直线与圆锥曲线的关系；椭圆的标准方程． 【分析】（1）由题意可得 b=1，2a=4，即可得到椭圆的方程； （2）设 A（x1，y1），B（x2，y2），D（x0，y0）．由题意可知：直线 l1 的斜率存在，设为 k， 则直线 l1 的方程为 y=kx﹣1．利用点到直线的距离公式和弦长公式即可得出圆心 O 到直线 l1 的距离和弦长|AB|，又 l2⊥l1，可得直线 l2 的方程为 x+kx+k=0，与椭圆的方程联立即可得 到点 D 的横坐标，即可得出|PD|，即可得到三角形 ABD 的面积，利用基本不等式的性质即 可得出其最大值，即得到 k 的值． 【解答】解：（1）由题意可得 b=1，2a=4，即 a=2． ∴椭圆 C1 的方程为 ； （2）设 A（x1，y1），B（x2，y2），D（x0，y0）． 由题意可知：直线 l1 的斜率存在，设为 k，则直线 l1 的方程为 y=kx﹣1． 又圆 的圆心 O（0，0）到直线 l1 的距离 d= ． ∴|AB|= = ． 又 l2⊥l1，故直线 l2 的方程为 x+ky+k=0，联立 ，消去 y 得到（4+k2） x2+8kx=0，解得 ， ∴|PD|= ． ∴三角形 ABD 的面积 S△= = ， 令 4+k2=t＞4，则 k2=t﹣4， f（t）= = = ， ∴S△= ，当且仅 ，即 ，当 时取等号， 故所求直线 l1 的方程为 ． 　 21．设 x1，x2（x1≠x2）是函数 f（x）=ax3+bx2﹣a2x（a＞0）的两个极值点． （1）若 x1=﹣1，x2=2，求函数 f（x）的解析式； （2）若 ，求 b 的最大值． （3）若 x1＜x＜x2，且 x2=a，g（x）=f'（x）﹣a（x﹣x1），求证： ． 【考点】函数在某点取得极值的条件；函数解析式的求解及常用方法；一元二次方程的根的 分布与系数的关系． 【分析】（1）求导函数，根据 x1=﹣1，x2=2 是函数 f（x）的两个极值点，即可求得函数 f （x）的解析式； （2）根据 x1，x2 是函数 f（x）的两个极值点，可知 x1，x2 是方程 3ax2+2bx﹣a2=0 的两根， 从而 ，利用 ，可得 b2=3a2（6﹣a），令 h（a）=3a2（6﹣a），利用导数，即可求得 b 的最大值； （3）根据 x1，x2 是方程 3ax2+2bx﹣a2=0 的两根，可得 f'（x）=3a（x﹣x1）（x﹣x2），根据 ，可得 ，进而有 = ，利用配方法即可得出结论． 【解答】解：（1）求导函数，可得 f′（x）=3ax2+2bx﹣a2， ∵x1=﹣1，x2=2 是函数 f（x）的两个极值点， ∴f'（﹣1）=0，f'（2）=0， ∴3a﹣2b﹣a2=0，12a+4b﹣a2=0， 解得 a=6，b=﹣9． ∴f（x）=6x3﹣9x2﹣36x．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣ （2）∵x1，x2 是函数 f（x）的两个极值点，∴f'（x1）=f'（x2）=0． ∴x1，x2 是方程 3ax2+2bx﹣a2=0 的两根，故有△=4b2+12a3＞0 对一切 a＞0，b∈R 恒成立． ∴ ， ∵a＞0，∴x1•x2＜0， ∴ ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣ 由 得 ， ∴b2=3a2（6﹣a）． ∵b2≥0，∴3a2（6﹣a）≥0，∴0＜a≤6． 令 h（a）=3a2（6﹣a），则 h′（a）=36a﹣9a2． 当 0＜a＜4 时，h′（a）＞0，∴h（a）在（0，4）内是增函数； 当 4＜a＜6 时，h′（a）＜0，∴h（a）在（0，4）内是减函数； ∴当 a=4 时，h（a）是极大值为 96， ∴h（a）在（0，6）上的最大值是 96，∴b 的最大值是 ．… （3）∵x1，x2 是方程 3ax2+2bx﹣a2=0 的两根．∴f'（x）=3a（x﹣x1）（x﹣x2） ∵ ，∴ ∴ … ∵x1＜x＜x2， ∴ ═ =﹣3a 　 请考生在第 22，23，24 三题中任选一题作答，如果多做，则按所做的第一题计分．[选修 4-1：几何证明选讲] 22．如图，△ABC 的角平分线 AD 的延长线交它的外接圆于点 E． （1）证明：△ABE∽△ADC； （2）若△ABC 的面积 S= AD•AE，求∠BAC 的大小． 【考点】圆內接多边形的性质与判定． 【分析】（1）要判断两个三角形相似，可以根据三角形相似判定定理进行证明，但注意观察 已知条件中给出的是角的关系，故采用判定定理 1 更合适，故需要再找到一组对应角相等， 由圆周角定理，易得满足条件的角． （2）根据（1）的结论，我们可得三角形对应对成比例，由此我们可以将△ABC 的面积 转化为 S= AB•AC，再结合三角形面积公式，不难得到∠BAC 的大小． 【解答】证明：（1）由已知△ABC 的角平分线为 AD， 可得∠BAE=∠CAD 因为∠AEB 与∠ACB 是同弧上的圆周角， 所以∠AEB=∠ACD 故△ABE∽△ADC． 解：（2）因为△ABE∽△ADC， 所以 ， 即 AB•AC=AD•AE． 又 S= AB•ACsin∠BAC， 且 S= AD•AE， 故 AB•ACsin∠BAC=AD•AE． 则 sin∠BAC=1， 又∠BAC 为三角形内角， 所以∠BAC=90°． 　 [选修 4-4：坐标系与参数方程] 23．在直角坐标系 xOy 中，直线 l 的参数方程为 （t 为参数）．在极坐标系 （与直角坐标系 xOy 取相同的长度单位，且以原点 O 为极点，以 x 轴正半轴为极轴）中， 圆 C 的方程为 ρ=2 sinθ． （Ⅰ）求圆 C 的直角坐标方程； （Ⅱ）设圆 C 与直线 l 交于点 A、B，若点 P 的坐标为（3， ），求|PA|+|PB|． 【考点】直线的参数方程；简单曲线的极坐标方程． 【分析】（I）由⊙C 的方程 可得： ，利用极坐标化为直 角坐标的公式 x=ρcosθ，y=ρsinθ 即可得出．． （II）把直线 l 的参数方程 （t 为参数）代入⊙C 的方程得到关于 t 的一元二 次方程，即可得到根与系数的关系，根据参数的意义可得|PA|+|PB|=|t1|+|t2|即可得出． 【解答】解：（I）由⊙C 的方程 可得： ，化为 ． （II）把直线 l 的参数方程 （t 为参数）代入⊙C 的方程得 =0，化为 ． ∴ ．（t1t2=4＞0）． 根据参数的意义可得|PA|+|PB|=|t1|+|t2|=|t1+t2|= ． 　 [选修 4-5：不等式选讲] 24．例 3．设 a＞0，b＞0，解关于 x 的不等式：|ax﹣2|≥bx． 【考点】绝对值不等式． 【分析】首先分析题目由 a＞0，b＞0，解关于 x 的不等式：|ax﹣2|≥bx，去绝对值号得到 ax﹣2≥bx 或 ax﹣2≤﹣bx，对于不等式 ax﹣2≤﹣bx，可直接解得．对于不等式 ax﹣2≥bx，需 要分别讨论当 a＞b＞0 时，当 a=b＞0 时，当 0＜a＜b 时的解集，然后取它们的并集即得到 答案． 【解答】解：原不等式|ax﹣2|≥bx 可化为 ax﹣2≥bx 或 ax﹣2≤﹣bx， （1）对于不等式 ax﹣2≤﹣bx，即（a+b）x≤2 因为 a＞0，b＞0 即： ． （2）对于不等式 ax﹣2≥bx，即（a﹣b）x≥2① 当 a＞b＞0 时，由①得 ，∴此时，原不等式解为： 或 ； 当 a=b＞0 时，由①得 x∈ϕ，∴此时，原不等式解为： ； 当 0＜a＜b 时，由①得 ，∴此时，原不等式解为： ． 综上可得，当 a＞b＞0 时，原不等式解集为 ， 当 0＜a≤b 时，原不等式解集为 ． 　 2016 年 7 月 19 日