江苏省无锡市高考数学一模试卷解析 29页

2017 年江苏省无锡市高考数学一模试卷 　 一.填空题：本大題共 14 小败，每小題 5 分，共 70 分.不需要写出解答过程 1．已知集合 U={1，2，3，4，5，6，7}， M={x|x2﹣6x+5≤0，x∈Z}，则 ∁ UM=　　． 2．若复数 z 满足 z+i= ，其中 i 为虚数单位，则|z|=　　． 3．函数 f（x）= 的定义域为　　． 4．如图是给出的一种算法，则该算法输出的结果是　　 5．某高级中学共有 900 名学生，现用分层抽样的方法从该校学 生中抽取 1 个容 量为 45 的样本，其中高一年级抽 20 人，高三年级抽 10 人，则该校高二年级学 生人数为　　． 6． 已 知 正 四 棱 锥 的 底 面 边 长 是 2， 侧 棱 长 是 ， 则 该 正 四 棱 锥 的 体 积 为　　． 7．从集合{1，2，3，4}中任取两个不同的数，则这两个数的和为 3 的倍数的槪 率为　　． 8．在平面直角坐标系 xOy 中，已知抛物线 y2=8x 的焦点恰好是双曲线 ﹣ =l 的右焦点，则双曲线的离心率为　　． 9．设等比数列{an}的前 n 项和为 Sn，若 S3，S9，S6 成等差数列．且 a2+a5=4，则 a8 的值为　　． 10．在平面直角坐标系 xOy 中，过点 M（1，0）的直线 l 与圆 x2+y2=5 交于 A，B 两点，其中 A 点在第一象限，且 =2 ，则直线 l 的方程为　　． 11．在△ABC 中，已知 AB=1，AC=2，∠A=60°，若点 P 满足 = + ，且 • =1，则实数 λ 的值为　　． 12．已知 sinα=3sin（α+ ），则 tan（α+ ）=　　． 13 ． 若 函 数 f （ x ） = ， 则 函 数 y=|f （ x ） |﹣ 的 零 点 个 数 为　　． 14．若正数 x，y 满足 15x﹣y=22，则 x3+y3﹣x2﹣y2 的最小值为　　． 　 二.解答题：本大题共 6 小题，共计 90 分 15．在△ABC 中，a，b，c 分别为角 A，B，C 的对边．若 acosB=3，bcosA=l，且 A﹣B= （1）求边 c 的长； （2）求角 B 的大小． 16．如图，在斜三梭柱 ABC﹣A1B1C1 中，侧面 AA1C1C 是菱形，AC1 与 A1C 交于点 O，E 是棱 AB 上一点，且 OE∥平面 BCC1B1 （1）求证：E 是 AB 中点； （2）若 AC1⊥A1B，求证：AC1⊥BC． 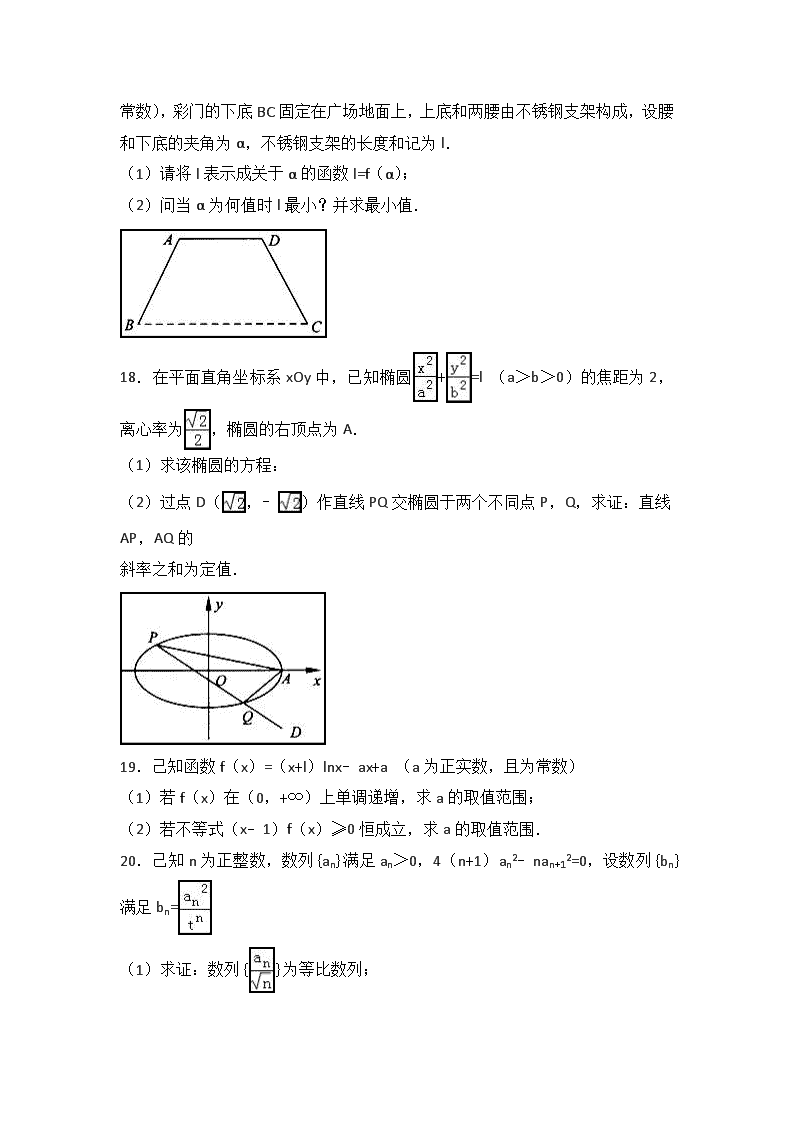17．某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门 BADC （如图），设计要求彩门的面积为 S （单位：m2）•高为 h（单位：m）（S，h 为 常数），彩门的下底 BC 固定在广场地面上，上底和两腰由不锈钢支架构成，设腰 和下底的夹角为 α，不锈钢支架的长度和记为 l． （1）请将 l 表示成关于 α 的函数 l=f（α）； （2）问当 α 为何值时 l 最小？并求最小值． 18．在平面直角坐标系 xOy 中，已知椭圆 + =l （a＞b＞0）的焦距为 2， 离心率为 ，椭圆的右顶点为 A． （1）求该椭圆的方程： （2）过点 D（ ，﹣ ）作直线 PQ 交椭圆于两个不同点 P，Q，求证：直线 AP，AQ 的 斜率之和为定值． 19．己知函数 f（x）=（x+l）lnx﹣ax+a （a 为正实数，且为常数） （1）若 f（x）在（0，+∞）上单调递增，求 a 的取值范围； （2）若不等式（x﹣1）f（x）≥0 恒成立，求 a 的取值范围． 20．己知 n 为正整数，数列{an}满足 an＞0，4（n+1）an2﹣nan+12=0，设数列{bn} 满足 bn= （1）求证：数列{ }为等比数列； （2）若数列{bn}是等差数列，求实数 t 的值： （3）若数列{bn}是等差数列，前 n 项和为 Sn，对任意的 n∈N*，均存在 m∈N*， 使得 8a12Sn﹣a14n2=16bm 成立，求满足条件的所有整数 a1 的值． 　 四.选做题本题包括 A，B，C，D 四个小题，请选做其中两题，若多做，则按作 答的前两题评分．A.[选修 4 一 1：几何证明选讲] 21．如图，圆 O 的直径 AB=6，C 为圆周上一点，BC=3，过 C 作圆的切线 l，过 A 作 l 的垂线 AD，AD 分别与直线 l、圆交于点 D、E．求∠DAC 的度数与线段 AE 的 长． 　 [选修 4-2：矩阵与变换] 22．已知二阶矩阵 M 有特征值 λ=8 及对应的一个特征向量 =[ ]，并且矩阵 M 对应的变换将点（﹣1，2）变换成（﹣2，4）． （1）求矩阵 M； （2）求矩阵 M 的另一个特征值． 　 [选修 4-4：坐标系与参数方程] 23．已知圆 O1 和圆 O2 的极坐标方程分别为 ρ=2， ． （1）把圆 O1 和圆 O2 的极坐标方程化为直角坐标方程； （2）求经过两圆交点的直线的极坐标方程． 　 [选修 4-5：不等式选讲] 24．已知 a，b，c 为正数，且 a+b+c=3，求 + + 的最大值． 　 四.必做题：每小题 0 分，共计 20 分 25．如图，已知正四棱锥 P﹣ABCD 中，PA=AB=2，点 M，N 分别在 PA，BD 上， 且 = = ． （1）求异面直线 MN 与 PC 所成角的大小； （2）求二面角 N﹣PC﹣B 的余弦值． 26．设|θ|＜ ，n 为正整数，数列{an}的通项公式 an=sin tannθ，其前 n 项 和为 Sn （1）求证：当 n 为偶函数时，an=0；当 n 为奇函数时，an=（﹣1） tannθ； （2）求证：对任何正整数 n，S2n= sin2θ•[1+（﹣1）n+1tan2nθ]． 　 2017 年江苏省无锡市高考数学一模试卷 参考答案与试题解析 　 一.填空题：本大題共 14 小败，每小題 5 分，共 70 分.不需要写出解答过程 1．已知集合 U={1，2，3，4，5，6，7}，M={x|x2﹣6x+5≤0，x∈Z}，则∁UM=　 {6，7}　． 【考点】补集及其运算． 【分析】解不等式化简集合 M，根据补集的定义写出运算结果即可． 【解答】解：集合 U={1，2，3，4，5，6，7}， M={x|x2﹣6x+5≤0，x∈Z}={x|1≤x≤5，x∈Z}={1，2，3，4，5}， 则∁UM={6，7}． 故答案为：{6，7}． 　 2．若复数 z 满足 z+i= ，其中 i 为虚数单位，则|z|=　 　． 【考点】复数代数形式的乘除运算． 【分析】直接由复数代数形式的乘除运算化简复数 z，再由复数求模公式计算得 答案． 【解答】解：由 z+i= ， 得 = ， 则|z|= ． 故答案为： ． 　 3．函数 f（x）= 的定义域为　{x|x＞ 且 x≠1}　． 【考点】函数的定义域及其求法． 【分析】根据对数函数的性质以及分母不是 0，得到关于 x 的不等式组，解出即 可． 【解答】解：由题意得： ， 解得：x＞ 且 x≠1， 故函数的定义域是{x|x＞ 且 x≠1}， 故答案为：{x|x＞ 且 x≠1}． 　 4．如图是给出的一种算法，则该算法输出的结果是　24　 【考点】伪代码． 【分析】模拟程序代码的运行过程，可知程序的功能是利用循环结构计算并输出 变量 t 的值， 由于循环变量的初值为 2，终值为 4，步长为 1，故循环体运行只有 3 次，由此 得到答案． 【解答】解：当 i=2 时，满足循环条件，执行循环 t=1×2=2，i=3； 当 i=3 时，满足循环条件，执行循环 t=2×3=6，i=4； 当 i=4 时，满足循环条件，执行循环 t=6×4=24，i=5； 当 i=5 时，不满足循环条件，退出循环，输出 t=24． 故答案为：24． 　 5．某高级中学共有 900 名学生，现用分层抽样的方法从该校学 生中抽取 1 个容 量为 45 的样本，其中高一年级抽 20 人，高三年级抽 10 人，则该校高二年级学 生人数为　300　． 【考点】分层抽样方法． 【分析】用分层抽样的方法抽取一个容量为 45 的样本，根据高一年级抽 20 人， 高三年级抽 10 人，得到高二年级要抽取的人数，根据该高级中学共有 900 名学 生，算出高二年级学生人数． 【解答】解：∵用分层抽样的方法从某校学生中抽取一个容量为 45 的样本， 其中高一年级抽 20 人，高三年级抽 10 人， ∴高二年级要抽取 45﹣20﹣10=15， ∵高级中学共有 900 名学生， ∴每个个体被抽到的概率是 = ∴该校高二年级学生人数为 =300， 故答案为：300． 　 6．已知正四棱锥的底面边长是 2，侧棱长是 ，则该正四棱锥的体积为　 　． 【考点】棱柱、棱锥、棱台的体积． 【分析】正四棱锥 P﹣ABCD 中，AB=2，PA= ，设正四棱锥的高为 PO，连结 AO，求出 PO，由此能求出该正四棱锥的体积． 【解答】解：如图，正四棱锥 P﹣ABCD 中，AB=2，PA= ， 设正四棱锥的高为 PO，连结 AO， 则 AO= AC= ． 在直角三角形 POA 中，PO= = =1． 所以 VP﹣ABCD= •SABCD•PO= ×4×1= ． 故答案为： ． 　 7．从集合{1，2，3，4}中任取两个不同的数，则这两个数的和为 3 的倍数的槪 率为　 　． 【考点】列举法计算基本事件数及事件发生的概率． 【分析】先求出基本事件总数 n= =6，再利用列举法求出这两个数的和为 3 的 倍数包含的基本事件个数，由此能求出这两个数的和为 3 的倍数的槪率． 【解答】解：从集合{1，2，3，4}中任取两个不同的数， 基本事件总数 n= =6， 这两个数的和为 3 的倍数包含的基本事件有：（1，2），（2，4），共 2 个， ∴这两个数的和为 3 的倍数的槪率 p= ． 故答案为： ． 　 8．在平面直角坐标系 xOy 中，已知抛物线 y2=8x 的焦点恰好是双曲线 ﹣ =l 的右焦点，则双曲线的离心率为　2　． 【考点】双曲线的简单性质． 【分析】求得抛物线的焦点坐标，可得 c=2，由双曲线的方程可得 a=1，由离心 率公式可得所求值． 【解答】解：抛物线 y2=8x 的焦点为（2，0）， 则双曲线 ﹣ =l 的右焦点为（2，0）， 即有 c= =2， 不妨设 a=1， 可得双曲线的离心率为 e= =2． 故答案为：2． 　 9．设等比数列{an}的前 n 项和为 Sn，若 S3，S9，S6 成等差数列．且 a2+a5=4，则 a8 的值为　2　． 【考点】等比数列的通项公式． 【 分 析 】 利 用 等 比 数 列 的 前 n 项 和 公 式 和 通 项 公 式 列 出 方 程 组 ， 求 出 ，由此能求出 a8 的值． 【解答】解：∵等比数列{an}的前 n 项和为 Sn，若 S3，S9，S6 成等差数列．且 a2+a5=4， ∴ ， 解得 ， ∴a8= =（a1q）（q3）2=8× =2． 故答案为：2． 　 10．在平面直角坐标系 xOy 中，过点 M（1，0）的直线 l 与圆 x2+y2=5 交于 A，B 两点，其中 A 点在第一象限，且 =2 ，则直线 l 的方程为　x﹣y﹣1=0　． 【考点】直线与圆的位置关系． 【分析】由题意，设直线 x=my+1 与圆 x2+y2=5 联立，利用韦达定理，结合向量 知识，即可得出结论． 【解答】解：由题意，设直线x=my+1 与圆 x2+y2=5 联立，可得（m2+1）y2+2my﹣4=0， 设 A（x1，y1），B（x2，y2），则 y1=﹣2y2，y1+y2=﹣ ，y1y2=﹣ 联立解得 m=1，∴直线 l 的方程为 x﹣y﹣1=0， 故答案为：x﹣y﹣1=0． 　 11．在△ABC 中，已知 AB=1，AC=2，∠A=60°，若点 P 满足 = + ，且 • =1，则实数 λ 的值为　﹣ 或 1　． 【考点】平面向量数量积的运算． 【分析】根据题意，利用平面向量的线性运算，把 、 用 、 与 λ 表示 出来，再求 • 即可． 【解答】解：△ABC 中，AB=1，AC=2，∠A=60°，点 P 满足 = + ， ∴ ﹣ =λ ， ∴ =λ ； 又 = ﹣ =（ +λ ）﹣ = +（λ﹣1） ， ∴ • =λ •[ +（λ﹣1） ] =λ • +λ（λ﹣1） =λ×2×1×cos60°+λ（λ﹣1）×22=1， 整理得 4λ2﹣3λ﹣1=0， 解得 λ=﹣ 或 λ=1， ∴实数 λ 的值为﹣ 或 1． 故答案为：﹣ 或 1． 　 12．已知 sinα=3sin（α+ ），则 tan（α+ ）=　2 ﹣4　． 【考点】两角和与差的正切函数；两角和与差的正弦函数． 【分析】利用同角三角的基本关系、两角和差的三角公式求得tanα、tan 的值， 可得 tan（α+ ）的值． 【解答】解：sinα=3sin（α+ ）=3sinαcos +3cosαsin = sinα+ cosα，∴ tanα= ． 又 tan =tan（ ﹣ ）= = =2﹣ ， ∴ tan （ α+ ） = = = =﹣ =2 ﹣4， 故答案为：2 ﹣4． 　 13．若函数 f（x）= ，则函数 y=|f（x）|﹣ 的零点个数为　 4　． 【考点】根的存在性及根的个数判断． 【分析】利用分段函数，对 x≥1，通过函数的零点与方程根的关系求解零点个 数，当 x＜1 时，利用数形结合求解函数的零点个数即可． 【解答】解：当 x≥1 时， = ，即 lnx= ， 令 g（x）=lnx﹣ ，x≥1 时函数是连续函数， g（1）=﹣ ＜0，g（2）=ln2﹣ =ln ＞0， g（4）=ln4﹣2＜0，由函数的零点判定定理可知 g（x）=lnx﹣ ，有 2 个零 点． （结合函数 y= 与 y= 可知函数的图象由 2 个交点．） 当 x＜1 时，y= ，函数的图象与 y= 的图象如图，考查两个 函数由 2 个交点， 综上函数 y=|f（x）|﹣ 的零点个数为：4 个． 故答案为：4． 　 14．若正数 x，y 满足 15x﹣y=22，则 x3+y3﹣x2﹣y2 的最小值为　1　． 【考点】函数的最值及其几何意义． 【分析】由题意可得 x＞ ，y＞0，又 x3+y3﹣x2﹣y2=（x3﹣x2）+（y3﹣y2），求 出 y3﹣y2≥﹣ y，当且仅当 y= 时取得等号，设 f（x）=x3﹣x2，求出导数和单 调区间、极值和最值，即可得到所求最小值． 【解答】解：由正数x，y 满足 15x﹣y=22，可得 y=15x﹣22＞0，则 x＞ ，y＞ 0， 又 x3+y3﹣x2﹣y2=（x3﹣x2）+（y3﹣y2）， 其中 y3﹣y2+ y=y（y2﹣y+ ）=y（y﹣ ）2≥0， 即 y3﹣y2≥﹣ y， 当且仅当 y= 时取得等号， 设 f（x）=x3﹣x2，f（x）的导数为 f′（x）=3x2﹣2x=x（3x﹣2）， 当 x= 时，f（x）的导数为 ×（ ﹣2）= ， 可得 f（x）在 x= 处的切线方程为 y= x﹣ ． 由 x3﹣x2≥ x﹣ ⇔（x﹣ ）2（x+2）≥0， 当 x= 时，取得等号． 则 x3+y3﹣x2﹣y2=（x3﹣x2）+（y3﹣y2）≥ x﹣ ﹣ y≥ ﹣ =1． 当且仅当 x= ，y= 时，取得最小值 1． 故答案为：1． 　 二.解答题：本大题共 6 小题，共计 90 分 15．在△ABC 中，a，b，c 分别为角 A，B，C 的对边．若 acosB=3，bcosA=l，且 A﹣B= （1）求边 c 的长； （2）求角 B 的大小． 【考点】余弦定理；正弦定理． 【 分 析 】（1 ） 由 acosB=3 ， bcosA=l ， 利 用 余 弦 定 理 化 为 ： a2+c2﹣b2=6c ， b2+c2﹣a2=2c．相加即可得出 c． （2）由（1）可得：a2﹣b2=8．由正弦定理可得： = = ，又 A﹣B= ， 可 得 A=B+ ， C= ， 可 得 sinC=sin ． 代 入 可 得 ﹣16sin2B= ，化简即可得出． 【解答】解：（1）∵acosB=3，bcosA=l，∴a× =3，b× =1， 化为：a2+c2﹣b2=6c，b2+c2﹣a2=2c． 相加可得：2c2=8c，解得 c=4． （2）由（1）可得：a2﹣b2=8． 由正弦定理可得： = = ， 又 A﹣B= ， ∴ A=B+ ， C=π﹣ （ A+B ） = ， 可 得 sinC=sin ． ∴a= ，b= ． ∴ ﹣16sin2B= ， ∴1﹣ ﹣（1﹣cos2B）= ，即 cos2B﹣ = ， ∴﹣2 ═ ， ∴ =0 或 =1，B∈ ． 解得：B= ． 　 16．如图，在斜三梭柱 ABC﹣A1B1C1 中，侧面 AA1C1C 是菱形，AC1 与 A1C 交于点 O，E 是棱 AB 上一点，且 OE∥平面 BCC1B1 （1）求证：E 是 AB 中点； （2）若 AC1⊥A1B，求证：AC1⊥BC． 【考点】空间中直线与直线之间的位置关系；直线与平面平行的性质． 【分析】（1）利用同一法，首先通过连接对角线得到中点，进一步利用中位线， 得到线线平行，进一步利用线面平行的判定定理，得到结论． （2）利用菱形的对角线互相垂直，进一步利用线面垂直的判定定理，得到线面 垂直，最后转化成线线垂直． 【解答】证明：（1）连结 BC1，取 AB 中点 E′， ∵侧面 AA1C1C 是菱形，AC1 与 A1C 交于点 O， ∴O 为 AC1 的中点， ∵E′是 AB 的中点， ∴OE′∥BC1； ∵OE′⊄平面 BCC1B1，BC1⊂平面 BCC1B1， ∴OE′∥平面 BCC1B1， ∵OE∥平面 BCC1B1， ∴E，E′重合， ∴E 是 AB 中点； （2）∵侧面 AA1C1C 是菱形， ∴AC1⊥A1C， ∵AC1⊥A1B，A1C∩A1B=A1，A1C⊂平面 A1BC，A1B⊂平面 A1BC， ∴AC1⊥平面 A1BC， ∵BC⊂平面 A1BC， ∴AC1⊥BC． 　 17．某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门 BADC （如图），设计要求彩门的面积为 S （单位：m2）•高为 h（单位：m）（S，h 为 常数），彩门的下底 BC 固定在广场地面上，上底和两腰由不锈钢支架构成，设腰 和下底的夹角为 α，不锈钢支架的长度和记为 l． （1）请将 l 表示成关于 α 的函数 l=f（α）； （2）问当 α 为何值时 l 最小？并求最小值． 【考点】函数模型的选择与应用． 【分析】（1）求出上底，即可将 l 表示成关于 α 的函数 l=f（α）； （2）求导数，取得函数的单调性，即可解决当 α 为何值时 l 最小？并求最小 值． 【解答】解：（1）设上底长为 a，则 S= ， ∴a= ﹣ ， ∴l= ﹣ + （0＜α＜ ）； （2）l′=h ， ∴0＜α＜ ，l′＜0， ＜α＜ ，l′＞0， ∴ 时，l 取得最小值 m． 　 18．在平面直角坐标系 xOy 中，已知椭圆 + =l （a＞b＞0）的焦距为 2， 离心率为 ，椭圆的右顶点为 A． （1）求该椭圆的方程： （2）过点 D（ ，﹣ ）作直线 PQ 交椭圆于两个不同点 P，Q，求证：直线 AP，AQ 的 斜率之和为定值． 【考点】直线与椭圆的位置关系． 【分析】（1）由题意可知 2c=2，c=1，离心率 e= ，求得 a=2，则 b2=a2﹣c2=1， 即可求得椭圆的方程： （2）则直线 PQ 的方程：y=k（x﹣ ）﹣ ，代入椭圆方程，由韦达定理及直 线的斜率公式，分别求得直线 AP，AQ 的斜率，即可证明直线 AP，AQ 的率之和 为定值． 【解答】解：（1）由题意可知：椭圆 + =l （a＞b＞0），焦点在 x 轴上， 2c=1，c=1， 椭圆的离心率 e= = ，则 a= ，b2=a2﹣c2=1， 则椭圆的标准方程： ； （2）证明：设 P（x1，y1），Q（x2，y2），A（ ，0）， 由题意 PQ 的方程：y=k（x﹣ ）﹣ ， 则 ，整理得：（2k2+1）x2﹣（4 k2+4 k）x+4k2+8k+2=0， 由韦达定理可知：x1+x2= ，x1x2= ， 则 y1+y2=k（x1+x2）﹣2 k﹣2 = ， 则 kAP+kAQ= + = ， 由 y1x2+y2x1=[k（x1﹣ ）﹣ ]x2+[k（x2﹣ ）﹣ ]x1=2kx1x2﹣（ k+ ） （x1+x2）=﹣ ， kAP+kAQ= = =1， ∴直线 AP，AQ 的斜率之和为定值 1． 　 19．己知函数 f（x）=（x+l）lnx﹣ax+a （a 为正实数，且为常数） （1）若 f（x）在（0，+∞）上单调递增，求 a 的取值范围； （2）若不等式（x﹣1）f（x）≥0 恒成立，求 a 的取值范围． 【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性． 【分析】（1）求出函数 f（x）的导数，问题转化为 a≤lnx+ +1 在（0，+∞）恒 成立，（a＞0），令 g（x）=lnx+ +1，（x＞0），根据函数的单调性求出 a 的范围 即可； （2）问题转化为（x﹣1）[（x+1）lnx﹣a]≥0 恒成立，通过讨论 x 的范围，结 合函数的单调性求出 a 的范围即可． 【解答】解：（1）f（x）=（x+l）lnx﹣ax+a，f′（x）=lnx+ +1﹣a， 若 f（x）在（0，+∞）上单调递增， 则 a≤lnx+ +1 在（0，+∞）恒成立，（a＞0）， 令 g（x）=lnx+ +1，（x＞0）， g′（x）= ， 令 g′（x）＞0，解得：x＞1，令 g′（x）＜0，解得：0＜x＜1， 故 g（x）在（0，1）递减，在（1，+∞）递增， 故 g（x）min=g（1）=2， 故 0＜a≤2； （2）若不等式（x﹣1）f（x）≥0 恒成立， 即（x﹣1）[（x+1）lnx﹣a]≥0 恒成立， ①x≥1 时，只需 a≤（x+1）lnx 恒成立， 令 m（x）=（x+1）lnx，（x≥1）， 则 m′（x）=lnx+ +1， 由（1）得：m′（x）≥2， 故 m（x）在[1，+∞）递增，m（x）≥m（1）=0， 故 a≤0，而 a 为正实数，故 a≤0 不合题意； ②0＜x＜1 时，只需 a≥（x+1）lnx， 令 n（x）=（x+1）lnx，（0＜x＜1）， 则 n′（x）=lnx+ +1，由（1）n′（x）在（0，1）递减， 故 n′（x）＞n（1）=2， 故 n（x）在（0，1）递增，故 n（x）＜n（1）=0， 故 a≥0，而 a 为正实数，故 a＞0． 　 20．己知 n 为正整数，数列{an}满足 an＞0，4（n+1）an2﹣nan+12=0，设数列{bn} 满足 bn= （1）求证：数列{ }为等比数列； （2）若数列{bn}是等差数列，求实数 t 的值： （3）若数列{bn}是等差数列，前 n 项和为 Sn，对任意的 n∈N*，均存在 m∈N*， 使得 8a12Sn﹣a14n2=16bm 成立，求满足条件的所有整数 a1 的值． 【考点】数列的求和；等比数列的通项公式． 【分析】（1）数列{an}满足 an＞0，4（n+1）an2﹣nan+12=0，化为： =2× ，即可证明． （2）由（1）可得： = ，可得 =n •4n﹣1 ．数列{bn}满足 bn= ，可得 b1，b2，b3，利用数列{bn}是等差数列即可得出 t． （3）根据（2）的结果分情况讨论 t 的值，化简 8a12Sn﹣a14n2=16bm，即可得出 a1． 【解答】（1）证明：数列{an}满足 an＞0，4（n+1）an2﹣nan+12=0， ∴ = an+1，即 =2 ， ∴数列{ }是以 a1 为首项，以 2 为公比的等比数列． （2）解：由（1）可得： = ，∴ =n •4n﹣1． ∵bn= ，∴b1= ，b2= ，b3= ， ∵数列{bn}是等差数列，∴2× = + ， ∴ = + ， 化为：16t=t2+48，解得 t=12 或 4． （3）解：数列{bn}是等差数列，由（2）可得：t=12 或 4． ①t=12 时，bn= = ，Sn= ， ∵对任意的 n∈N*，均存在 m∈N*，使得 8a12Sn﹣a14n2=16bm 成立， ∴ × ﹣a14n2=16× ， ∴ = ，n=1 时，化为：﹣ = ＞0，无解，舍去． ②t=4 时，bn= = ，Sn= ， 对任意的 n∈N*，均存在 m∈N*，使得 8a12Sn﹣a14n2=16bm 成立， ∴ × ﹣a14n2=16× ， ∴n =4m， ∴a1= ．∵a1 为正整数，∴ = k，k∈N*． ∴满足条件的所有整数 a1 的值为{a1|a1=2 ，n∈N*，m∈N*，且 = k，k∈ N*}． 　 四.选做题本题包括 A，B，C，D 四个小题，请选做其中两题，若多做，则按作 答的前两题评分．A.[选修 4 一 1：几何证明选讲] 21．如图，圆 O 的直径 AB=6，C 为圆周上一点，BC=3，过 C 作圆的切线 l，过 A 作 l 的垂线 AD，AD 分别与直线 l、圆交于点 D、E．求∠DAC 的度数与线段 AE 的 长． 【考点】弦切角． 【分析】连接 OC，先证得三角形 OBC 是等边三角形，从而得到∠DCA=60°，再 在直角三角形 ACD 中得到∠DAC 的大小；考虑到直角三角形 ABE 中，利用角的 关系即可求得边 AE 的长． 【解答】解：如图，连接 OC，因 BC=OB=OC=3， 因此∠CBO=60°，由于∠DCA=∠CBO， 所以∠DCA=60°，又 AD⊥DC 得∠DAC=30°； 又因为∠ACB=90°， 得∠CAB=30°，那么∠EAB=60°， 从而∠ABE=30°， 于是 ． 　 [选修 4-2：矩阵与变换] 22．已知二阶矩阵 M 有特征值 λ=8 及对应的一个特征向量 =[ ]，并且矩阵 M 对应的变换将点（﹣1，2）变换成（﹣2，4）． （1）求矩阵 M； （2）求矩阵 M 的另一个特征值． 【考点】特征值与特征向量的计算；几种特殊的矩阵变换． 【分析】（1）先设矩阵 A= ，这里 a，b，c，d∈R，由二阶矩阵 M 有特征值 λ=8 及对应的一个特征向量 e1 及矩阵 M 对应的变换将点（﹣1，2）换成（﹣2， 4）．得到关于 a，b，c，d 的方程组，即可求得矩阵 M； （2）由（1）知，矩阵 M 的特征多项式为 f（λ）=（λ﹣6）（λ﹣4）﹣8=λ2﹣10λ+16， 从而求得另一个特征值为 2． 【解答】解：（1）设矩阵 A= ，这里 a，b，c，d∈R， 则 =8 = ， 故 ， 由于矩阵 M 对应的变换将点（﹣1，2）换成（﹣2，4）． 则 = ， 故 联立以上两方程组解得 a=6，b=2，c=4，d=4，故 M= ． （2）由（1）知，矩阵 M 的特征多项式为 f（λ）=（λ﹣6）（λ﹣4）﹣8=λ2﹣10λ+16， 故矩阵 M 的另一个特征值为 2． 　 [选修 4-4：坐标系与参数方程] 23．已知圆 O1 和圆 O2 的极坐标方程分别为 ρ=2， ． （1）把圆 O1 和圆 O2 的极坐标方程化为直角坐标方程； （2）求经过两圆交点的直线的极坐标方程． 【考点】简单曲线的极坐标方程；相交弦所在直线的方程． 【分析】（1）先利用三角函数的差角公式展开圆 O2 的极坐标方程的右式，再利 用直角坐标与极坐标间的关系，即利用 ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即 得圆 O2 的直角坐标方程及圆 O1 直角坐标方程． （2）先在直角坐标系中算出经过两圆交点的直线方程，再利用直角坐标与极坐 标间的关系求出其极坐标方程即可． 【解答】解：（1）ρ=2⇒ρ2=4，所以 x2+y2=4；因为 ， 所以 ，所以 x2+y2﹣2x﹣2y﹣2=0． （2）将两圆的直角坐标方程相减，得经过两圆交点的直线方程为 x+y=1． 化为极坐标方程为 ρcosθ+ρsinθ=1，即 ． 　 [选修 4-5：不等式选讲] 24．已知 a，b，c 为正数，且 a+b+c=3，求 + + 的最大值． 【考点】二维形式的柯西不等式． 【分析】利用柯西不等式，结合 a+b+c=3，即可求得 + + 的最 大值． 【解答】解：由柯西不等式可得 （ + + ）2≤[12+12+12][（ ）2+（ ）2+（ ） 2]=3×12 ∴ + + ≤3 ，当且仅当 = = 时取等号． ∴ + + 的最大值是 6， 故最大值为 6． 　 四.必做题：每小题 0 分，共计 20 分 25．如图，已知正四棱锥 P﹣ABCD 中，PA=AB=2，点 M，N 分别在 PA，BD 上， 且 = = ． （1）求异面直线 MN 与 PC 所成角的大小； （2）求二面角 N﹣PC﹣B 的余弦值． 【考点】二面角的平面角及求法；异面直线及其所成的角． 【分析】（1）设 AC 与 BD 的交点为 O，AB=PA=2．以点 O 为坐标原点， ， ， 方向分别是 x 轴、y 轴、z 轴正方向，建立空间直角坐标系 O﹣xyz．利 用向量法能求出异面直线 MN 与 PC 所成角． （2）求出平面 PBC 的法向量和平面 PNC 的法向量，利用向量法能求出二面角 N﹣PC﹣B 的余弦值． 【解答】解：（1）设 AC 与 BD 的交点为 O，AB=PA=2．以点 O 为坐标原点， ， ， 方向分别是 x 轴、y 轴、z 轴正方向，建立空间直角坐标系 O﹣xyz． 则 A（1，﹣1，0），B（1，1，0），C（﹣1，1，0），D（﹣1，﹣1，0），… 设 P（0，0，p），则 =（﹣1，1，p），又 AP=2， ∴1+1+p2=4，∴p= ， ∵ = = =（ ）， =（ ）， ∴ =（﹣1，1，﹣ ）， =（0， ，﹣ ）， 设异面直线 MN 与 PC 所成角为 θ， 则 cosθ= = = ． θ=30°， ∴异面直线 MN 与 PC 所成角为 30°． （2） =（﹣1，1，﹣ ）， =（1，1，﹣ ）， =（ ，﹣ ）， 设平面 PBC 的法向量 =（x，y，z）， 则 ，取 z=1，得 =（0， ，1）， 设平面 PNC 的法向量 =（a，b，c）， 则 ，取 c=1，得 =（ ，2 ，1）， 设二面角 N﹣PC﹣B 的平面角为 θ， 则 cosθ= = = ． ∴二面角 N﹣PC﹣B 的余弦值为 ． 　 26．设|θ|＜ ，n 为正整数，数列{an}的通项公式 an=sin tannθ，其前 n 项 和为 Sn （1）求证：当 n 为偶函数时，an=0；当 n 为奇函数时，an=（﹣1） tannθ； （2）求证：对任何正整数 n，S2n= sin2θ•[1+（﹣1）n+1tan2nθ]． 【考点】数列的求和． 【分析】（1）利用 sin = ，即可得出． （2）a2k﹣1+a2k=（﹣1） tannθ．利用等比数列的求和公式即可得出． 【解答】证明：（1）an=sin tannθ， 当 n=2k（k∈N*）为偶数时，an=sinkπ•tannθ=0； 当 n=2k﹣1 为奇函数时，an= •tannθ=（﹣1）k﹣1tannθ=（﹣1） tannθ． （2）a2k﹣1+a2k=（﹣1） tannθ．∴奇数项成等比数列，首项为 tanθ，公比为 ﹣tan2θ． ∴S2n= = sin2θ•[1+（﹣1）n+1tan2nθ]． 　 2017 年 4 月 18 日