近五年安徽文科高考数学试卷及答案2 49页

‎2007年普通高等学校招生全国统一考试（安徽卷）‎ 数学（文科）‎ 本试卷分第I卷（选择题）和第II卷（非选择题）两部分，第I卷第I至第2页，第II卷第3至第4页．全卷满分150分，考试时间120分钟．‎ 考生注意事项：‎ ‎1．答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致．‎ ‎2．答第I卷时，每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．‎ ‎3．答第II卷时，必须用毫米黑色黑水签字笔在答题卡上书写．在试题卷上作答无效．‎ ‎4．考试结束，监考员将试题和答题卡一并收回．‎ 参考公式：‎ 如果事件互斥，那么 球的表面积公式 ‎ ‎ 如果事件相互独立，那么 球的体积公式 ‎ ‎ ‎ 其中表示球的半径 第I卷（选择题共55分）‎ 一、选择题：本大题共11小题，每小题5分，共55分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．若，，则（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎2．椭圆的离心率为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎3．等差数列的前项和为，若，，则（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎4．下列函数中，反函数是其自身的函数为（　　）‎ Ａ．， Ｂ．‎ Ｃ． Ｄ．，‎ ‎5．若圆的圆心到直线的距离为，则的值为（　　）‎ Ａ．或 Ｂ．或 Ｃ．或 Ｄ．或 ‎6．设，，均为直线，其中在平面内，则“”是“且”的（　　）‎ Ａ．充分不必要条件 Ｂ．必要不充分条件 ‎1‎ ‎2‎ 第7题图 Ｃ．充分必要条件 Ｄ．既不充分也不必要条件 ‎7．图中的图象所表示的函数的解析式为（　　）‎ Ａ．　　　 ‎ Ｂ．　 ‎ Ｃ． ‎ Ｄ． ‎ ‎8．设，且，，，则的大小关系为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎9．如果点在平面区域上，点在曲线上，那么的最小值为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎10．把边长为的正方形沿对角线折成直二面角，折成直二面角后，在四点所在的球面上，与两点之间的球面距离为（　　）‎ Ａ． Ｃ． Ｂ． Ｄ．‎ ‎11．定义在上的函数既是奇函数，又是周期函数，是它的一个正周期．若将方程在闭区间上的根的个数记为，则可能为（　　）‎ Ａ．0 Ｂ．1 Ｃ．3 Ｄ．5‎ ‎2007年普通高等学校招生全国统一考试（安微卷）‎ 数学（文科）‎ 第II卷（非选择题共95分）‎ 注意事项：‎ ‎ 请用毫米黑色墨水签字笔在答题卡上书写作答，在试题卷上书写作答无效 二、填空题：本大题共4小题，每小题4分，共16分，把答案填在答题卡的相应位置．‎ ‎12．已知，则的值等于 ．‎ ‎13．在四面体中，，，，为的中点，为的中点，则 （用表示）‎ ‎14．在正方体上任意选择两条棱，则这两条棱相互平行的概率为 ．‎ ‎15．函数的图象为，如下结论中正确的是 （写出所有正确结论的编号）．‎ ‎①图象关于直线对称；‎ ‎②图象关于点对称；‎ ‎③函数在区间内是增函数；‎ ‎④由的图角向右平移个单位长度可以得到图象．‎ 三、解答题：本大题共6小题，共79分．解答应写出文字说明、证明过程或演算步骤．‎ A B C D ‎16．（本小题满分10分）‎ 解不等式．‎ ‎17．（本小题满分14分）‎ 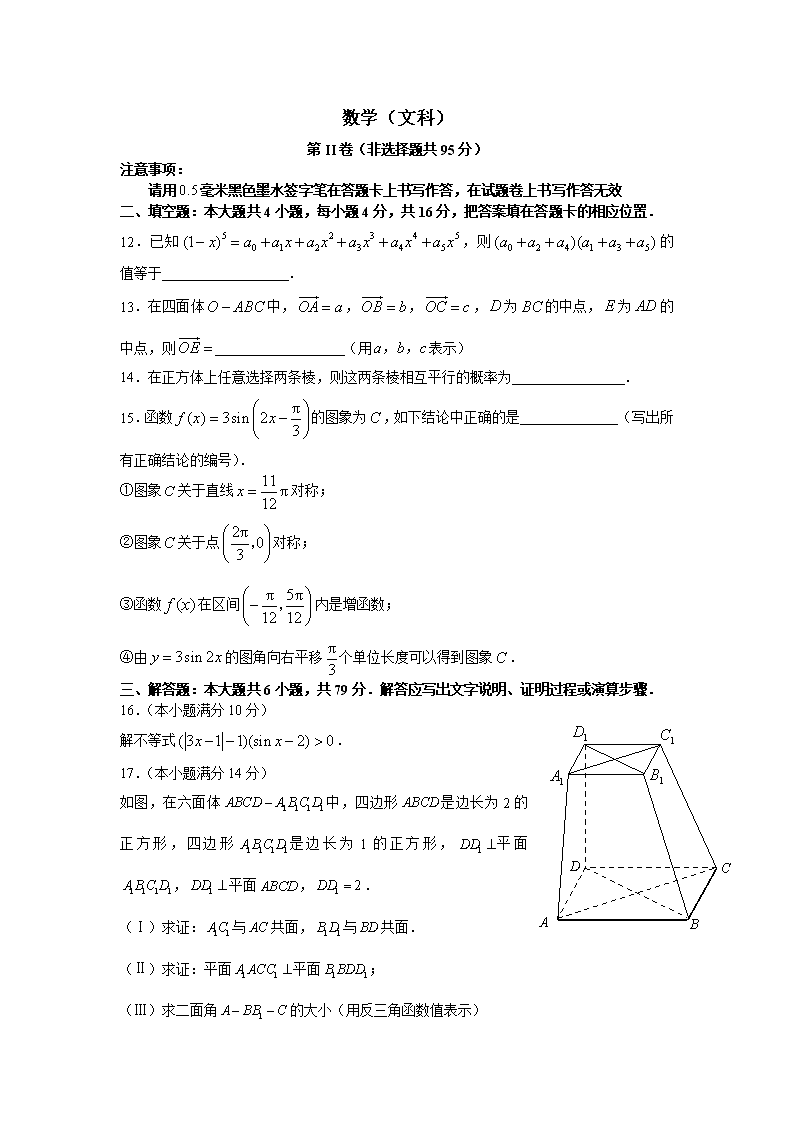如图，在六面体中，四边形是边长为2的正方形，四边形是边长为1的正方形，平面，平面，．‎ ‎（Ⅰ）求证：与共面，与共面．‎ ‎（Ⅱ）求证：平面平面；‎ ‎（Ⅲ）求二面角的大小（用反三角函数值表示）‎ ‎18．（本小题满分14分）‎ 设是抛物线的焦点．‎ ‎（I）过点作抛物线的切线，求切线方程；‎ ‎（II）设为抛物线上异于原点的两点，且满足，延长，分别交抛物线于点，求四边形面积的最小值．‎ ‎19．（本小题满分13分）‎ 在医学生物试验中，经常以果蝇作为试验对象．一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔．‎ ‎（I）求笼内恰好剩下1只果蝇的概率；‎ ‎（II）求笼内至少剩下5只果蝇的概率．‎ ‎20．（本小题满分14分）‎ 设函数，，‎ 其中，将的最小值记为．‎ ‎（I）求的表达式；‎ ‎（II）讨论在区间内的单调性并求极值．‎ ‎21．（本小题满分14分）‎ 某国采用养老储备金制度．公民在就业的第一年就交纳养老储备金，数目为，以后每年交纳的数目均比上一年增加，因此，历年所交纳的储备金数目是一个公差为的等差数列．与此同时，国家给予优惠的计息政策，不仅采用固定利率，而且计算复利．这就是说，如果固定年利率为，那么，在第年末，第一年所交纳的储备金就变为，第二年所交纳的储备金就变为，．以表示到第年末所累计的储备金总额．‎ ‎（Ⅰ）写出与的递推关系式；‎ ‎（Ⅱ）求证：，其中是一个等比数列，是一个等差数列．‎ ‎2007年普通高等学校招生全国统一考试（安徽卷）‎ 数学（文史）参考答案 一、选择题：本题考查基本知识的基本运算．每小题5分，满分55分．‎ ‎1．Ｄ 2．Ａ 3．Ｃ 4．Ｄ 5．Ｃ 6．Ａ ‎ ‎7．Ｂ 8．Ｂ 9．Ａ 10．Ｃ 11．Ｄ 二、填空题：本题考查基本知识和基本运算．每小题4分，满分16分．‎ ‎12． 13． 14． 15．①②③‎ 三、解答题 ‎16．本小题主要考查三角函数的基本性质，含绝对值不等式的解法，考查基本运算能力．本小题满分10分．‎ 解：因为对任意，，所以原不等式等价于．‎ 即，，，故解为．‎ 所以原不等式的解集为．‎ ‎17．本小题主要考查直线与平面的位置关系、平面与平面的位置关系、二面角及其平面角等有关知识，考查空间想象能力和思维能力，应用向量知识解决立体几何问题的能力．本小题满分14分．‎ 解法1（向量法）：‎ A B C D 以为原点，以所在直线分别为轴，轴，轴建立空间直角坐标系如图，‎ 则有．‎ ‎（Ⅰ）证明：．‎ ‎．‎ 与平行，与平行，‎ 于是与共面，与共面．‎ ‎（Ⅱ）证明：，，‎ ‎，．‎ 与是平面内的两条相交直线．‎ 平面．‎ 又平面过．‎ 平面平面．‎ ‎（Ⅲ）解：．‎ 设为平面的法向量，‎ ‎，．‎ 于是，取，则，．‎ 设为平面的法向量，‎ ‎，．‎ 于是，取，则，．‎ A B C D ‎．‎ 二面角的大小为．‎ 解法2（综合法）：‎ ‎（Ⅰ）证明：平面，平面．‎ ‎，，平面平面．‎ 于是，．‎ 设分别为的中点，连结，‎ 有．‎ ‎，‎ 于是．‎ 由，得，‎ 故，与共面．‎ 过点作平面于点，‎ 则，连结，‎ 于是，，．‎ ‎，．‎ ‎，．‎ 所以点在上，故与共面．‎ ‎（Ⅱ）证明：平面，，‎ 又（正方形的对角线互相垂直），‎ 与是平面内的两条相交直线，‎ 平面．‎ 又平面过，平面平面．‎ ‎（Ⅲ）解：直线是直线在平面上的射影，，‎ 根据三垂线定理，有．‎ 过点在平面内作于，连结，‎ 则平面，‎ 于是，‎ 所以，是二面角的一个平面角．‎ 根据勾股定理，有．‎ ‎，有，，，．‎ ‎，，‎ 二面角的大小为．‎ ‎18．本小题主要考查抛物线的方程与性质，抛物线的切点与焦点，向量的数量积，直线与抛物线的位置关系，平均不等式等基础知识，考查综合分析问题、解决问题的能力．本小题满分14分．‎ 解：（I）设切点．由，知抛物线在点处的切线斜率为，故所求切线方程为．‎ 即．‎ 因为点在切线上．‎ 所以，，．‎ 所求切线方程为．‎ ‎（II）设，．‎ 由题意知，直线的斜率存在，由对称性，不妨设．‎ 因直线过焦点，所以直线的方程为．‎ 点的坐标满足方程组 得，‎ 由根与系数的关系知 ‎．‎ 因为，所以的斜率为，从而的方程为．‎ 同理可求得．‎ ‎．‎ 当时，等号成立．所以，四边形面积的最小值为．‎ ‎19．本小题主要考查排列、组合知识与等可能事件、互斥事件概率的计算，运用概率知识分析问题及解决实际问题的能力．本小题满分13分．‎ 解：以表示恰剩下只果蝇的事件．‎ 以表示至少剩下只果蝇的事件．‎ 可以有多种不同的计算的方法．‎ 方法1（组合模式）：当事件发生时，第只飞出的蝇子是苍蝇，且在前只飞出的蝇子中有1只是苍蝇，所以．‎ 方法2（排列模式）：当事件发生时，共飞走只蝇子，其中第只飞出的蝇子是苍蝇，哪一只？有两种不同可能．在前只飞出的蝇子中有只是果蝇，有种不同的选择可能，还需考虑这只蝇子的排列顺序．所以．‎ 由上式立得；‎ ‎．‎ ‎20．本小题主要考查同角三角函数的基本关系，倍角的正弦公式，正弦函数的值域，多项式函数的导数，函数的单调性，考查应用导数分析解决多项式函数的单调区间，极值与最值等问题的综合能力．本小题满分14分．‎ 解：（I）我们有 ‎ ‎ ‎ ‎ ‎ ．‎ 由于，，故当时，达到其最小值，即 ‎．‎ ‎ （II）我们有．‎ 列表如下：‎ 极大值 极小值 由此可见，在区间和单调增加，在区间单调减小，极小值为，极大值为．‎ ‎21．本小题主要考查等差数列、等比数列的基本概念和基本方法，考查学生阅读资料、提取信息、建立数学模型的能力、考查应用所学知识分析和解决实际问题的能力．本小题满分14分．‎ 解：（Ⅰ）我们有．‎ ‎（Ⅱ），对反复使用上述关系式，得 ‎ ， ①‎ 在①式两端同乘，得 ‎ ②‎ ‎②①，得 ‎ ．‎ 即．‎ 如果记，，‎ 则．‎ 其中是以为首项，以为公比的等比数列；是以 为首项，为公差的等差数列．‎ ‎2008年普通高等学校招生全国统一考试（安徽卷）‎ 数 学（文科）‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至第2页，第Ⅱ卷第3至第4页．全卷满分150分，考试时间120分钟．‎ 考生注意事项：‎ 1． 答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致．‎ 2． 答第Ⅰ卷时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．‎ 3． 答第Ⅱ卷时，必须用0.5毫米黑色墨水签字笔在答题卡上书写．在试题卷上作答无效．‎ 4． 考试结束，监考员将试题卷和答题卡一并收回．‎ 参考公式：‎ 如果事件互斥，那么 球的表面积公式 ‎ ‎ 其中表示球的半径 如果事件相互独立，那么 球的体积公式 ‎ ‎ 其中表示球的半径 ‎ ‎ ‎ 第I卷（选择题共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎（1）．若为位全体正实数的集合，则下列结论正确的是（ ）‎ A． B． ‎ C． D． ‎ 解：是全体非正数的集合即负数和0，所以 ‎（2）．若，, 则（ ）‎ A． （1，1） B．（－1，－1） C．（3，7） D．（-3,-7） ‎ 解：向量基本运算 ‎ ‎（3）．已知是两条不同直线，是三个不同平面，下列命题中正确的是（ ）‎ A． B． ‎ C． D． ‎ 解：定理：垂直于一个平面的两条直线互相平行，故选B。‎ ‎（4）．是方程至少有一个负数根的（ ）‎ A．必要不充分条件 B．充分不必要条件 C．充分必要条件 D．既不充分也不必要条件 解：当，得a<1时方程有根。a<0时，，方程有负根，又a=1时，方程根为，所以选B ‎（5）．在三角形中，,则的大小为（ ）‎ A． B． C． D．‎ 解：由余弦定理，‎ ‎（6）．函数的反函数为 A． B． ‎ C． D． ‎ 解：由原函数定义域是反函数的值域，，排除B,D两个；又原函数不能取1，‎ ‎ 不能取1，故反函数定义域不包括1，选C .(直接求解也容易)‎ ‎（7）．设则中奇数的个数为（ ）‎ A．2 B．3 C．4 D．5‎ 解：由题知，逐个验证知，其它为偶数，选A。‎ ‎（8）．函数图像的对称轴方程可能是（ ）‎ A． B． C． D．‎ 解：的对称轴方程为，即，‎ ‎（9）．设函数 则（ ）‎ A．有最大值 B．有最小值 C．是增函数 D．是减函数 解：，，由基本不等式 有最大值，选A ‎（10）若过点的直线与曲线有公共点，则直线的斜率的取值范围为（ ）A． B． C． D．‎ 解：解：设直线方程为，即，直线与曲线有公共点，‎ 圆心到直线的距离小于等于半径 ，‎ 得，选择C 另外，数形结合画出图形也可以判断C正确。‎ ‎（11） 若为不等式组表示的平面区域，则当从－2连续变化到1时，动直线 扫过中的那部分区域的面积为 ( )A． B．1 C． D．5‎ 解：如图知区域的面积是△OAB去掉一个小直角三角形。‎ ‎（阴影部分面积比1大，比小,故选C,不需要算出来） ‎ ‎（12）12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排，若其他人的相对顺序不变，则不同调整方法的总数是 ( )‎ A． B． C． D． ‎ 解：从后排8人中选2人共种选法，这2人插入前排4‎ 人中且保证前排人的顺序不变，则先从4人中的5个空挡插入一人，有5种插法；余下的一人则要插入前排5人的空挡，有6种插法，故为；综上知选C。‎ ‎2008年普通高等学校招生全国统一考试（安徽卷）‎ 数 学（文科）‎ 第Ⅱ卷（非选择题 共90分）‎ 考生注意事项：‎ ‎ 请用0.5毫米黑色墨水签字笔在答题卡上书写作答，在试题卷上书写作答无效．‎ 二、填空题：本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．‎ ‎（13）．函数的定义域为 ．‎ 解：由题知：；解得：x≥3.‎ ‎（14）．已知双曲线的离心率是。则＝ ‎ 解：，离心率，所以 ‎（15） 在数列在中，，，,其中为常数，‎ 则 ‎ 解：∵∴从而。‎ ‎∴a=2，，则 ‎（16）已知点在同一个球面上,若,则两点间的球面距离是 ‎ 解：如图，易得，，，则此球内接长方体三条棱长为AB、BC、CD（CD的对边与CD等长），从而球外接圆的直径为，R=4则BC与球心构成的大圆如图，因为△OBC为正三角形，则B，C两点间的球面距离是。‎ 三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．‎ ‎（17）．（本小题满分12分）‎ 已知函数 ‎（Ⅰ）求函数的最小正周期和图象的对称轴方程 ‎（Ⅱ）求函数在区间上的值域 解：（1）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎（2）‎ 因为在区间上单调递增，在区间上单调递减，‎ 所以 当时，取最大值 1‎ 又 ，当时，取最小值 所以 函数 在区间上的值域为 ‎（18）．（本小题满分12分）‎ ‎ 在某次普通话测试中，为测试汉字发音水平，设置了10张卡片，每张卡片印有一个汉字的拼音，其中恰有3张卡片上的拼音带有后鼻音“g”.‎ ‎（Ⅰ）现对三位被测试者先后进行测试，第一位被测试者从这10张卡片总随机抽取1张，测试后放回，余下2位的测试，也按同样的方法进行。求这三位被测试者抽取的卡片上，拼音都带有后鼻音“g”的概率。‎ ‎（Ⅱ）若某位被测试者从10张卡片中一次随机抽取3张，求这三张卡片上，拼音带有后鼻音“g”的卡片不少于2张的概率。‎ 解：（1）每次测试中，被测试者从10张卡片中随机抽取1张卡片上，拼音带有后鼻音 ‎“g”的概率为，因为三位被测试者分别随机抽取一张卡片的事件是相互独立的，因而所求的概率为 ‎（2）设表示所抽取的三张卡片中，恰有张卡片带有后鼻音“g”的事件，且其相应的概率为则 ‎ , ‎ ‎ 因而所求概率为 ‎ ‎ ‎（19）．（本小题满分12分 如图，在四棱锥中，底面四边长为1的 菱形，, , ,为的中点。‎ ‎（Ⅰ）求异面直线AB与MD所成角的大小；‎ ‎（Ⅱ）求点B到平面OCD的距离。‎ 解：方法一（综合法）‎ ‎（1）‎ ‎ 为异面直线与所成的角（或其补角）‎ ‎ 作连接 ‎ ‎ ‎ ‎ ‎ ，‎ ‎ 所以 与所成角的大小为 ‎（２）点A和点B到平面OCD的距离相等，‎ 连接OP,过点A作 于点Q，‎ ‎ 又 ,线段AQ的长就是点A到平面OCD的距离 ‎ ，‎ ‎ ，所以点B到平面OCD的距离为 方法二(向量法)‎ 作于点P,如图,分别以AB,AP,AO所在直线为轴建立坐标系 ‎,‎ ‎(1)设与所成的角为,‎ ‎ , ‎ 与所成角的大小为 ‎(2) ‎ 设平面OCD的法向量为,则 即 ‎ 取,解得 设点B到平面OCD的距离为,则为在向量上的投影的绝对值,‎ ‎ , .‎ 所以点B到平面OCD的距离为 ‎（20）．（本小题满分12分）‎ 设函数为实数。‎ ‎（Ⅰ）已知函数在处取得极值，求的值； ‎ ‎（Ⅱ）已知不等式对任意都成立，求实数的取值范围。‎ 解: (1)，由于函数在时取得极值，所以 ‎ ‎ 即 ‎ ‎ (2) 方法一 ‎ 由题设知：对任意都成立 ‎ 即对任意都成立 ‎ 设 , 则对任意，为单调递增函数 ‎ 所以对任意，恒成立的充分必要条件是 ‎ 即 ，， 于是的取值范围是 ‎ 方法二 ‎ 由题设知：对任意都成立 ‎ 即对任意都成立 ‎ 于是对任意都成立，即 ‎， 于是的取值范围是 ‎（21）．（本小题满分12分）‎ 设数列满足其中为实数，且 ‎（Ⅰ）求数列的通项公式 ‎（Ⅱ）设，,求数列的前项和；‎ ‎（Ⅲ）若对任意成立，证明 解 (1) 方法一：‎ ‎ ‎ ‎ 当时，是首项为，公比为的等比数列。‎ ‎ ，即 。当时，仍满足上式。‎ ‎ 数列的通项公式为 。‎ 方法二 由题设得：当时，‎ 时，也满足上式。‎ 数列的通项公式为 。‎ ‎ (2) 由（1）得 ‎ ‎ ‎ ‎ (3) 由（1）知 若，则 ‎ ‎ 由对任意成立，知。下面证，用反证法 方法一：假设，由函数的函数图象知，当趋于无穷大时，趋于无穷大 不能对恒成立，导致矛盾。。‎ 方法二：假设，，‎ 即 恒成立 （＊）‎ 为常数， （＊）式对不能恒成立，导致矛盾，‎ ‎（22）．（本小题满分14分）‎ 设椭圆其相应于焦点的准线方程为.‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）已知过点倾斜角为的直线交椭圆于两点，求证：‎ ‎ ;‎ ‎ （Ⅲ）过点作两条互相垂直的直线分别交椭圆于和,求 ‎ 的最小值 解 ：（1）由题意得：‎ ‎ ‎ ‎ 椭圆的方程为 ‎ (2)方法一：‎ ‎ 由（1）知是椭圆的左焦点，离心率 ‎ 设为椭圆的左准线。则 ‎ 作，与轴交于点H(如图)‎ ‎ 点A在椭圆上 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 同理 ‎ ‎ 。‎ 方法二：‎ ‎ 当时，记，则 ‎ 将其代入方程 得 ‎ ‎ 设 ，则是此二次方程的两个根.‎ ‎ ‎ ‎ ‎ ‎ ................(1)‎ ‎ 代入（1）式得 ........................(2)‎ ‎ 当时， 仍满足（2）式。‎ ‎ ‎ ‎（3）设直线的倾斜角为，由于由（2）可得 ‎ ，‎ ‎ ‎ ‎ 当时，取得最小值 ‎2009年普通高等学校招生全国统一考试（安徽卷）‎ 数学文科 一：选择题：本大题10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1、是虚数单位，等于 ‎ （A） （B） （C） （D）‎ 答案：选D 解析：‎ ‎（2）若集合A={x∣（2x+1）（x-3）＜0｝，则A∩B是 ‎ （A） {1,2,3,} (B) {1,2, } (C) {4,5} (D) {1,2,3,4,5}‎ 答案：选B 解析：，，∴‎ ‎（3）不等式组所表示的平面区域的面积等于 A B C x y O ‎（A）． （B）. （C）. （D）. ‎ 答案：选C 解析：不等式表示的平面区域如图所示阴影部分△ABC 由得A（1，1），又B（0，4），C（0，）‎ ‎∴S△ABC=。‎ ‎(4) “＞b+d ”是“＞b且c＞d ”的 ‎（A）必要不充分条件 （B）充分不必要条件 ‎（C）充分必要条件 （D）既不充分也不必要条件 ‎ 答案：选A 解析：由＞b且c＞d＞b+d，而由＞b+d 不能推出＞b且c＞d，可举反例。‎ ‎（5）已知为等差数列，++=105，=99，则等于 ‎（A）－1 （B） 1 （C） 3 （D 7 ‎ 答案：选B 解析：由++=105得即，由=99得即 ‎∴，。‎ ‎（6）下列曲线中离心率为的是 ‎（A）． （B）. （C）. （D）. ‎ 答案：选B 解析；由得，，观察各选项即得。‎ ‎（7）直线过点（－1，2）且与直线2x－3y＋4=0垂直，则的方程是 ‎ ‎（A）3x＋2y－1=0 （B）3x＋2y＋7=0 （C）2x－3y＋5=0 （D） 2x－3y＋8=0‎ 答案：选A 解析：，∴的方程为，即 ‎ （8）＜b,函数的图象可能是 答案：选C 解析：‎ ‎（9）．设函数，其中，则导数的取值范围是（A）． （B）. （C） （D ‎ 答案：选D 解析：，∴‎ ‎∴。‎ ‎（10）考察正方体6个面的中心，从中任意选3个点连成三角形，再把剩下的3个点也连成三角形，则所得的两个三角形全等的概率等于 ‎（A）．1 （B）. （C） （D）0‎ 答案：选A 解析：不妨设上下面的中心为A、B左右面的中心为C、D前后面的中心为E、F如图所示。‎ A B C D E F 从中任选3个点连成三角形可分两类：‎ 一是相对面的中心两点及被这两个面所夹四个面中心的 任意一面的中心，构成的是等腰直角三角形，此时剩下 的3个点也连成一个与其全等的三角形。‎ 二是所选3个点所在的平面中没有任何两个面是相对面 即此三个面彼此相邻，此时构成的是正三角形，‎ 同时剩下的3个点也构成正三角形。故所求概率是1。‎ 二．填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。‎ 开始 输出 结束 是 否 ‎（11）在空间直角坐标系中，已知点A（1，0，2），B(1，－3，1)，点M在y轴上，且M到A与到B的距离相等，则M的坐标是_______ ‎ 答案：‎ 解析：设 ，则由得 ‎，解得 即M的坐标是 ‎(12)程序框图（即算法流程图）如图所示，其输入结果是_______‎ 答案：127‎ 解析：由程序框图知，循环体被执行后的值依次为3、7、15、31、‎ ‎63、127，故输出的结果是127。‎ ‎(13)从长度分别为2、3、4、5的四条线段中任意取出三条，则以这三条线段为边可以构成三角形的概率是________ ‎ ‎ 答案：‎ 解析：从长度为2、3、4、5的四条线段中任意趣出3条共有4种不同的取法，其中可构成三角形的有（2，3，4），（2，4，5），（3，4，5）三种，故所求概率 A B C D E F ‎（14）在平行四边形ABCD中，E和F分别是边CD和BC的中点，若=+,其中,R ,则＋ _____ .‎ 答案：‎ 解析：如图 ‎，∴，∴‎ ‎（15）对于四面体ABCD，下列命题正确的是_________（写出所有正确命题的编号）。‎ 相对棱与所在的直线是异面直线；‎ 由顶点A作四面体的高，其垂足是BCD的三条高线的交点；‎ 若分别作ABC和ABD的边AB上的高，则这两条高的垂足重合；‎ 任何三个面的面积之和都大于第四个面的面积；‎ 分别作三组相对棱中点的连线，所得的三条线段相交于一点。‎ 解析：①④⑤‎ 解析：命题①显然正确，不然与共面，四面体不存在了.‎ 命题②不正确，BCD的三条高线的交点固定时，顶点还可以移动.‎ 命题③不正确，任选上两点作垂足，分别在垂线上取可组成四面体。‎ 命题④正确，3个面组成的曲面面积一定大于一个平面三角形的面积。 ‎ 命题⑤正确，设中点为，中点为,则,‎ 于是的中点为,同理其它两对棱连线中点也是点。 ‎ 三．解答题;本大题共6小题，共75分。解答应写出文字说明、证明过程或演算步骤。解答写在答题卡上的指定区域内。‎ ‎（16）（本小题满分12分）‎ 在ABC中，C－A=, sinB=。‎ ‎（I）求sinA的值；‎ ‎ (II)设AC=，求ABC的面积 解：本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识，考查运算求解能力。‎ ‎（Ⅰ）由，且，∴，∴，‎ A B C ‎∴，又，∴‎ ‎（Ⅱ）如图，由正弦定理得 ‎∴，又 ‎∴‎ ‎（17）（本小题满分12分）‎ 某良种培育基地正在培育一种小麦新品种A，将其与原有的一个优良品种B进行对照试验，两种小麦各种植了25亩，所得亩产数据（单位：千克）如下 品种A: 357,359,367,368,375,388,392,399,400,405,412,414,‎ ‎ 415,421,423,423,427,430,430,434,443,445,445,451,454‎ 品种B：363，371，374，383，385，386，391，392，394，394,395，397‎ ‎ 397，400，401，401，403，406，407，410，412，415，416，422，430‎ ‎（I）完成所附的茎叶图 ‎（II）用茎叶图处理现有的数据，有什么优点？‎ ‎（III）通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论。‎ A ‎7 35 ‎ ‎7 36 3 ‎ ‎5 37 1 4‎ ‎ 8 38 3 5 6 ‎ ‎ 9 2 39 1 2 4 4 5 7 7‎ ‎ 5 0 40 0 1 1 3 6 7‎ ‎ 5 4 2 41 0 2 5 6 ‎ ‎7 3 3 1 42 2‎ ‎ 4 0 0 43 0‎ ‎ 5 5 3 44‎ ‎ 4 1 45‎ B 解：本小题主要考查茎叶图统计的基本思想方 法，考查分析样本数据、从样本数据中提取基 本的数字特征、进行统计推断的能力和应用意识。‎ ‎(Ⅰ)茎叶图如图所示：‎ ‎(Ⅱ)由于每个品种的数据都只有25个，样本不大，‎ 画茎叶图很方便；此时茎叶图不仅清晰明了地展 示了数据的分布状况，便于比较，没有任何信息 损失，而且可以随时记录新的数据。‎ ‎（Ⅲ）通过观察茎叶图可以看出：‎ ‎①品种A的亩产平均数（或均值）比品种B高；‎ ‎②品种A的亩产标准差（或方差）比品种B大，‎ 故品种A的亩产稳定性较差。‎ ‎（18）（本小题满分12分）‎ 已知椭圆（a＞b＞0）的离心率为，以原点为圆心、椭圆短半轴长为半径的圆与直线相切，‎ ‎（1）求与；‎ ‎（2）设该椭圆的左，右焦点分别为和，直线过且与轴垂直，动直线与轴垂直，交与点.求线段垂直平分线与的交点的轨迹方程，并指明曲线类型。‎ 解：本小题主要考查椭圆、抛物线的方程，点到直线的距离公式，直线和曲线的位置关系等基础知识，考查综合运用知识分析问题、解决问题的能力.‎ ‎（1）由得，又，∴，∴。‎ ‎（2）(方法一)由得.‎ 设则.由,得 此轨迹是抛物线.‎ ‎(方法二)因为点在线段的垂直平分线上,所以,即到的距离等于到的距离.此轨迹是以为焦点、为准线的抛物线,轨迹方程为 ‎（19）（本小题满分12分）‎ 已知数列{} 的前项和，数列{}的前n项和 ‎（1）求数列{}与{}的通项公式；‎ ‎（2）设，证明：当且仅当n≥3时，＜‎ 解：本小题主要考查等差数列、等比数列，不等式等有关知识，考查数列的通项与其前项和之间的关系，考查抽象概括和运算求解能力。‎ 当时， ‎ 当时，‎ 也适合上式，所以数列{}的通项公式 当时，，∴‎ 当时，，∴‎ ‎∴数列是以1为首项，为公比的等比数列，所以数列{}的通项公式。‎ ‎（2）由（1）知，∴‎ 当时，2，当时，‎ 当 时，，‎ 因此，当且仅当n≥3时，＜‎ ‎（20）本小题满分13分 A B C D E F 第20题图 如图，ABCD是边长为2的正方形，直线与平面ABCD平行，E和F式上的两个不同点，且EA=ED，FB=FC, 和是平面ABCD内的两点，和都与平面ABCD垂直，‎ ‎（1）证明：直线垂直且平分线段AD：‎ ‎（2）若∠EAD=∠EAB,EF2,求多面体ABCDEF的体积。‎ 解：本小题主要考查直线与直线、直线与平面、平面与平面的位置关系以及空间几何体的体积计算等知识，考查空间想象能力和推理论证能力。‎ 由且面ABCD，∴点在线段AD的垂直平分线上，‎ 同理点在线段BC 的垂直平分线上，又ABCD是正方形 ‎∴线段BC 的垂直平分线就是线段AD的垂直平分线，‎ 即点、都在线段AD的垂直平分线，所以直线垂直且平分线段AD。‎ ‎（2）连接EB、EC。由题设知，多面体ABCDEF可分割成正四棱锥E－ABCD和正四面体E－BCF两部分。‎ 设AD的中点为M，在Rt△MEE/中，由于ME/=1，ME=，∴EE/=‎ ‎∴‎ 又 ‎∴多面体ABCDEF的体积为。‎ ‎（21）（本小题满分14分）‎ ‎ 已知函数，a＞0，‎ ‎（1）讨论的单调性;‎ ‎（2）设a=3，求在区间[1，]上值域。其中e=2.71828…是自然对数的底数。‎ 解：本小题主要考查函数的定义域、值域、最值，利用导数研究函数的单调性、极值等知识，考查分类讨论的思想和运算求解的能力 ‎（1）函数的定义域是，导函数 设二次方程的判别式 当，即时，恒成立，‎ ‎∴是上的单调递增函数。‎ 当，即时，方程有两个不同的实根 ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ 单调递增 极大 单调递减 极小 单调递增 此时在上单调递增，在上单调递减，在上单调递增。‎ ‎（2）当时，方程有两个不同的实根。‎ 由（1）知，在上是减函数，在上增函数。‎ 又 所以函数在区间上的值域为。‎ ‎ ‎ ‎ 绝密★启用前 ‎2010年普通高等学校招生全国统一考试(安徽卷)‎ ‎ 数 学(文科)‎ ‎ 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，第Ⅰ卷第1至第2页，第Ⅱ卷第3至第4页。全卷满分l50分，考试时间l20分钟。‎ 参考公式：‎ ‎ S表示底面积，h表示底面上的高 如果事件A与B互斥，那么 棱柱体积V=Sh ‎ P(A+B)=P(A)+P(B） 棱锥体积V=‎ 第Ⅰ卷(选择题 共50分)‎ 一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中．只有一项是符合题目要求的．‎ ‎(1)若A=，B=，则=‎ ‎ (A)(-1，+∞) (B)(-∞，3) (C)(-1，3) (D)(1，3)‎ 答案：C 解析：画数轴易知.‎ ‎(2)已知，则i()=‎ ‎ (A) (B) (C) (D)‎ 答案：B 解析：直接计算.‎ ‎(3)设向量,,则下列结论中正确的是 ‎(A) (B)‎ ‎(C) (D)与垂直 答案：D 解析：利用公式计算，采用排除法.‎ ‎（4）过点（1，0）且与直线x-2y-2=0平行的直线方程是 ‎（A）x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 （D）x+2y-1=0‎ 答案：A 解析：利用点斜式方程.‎ ‎(5)设数列｛｝的前n项和=，则的值为 ‎（A） 15 (B) 16 (C) 49 （D）64‎ 答案：A 解析：利用=S8-S7，即前8项和减去前7项和.‎ ‎（6）设abc＞0,二次函数f(x)=ax2+bx+c的图像可能是 答案：D 解析：利用开口方向a、对称轴的位置、y轴上的截距点c之间关系，结合abc＞0产生矛盾，采用排除法易知.‎ ‎（7）设a=，b=,c=，则a，b，c的大小关系是 ‎（A）a＞c＞b （B）a＞b＞c （C）c＞a＞b （D）b＞c＞a 答案：A 解析：利用构造幂函数比较a、c再利用构造指数函数比较b、c.‎ ‎（8）设x,y满足约束条件则目标函数z=x+y的最大值是 ‎（A）3 （B） 4 （C） 6 （D）8‎ 答案：C 解析：画出可行域易求.‎ ‎（9）一个几何体的三视图如图，该几何体的表面积是 ‎（A）372 （C）292 ‎ ‎（B）360 （D）280‎ 答案：B 解析：可理解为长8、宽10、高2的长方体和长6、宽2、高8的长方体组合而成,注意2×6重合两次，应减去.‎ ‎ ‎ ‎（10）甲从正方形四个顶点中任意选择两个顶点连成直线，乙也从该正方形四个顶点中任意选择两个顶点连成直线，则所得的两条直线相互垂直的概率是 ‎（A） （B） （C） （D）‎ 答案：C 解析：所有可能有6×6，所得的两条直线相互垂直有5×2.‎ 数 学(文科)(安徽卷)‎ 第Ⅱ卷(非选择题共100分)‎ 二．填空题：本大题共5小题，每小题5分，共25分．把答案填在答题卡的相应位置·‎ ‎(11)命题“存在x∈R，使得x2+2x+5=0”的否定是 ‎ 答案：对任何X∈R，都有X2+2X+5≠0 ‎ 解析：依据“存在”的否定为“任何、任意”，易知.‎ ‎(12)抛物线y2=8x的焦点坐标是 ‎ 答案：（2,0） 解析：利用定义易知.‎ ‎(13)如图所示，程序框图(算法流程图)的输出值x= ‎ 答案：12 解析：运算时X顺序取值为: 1,2,4,5,6,8,9,10,12.‎ ‎(14)某地有居民100000户，其中普通家庭99 000户,高收入家庭1 000户．从普通家庭中以简单随机抽样方式抽取990户，从高收入家庭中以简单随机抽样方式抽取l00户进行调查，发现共有120户家庭拥有3套或3套以上住房，其中普通家庭50户，高收人家庭70户．依据这些数据并结合所掌握的统计知识，你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 .‎ 答案：5.7% 解析： ，，易知.‎ ‎(15)若a>0,b>0,a+b=2，则下列不等式对一切满足条件的a，b恒成立的是 . (写出所有正确命题的编号)．‎ ‎①ab≤1； ②+≤； ③a2+b2≥2； ④a3+b3≥3; ‎ 答案：①,③,⑤ 解析：①,⑤化简后相同，令a=b=1排除②、易知④ ，再利用易知③正确 三、解答题：本大题共6小题．共75分．解答应写出文字说明、证明过程或演算步骤．解答写在答题卡上的指定区域内.‎ (16) ‎△ABC的面积是30，内角A,B,C,所对边长分别为a，b，c，cosA=.‎ (1) 求 (2) 若c-b=1，求a的值.‎ ‎（本小题满分12分）本题考查同角三角形函数基本关系，三角形面积公式，向量的数量积，利用余弦定理解三角形以及运算求解能力.‎ 解：由cosA=，得sinA= =.‎ 又bc sinA=30，∴bc=156. ‎ ‎（1）=bc cosA=156·=144.‎ ‎（2）a2=b2+c2-2bc cosA=(c-b)2+2bc(1-cosA)=1+2·156·(1-)=25，‎ ‎∴a=5‎ （17） 椭圆E经过点A（2,3），对称轴为坐标轴，焦点F1，F2在x轴上，离心率.‎ (1) 求椭圆E的方程；‎ (2) 求∠F1AF2的角平分线所在直线的方程.‎ ‎（本小题满分12分）本题考查椭圆的定义，椭圆的标准方程及简单几何性质，直线的点斜式方程与一般方程，点到直线的距离公式等基础知识，考查解析几何的基本思想和综合运算能力.‎ 解：（1）设椭圆E的方程为 由e=，得=，b2=a2-c2 =3c2. ∴ 将A（2,3）代入，有 ，解得：c=2, 椭圆E的方程为 ‎（Ⅱ）由(Ⅰ)知F1（-2,0），F2（2,0），所以直线AF1的方程为 y=(X+2)，‎ 即3x-4y+6=0. 直线AF2的方程为x=2. 由椭圆E的图形知，‎ ‎∠F1AF2的角平分线所在直线的斜率为正数.‎ 设P（x，y）为∠F1AF2的角平分线所在直线上任一点，‎ 则有 若3x-4y+6=5x-10，得x+2y-8=0，其斜率为负，不合题意，舍去.‎ 于是3x-4y+6=-5x+10，即2x-y-1=0.‎ 所以∠F1AF2的角平分线所在直线的方程为2x-y-1=0.‎ ‎18、（本小题满分13分）‎ ‎ 某市2010年4月1日—4月30日对空气污染指数的检测数据如下（主要污染物为可吸入颗粒物）:‎ ‎ 61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,‎ ‎ 77,86,81,83,82,82,64,79,86,85,75,71,49,45,‎ ‎(Ⅰ) 完成频率分布表；‎ ‎（Ⅱ）作出频率分布直方图；‎ ‎（Ⅲ）根据国家标准，污染指数在0~50之间时，空气质量为优：在51~100之间时，为良；在101~150之间时，为轻微污染；在151~200之间时，为轻度污染。‎ 请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价.‎ ‎（本小题满分13分）本题考查频数，频数及频率分布直方图，考查运用统计知识解决简单实际问题的能力，数据处理能力和应用意识.‎ 解：(Ⅰ) 频率分布表：‎ 分 组 频 数 频 率 ‎［41,51)‎ ‎2‎ ‎［51,61)‎ ‎1‎ ‎［61,71)‎ ‎4‎ ‎［71,81)‎ ‎6‎ ‎［81,91)‎ ‎10‎ ‎［91,101)‎ ‎5‎ ‎［101,111)‎ ‎2‎ 空气污染指数 ‎4151 61 71 81 91 101 111‎ 频率 组距 ‎ （Ⅱ）频率分布直方图：‎ ‎（Ⅲ）答对下述两条中的一条即可：‎ ‎（i）该市一个月中空气污染指数有2天处于优的水平，占当月天数的. 有26天处于良好的水平，占当月天数的. 处于优或良的天数共有28天，占当月天数的. 说明该市空气质量基本良好.‎ ‎（ii）轻微污染有2天，占当月天数的. 污染指数在80以上的接近轻微污染的天数有15天，加上处于轻微污染的天数，共有17天，占当月天数的，超过50%. 说明该市空气质量有待进一步改善.‎ (19) ‎(本小题满分13分)‎ 如图，在多面体ABCDEF中，四边形ABCD是正方形，AB=2EF=2，EF∥AB,EF⊥FB,∠BFC=90°，BF=FC,H为BC的中点，‎ ‎(Ⅰ)求证：FH∥平面EDB;‎ ‎（Ⅱ）求证：AC⊥平面EDB; ‎ ‎（Ⅲ）求四面体B—DEF的体积；‎ ‎（本小题满分13分）本题考查空间线面平行，线面垂直，面面垂直，体积的计算等基础知识，同时考查空间想象能力与推理论证能力.‎ ‎(Ⅰ) 证：设AC与BD交于点G，则G为AC的中点. 连EG，GH，由于H为BC的中点，故GH∥AB且 GH=AB 又EF∥AB且 EF=AB ‎∴EF∥GH. 且 EF=GH ∴四边形EFHG为平行四边形.‎ ‎∴EG∥FH，而EG 平面EDB，∴FH∥平面EDB.‎ ‎（Ⅱ）证：由四边形ABCD为正方形，有AB⊥BC.‎ 又EF∥AB，∴ EF⊥BC. 而EF⊥FB，∴ EF⊥平面BFC，∴ EF⊥FH.‎ ‎∴ AB⊥FH.又BF=FC H为BC的中点，FH⊥BC.∴ FH⊥平面ABCD.‎ ‎∴ FH⊥AC. 又FH∥EG，∴ AC⊥EG. 又AC⊥BD，EG∩BD=G，‎ ‎∴ AC⊥平面EDB.‎ ‎（Ⅲ）解：∵ EF⊥FB，∠BFC=90°，∴ BF⊥平面CDEF.‎ ‎∴ BF为四面体B-DEF的高. 又BC=AB=2, ∴ BF=FC= ‎ ‎（20）（本小题满分12分）‎ ‎ 设函数f（x）=sinx-cosx+x+1, 0﹤x﹤2 ,求函数f(x)的单调区间与极值.‎ ‎（本小题满分12分）本题考查导数的运算，利用导数研究函数的单调性与极值的方法，考查综合运用数学知识解决问题的能力.‎ 解：由f(x)=sinx-cosx+x+1，0﹤x﹤2,‎ 知=cosx+sinx+1，‎ 于是=1+sin(x+ ).‎ 令=0，从而sin(x+ )=-，得x= ，或x=.‎ 当x变化时，，f(x)变化情况如下表：‎ X ‎(0, )‎ ‎（，）‎ ‎（，2 ）‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ f(x)‎ 单调递增↗‎ ‎+2‎ 单调递减↘‎ 单调递增↗‎ 因此，由上表知f(x)的单调递增区间是（0, ）与（，2 ），单调递减区间是（，），极小值为f（）=，极大值为f（）= +2.‎ ‎（21）（本小题满分13分)‎ 设，...,,…是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线y=x相切，对每一个正整数n,圆都与圆相互外切，以表示的半径，已知为递增数列.‎ ‎(Ⅰ)证明：为等比数列；‎ ‎（Ⅱ）设=1，求数列的前n项和. ‎ ‎（本小题满分13分）本题考查等比数列的基本知识，利用错位相减法求和等基本方法，考查抽象能力以及推理论证能力.‎ 解：(Ⅰ)将直线y=x的倾斜角记为 ， 则有tan = ，sin =.‎ 设Cn的圆心为（，0），则由题意知= sin = ，得 = 2 ；同理 ‎，题意知将 = 2代入，解得 rn+1=3rn.‎ 故{ rn }为公比q=3的等比数列.‎ ‎（Ⅱ）由于r1=1，q=3，故rn=3n-1，从而 =n·，‎ 记Sn=， 则有 Sn=1+2·3-1+3·3-2+………+n·. ①‎ ‎=1·3-1+2·3-2+………+(n-1) ·+n·. ② ①-②，得 ‎=1+3-1 +3-2+………+-n· =- n·= –(n+)· ‎ Sn= – (n+)·.‎ ‎ ‎ ‎ 2011年普通高等学校招生全国统一考试（安徽卷）‎ 数学（文科）‎ 参考公式：‎ 椎体体积，其中S为椎体的底面积，h为椎体的高。‎ 若（x，y），（x，y）…，（x，y）为样本点，为回归直线，则 ，‎ ‎，‎ 说明：若对数据适当的预处理，可避免对大数字进行运算。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎