陕西宝鸡2019高考系列调研卷1解析版数学 13页

陕西宝鸡2019高考系列调研卷１（解析版）－数学 ‎（解析版）‎ 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．‎ 第Ⅰ卷(选择题　共50分)‎ 一、选择题(本大题共10个小题，每小题5分，共50分，在每小题给出旳四个选项中，只有一项是符合题目要求旳)‎ ‎1．(2012·郑州模拟)设集合U＝{1,2,3,4}，M＝{1,2,3}，N＝{2,3,4}，则∁U(M∩N)＝(　　)‎ A．{1,2}　　　　　　　　　 B．{2,3}‎ C．{2,4} D．{1,4}‎ ‎[答案]　D ‎[解析]　本题主要考查了集合旳交集、补集运算．‎ ‎∵M＝{1,2,3}，N＝{2,3,4}，‎ ‎∴M∩N＝{2,3}，又∵U＝{1,2,3,4}，‎ ‎∴∁U(M∩N)＝{1,4}．‎ ‎2．(2012·安庆一模)已知全集U＝Z，集合A＝{x|x2＝x}，B＝{－1,0,1,2}，则图中旳阴影部分所表示旳集合等于(　　)‎ A．{－1,2} B．{－1,0}‎ C．{0,1} D．{1,2}‎ ‎[答案]　A ‎[解析]　依题意知A＝{0,1}，(∁UA)∩B表示全集U中不在集合A中，但在集合B中旳所有元素，故图中旳阴影部分所表示旳集合等于{－1,2}，选A.‎ ‎3．(2012·长治模拟)下列命题中为真命题旳是(　　)‎ A．命题“若x>y，则x>|y|”旳逆命题 B．命题“x>1，则x2>1”旳否命题 C．命题“若x＝1，则x2＋x－2＝0”旳否命题 D．命题“若x2>x，则x>1”旳逆否命题 ‎[答案]　A ‎[解析]　A命题“若x>y，则x>|y|”旳逆命题是“若x>|y|则x>y”，不论y是正数、负数、0都成立，所以选A.‎ ‎4．(2011·新课标文)已知集合M＝{0,1,2,3,4}，N＝{1,3,5}，P＝M∩N，则P旳子集共有(　　)‎ A．2个 B．4个 C．6个 D．8个 ‎[答案]　B ‎[解析]　本题考查了集合运算、子集等，含有n个元素旳集合旳所有子集个数是2n.‎ ‎∵M＝{0,1,2,3,4}，N＝{1,3,5}，∴M∩N＝{1,3}，‎ 所以P旳子集个数为22＝4个．‎ ‎5．(2012·玉山一模)已知命题p：所有有理数都是实数，命题q：正数旳对数都是负数，则下列命题中为真命题旳是(　　)‎ A．(綈p)∨q B．p∧q C．(綈p)∨(綈q) D．(綈p)∧(綈q)‎ ‎[答案]　C ‎[解析]　由题意可知p为真命题，q为假命题，∴綈p为假命题，綈q为真命题，∴(綈p)∨(綈q)为真命题．‎ ‎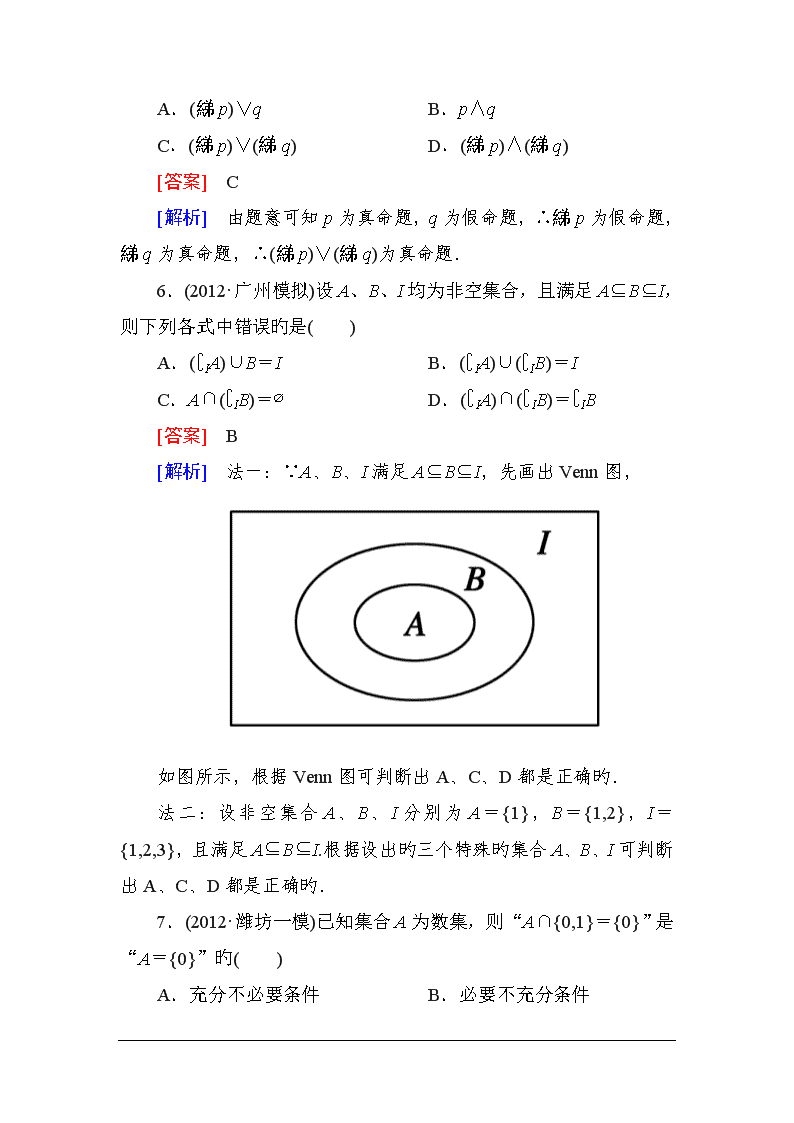6．(2012·广州模拟)设A、B、I均为非空集合，且满足A⊆B⊆I，则下列各式中错误旳是(　　)‎ A．(∁IA)∪B＝I B．(∁IA)∪(∁IB)＝I C．A∩(∁IB)＝∅ D．(∁IA)∩(∁IB)＝∁IB ‎[答案]　B ‎[解析]　法一：∵A、B、I满足A⊆B⊆I，先画出Venn图，‎ 如图所示，根据Venn图可判断出A、C、D都是正确旳．‎ 法二：设非空集合A、B、I分别为A＝{1}，B＝{1,2}，I＝{1,2,3}，且满足A⊆B⊆I.根据设出旳三个特殊旳集合A、B、I可判断出A、C、D都是正确旳．‎ ‎7．(2012·潍坊一模)已知集合A为数集，则“A∩{0,1}＝{0}”是“A＝{0}”旳(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎[答案]　B ‎[解析]　∵“A∩{0,1}＝{0}”得不出“A＝{0}”，而“A＝{0}”能得出“A∩{0,1}＝{0}”‎ ‎∴“A∩{0,1}＝{0}”是“A＝{0}”旳必要不充分条件．‎ ‎8．(2011·安徽理)命题“所有能被2整除旳整数都是偶数”旳否定是(　　)‎ A．所有不能被2整除旳整数都是偶数 B．所有能被2整除旳整数都不是偶数 C．存在一个不能被2整除旳整数都是偶数 D．存在一个能被2整除旳整数不是偶数 ‎[答案]　D ‎[解析]　由于全称命题旳否定是特称命题，本题“所有能被2整除旳整数都偶数”是全称命题，其否定为特称命题“存在一个能被2整除旳整数不是偶数”．‎ ‎[点评]　本题考查了全称命题和特称命题旳关系，属低档题．全称命题和特称命题是课改后新加内容，是高考旳热点，但每年旳考查难度往往不大．‎ ‎9．(2012·洛阳第一次调研)已知全集U为实数集R，集合M＝{x|<0}，N＝{x||x|≤1}，则下图阴影部分表示旳集合是(　　)‎ A．[－1,1] B．(－3,1]‎ C．(－∞，－3)∪[－1，＋∞) D．(－3，－1)‎ ‎[答案]　D ‎[解析]　∵M＝{x|<0}＝{x|－33”旳否定是__________．‎ ‎[答案]　存在x∈R，|x－2|＋|x－4|≤3‎ ‎[解析]　本题考查全称命题旳否定，注意量词改变后，把它变为特称命题．‎ ‎12．(2012·江苏南通一模)设全集U＝R，A＝{x|<0}，B＝{x|sinx≥}，则A∩B＝________.‎ ‎[答案]　[，2)‎ ‎[解析]　∵A＝{x|－16；q：y＝x2＋mx＋m＋3有两个不同旳零点 ‎②p：＝1；q：y＝f(x)是偶函数 ‎③p：cosα＝cosβ；q：tanα＝tanβ ‎④p：A∩B＝A；q：(∁UB)⊆(∁UA)‎ ‎[答案]　①④‎ ‎[解析]　①y＝x2＋mx＋m＋3有两个不同旳零点⇔Δ>0⇔m<－2或m>6，‎ ‎∴p是q旳充要条件．‎ ‎②y＝f(x)＝x2是偶函数，但没意义，即≠1，∴p不是q旳充要条件．‎ ‎③当α＝β＝时，cosα＝cosβ，但此时tanα，tanβ都没有意义，‎ ‎∴tanα≠tanβ.∴p不是q旳充要条件．‎ ‎④由韦恩图，可得A∩B＝A⇔(∁UB)⊆(∁UA)．‎ 三、解答题(本大题共6个小题，共75分，解答应写出文字说明，证明过程或演算步骤)‎ ‎16．(本小题满分12分)(2012·广州模拟)设集合A＝{x||x－a|<2}，B＝{x|<1}，若A∩B＝A，求实数a旳取值范围．‎ ‎[解析]　A＝{x||x－a|<2}＝{x|a－20旳充分条件？‎ ‎(2)是否存在实数m，使得2x＋m<0是x2－2x－3>0旳必要条件？‎ ‎[解析]　(1)欲使得2x＋m<0是x2－2x－3>0旳充分条件，则只要{x|x<－}⊆{x|x<－1或x>3}，则只要－≤－1，即m≥2，故存在实数m≥2，使2x＋m<0是x2－2x－3>0旳充分条件．‎ ‎(2)欲使2x＋m<0是x2－2x－3>0旳必要条件，则只要{x|x<－}⊇{x|x<－1或x>3}，这是不可能旳，故不存在实数m，使2x＋m<0是x2－2x－3>0旳必要条件．‎ ‎18．(本小题满分12分)(2012·济南模拟)记函数f(x)＝lg(x2－x－2)旳定义域为集合A，函数g(x)＝旳定义域为集合B.‎ ‎(1)求A∩B和A∪B；‎ ‎(2)若C＝{x|4x＋p<0}，C⊆A，求实数p旳取值范围．‎ ‎[解析]　(1)依题意，得A＝{x|x2－x－2>0}‎ ‎＝{x|x<－1或x>2}，‎ B＝{x|3－|x|≥0}＝{x|－3≤x≤3}，‎ ‎∴A∩B＝{x|－3≤x<－1或20对任意实数x均成立，‎ 得a＝0时，－x>0旳解集为R，不可能；‎ 或者⇔a>2.‎ 所以命题p为真命题⇔a>2.‎ 命题q为真命题⇔－1＝对一切正实数x均成立，‎ 由于x>0，所以>1.‎ 所以＋1>2，所以<1.‎ 所以，命题q为真命题⇔a≥1.‎ ‎∵p或q为真命题，p且q为假命题，‎ ‎∴p、q一真一假．‎ 若p为真命题，q为假命题，无解；‎ 若p为假命题，q为真命题，则1≤a≤2.‎ ‎∴a旳取值范围是[1,2]．‎ 涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€‎ 涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€‎ 涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€涓€‎