高三文科数学高考模拟试卷含答案 9页

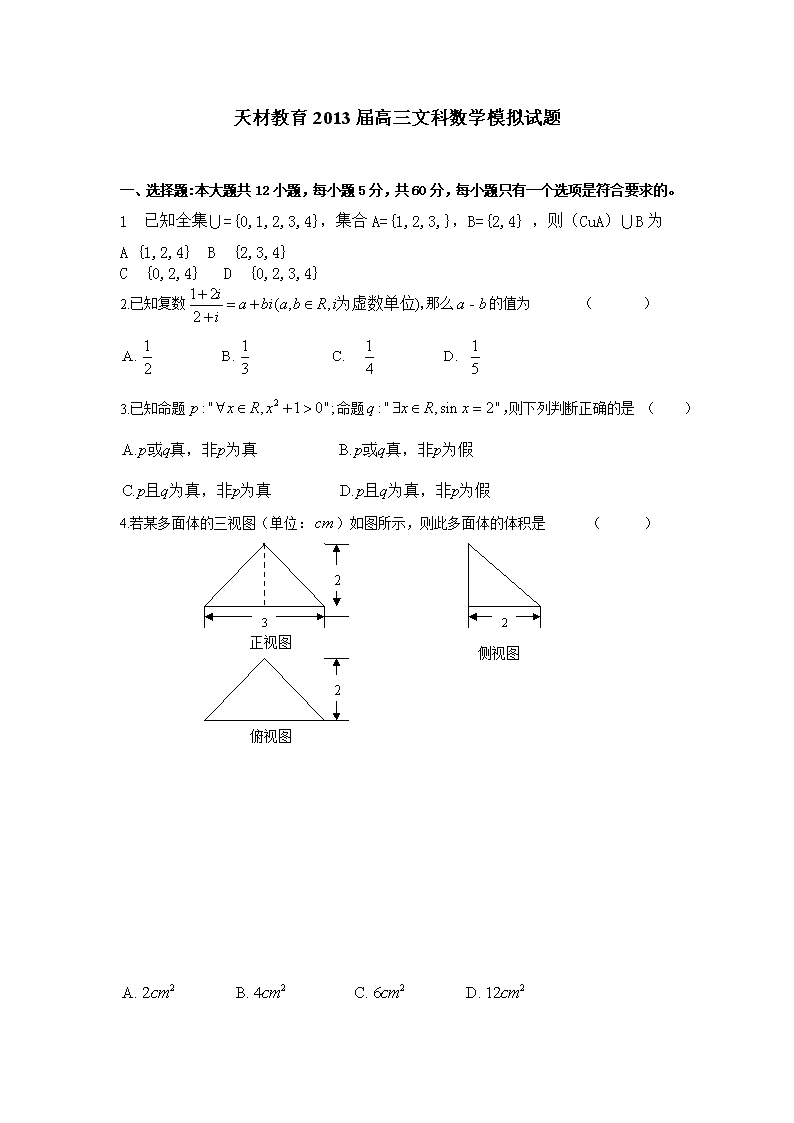
天材教育2013届高三文科数学模拟试题 一、选择题:本大题共12小题，每小题5分，共60分，每小题只有一个选项是符合要求的。‎ ‎1 已知全集={0,1,2,3,4}，集合A={1,2,3,}，B={2,4} ，则（CuA）B为 A {1,2,4} B {2,3,4}‎ C {0,2,4} D {0,2,3,4}‎ 2. 已知复数那么的值为 （ ）‎ ‎ ‎ 3. 已知命题命题，则下列判断正确的是 （ ）‎ ‎ ‎ ‎ ‎ 4. 若某多面体的三视图（单位：）如图所示，则此多面体的体积是 （ ）‎ ‎2‎ ‎3‎ 正视图 ‎2‎ 侧视图 俯视图 ‎2‎ ‎ ‎ 2. 某产品的成本费用与销售额的统计数据如下表， ‎ 成本费用x(万元)‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 销售额y（万元）‎ ‎26‎ ‎39‎ ‎39‎ ‎54‎ ‎ 根据上表可得回顾方程中的为9.4，据此模型预报成本费用为6万元时销售额为 （ ） ‎ ‎72.0万元 67.7万元 65.5万元 63.6万元 3. 设双曲线的离心率为，且过点（4,0），则此双曲线的方程为（ ）‎ ‎ ‎ 7. 已知，则的大小关系为（ ）‎ ‎ ‎ 8. 在中分别为角的对边，若，且的面积为，则角（ ）‎ ‎ ‎ ‎9 过点A（1，－1）、B（－1，1）且圆心在直线x＋y－2＝0上的圆的方程是 （ ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎10 函数的图形的一条对称轴的方程是 （ ）‎ ‎ （A） （B） （C） （D）‎ ‎11 若、都是R上的单调函数，有如下命题：‎ ‎ ①若、都单调递增，则单调递增 ‎ ②若、都单调递减，则单调递减 ‎ ③若、都单调递增，则单调递增 ‎ ④若单调递增，单调递减，则单调递增 ‎ ⑤若单调递减，单调递增，单调递减 ‎ 其中正确的是 （ ）‎ ‎ （A）①② （B）②③④ （C）③④⑤ （D）④⑤‎ ‎12 已知函数，若函数有3个零点，则实数的取值范围是（ a ）‎ ‎(0,1) (0,2) (1,2) (2,3)‎ 二、填空题:本大题共4小题，每小题5分共20分。.‎ 是 否 A=1，S=0‎ A<9‎ A=A+2‎ 结束 开 始 输出S S=S+A ‎（14题）‎ ‎14.在一次运动员选拔中，测得5名选手身高（单位：）分布的茎叶图如图，则5名运动员身高的标准差为 .‎ ‎ 18 0 2 4‎ ‎ 17 6 8‎ ‎（13题）‎ ‎15.如图所示的程序框图，该程序运行后输出的结果为 .‎ ‎16 已知m、n是直线，是平面，给出下列命题 ‎（1）若，，则 ‎（2）若则 ‎（3）若内不共线三点 A，B，C到的距离都相等，则 ‎（4）若且 ‎（5）若m,n为异面直线，且 则其中正确的是 .‎ 三、 解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤。‎ 17. ‎（本小题满分12分）‎ 某小学共有小学生2000名，各年级男、女学生人数如下表，已知在全校学生中素以及抽取1名，抽到三年级男生的概率为，现用分层抽样的方法在全校抽取200名学生。‎ （1） 应在三年级女生中抽取的学生人数为？‎ （2） 若在六个年级中随机抽取两个年级的女生，则两个年级女生数相差不超过20的概率为？‎ 一年级 二年级 三年级 四年级 五年级 六年级 女 生 ‎160‎ ‎180‎ ‎140‎ ‎230‎ ‎170‎ 男 生 ‎150‎ ‎150‎ ‎120‎ ‎180‎ ‎100‎ 18. ‎（本小题满分12分）‎ 已知函数。‎ ‎（Ⅰ）求函数的最小正周期和值域；‎ ‎（Ⅱ）若，求的值。‎ ‎19． （本题满分12分）‎ 已知四棱锥P－ABCD的直观图与三视图如图所示 ‎（1）求四棱锥P－ABCD的体积；‎ ‎（2）若E为侧棱PC的中点，求证：PA//平面BDE.‎ ‎20．已知是公差不为零的等差数列，a1＝1，且a1，a3，a9成等比数列.‎ ‎（Ⅰ）求数列{an}的通项; （Ⅱ）求数列{2an}的前n项和Sn.‎ ‎21．（12分）‎ 已知椭圆的焦点A（－4，0），B（4，0），过点B并垂直于x轴的直线与椭圆的一个交点为C，且|AC|+|BC|=10，椭圆上不同的两点满足条件：|BM|，|BC|，|BN|成等差数列.‎ ‎（1）求该椭圆方程;‎ ‎（2）求弦MN中点的横坐标.‎ ‎22．设函数 ‎ （1）求函数的单调区间；‎ ‎ （2）求在[—1，2]上的最小值；‎ 天材教育2013年届高三文科数学模拟试题 ‎（参考答案）‎ 一 选择题：CDBAC CCBCA DA 二．填空题：‎ ‎ 13、 14、‎ ‎15、 16 16．（2）（5）‎ 三．解答题：（本大题共6小题，共75分。解答应写出必要的过程或演算步骤。）‎ ‎17、（1）解：由题知，，………….. ………….. ……2分 抽样的比例为，所以应在三年级女生中抽取学生数为：（人）………….. ………….. ……4分 ‎（2）在六个年级中随机抽取两个年级的女生共有15种不同的取法：（160，180），（160,220），（160,140），（160,230），（160,170），（180，220），（180,140），（180,230），（180,170），（220,140），（220,230），（220,170），（140,230），（140,170），（230,170）。….. ………….. ……8分 设表示随机事件“所抽取的两个年级女生数相差不超过20”，则的基本事件有5种：（160,180），（160,140），（160,170），（180,170），（220.230）。.. ………….. ……10分 故所求概率为………….. ………….. ……12分 ‎18【解析】‎ ‎19.（1）解：由该四棱锥的三视图可知，该四棱锥P－ABCD的底面是边长为1的正方形，侧棱PC⊥底面ABCD，且PC=2. ∴。‎ ‎(2)连接BE,DE，AC，设，连接OE，在△PCA中，∵点E、点O为PC、AC的中点，∴∵OE平面BDE, PA平面BDE, ∴PA//平面BDE. ‎ ‎20解由题设知公差 由成等比数列得 解得(舍去)‎ 故的通项 ‎,‎ 由等比数列前n项和公式得 ‎21．解：（1）‎ ‎（2）设 又 ‎.‎ ‎22解：（1）…………2分 令 ‎—2‎ ‎（-2，0）‎ ‎0‎ ‎（0，1）‎ ‎1‎ ‎—‎ ‎0‎ ‎+‎ ‎0‎ ‎—‎ ‎0‎ ‎+‎ 减 极小 增 极大 减 极小 增 函数的增区间为 ‎…………5分 ‎ （2）当 所以 ………………8分