高考数学理专题目六第一讲统计及统计案例二轮复习 5页

第一讲　统计及统计案例 ‎1．(2013·高考湖南卷)某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件、80件、60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n＝(　　)‎ A．9　　　　　　　　　　　　　 B．10‎ C．12 D．13‎ ‎2．(2013·深圳市调研)某容量为180的样本的频率分布直方图共有n(n>1)个小矩形，若第一个小矩形的面积等于其余n－1个小矩形的面积之和的，则第一个小矩形对应的频数是(　　)‎ A．20 B．25‎ C．30 D．35‎ ‎3．(2013·高考辽宁卷)某班的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20，40)，[40，60)，[60，80)，[80，100]．若低于60分的人数是15，则该班的学生人数是(　　)‎ A．45 B．50‎ C．55 D．60‎ ‎4．某人身高176 cm，他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关，该人用线性回归分析的方法预测他孙子的身高约为(　　)‎ A．182 cm B．183 cm C．184 cm D．185 cm ‎5．为了普及环保知识，增强环保意识，某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试．统计得到成绩与专业的列联表：‎ 优秀 非优秀 总计 A班 ‎14‎ ‎6‎ ‎20‎ B班 ‎7‎ ‎13‎ ‎20‎ 总计 ‎21‎ ‎19‎ ‎40‎ 附：参考公式及数据 ‎(1)K2＝(其中n＝a＋b＋c＋d)；‎ ‎(2)独立性检验的临界值表：‎ P(K2≥k0)‎ ‎0.050‎ ‎0.010‎ k0‎ ‎3.841‎ ‎6.635‎ 则下列说法正确的是(　　)‎ A．有99%的把握认为环保知识测试成绩与专业有关 B．有99%的把握认为环保知识测试成绩与专业无关 C．有95%的把握认为环保知识测试成绩与专业有关 D．有95%的把握认为环保知识测试成绩与专业无关 ‎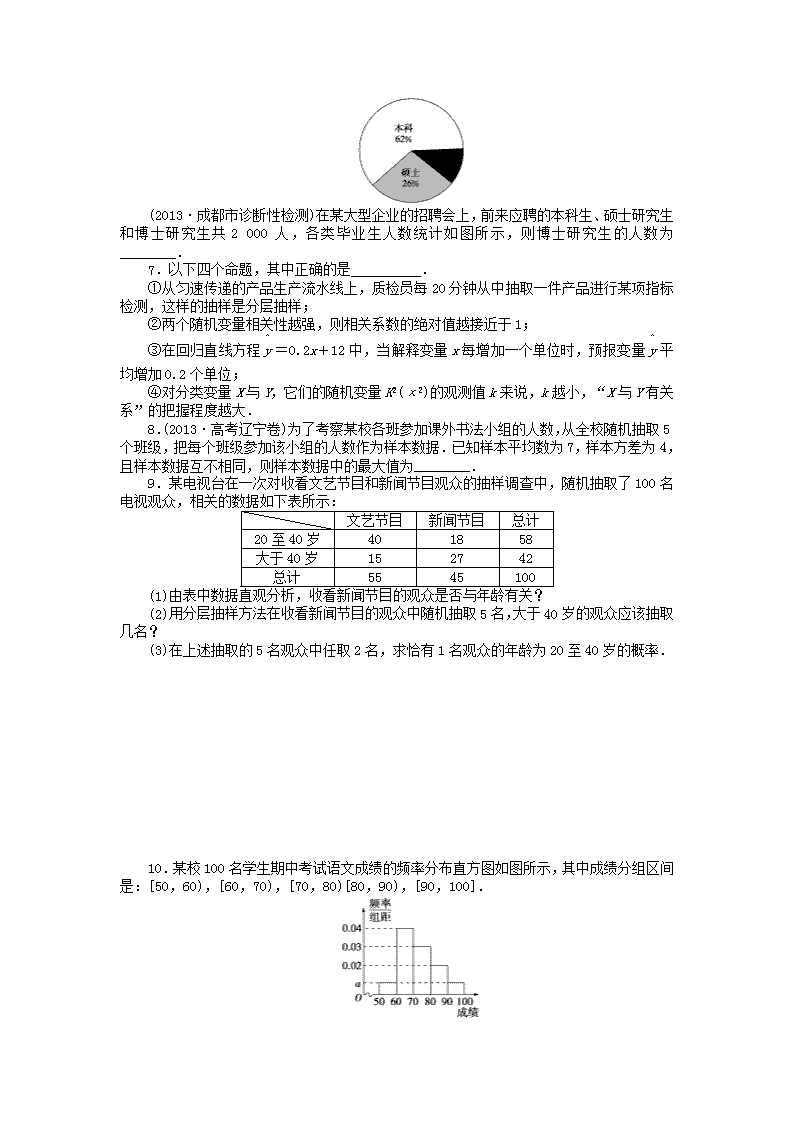6.‎ ‎(2013·成都市诊断性检测)在某大型企业的招聘会上，前来应聘的本科生、硕士研究生和博士研究生共2 000人，各类毕业生人数统计如图所示，则博士研究生的人数为________．‎ ‎7．以下四个命题，其中正确的是__________．‎ ‎①从匀速传递的产品生产流水线上，质检员每20分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；‎ ‎②两个随机变量相关性越强，则相关系数的绝对值越接近于1；‎ ‎③在回归直线方程＝0.2x＋12中，当解释变量x每增加一个单位时，预报变量平均增加0.2个单位；‎ ‎④对分类变量X与Y，它们的随机变量K2(χ2)的观测值k来说，k越小，“X与Y有关系”的把握程度越大．‎ ‎8．(2013·高考辽宁卷)为了考察某校各班参加课外书法小组的人数，从全校随机抽取5个班级，把每个班级参加该小组的人数作为样本数据．已知样本平均数为7，样本方差为4，且样本数据互不相同，则样本数据中的最大值为________．‎ ‎9．某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：‎ 文艺节目 新闻节目 总计 ‎20至40岁 ‎40‎ ‎18‎ ‎58‎ 大于40岁 ‎15‎ ‎27‎ ‎42‎ 总计 ‎55‎ ‎45‎ ‎100‎ ‎(1)由表中数据直观分析，收看新闻节目的观众是否与年龄有关？‎ ‎(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名，大于40岁的观众应该抽取几名？‎ ‎(3)在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为20至40岁的概率．‎ ‎10．某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60)，[60，70)，[70，80)[80，90)，[90，100]．‎ ‎(1)求图中a的值；‎ ‎(2)根据频率分布直方图，估计这100名学生语文成绩的平均数；‎ ‎(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50，90)之外的人数．‎ 分数段 ‎[50，60)‎ ‎[60，70)‎ ‎[70，80)‎ ‎[80，90)‎ x∶y ‎1∶1‎ ‎2∶1‎ ‎3∶4‎ ‎4∶5‎ ‎11．某体育训练队共有队员40人，下表为跳远成绩的分布表，成绩分为1～5个档次，例如表中所示跳高成绩为4分、跳远成绩为2分的队员为5人，将全部队员的姓名卡混合在一起，任取一张，该卡队员的跳高成绩为x，跳远成绩为y，(注：没有相同姓名的队员)‎ ‎　　　　y x　　　　‎ 跳　远 ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ 跳高 ‎5‎ ‎1‎ ‎3‎ ‎1‎ ‎0‎ ‎1‎ ‎4‎ ‎1‎ ‎0‎ ‎2‎ ‎5‎ ‎1‎ ‎3‎ ‎2‎ ‎1‎ ‎0‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎1‎ ‎6‎ ‎0‎ ‎2‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎3‎ ‎(1)求x＝4的概率及x＝4且y≥3的概率；‎ ‎(2)若跳远、跳高成绩为4分及其以上时为“优秀”，否则为“一般”，试问：一个人的跳高成绩是否“优秀”与跳远是否“优秀”有没有关系？‎ ‎(3)若跳远、跳高成绩相等时的人数为分别为m，n，试问：m，n是否具有线性相关关系？若有，求出回归直线方程．若没有请说明理由．‎ 答案：‎ ‎1．【解析】选D.依题意得＝，故n＝13.‎ ‎2．【解析】选C.设第一个小矩形的面积为x，则x＋5x＝1，得x＝，即第一个小矩形对应的频率为，∴第一个小矩形对应的频数为180×＝30.‎ ‎3．【解析】选B.根据频率分布直方图的特点可知，低于60分的频率是(0.005＋0.01)×20＝0.3，所以该班的学生人数是＝50.‎ ‎4．【解析】选D.由父亲与儿子身高的对应的数据如下表：‎ 父亲的身高(x)‎ ‎173‎ ‎170‎ ‎176‎ 儿子的身高(y)‎ ‎170‎ ‎176‎ ‎182‎ 所以回归直线方程为y＝x＋3，从而可预测他孙子的身高为182＋3＝185.‎ ‎5．【解析】选C.K2＝≈4.912，‎ 因为3.841