高考数学导数题型归纳 12页

导数题型归纳 请同学们高度重视：‎ 首先，关于二次函数的不等式恒成立的主要解法：‎ ‎1、分离变量；2变更主元；3根分布；4判别式法 ‎5、二次函数区间最值求法：（1）对称轴（重视单调区间）‎ 与定义域的关系 （2）端点处和顶点是最值所在 ‎ 其次，分析每种题型的本质，你会发现大部分都在解决“不等式恒成立问题”以及“充分应用数形结合思想”，创建不等关系求出取值范围。‎ ‎ 最后，同学们在看例题时，请注意寻找关键的等价变形和回归的基础 一、基础题型：函数的单调区间、极值、最值；不等式恒成立；‎ ‎1、此类问题提倡按以下三个步骤进行解决：‎ 第一步：令得到两个根；‎ 第二步：画两图或列表；‎ 第三步：由图表可知；‎ 其中不等式恒成立问题的实质是函数的最值问题，‎ ‎2、常见处理方法有三种：‎ 第一种：分离变量求最值-----用分离变量时要特别注意是否需分类讨论（>0,=0,<0）‎ 第二种：变更主元（即关于某字母的一次函数）-----（已知谁的范围就把谁作为主元）；‎ 例1：设函数在区间D上的导数为，在区间D上的导数为，若在区间D上，恒成立，则称函数在区间D上为“凸函数”，已知实数m是常数，‎ ‎（1）若在区间上为“凸函数”，求m的取值范围；‎ ‎（2）若对满足的任何一个实数，函数在区间上都为“凸函数”，求的最大值.‎ 解:由函数 得 ‎ ‎（1） 在区间上为“凸函数”，‎ 则 在区间[0,3]上恒成立 ‎ 解法一：从二次函数的区间最值入手：等价于 ‎ ‎ 解法二：分离变量法：‎ ‎∵ 当时, 恒成立,‎ ‎ 当时, 恒成立 等价于的最大值（）恒成立，‎ 而（）是增函数，则 ‎(2)∵当时在区间上都为“凸函数” ‎ 则等价于当时 恒成立 ‎ 解法三：变更主元法 ‎ 再等价于在恒成立（视为关于m的一次函数最值问题）‎ ‎-2‎ ‎2‎ ‎ ‎ ‎ ‎ 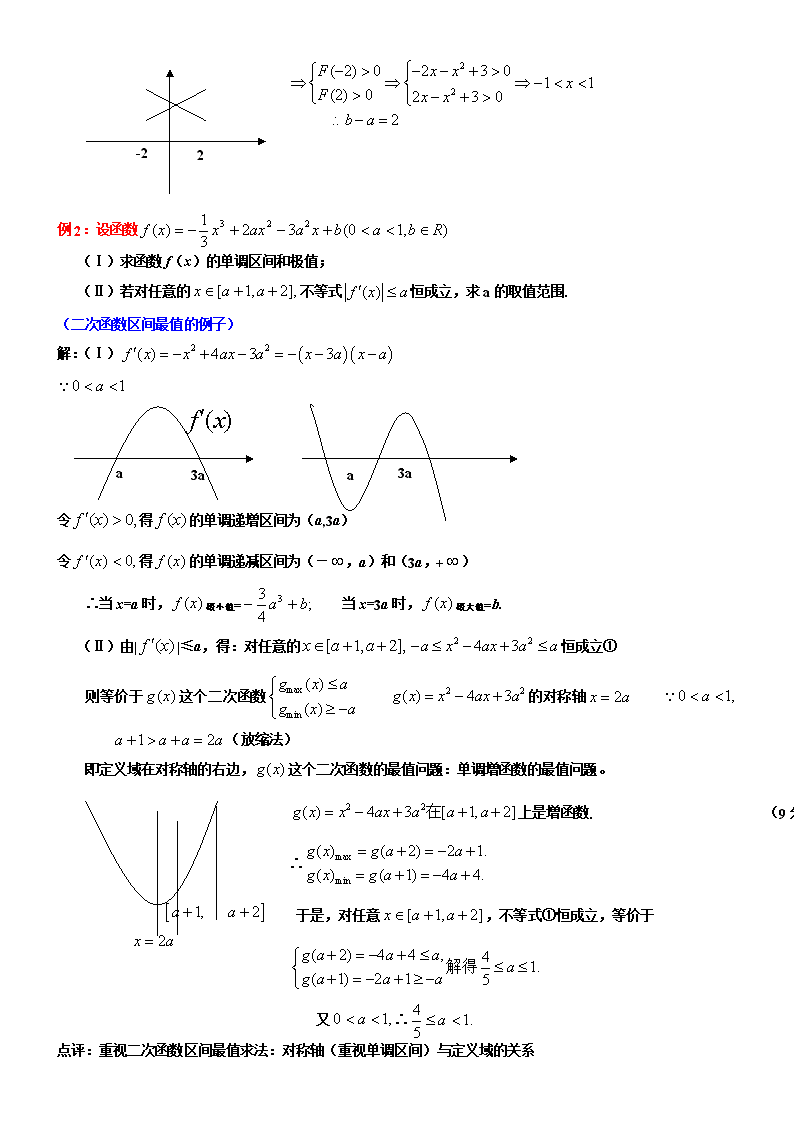例2：设函数 ‎ （Ⅰ）求函数f（x）的单调区间和极值；‎ ‎ （Ⅱ）若对任意的不等式恒成立，求a的取值范围. ‎ ‎（二次函数区间最值的例子）‎ 解：（Ⅰ）‎ ‎ ‎ ‎3a a a ‎3a 令得的单调递增区间为（a,3a）‎ 令得的单调递减区间为（－，a）和（3a，+） ‎ ‎∴当x=a时，极小值= 当x=3a时，极大值=b. ‎ ‎ （Ⅱ）由||≤a，得：对任意的恒成立①‎ 则等价于这个二次函数 的对称轴 （放缩法）‎ 即定义域在对称轴的右边，这个二次函数的最值问题：单调增函数的最值问题。‎ 上是增函数. （9分）‎ ‎∴‎ 于是，对任意，不等式①恒成立，等价于 ‎ ‎ ‎ 又∴‎ 点评：重视二次函数区间最值求法：对称轴（重视单调区间）与定义域的关系 第三种：构造函数求最值 题型特征：恒成立恒成立；从而转化为第一、二种题型 例3；已知函数图象上一点处的切线斜率为，‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）当时，求的值域；‎ ‎（Ⅲ）当时，不等式恒成立，求实数t的取值范围。‎ 解：（Ⅰ）∴， 解得 ‎ ‎（Ⅱ）由（Ⅰ）知，在上单调递增，在上单调递减，在上单调递增 又 ‎ ‎ ∴的值域是 ‎（Ⅲ）令 思路1：要使恒成立，只需，即分离变量 思路2：二次函数区间最值 二、题型一：已知函数在某个区间上的单调性求参数的范围 解法1：转化为在给定区间上恒成立， 回归基础题型 解法2：利用子区间（即子集思想）；首先求出函数的单调增或减区间，然后让所给区间是求的增或减区间的子集； ‎ 做题时一定要看清楚“在（m,n）上是减函数”与“函数的单调减区间是（a,b）”，要弄清楚两句话的区别：前者是后者的子集 例4：已知，函数．‎ ‎（Ⅰ）如果函数是偶函数，求的极大值和极小值；‎ ‎（Ⅱ）如果函数是上的单调函数，求的取值范围．‎ 解：. ‎ ‎ （Ⅰ）∵ 是偶函数，∴ . 此时，， ‎ ‎ 令，解得：. ‎ ‎ 列表如下：‎ ‎(－∞,－2)‎ ‎－2‎ ‎(－2,2)‎ ‎2‎ ‎(2,+∞)‎ ‎+‎ ‎0‎ ‎－‎ ‎0‎ ‎+‎ 递增 极大值 递减 极小值 递增 ‎ 可知：的极大值为， 的极小值为. ‎ ‎ （Ⅱ）∵函数是上的单调函数，‎ ‎∴，在给定区间R上恒成立判别式法 则 解得：. ‎ ‎ 综上，的取值范围是. ‎ 例5、已知函数 ‎ （I）求的单调区间；‎ ‎ （II）若在[0，1]上单调递增，求a的取值范围。子集思想 ‎（I）‎ ‎ 1、‎ ‎ 当且仅当时取“=”号，单调递增。 ‎ ‎ 2、‎ ‎ a-1‎ ‎-1‎ 单调增区间：‎ ‎ 单调减区间：‎ ‎（II）当 则是上述增区间的子集：‎ ‎1、时，单调递增 符合题意 ‎2、， ‎ 综上，a的取值范围是[0，1]。 ‎ 三、题型二：根的个数问题 题1函数f(x)与g(x)（或与x轴）的交点======即方程根的个数问题 解题步骤 第一步：画出两个图像即“穿线图”（即解导数不等式）和“趋势图”即三次函数的大致趋势“是先增后减再增”还是“先减后增再减”；‎ 第二步：由趋势图结合交点个数或根的个数写不等式（组）；主要看极大值和极小值与0的关系；‎ 第三步：解不等式（组）即可；‎ 例6、已知函数，，且在区间上为增函数．‎ （1） 求实数的取值范围；‎ （2） 若函数与的图象有三个不同的交点，求实数的取值范围．‎ 解：（1）由题意 ∵在区间上为增函数，‎ ‎∴在区间上恒成立（分离变量法）‎ 即恒成立，又，∴，故∴的取值范围为 ‎ ‎（2）设，‎ 令得或由（1）知，‎ ‎①当时，，在R上递增，显然不合题意…‎ ‎②当时，，随的变化情况如下表：‎ ‎—‎ ‎↗‎ 极大值 ‎↘‎ 极小值 ‎↗‎ 由于，欲使与的图象有三个不同的交点，即方程有三个不同的实根，故需，即 ∴，解得 综上，所求的取值范围为 根的个数知道，部分根可求或已知。‎ 例7、已知函数 ‎（1）若是的极值点且的图像过原点，求的极值；‎ ‎（2）若，在（1）的条件下，是否存在实数，使得函数的图像与函数的图像恒有含的三个不同交点？若存在，求出实数的取值范围；否则说明理由。高1考1资1源2网 解：（1）∵的图像过原点，则 ，‎ 又∵是的极值点，则 ‎-1‎ ‎ ‎ ‎（2）设函数的图像与函数的图像恒存在含的三个不同交点，‎ 等价于有含的三个根，即：‎ 整理得：‎ 即：恒有含的三个不等实根 ‎（计算难点来了：）有含的根，‎ 则必可分解为，故用添项配凑法因式分解，‎ ‎ 十字相乘法分解：‎ 恒有含的三个不等实根 等价于有两个不等于-1的不等实根。‎ 题2：切线的条数问题====以切点为未知数的方程的根的个数 例7、已知函数在点处取得极小值－4，使其导数的的取值范围为，求：（1）的解析式；（2）若过点可作曲线的三条切线，求实数的取值范围．‎ ‎（1）由题意得：‎ ‎∴在上；在上；在上 因此在处取得极小值 ‎∴①，②，③‎ 由①②③联立得：，∴ ‎ ‎（2）设切点Q，‎ 过 令，‎ 求得：，方程有三个根。‎ 需：‎ 故：；因此所求实数的范围为：‎ 题3：已知在给定区间上的极值点个数则有导函数=0的根的个数 解法：根分布或判别式法 例8、‎ 解：函数的定义域为（Ⅰ）当m＝4时，f (x)＝ x3－x2＋10x，‎ ‎＝x2－7x＋10，令 ， 解得或.‎ 令 ， 解得 可知函数f(x)的单调递增区间为和（5，＋∞），单调递减区间为．‎ ‎（Ⅱ）＝x2－(m＋3)x＋m＋6, ‎ 要使函数y＝f (x)在（1，＋∞）有两个极值点,＝x2－(m＋3)x＋m＋6=0的根在（1，＋∞）‎ ‎1‎ 根分布问题：‎ 则， 解得m＞3‎ 例9、已知函数，（1）求的单调区间；（2）令＝x4＋f（x）（x∈R）有且仅有3个极值点，求a的取值范围．‎ 解：（1） ‎ 当时，令解得，令解得，‎ 所以的递增区间为，递减区间为.‎ 当时，同理可得的递增区间为，递减区间为.‎ ‎（2）有且仅有3个极值点 ‎=0有3个根，则或，‎ 方程有两个非零实根，所以 或 而当或时可证函数有且仅有3个极值点 其它例题：‎ ‎1、（最值问题与主元变更法的例子）.已知定义在上的函数在区间上的最大值是5，最小值是－11.‎ ‎（Ⅰ）求函数的解析式；‎ ‎（Ⅱ）若时，恒成立，求实数的取值范围.‎ 解：（Ⅰ）‎ ‎ 令=0,得 ‎ 因为，所以可得下表：‎ ‎0‎ ‎+‎ ‎0‎ ‎-‎ ‎↗‎ 极大 ‎↘‎ ‎ ‎ 因此必为最大值,∴因此， ，‎ ‎ 即，∴，∴ ‎ ‎（Ⅱ）∵，∴等价于， ‎ 令，则问题就是在上恒成立时，求实数的取值范围，‎ 为此只需，即， ‎ ‎ 解得，所以所求实数的取值范围是[0，1].‎ ‎2、（根分布与线性规划例子）‎ ‎（1）已知函数 ‎(Ⅰ) 若函数在时有极值且在函数图象上的点处的切线与直线平行, 求的解析式；‎ ‎(Ⅱ) 当在取得极大值且在取得极小值时, 设点所在平面区域为S, 经过原点的直线L将S分为面积比为1:3的两部分, 求直线L的方程.‎ 解： (Ⅰ). 由, 函数在时有极值 ,‎ ‎∴ ‎ ‎∵ ∴ ‎ 又∵ 在处的切线与直线平行,‎ ‎∴ 故 ‎ ‎∴ ……………………. 7分 ‎ (Ⅱ) 解法一: 由 及在取得极大值且在取得极小值,‎ ‎∴ 即 令, 则 ‎ ‎∴ ∴ 故点所在平面区域S为如图△ABC, ‎ 易得, , , , , ‎ 同时DE为△ABC的中位线, ‎ ‎∴ 所求一条直线L的方程为: ‎ 另一种情况设不垂直于x轴的直线L也将S分为面积比为1:3的两部分, 设直线L方程为,它与AC,BC分别交于F、G, 则 , ‎ 由 得点F的横坐标为: ‎ 由 得点G的横坐标为: ‎ ‎∴ 即 ‎ 解得: 或 (舍去) 故这时直线方程为: ‎ 综上,所求直线方程为: 或 .…………….………….12分 ‎(Ⅱ) 解法二: 由 及在取得极大值且在取得极小值,‎ ‎∴ 即 令, 则 ‎ ‎∴ ∴ 故点所在平面区域S为如图△ABC, ‎ 易得, , , , , ‎ 同时DE为△ABC的中位线, ∴所求一条直线L的方程为: ‎ 另一种情况由于直线BO方程为: , 设直线BO与AC交于H , ‎ 由 得直线L与AC交点为: ‎ ‎∵ , , ‎ ‎ ∴ 所求直线方程为: 或 ‎ ‎3、（根的个数问题）已知函数的图象如图所示。‎ ‎ （Ⅰ）求的值；‎ ‎（Ⅱ）若函数的图象在点处的切线方程为，求函数f ( x )的解析式；‎ ‎（Ⅲ）若方程有三个不同的根，求实数a的取值范围。‎ 解：由题知：‎ ‎（Ⅰ）由图可知 函数f ( x )的图像过点( 0 , 3 )，且= 0‎ ‎ 得 ‎ ‎（Ⅱ）依题意 = – 3 且f ( 2 ) = 5‎ ‎ 解得a = 1 , b = – 6 ‎ ‎ 所以f ( x ) = x3 – 6x2 + 9x + 3 ‎ ‎（Ⅲ）依题意 f ( x ) = ax3 + bx2 – ( 3a + 2b )x + 3 ( a＞0 ) ‎ ‎ = 3ax2 + 2bx – 3a – 2b 由= 0b = – 9a ①‎ ‎ 若方程f ( x ) = 8a有三个不同的根，当且仅当 满足f ( 5 )＜8a＜f ( 1 ) ②‎ ‎ 由① ② 得 – 25a + 3＜8a＜7a + 3＜a＜3 ‎ ‎ 所以 当＜a＜3时，方程f ( x ) = 8a有三个不同的根。………… 12分 ‎4、（根的个数问题）已知函数 ‎ （1）若函数在处取得极值，且，求的值及的单调区间；‎ ‎ （2）若，讨论曲线与的交点个数．‎ ‎ 解：（1）‎ ‎………………………………………………………………………2分 令得 令得 ‎∴的单调递增区间为，，单调递减区间为…………5分 ‎（2）由题得 即 令……………………6分 令得或……………………………………………7分 当即时 ‎－‎ 此时，，，有一个交点；…………………………9分 当即时，‎ ‎ ‎ ‎ ‎ ‎＋‎ ‎—‎ ‎ ‎ ‎,‎ ‎∴当即时,有一个交点；‎ 当即时，有两个交点；‎ ‎ 　 当时，，有一个交点．………………………13分 综上可知，当或时，有一个交点；‎ ‎ 当时，有两个交点．…………………………………14分