天津高考文科数学及答案 11页

‎2010年普通高等学校招生全国统一考试（天津卷）‎ 数 学(文史类)‎ 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试用时120分钟。第I卷1至3页。第Ⅱ卷4至11页。考试结束后，将本试卷和答题卡一并交回。‎ 祝各位考生考试顺利！‎ 第I卷 注意事项：‎ ‎1．答I卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码。‎ ‎2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答在试卷上的无效。‎ ‎ 3．本卷共10小题，每小题5分，共50分。‎ 参考公式：‎ 如果事件互斥，那么 棱柱的体积公式V=Sh.‎ ‎ 其中S表示棱柱的底面积.‎ ‎ h表示棱柱的高 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。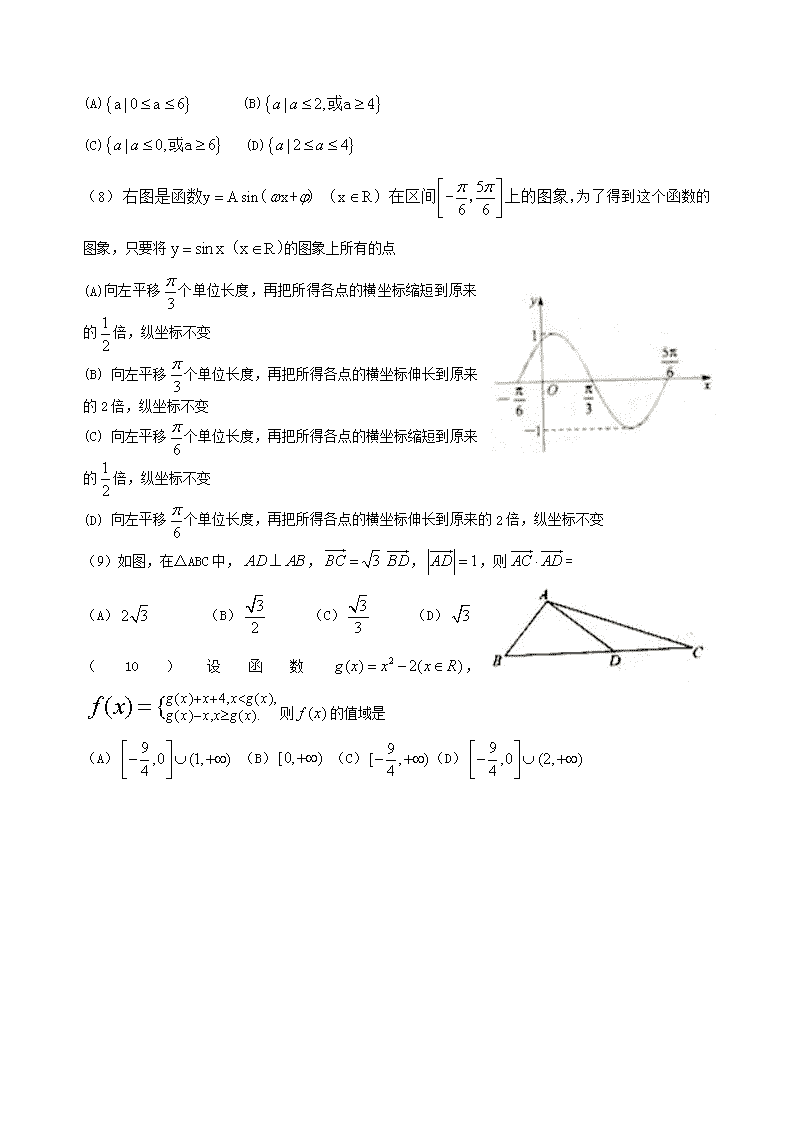‎ ‎(1)i是虚数单位，复数=‎ ‎(A)1+2i (B)2+4i (C)-1-2i (D)2-i ‎(2)设变量x，y满足约束条件则目标函数z=4x+2y的最大值为 ‎（A）12 （B）10 （C）8 （D）2‎ ‎(3)阅读右边的程序框图，运行相应的程序，则输出s的值为 ‎ (A)-1 (B)0 (C)1 (D)3‎ ‎（4）函数f（x）=‎ ‎ (A)（-2,-1） (B) （-1,0） (C) （0,1） (D) （1,2）‎ ‎(5)下列命题中，真命题是 ‎(A)‎ ‎(B)‎ ‎(C)‎ ‎(D)‎ ‎(6)设 ‎(A)a0. ‎ ‎（Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；‎ ‎（Ⅱ）若在区间上，f（x）>0恒成立，求a的取值范围.‎ ‎（21）（本小题满分14分）‎ 已知椭圆（a>b>0）的离心率e=，连接椭圆的四个顶点得到的菱形的面积为4.‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设直线l与椭圆相交于不同的两点A、B，已知点A的坐标为（-a，0）.‎ ‎ （i）若，求直线l的倾斜角；‎ ‎ （ii）若点Q在线段AB的垂直平分线上，且.求的值.‎ ‎（22）（本小题满分14分）‎ 在数列中，=0，且对任意k，成等差数列，其公差为2k.‎ ‎（Ⅰ）证明成等比数列；‎ ‎（Ⅱ）求数列的通项公式；‎ ‎（Ⅲ）记，证明.‎ ‎2010年普通高等学校招生全国统一考试（天津卷）‎ 数学（文史类）参考答案 一. 选择题：本题考查基本知识和基本运算，每小题5分，满分50分.‎ ‎（1）A (2)B (3)B (4)C (5)A ‎（6）D (7)C (8)A (9)D (10)D 二. 填空题：本题考查基本知识和基本运算，每小题4分，满分24分.‎ ‎（11） (12)3 (13) ‎ ‎（14） (15)4 (16) ‎ 三. 解答题 ‎（17）本小题主要考查正弦定理、两角和与差的正弦、同角三角函数的基本关系、二倍角的正弦与余弦等基础知识，考查基本运算能力.满分12分.‎ ‎ （Ⅰ）证明：在△ABC中，由正弦定理及已知得=.于是sinBcosC-cosBsinC=0，即sin（B-C）=0.因为，从而B-C=0.‎ ‎ 所以B=C.‎ ‎ （Ⅱ）解：由A+B+C=和（Ⅰ）得A=-2B,故cos2B=-cos（-2B）=-cosA=.‎ 又0<2B<,于是sin2B==.‎ ‎ 从而sin4B=2sin2Bcos2B=，cos4B=.‎ ‎ 所以 ‎（18）本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分 ‎ （Ⅰ）解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P（A）==.‎ ‎ （Ⅱ）（i）解：一等品零件的编号为.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,‎ ‎,,,共有15种.‎ ‎ (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”（记为事件B）的所有可能结果有：‎ ‎，，共有6种.‎ ‎ 所以P(B)=.‎ ‎(19)本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识，考查空间想象能力，运算能力和推理论证能力.满分12分.‎ ‎(I)解：因为四边形ADEF是正方形，所以FA//ED.故为异面直线CE与AF所成的角.‎ 因为FA平面ABCD，所以FACD.故EDCD.‎ 在Rt△CDE中，CD=1，ED=，CE==3,故cos==.‎ 所以异面直线CE和AF所成角的余弦值为.‎ ‎(Ⅱ)证明：过点B作BG//CD,交AD于点G，则.由,可得BGAB,从而CDAB,又CDFA,FAAB=A,所以CD平面ABF.‎ ‎(Ⅲ)解：由（Ⅱ）及已知，可得AG=，即G为AD的中点.取EF的中点N，连接GN，则GNEF,因为BC//AD,所以BC//EF.过点N作NMEF，交BC于M，则为二面角B-EF-A的平面角。‎ 连接GM，可得AD平面GNM,故ADGM.从而BCGM.由已知，可得GM=.由NG//FA,FAGM,得NGGM.‎ 在Rt△NGM中，tan,‎ 所以二面角B-EF-A的正切值为. (20)本小题主要考查曲线的切线方程、利用导数研究函数的单调性与极值、解不等式等基础知识，考查运算能力及分类讨论的思想方法.满分12分.‎ ‎（Ⅰ）解：当a=1时，f（x）=，f（2）=3；f’(x)=, f’(2)=6.所以曲线y=f（x）在点（2，f（2））处的切线方程为y-3=6（x-2），即y=6x-9.‎ ‎（Ⅱ）解：f’(x)=.令f’(x)=0，解得x=0或x=.‎ 以下分两种情况讨论：‎ （1） 若，当x变化时，f’(x)，f（x）的变化情况如下表：‎ X ‎0‎ f’(x)‎ ‎+‎ ‎0‎ ‎-‎ f(x)‎ 极大值 ‎ 当等价于 ‎ 解不等式组得-52，则.当x变化时，f’(x),f（x）的变化情况如下表：‎ X ‎0‎ f’(x)‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ f(x)‎ 极大值 极小值 当时，f（x）>0等价于即 解不等式组得或.因此2