上海地区高考数学总复习专题2排列组合二项式定理算法分项练习含解析 5页

第十二章 排列组合、二项式定理 一．基础题组 ‎1. 【2017高考上海，2】若排列数 ，则 .‎ ‎【答案】3‎ ‎【解析】由排列数的定义： ，则： ，解得 .‎ ‎2.【2016高考上海理数】在的二项展开式中，所有项的二项式系数之和为256，则常数项等于_________．‎ ‎【答案】112‎ ‎【解析】试题分析：‎ ‎【考点】二项式定理 ‎【名师点睛】根据二项展开式的通项，确定二项式系数或确定二项展开式中的指定项，是二项式定理问题中的基本问题，往往要综合运用二项展开式的系数的性质、二项展开式的通项进行求解. 本题能较好地考查考生的思维能力、基本计算能力等.‎ ‎3.【2015高考上海理数】在报名的名男教师和名女教师中，选取人参加义务献血，要求男、女教师都有，则不同的选取方式的种数为 （结果用数值表示）．‎ ‎【答案】‎ ‎【解析】由题意得，去掉选5名女教师情况即可：‎ ‎【考点定位】排列组合 ‎【名师点睛】涉及排列与组合问题，区分的关键是看选出的元素是否与顺序有关，排列问题与顺序有关，组合问题与顺序无关．“含”与“不含”的问题：“含”，则先将这些元素取出，再由另外元素补足；“不含”，则先将这些元素剔除，再从剩下的元素中去选取．通常用直接法分类复杂时，考虑逆向思维，用间接法处理．‎ ‎4、【2015高考上海理数】在的展开式中，项的系数为 （结果用数值表示）．‎ ‎【答案】‎ ‎【解析】因为，所以项只能在展开式中，即为，系数为 ‎【考点定位】二项展开式 ‎【名师点睛】（1）求二项展开式中的指定项，一般是利用通项公式进行化简通项公式后，令字母的指数符合要求 (求常数项时，指数为零；求有理项时，指数为整数等)，解出项数r＋1，代回通项公式即可．（2）对于三项式问题一般先变形化为二项式再解决．‎ ‎5.【2015高考上海文数】.在的二项式中，常数项等于 （结果用数值表示）.‎ ‎【答案】240‎ ‎【考点定位】二项式定理.‎ ‎【名师点睛】求二项展开式中的指定项，一般是利用通项公式进行，化简通项公式后，令字母的指数符合要求(求常数项时，指数为零；求有理项时，指数为整数等)．‎ ‎6. 【2013上海,理5】设常数a∈R.若的二项展开式中x7项的系数为－10，则a＝______.‎ ‎【答案】－2　‎ ‎【解析】Tr＋1＝,2(5－r)－r＝7r＝1，故＝－‎10a＝－2.‎ ‎7. 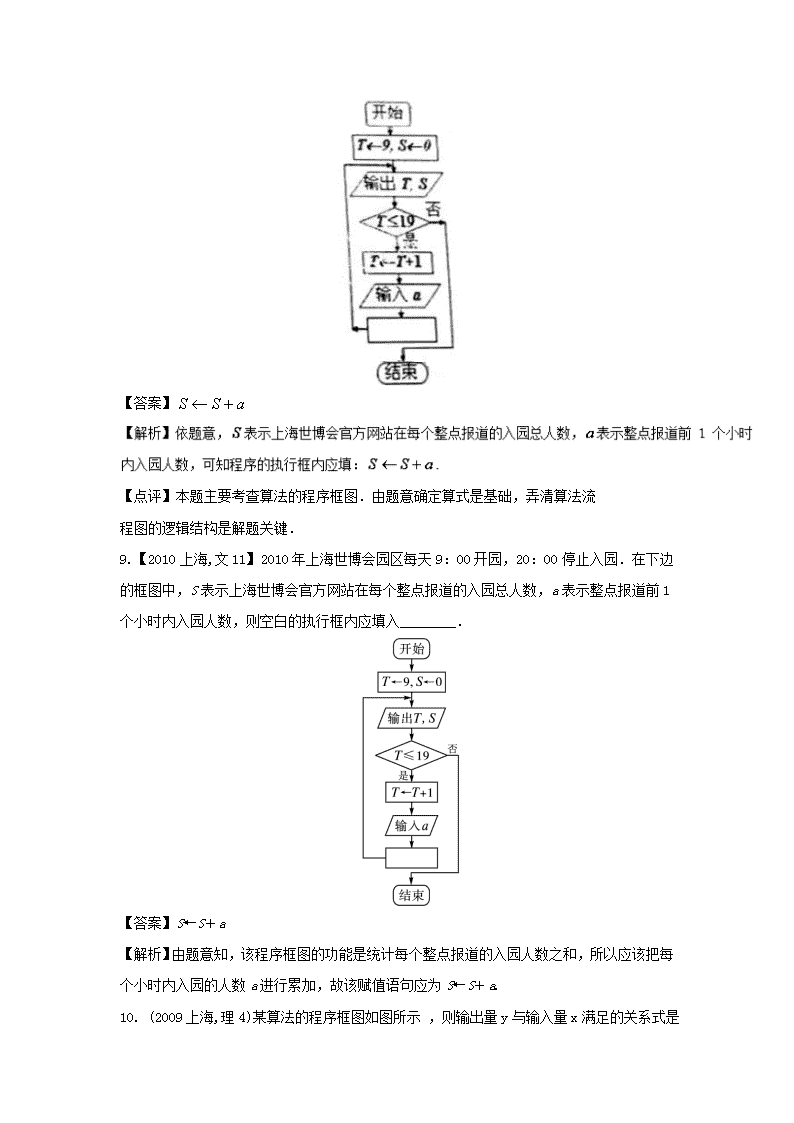【2012上海,理5】在(x－)6的二项展开式中，常数项等于__________．‎ ‎【答案】－160‎ ‎【解析】(x－)6的二项展开式中的常数项为·(x)3·(－)3＝－160.‎ ‎8. 【2010上海,理7】2010年上海世博会园区每天9:00开园，20:00停止入园。在右边的框图中，表示上海世博会官方网站在每个整点报道的入园总人数，表示整点报道前1个小时内入园人数，则空白的执行框内应填入 ；‎ ‎【答案】‎ ‎【点评】本题主要考查算法的程序框图．由题意确定算式是基础，弄清算法流 程图的逻辑结构是解题关键．‎ ‎9. 【2010上海,文11】 2010年上海世博会园区每天9：00开园，20：00停止入园．在下边的框图中，S表示上海世博会官方网站在每个整点报道的入园总人数，a表示整点报道前1个小时内入园人数，则空白的执行框内应填入________．‎ ‎【答案】S←S＋a ‎【解析】由题意知，该程序框图的功能是统计每个整点报道的入园人数之和，所以应该把每个小时内入园的人数a进行累加，故该赋值语句应为S←S＋a. ‎ ‎10. (2009上海,理4)某算法的程序框图如图所示 ‎ ，则输出量y与输入量x满足的关系式是___________.‎ ‎【答案】‎ ‎11. (2009上海,文4)某算法的程序框图如图所示 ，则输出量y与输入量x满足的关系式是 ‎___________.‎ ‎【答案】‎ ‎【解析】由程序框图可知,当输入实数满足x＞1时,输出y=x-2;‎ 否则,即输入实数满足x≤1时,‎ 输出y=2x.综上可知 ‎12. 【2008上海,理12】‎ ‎ ‎ ‎【答案】‎ ‎【解析】由. ‎ ‎13. 【2005上海,理4】在的展开式中，的系数是15，则实数=__________.‎ ‎【答案】‎ ‎【解析】的系数