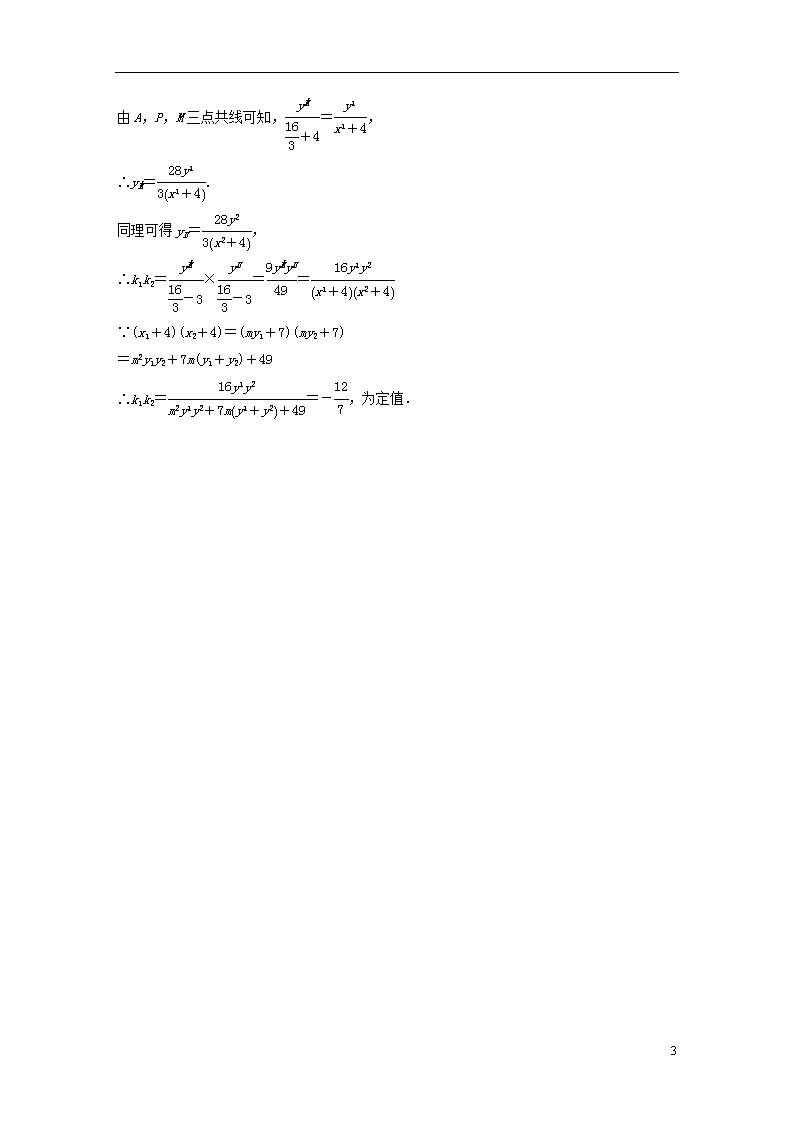2020高考数学二轮复习 专题四 解析几何 规范答题示例7 解析几何中的探索性问题学案 3页

规范答题示例7　解析几何中的探索性问题 典例7　(15分)已知定点C(－1,0)及椭圆x2＋3y2＝5，过点C的动直线与椭圆相交于A，B两点．‎ ‎(1)若线段AB中点的横坐标是－，求直线AB的方程；‎ ‎(2)在x轴上是否存在点M，使·为常数？若存在，求出点M的坐标；若不存在，请说明理由．‎ 审题路线图　(1)→→ ‎(2)→→→ 规 范 解 答·分 步 得 分 构 建 答 题 模 板 解　(1)依题意，直线AB的斜率存在，设直线AB的方程为y＝k(x＋1)，‎ 将y＝k(x＋1)代入x2＋3y2＝5，消去y整理得(3k2＋1)x2＋6k2x＋3k2－5＝0.3分 设A(x1，y1)，B(x2，y2)，则 由线段AB中点的横坐标是－，得 ＝－＝－，解得k＝±，适合①.‎ 所以直线AB的方程为x－y＋1＝0或x＋y＋1＝0.6分 ‎(2)假设在x轴上存在点M(m,0)，使·为常数．‎ ‎(ⅰ)当直线AB与x轴不垂直时，由(1)知x1＋x2＝－，x1x2＝. ③‎ 所以·＝(x1－m)(x2－m)＋y1y2＝(x1－m)(x2－m)＋k2(x1＋1)(x2＋1)‎ ‎＝(k2＋1)x1x2＋(k2－m)(x1＋x2)＋k2＋m2.9分 将③代入，整理得·＝＋m2＝＋m2＝m2＋‎2m－－.11分 第一步 先假定：假设结论成立．‎ 第二步 再推理：以假设结论成立为条件，进行推理求解．‎ 第三步 下结论：若推出合理结果，经验证成立则肯定假设；若推出矛盾则否定假设．‎ 第四步 再回顾：查看关键点，易错点(特殊情况、隐含条件等)，审视解题规范性.‎ 3‎ 注意到·是与k无关的常数，‎ 从而有‎6m＋14＝0，解得m＝－，此时·＝.12分 ‎(ⅱ)当直线AB与x轴垂直时，此时点A，B的坐标分别为，，当m＝－时，也有·＝.14分 综上，在x轴上存在定点M，使·为常数.15分 评分细则　(1)不考虑直线AB斜率不存在的情况扣1分；‎ ‎(2)不验证Δ>0，扣1分；‎ ‎(3)直线AB方程写成斜截式形式同样给分；‎ ‎(4)没有假设存在点M不扣分；‎ ‎(5)·没有化简至最后结果扣1分，没有最后结论扣1分．‎ 跟踪演练7　已知椭圆C：＋＝1(a>b>0)的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线x－y＋12＝0相切．‎ ‎(1)求椭圆C的方程；‎ ‎(2)设A(－4,0)，过点R(3,0)作与x轴不重合的直线l交椭圆C于P，Q两点，连接AP，AQ分别交直线x＝于M，N两点，若直线MR，NR的斜率分别为k1，k2，试问：k1k2是否为定值？若是，求出该定值，若不是，请说明理由．‎ 解　(1)由题意得　∴ 故椭圆C的方程为＋＝1.‎ ‎(2)设直线PQ的方程为x＝my＋3，‎ P(x1，y1)，Q(x2，y2)，M，N.‎ 由 得(‎3m2‎＋4)y2＋18my－21＝0，‎ 且Δ＝(‎18m)2＋84(‎3m2‎＋4)>0，‎ ‎∴y1＋y2＝，y1y2＝.‎ 由A，P，M三点共线可知，＝，‎ 3‎ ‎∴yM＝.‎ 同理可得yN＝，‎ ‎∴k1k2＝×＝＝ ‎∵(x1＋4)(x2＋4)＝(my1＋7)(my2＋7)‎ ‎＝m2y1y2＋‎7m(y1＋y2)＋49‎ ‎∴k1k2＝＝－，为定值．‎ 3‎