历年高考不等式专题及解析 7页

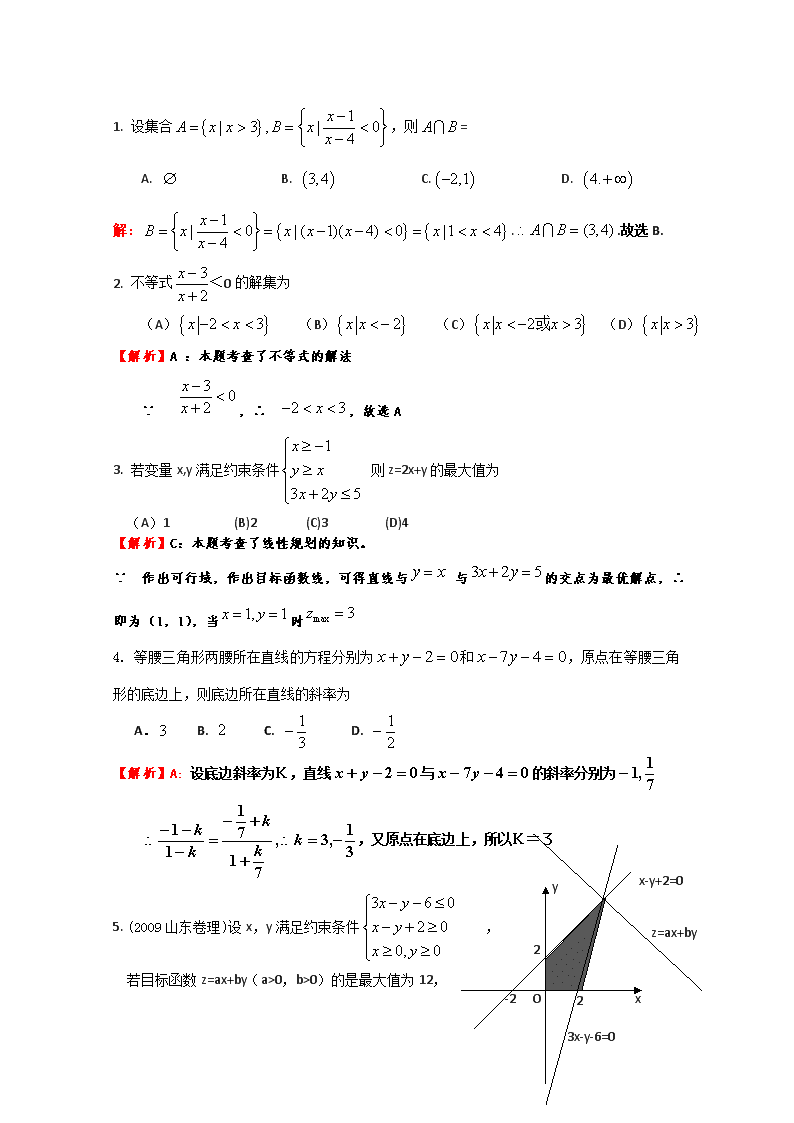
‎1. 设集合，则=‎ ‎ A. B. C. D. ‎ 解：..故选B.‎ ‎2. 不等式＜0的解集为 ‎（A） （B） （C） （D）‎ ‎【解析】A ：本题考查了不等式的解法 ‎ ∵ ，∴ ，故选A ‎3. 若变量x,y满足约束条件 则z=2x+y的最大值为 ‎（A）1 (B)2 (C)3 (D)4‎ ‎【解析】C：本题考查了线性规划的知识。‎ ‎∵ 作出可行域，作出目标函数线，可得直线与 与的交点为最优解点，∴即为（1，1），当时 ‎4. 等腰三角形两腰所在直线的方程分别为和，原点在等腰三角形的底边上，则底边所在直线的斜率为 A． B. C. D. ‎ ‎【解析】A: 设底边斜率为Ｋ，直线与的斜率分别为 ‎　　，又原点在底边上，所以Ｋ＝３‎ x ‎ ‎2 ‎ ‎2 ‎ y ‎ O ‎ ‎-2 ‎ z=ax+by ‎ ‎3x-y-6=0 ‎ x-y+2=0 ‎ ‎5. (2009山东卷理)设x，y满足约束条件 ，‎ 若目标函数z=ax+by（a>0，b>0）的是最大值为12，‎ 则的最小值为 ( ). ‎ A. B. C. D. 4‎ 答案： A 解析 不等式表示的平面区域如图所示阴影部分,当直线ax+by= z（a>0，b>0）‎ 过直线x-y+2=0与直线3x-y-6=0的交点（4,6）时,‎ 目标函数z=ax+by（a>0，b>0）取得最大12,‎ 即4a+6b=12,即2a+3b=6, 而=,故选A.‎ ‎6.（2009安徽卷理）若不等式组所表示的平面区域被直线分为面积相等的两部分，则的值是 ‎ A. B. C. D. ‎ 答案: B A x D y C O y=kx+‎ 解析 不等式表示的平面区域如图所示阴影部分△ABC 由得A（1，1），又B（0，4），C（0，）‎ ‎∴△ABC=，设与的 交点为D，则由知，∴‎ ‎∴选A。 ‎ ‎7.（2009宁夏海南卷文）设满足则 A.有最小值2，最大值3 B.有最小值2，无最大值 C.有最大值3，无最小值 D.既无最小值，也无最大值 ‎ 答案: B 解析 画出不等式表示的平面区域，如右图，由z＝x＋y，得y＝－x＋z，令z＝0，画出y＝－x的图象，当它的平行线经过A（2,0）时，z取得最小值，最小值为：z＝2，无最大值，故选.B ‎8. 不等式的解集为 . ‎ 答案 : ‎ 解析 原不等式等价于不等式组①或②‎ 或③不等式组①无解,由②得,由③得,综上得,所以原不等式的解集为. 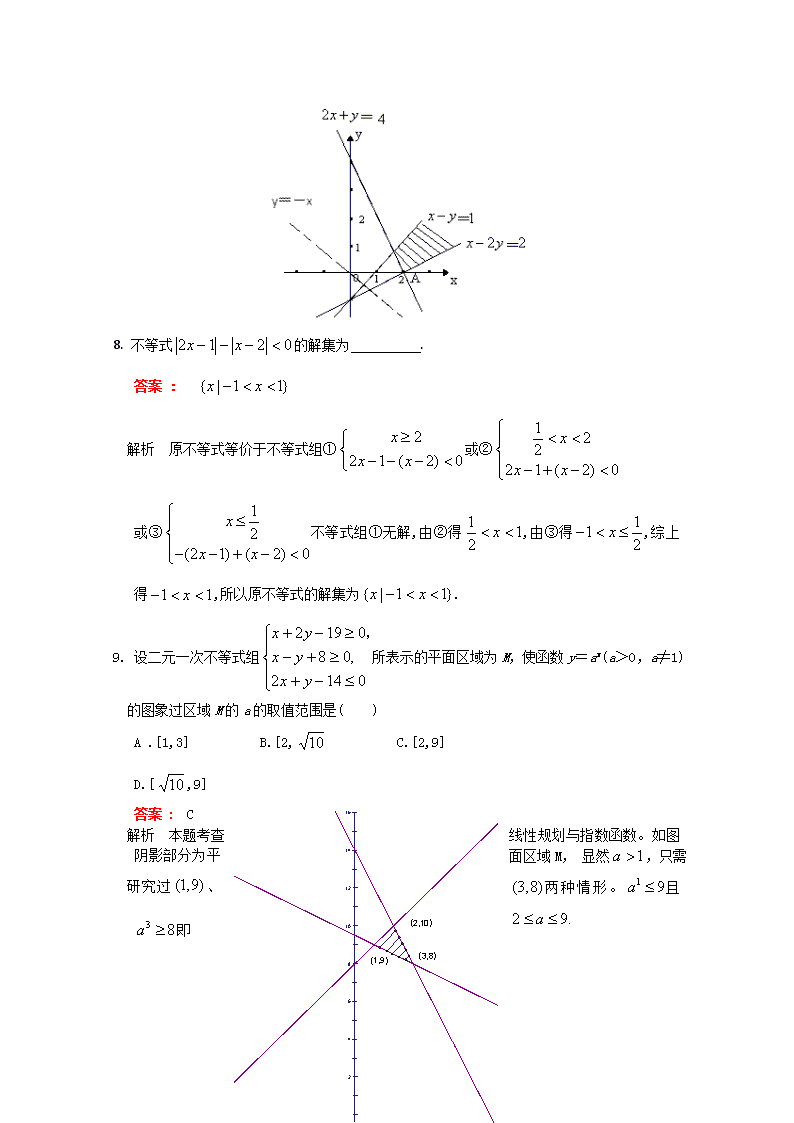‎ ‎9. 设二元一次不等式组所表示的平面区域为M，使函数y＝ax(a＞0，a≠1)的图象过区域M的a的取值范围是( )‎ A .[1,3] B.[2, C.[2,9] ‎ D.[,9]‎ 答案 : C 解析 本题考查线性规划与指数函数。如图阴影部分为平面区域M， 显然，只需 研究过、两种情形。且即 ‎10. 下列选项中，p是q的必要不充分条件的是 ‎ A.p:＞b+d , q:＞b且c＞d ‎ B.p:a＞1,b>1 q:的图像不过第二象限 ‎ C.p: x=1, q: ‎ D.p:a＞1, q: 在上为增函数 ‎ 答案 : A 解析 由＞b且c＞d＞b+d，而由＞b+d ＞b且c＞d，可举反例。选A。‎ ‎11. “”是“且”的 ‎ A. 必要不充分条件 B. 充分不必要条件 ‎ C. 充分必要条件 D. 既不充分也不必要条件 答案: A 解析 易得时必有.若时，则可能有，选A。‎ ‎12. 已知，，，为实数，且＞.则“＞”是“－＞－”的 ‎ A. 充分而不必要条件 B. 必要而不充分条件 ‎ C. 充要条件 D. 既不充分也不必要条件 答案: B ‎ 解析 显然，充分性不成立.又，若－＞－和＞都成立，则同向不等式相加得＞‎ ‎ 即由“－＞－”“＞”‎ ‎13. 已知为实数，且。则“”是“”的 A. 充分而不必要条件 B. 必要而不充分条件 ‎ C．充要条件 D. 既不充分也不必要条件 ‎ 答案: B 解析 推不出；但，故选择B。‎ 解析2：令，则；由可得，因为，则，所以。故“”是“”的必要而不充分条件。‎ ‎14. 不等式对任意实数恒成立，则实数的取值范围为（ ）‎ A． B． ‎ C． D．‎ 答案: A 解析 因为对任意x恒成立，所以 ‎15. 设，若，则下列不等式中正确的是（ ）‎ A、 B、 C、 D、‎ 答案: D 解析 利用赋值法：令排除A,B,C,选D ‎ ‎16. 不等式的解集是 （ ）‎ A． B． C． D．‎ 答案: D 解：由得：，即，故选D ‎17. 若a>0，b>0，则不等式－b< D.x<或x>‎ 答案: D 解析 故选D ‎18. 不等式的解集为　　‎ 答案: ‎ 解析 ，0〈，.‎ 解得 ‎－2‎ x y O ‎19. 已知函数f(x)的定义域为[－2，+∞)，部分对应值如下表,为f (x)的导函数，函数的图象如右图所示，若两正数a，b满足，则的取值范围是　 　．‎ 答案: ‎ x ‎2‎ ‎0‎ ‎4‎ f (x)‎ ‎1‎ ‎－1‎ ‎1‎ ‎20. 记关于的不等式的解集为，不等式的解集为．‎ ‎（I）若，求；‎ ‎（II）若，求正数的取值范围．‎ 解：（I）由，得．‎ ‎（II）．‎ 由，得，又，所以，‎ 即的取值范围是．‎ ‎21. 设p:实数x满足,其中,命题实数满足.‎ ‎(Ⅰ)若且为真，求实数的取值范围；‎ ‎(Ⅱ)若是的充分不必要条件,求实数的取值范围. ‎ 解: 由得，‎ 又,所以, ‎ 当时，1<,即为真时实数的取值范围是1<. ‎ 由,得,即为真时实数的取值范围是. ‎ 若为真，则真且真，‎ 所以实数的取值范围是. ‎ ‎(Ⅱ) 是的充分不必要条件，即,且, ‎ 设A=,B=,则,‎ 又A==, B==}，‎ 则0<,且 所以实数的取值范围是. ‎ www.ks5u.com