（浙江专版）2020年高考数学一轮复习 解三角形及其应用举例 10页

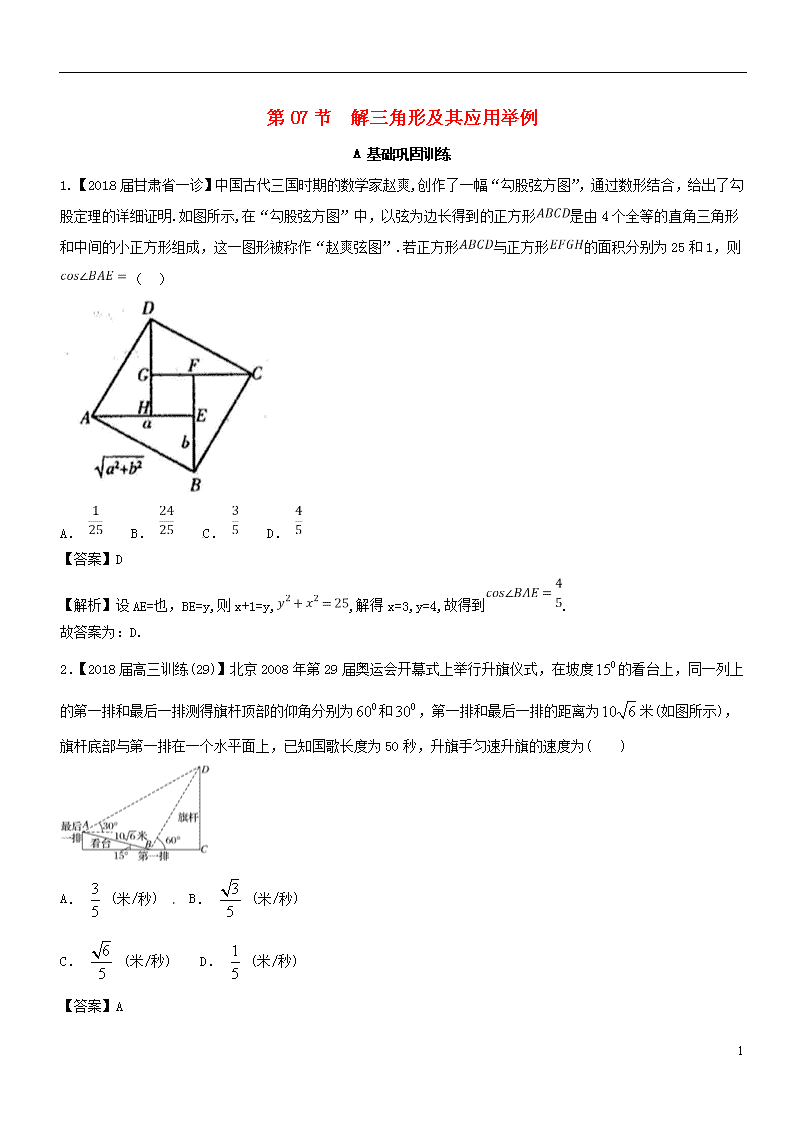
第07节 解三角形及其应用举例 A 基础巩固训练 ‎1.【2018届甘肃省一诊】中国古代三国时期的数学家赵爽,创作了一幅“勾股弦方图”，通过数形结合，给出了勾股定理的详细证明.如图所示,在“勾股弦方图”中，以弦为边长得到的正方形是由4个全等的直角三角形和中间的小正方形组成，这一图形被称作“赵爽弦图”.若正方形与正方形的面积分别为25和1，则（ ）‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】设AE=也，BE=y,则x+1=y,,解得x=3,y=4,故得到.‎ 故答案为：D.‎ ‎2．【2018届高三训练(29)】北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为和，第一排和最后一排的距离为米(如图所示)，旗杆底部与第一排在一个水平面上，已知国歌长度为50秒，升旗手匀速升旗的速度为(　　)‎ A． (米/秒) B． (米/秒)‎ C． (米/秒) D． (米/秒)‎ ‎【答案】A 10‎ ‎3. 要测量顶部不能到达的电视塔的高度, 在点测得塔顶的仰角是,在点测得塔顶的仰角是,并测得水平面上的，则电视塔的高度为（ ） ‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 根据题意，设，则中， ，可得，同理可得中， ， 在中， ， 由余弦定理得， ，整理得： ，解之得或（舍），即电视塔的高度为米，故选D.‎ ‎4．两灯塔与海洋观察站的距离都为，灯塔在的北偏东，在的南偏东，则两灯塔之间距离为( )‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】根据题意画出图形，如图所示：‎ 10‎ 易得∠ACB=90°，AC=BC=a.‎ 在△ABC中，由勾股定理，得AB2=AC2+BC2=‎2a2，‎ 所以AB=（km）.‎ 故选C .‎ ‎5．一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进‎100 m到达点B，在B点测得水柱顶端的仰角为30°，则水柱的高度是(　　)‎ A．‎50 m B．‎‎100 m C．‎120 m D．‎‎150 m ‎【答案】A ‎【解析】设水柱高度是h m，水柱底端为C，则在△ABC中，A＝60°，AC＝h，AB＝100，BC＝h，‎ 根据余弦定理得，(h)2＝h2＋1002－2·h·100·cos 60°，即h2＋50h－5 000＝0，即(h－50)(h＋100)＝0，即h＝50，故水柱的高度是‎50 m.‎ ‎ B能力提升训练 ‎1．如下图所示，在河岸AC测量河的宽度BC，图中所标的数据a，b，c，α，β是可供测量的数据．下面给出的四组数据中，对测量河宽较适宜的是(　　)‎ A．c和α B．c和b C．c和β D．b和α ‎ ‎【答案】D 10‎ ‎【解析】根据直角三角形的特征，只要知道一条边和一个夹角即可求出河宽.‎ ‎2．【2015高考湖北】如图，一辆汽车在一条水平的公路上向正西行驶，到处时测得公路北侧一山顶D在西偏北的方向上，行驶‎600m后到达处，测得此山顶在西偏北的方向上，仰角为，则此山的高度 m. ‎ ‎【答案】‎ ‎3．轮船A和轮船B在中午12时离开海港C，两艘轮船航行方向的夹角为120°，轮船A的航行速度是25海里/小时，轮船B的航行速度是15海里/小时，下午2时两船之间的距离是(　　)‎ A．35海里 B．35海里 C．35海里 D．70海里 ‎【答案】D ‎【解析】设轮船A、B航行到下午2时时所在的位置分别是E、F，则依题意有CE＝25×2＝50，CF＝15×2＝30，且∠ECF＝120°，EF＝＝＝70.‎ ‎4.【2019届高考全程训练月考二】某观测站在目标的南偏西方向，从出发有一条南偏东走向的公路，在处测得与相距的公路处有一个人正沿着此公路向走去，走到达，此时测得距离为，若此人必须在分钟内从处到达处，则此人的最小速度为(　　)‎ 10‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】由已知得∠CAB＝25°＋35°＝60°，BC＝31，CD＝21，BD＝20，可得，那么，‎ 于是在△ABC中， ＝24，‎ 在△ABC中，BC2＝AC2＋AB2－‎2AC·ABcos60°，即312＝242＋AB2－24AB，解得AB＝35或AB＝－11(舍去)，因此AD＝AB－BD＝35－20＝15.‎ 故此人在D处距A处还有‎15 km，若此人必须在20分钟，即小时内从D处到达A处，则其最小速度为15÷＝45(km/h)．‎ 故选B.‎ ‎5．【2017山西三区八校二模】为了竖一块广告牌，要制造三角形支架，如图，要求， 的长度大于‎1米，且比长‎0.5米，为了稳固广告牌，要求越短越好，则最短为（ ）‎ A. 米 B. 米 C. 米 D. 米 ‎【答案】D 10‎ C思维扩展训练 1. 如图：D， C，B三点在地面同一直线上，DC＝，从C，D两点测得A点仰角分别是，()，则A点离地面的高度AB等于( ) ‎ ‎（A） （B） ‎ ‎（C） （D） ‎ ‎【答案】A ‎【解析】因为，所以.‎ ‎2.【2018届赣州二模】如图所示，为了测量，处岛屿的距离，小明在处观测，，分别在处的北偏西、北偏东方向，再往正东方向行驶40海里至处，观测在处的正北方向，在处的北偏西方向，则，两处岛屿间的距离为（ ）‎ 10‎ A． 海里 B． 海里 C． 海里 D． 40海里 ‎【答案】A ‎【解析】在中，，所以，‎ 由正弦定理可得：，解得，‎ 在中，，所以，‎ 在中，由余弦定理可得：‎ ‎，解得.‎ ‎3.【2017安徽马鞍山二模】在边长为2的正三角形的边上分别取两点，点关于线段的对称点正好落在边上，则长度的最小值为____．‎ ‎【答案】‎ ‎【解析】显然两点关于折线对称，连接，可得，则有，设， ，再设，则有，在中， ， ，又，在中，由正弦定理知，即， ，所以当时，即时， ，此时取得最小值，且，则的最小值为，故答案为.‎ ‎4.如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若,则的最大值 .‎ 10‎ ‎【答案】‎ ‎【解析】由勾股定理可得，，过作，交于，连结，则，设，则，由得，，在直角中，，故，令，，令得，，代入得，，故的最大值为．‎ ‎5. 【2018届江苏海安上学期第一次测试】如图，已知是一幢6层的写字楼，每层高均为‎3m，在正前方‎36m处有一建筑物，从楼顶处测得建筑物的张角为.‎ ‎（1）求建筑物的高度；‎ ‎（2）一摄影爱好者欲在写字楼的某层拍摄建筑物.已知从摄影位置看景物所成张角最大时，拍摄效果最佳.问：该摄影爱好者在第几层拍摄可取得最佳效果（不计人的高度）？‎ 10‎ ‎【答案】(1)‎30米;(2) 当时，张角最大，拍摄效果最佳.‎ ‎【解析】试题分析：（1）先作于，构造直角三角形，然后运用两角差的正切公式求出，再求出；（2）先依据题设求出，，然后建立目标函数，通过求函数的最值使得问题获解：‎ 解：（1）如图，作于，则.‎ 所以，.‎ 因为，‎ 所以.‎ 所以.‎ 答：建筑物的高度为‎30米.‎ 因为函数在上是单调增函数，‎ 所以当时，张角最大，拍摄效果最佳.‎ 10‎ 答：该人在6层拍摄时效果最好.‎ 10‎