广西2014高考数学压轴卷试题目文 9页

‎2014广西高考压轴卷文科数学 一、选择题：（每小题5分，共60分）‎ ‎1、若集合，，则等于 （　B　）‎ A． B． C． D． ‎ ‎ 2、若A={2，3，4}，B={x|x=mn，m、n∈A且m≠n}，则集合B的非空真子集有（　 ）个。‎ A．3‎ B．6‎ C．7‎ D．8‎ ‎3、已知命题p：“若直线ax+y+1=0与直线ax-y+2=0垂直，则a=‎1”‎；命题q：“是a＞b”的充要条件，则（　 ）‎ A．p真q假 B．p且q真 C．p或q真 D．p或q假 ‎4、函数y=2+的反函数为（ ）‎ A、 B、‎ C、 D、‎ ‎5、若直线与直线平行，为非零向量，则必有（ ）‎ A、 B、 C、 D、‎ ‎6、已知数列{}为等差数列，且的值为（ ）‎ A、 B、 C、 D、‎ ‎7、现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为（ ）‎ A、232 B、252 C、472 D、484‎ ‎8、将抛物线按平移后所得的抛物线的焦点坐标为（ ）‎ A、 B、 C、 D、‎ ‎9、已知平面直角坐标系xoy上的区域D由不等式组给出，若M（x,y）为D 上的动点，点A(2,-1)，则的最小值为（ ）‎ A、 B 、 C、 D、‎ A B C D E ‎10、如图所示，在等腰梯形ABCD中，AB=2DC=2，，E为AB的中点，将与分别沿ED，EC向上翻折，使A,B重合，则形成的三棱锥的外接球的体积为（ ）‎ A、 B、 ‎ ‎ C、 D、‎ ‎11、设抛物线C的方程,O为坐标原点，P为抛物线的准线与其对称轴的交点，过焦点F且垂直于x轴的直线交抛物线于M,N两点，若直线PM与ON相交于点Q，则( )‎ A、 B、 C、 D、‎ ‎12、已知是定义在R上的不恒为零的函数，且对于任意满足考察下列结论：① ②为偶函数 ③数列为等比数列 ④数列（为等比数列,其中正确的结论是（ ）‎ A、①②③ B、①②④ C、①③④ D、①④‎ ‎ 二、填空题：（每小题5分，共20分）‎ ‎13、的展开式中，的系数为 。‎ ‎14、若,则 。‎ ‎15、椭圆的左焦点为F，直线与椭圆相交于点A、B，当的周长最大时，的面积是 。‎ ‎16、已知是夹角为的单位向量，关于实数x的方程有解，则的取值范围是 。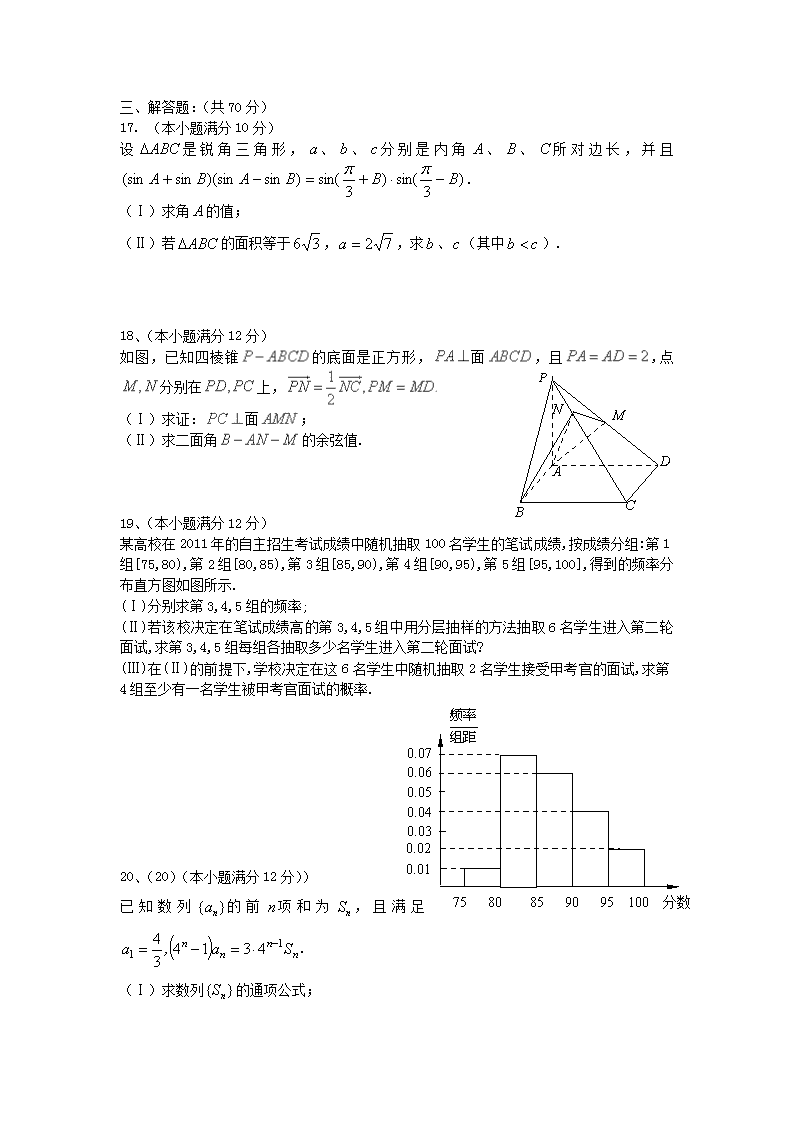‎ 三、解答题：（共70分）‎ ‎17. （本小题满分10分）‎ 设是锐角三角形，、、分别是内角、、所对边长，并且.‎ ‎（Ⅰ）求角的值；‎ ‎（Ⅱ）若的面积等于，，求、（其中）. ‎ ‎18、（本小题满分12分）‎ 如图，已知四棱锥的底面是正方形，面，且,点分别在上，‎ ‎（Ⅰ）求证：面；‎ ‎（Ⅱ）求二面角的余弦值.‎ ‎19、（本小题满分12分）‎ 某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.‎ ‎(Ⅰ)分别求第3,4,5组的频率;‎ ‎(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?‎ ‎(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.‎ ‎ 75 80 85 90 95 100 分数 ‎0.01‎ ‎0.02‎ ‎0.04‎ ‎0.06‎ ‎0.07‎ ‎0.03‎ ‎0.05‎ ‎20、（20）（本小题满分12分））‎ 已知数列的前项和为，且满足.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设求数列的前项和。‎ ‎21、（本小题满分12分）‎ 已知定点A（-3,0），M、N分别为x轴、y轴上的动点（M、N不重合），且,点P在直线MN上，.‎ ‎ （Ⅰ）求动点P的轨迹C的方程；‎ ‎ （Ⅱ）设点Q是曲线上任一点，试探究在轨迹C上是否存在点T，使得点T到点Q的距离最小？若存在，求出该最小距离和点T的坐标，若不存在，说明理由．‎ ‎22、（本小题满分12分）‎ 设函数 ‎ ‎（Ⅰ）若时函数有三个互不相同的零点，求的范围；‎ ‎（Ⅱ）若函数在内没有极值点，求的范围；‎ ‎（Ⅲ）若对任意的，不等式在上恒成立，求实数的取值范围。‎ ‎2014广西高考压轴卷文科数学参考参考 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B D B C A C A B A D C 二、填空题．‎ ‎13．120 14、 15、3 16、‎ 三、解答题：‎ ‎17、解：（Ⅰ），‎ ‎，‎ 即， .‎ 又是锐角三角形，，从而. …………………5分 ‎ ‎（Ⅱ）由（Ⅰ）及已知，得的面积=，①. ‎ 由余弦定理知，，将及代入，得②‎ 由①、②可得.因此是一元二次方程的两个根，解此方程并由知，‎ ‎. …………………10分 ‎18、解：（1）证法1：面，. ‎ ‎ 面 ‎ 面,. 1分 ‎ 是的中点，且， ,面.‎ ‎ 而面，. 3分 点是的三等分点.‎ ‎4分 ‎6分 又且,面. 7分 证法2：，四棱锥的底面是正方形，面，故可以建立如图所示的空间直角坐标系. 又，，，‎ x y z ‎ ，.‎ ‎ ,,3分 设求得. 5分 ‎ ,.‎ 又且, 面.7分 ‎ ‎ ‎（Ⅱ）设平面的法向量为， ‎ ‎ 是平面的法向量， 10分 ‎12分二面角的余弦值. ‎ ‎19、解：解:(Ⅰ)由题意,第组的频率为, ‎ 第组的频率为, ‎ 第组的频率为 ‎ ‎(Ⅱ)第组的人数为, ‎ 第组的人数为, ‎ 第组的人数为. ‎ 因为第,,组共有名学生,所以利用分层抽样的方法在名学生中抽取名学生,每组抽取的人数分别为: ‎ 第组:, ‎ 第组:, ‎ 第组:. ‎ 所以第,,组分别抽取人,人,人 ‎ ‎(Ⅲ)设第组的名学生为,,, ‎ 第组的名学生为,, ‎ 第组的名学生为. ‎ 则从六名学生中抽两名学生有: ‎ ‎ ‎ 共种可能. ‎ 其中第组的名学生为,至少有一名学生入选的有: ‎ ‎ ‎ 共种可能, ‎ 所以第组至少有一名学生被甲考官面试的概率为 ‎ ‎21．解：（Ⅰ）设点M、N的坐标分别为，（）点P的坐标为，‎ 则，，‎ 由得，------------------（※）............2分 由得∴代入（※）得...‎ ‎5分 ∵∴‎ ‎∴动点P的轨迹C的方程为（）...7分 ‎（Ⅱ）曲线即，是以B（4,0）‎ 为圆心，以1为半径的圆,设 T为轨迹C上任意一点，连结TB, ‎ 则∴当最小时，最小..9分 ‎∵点T在轨迹C上，设点（）‎ ‎∴ ......10分 当，即时，有最小值，，当时，‎ ‎∴在轨迹C上存在点T，其坐标为，使得最小，.12分 ‎22. 解：（1）当时，‎ 因为有三个互不相同的零点，所以，‎ 即有三个互不相同的实数根。‎ 令，则。‎ 因为在和均为减函数，在为增函数，‎ 的取值范围 ‎ ‎（2）由题可知，方程在上没有实数根，‎ 因为，所以 ‎（3）∵，且，‎ ‎∴函数的递减区间为，递增区间为和；‎ 当时，又，‎ ‎∴而 ‎∴，‎ 又∵在上恒成立，‎ ‎∴，即，即在恒成立。‎ ‎∵的最小值为 ‎∴‎