山东高考数学答案理科 5页

‎2012年普通高等学校招生全国统一考试（山东卷）‎ 文理数学合卷 ‎ ‎ 注意事项：‎ ‎1. 答题前，考生务必用0.5毫米的签字笔将自己的姓名、座号、准考证号、县区和科类填写在自己的答题卡和试卷规定的位置上。‎ ‎2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。答案不能打在试卷上。‎ ‎3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。不按以上要求最大的答案无效。‎ ‎4. 第Ⅱ卷第六题为选做题，考生须从所给（一）（二）两题中任选一题作答，不能全选。‎ 参考公式：‎ 柱体的体积公式，其中表示柱体的底面积，表示柱体的高 球的体积公式V=πR3 ，其中R是球的半径 球的表面积公式：S=4πR2,其中R是球的半径 用最小二乘法求线性回归方程系数公式 如果事件互斥，那么.[来源:学#科#网Z#X#X#K]‎ 如果事件相互独立，那么 ‎ 第Ⅰ卷(共60分)‎ 一、选择题：本大题共l2小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。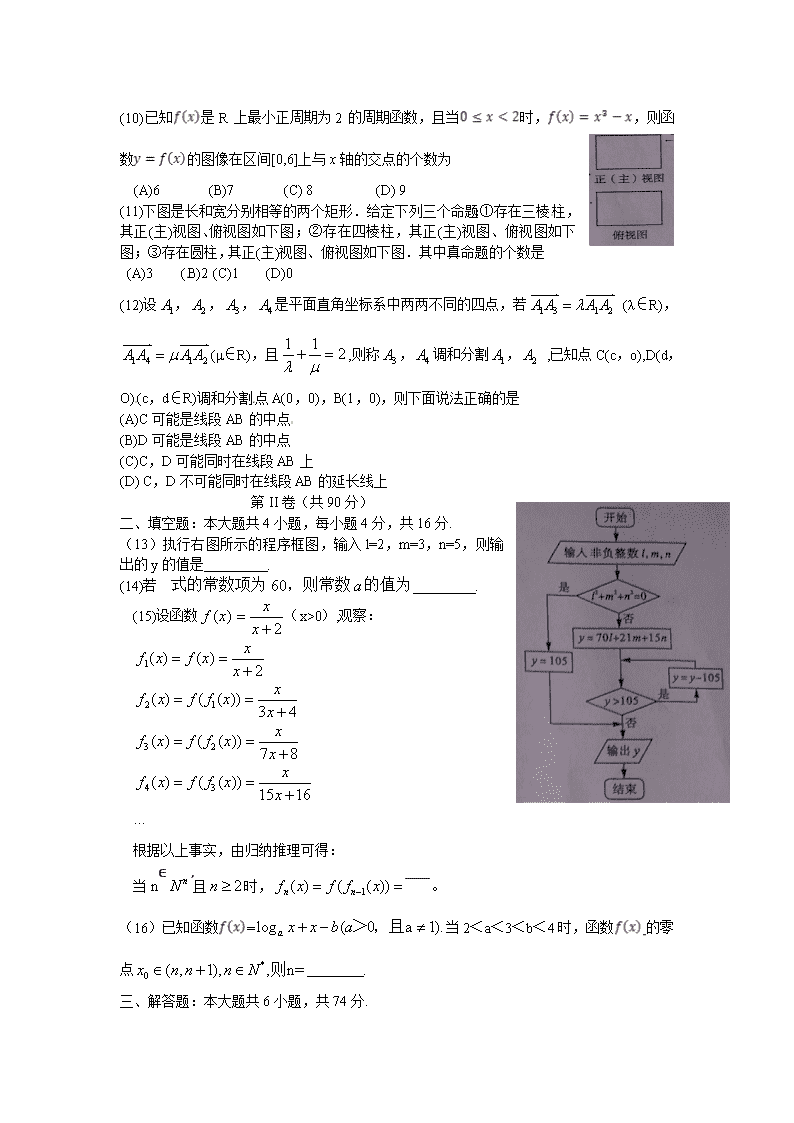‎ ‎(1)设集合 M ={x|}，N ={x|},则M∩N =‎ ‎（A）[1,2) (B)[1,2] (C)( 2,3] (D)[2,3]‎ ‎(2)复数z=(为虚数单位)在复平面内对应的点所在象限为：‎ ‎（A）第一象限 (B)第二象限 (C)第三象限 (D)第四象限 ‎ (6)若函数(ω>0)在区间上单调递增，在区间上单调递减，则ω=‎ ‎ (A) (B) (C)2 (D)3‎ ‎（7）某产品的广告费用x与销售额y的统计数据如下表 根据上表可得回归方程中的为9.4，据此模型预报广告费用为6万元时销售额为 ‎(A)63.6万元 (B)65.5万元 (C)67.7万元 (D)72.0万元 ‎(8)已知双曲线的两条渐近线均和圆C：相切且双曲线的右焦点为圆C的圆心，则该双曲线的方程为 ‎(A) (B) (C) (D) ‎ （9）函数的图象大致是 ‎(10)已知是R上最小正周期为2的周期函数，且当时，，则函数的图像在区间[0,6]上与x轴的交点的个数为 ‎ (A)6 (B)7 (C) 8 (D) 9 ‎ ‎(11)下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是 ‎ (A)3 (B)2 (C)1 (D)0‎ ‎(12)设，，，是平面直角坐标系中两两不同的四点，若 (λ∈R)，(μ∈R)，且,则称，调和分割， ,已知点C(c，o),D(d，O)(c，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是 ‎(A)C可能是线段AB的中点 ‎ ‎(B)D可能是线段AB的中点 ‎(C)C，D可能同时在线段AB上 ‎ ‎(D) C，D不可能同时在线段AB的延长线上 第II卷（共90分）‎ 二、填空题：本大题共4小题，每小题4分，共16分.‎ ‎（13）执行右图所示的程序框图，输入l=2，m=3，n=5，则输出的y的值是 .‎ ‎(14)若 式的常数项为60，则常数的值为 .‎ ‎(15)设函数（x>0）,观察：‎ ‎[来源:Z§xx§k.Com]‎ ‎…‎ 根据以上事实，由归纳推理可得：‎ 当n∈,且时，_____。‎ ‎（16）已知函数=当2＜a＜3＜b＜4时，函数的零点 .‎ 三、解答题：本大题共6小题，共74分. ‎ ‎（19）（本小题满分12分）‎ 在如图所示的几何体中，四边形ABCD为平行四边形，∠ ACB=，EA ⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC，AB=2EF.‎ ‎（I）若M是线段AD上的中点，求证：CM ∥平面ABFE;‎ ‎（II）若AC＝BC=2AE，求平面角ABFC的大小． ‎ ‎（20）（本小题满分12分）‎ 等比数列中，分别是下表第一、二、三行中的某一个数，且中的任何两个数不在下表的同一列.‎ 第一列 第二列[‎ 第三列 第一行 ‎3[来源:学_科_网]‎ ‎2‎ ‎10‎ 第二行 ‎6‎ ‎4‎ ‎14‎ 第三行 ‎9‎ ‎8‎ ‎18‎ ‎（Ⅰ）求数列的通项公式； ‎ ‎（Ⅱ）若数列满足：，求数列的前项和.‎ ‎（21）（本小题满分12分）‎ 某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为立方米，且.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为.设该容器的建造费用为千元.‎ ‎（Ⅰ）写出关于的函数表达式，并求该函数的定义域；‎ ‎（Ⅱ）求该容器的建造费用最小时的. ‎ ‎（22）（本小题满分14分）[来源:学|科|网Z|X|X|K]‎ 已知直线l与椭圆C: 交于两不同点，且△OPQ的面积S=,其中O为坐标原点。‎ ‎（Ⅰ）证明均为定值.‎ ‎（Ⅱ）设线段PQ的中点为M，求|OM|·|PQ|的最大值；‎ ‎（Ⅲ）椭圆C上是否存在点三点D,E,G，使得S△ODE= S△ODG= S△OEG=？ ‎ 若存在，判断△DEG的形状；若不存在，请说明理由。‎