文科数学高考专题复习训练——概率与统计 7页

文科数学高考专题复习训练——概率与统计 ‎1.（本小题满分12分）‎ 城市公交车的数量若太多则容易造成资源的浪费；若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间作为样本分成5组，如下表所示（单位：分钟）：‎ 组别 候车时间 人数 一 ‎ ‎ ‎2‎ 二 ‎6‎ 三 ‎4‎ 四 ‎2‎ 五 ‎1‎ ‎（1）估计这60名乘客中候车时间少于10分钟的人数；‎ ‎（2）若从上表第三、四组的6人中任选2人作进一步的调查，求抽到的两人恰好来自不同组的概率．‎ ‎1.解:（1）候车时间少于10分钟的概率为， ………………4分 所以候车时间少于10分钟的人数为人． ………………………6分 ‎ （2）将第三组乘客编号为，第四组乘客编号为．从6人中任选两人有包 含以下基本事件：，‎ ‎ ，，， ‎ ‎ ， ………………10分 ‎ 其中两人恰好来自不同组包含8个基本事件,所以,所求概率为．………12分 概率与统计2．（本小题共13分）‎ 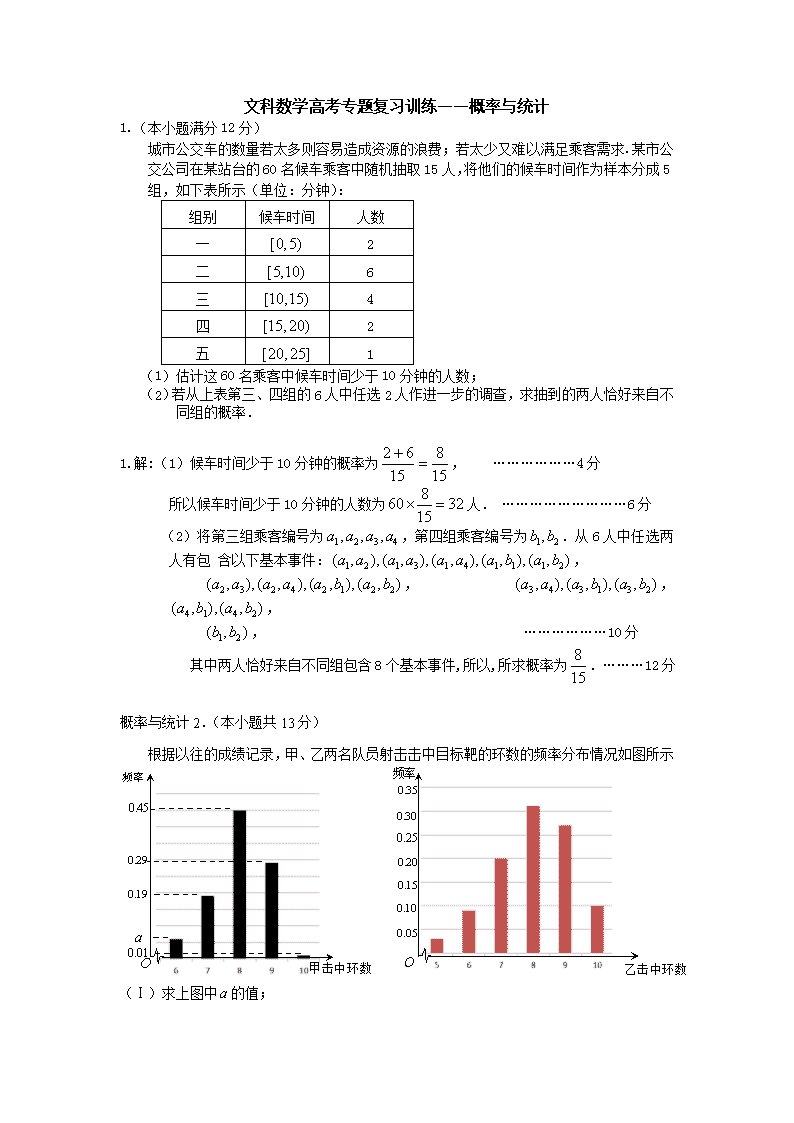根据以往的成绩记录，甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示 ‎（Ⅰ）求上图中的值；‎ ‎（Ⅱ）甲队员进行一次射击，求命中环数大于7环的概率（频率当作概率使用）；‎ ‎（Ⅲ）由上图判断甲、乙两名队员中，哪一名队员的射击成绩更稳定（结论不需证明）.‎ ‎2．解：（Ⅰ）由上图可得, ‎ 所以. ----------------------------------4分 ‎（Ⅱ）设事件A为“甲队员射击，命中环数大于7环”，它包含三个两两互斥的事件：甲队员射击，命中环数为8环，9环，10环.‎ ‎ 所以. ----------------------------------9分 ‎（Ⅲ）甲队员的射击成绩更稳定. ---------------------------------13分 概率与统计3．某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图．‎ ‎（Ⅰ）比较这两名队员在比赛中得分的均值和方差的大小；‎ ‎（Ⅱ）从乙比赛得分在20分以下的6场比赛中随机抽取2场进行失误分析，求抽到恰好有1场得分不足10分的概率．‎ ‎3解　（Ⅰ）甲＝(7＋9＋11＋13＋13＋16＋23＋28)＝15，‎ 乙＝(7＋8＋10＋15＋17＋19＋21＋23)＝15，‎ s＝[(－8)2＋(－6)2＋(－4)2＋(－2)2＋(－2)2＋12＋82＋132]＝44.75，‎ s＝[(－8)2＋(－7)2＋(－5)2＋02＋22＋42＋62＋82]＝32.25.‎ 甲、乙两名队员的得分均值相等；甲的方差比乙的方差大．‎ ‎（Ⅱ）依题意，在20分以下的6场比赛中乙的得分为：7,8,10,15,17,19.‎ 从中随机抽取2场，这2场比赛的得分如下：(7,8)，(7,10)，(7,15)，(7,17)，(7,19)，(8,10)，(8,15)，(8,17)，(8,19)，(10,15)，(10,17)，(10,19)，(15,17)，(15,19)，(17,19)，共15种可能，其中恰好有1场得分在10分以下的情形是：(7,10)，(7,15)，(7,17)，(7,19)，(8,10)，(8,15)，(8,17)，(8,19)，共8种可能．所以，所求概率为P＝.‎ 概率与统计4.‎ 一个袋中装有四个形状大小完全相同的球，球的编号分别为1,2,3,4.‎ ‎（Ⅰ）从袋中随机抽取一个球，将其编号记为a，然后从袋中余下的三个球中再随机抽取一个球，将其编号记为b，求关于x的一元二次方程x2＋2ax＋b2＝0有实根的概率；‎ ‎（Ⅱ）先从袋中随机取一个球，该球的编号记为m，将球放回袋中，然后从袋中随机取一个球，该球的编号记为n.若以(m，n)作为点P的坐标，求点P落在区域内的概率．‎ ‎4解　（Ⅰ）设事件A为“方程x2＋2ax＋b2＝0有实根”．‎ 当a>0，b>0时，方程x2＋2ax＋b2＝0有实根的充要条件为a≥b.‎ 以下第一个数表示a的取值，第二个数表示b的取值．‎ 基本事件共12个：(1,2)，(1,3)，(1,4)，(2,1)，(2,3)，(2,4)，(3,1)，(3,2)，(3,4)，(4,1)，(4,2)，(4,3)．‎ 事件A中包含6个基本事件：(2,1)，(3,1)，(3,2)，(4,1)，(4,2)，(4,3)．‎ 事件A发生的概率为P(A)＝＝.‎ ‎（Ⅱ）先从袋中随机取一个球，放回后再从袋中随机取一个球，点P(m，n)的所有可能情况为：(1,1)，(1,2)，(1,3)，(1,4)，(2,1)，(2,2)，(2,3)，(2,4)，(3,1)，(3,2)，(3,3)，(3,4)，(4,1)，(4,2)，(4,3)，(4,4)，共16个．‎ 落在区域内的有(1,1)，(2,1)，(2,2)，(3,1)，共4个，‎ 所以点P落在区域内的概率为.‎ 概率与统计5.‎ 经销商经销某种农产品，在一个销售季度内，每售出1 t该产品获利润500元，未售出的产品，每1 t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图如图所示．经销商为下一个销售季度购进了130 t该农产品．以X(单位：t,100≤X≤150)表示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季度内经销该农产品的利润．‎ ‎(1)将T表示为X的函数；‎ ‎(2)根据直方图估计利润T不少于57 000元的概率．‎ ‎5解：(1)当X∈[100,130)时，‎ T＝500X－300(130－X)＝800X－39 000.‎ 当X∈[130,150]时，‎ T＝500×130＝65 000.‎ 所以T＝ ‎(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.‎ 由直方图知需求量X∈[120,150]的频率为0.7，所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.‎ 概率与统计6.‎ 某市拟举行一项庆典活动．新闻媒体对此进行了网上调查，所有参与调查的人中，持“支持”“保留”和“不支持”态度的人数如下表所示：‎ 支持 保留 不支持 ‎20岁以下 ‎800‎ ‎450‎ ‎200‎ ‎20岁以上(含20岁)‎ ‎100‎ ‎150‎ ‎300‎ ‎(1)在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持”态度的人中抽取了45人，求n的值；‎ ‎(2)在持“不支持”态度的人中，用分层抽样的方法抽取5人看作一个总体，从这5人中任意选取2人，求至少有1人在20岁以下的概率．‎ ‎6．解：(1)由题意得＝，解得n＝100.‎ ‎(2)设所选取的人中，有m人20岁以下，则＝，解得m＝2.‎ 即从20岁以下抽取2人，另一部分抽取3人，分别记作A1，A2；B1，B2，B3，‎ 则从中任取2人的所有基本事件为(A1，B1)，(A1，B2)，(A1，B3)，(A2，B1)，(A2，B2)，(A2，B3)，(A1，A2)，(B1，B2)，(B2，B3)，(B1，B3)，共10个．‎ 其中至少有1人20岁以下的基本事件有7个：(A1，B1)，(A1，B2)，(A1，B3)，(A2，B1)，(A2，B2)，(A2，B3)，(A1，A2)，‎ 所以从中任意选取2人，至少有1人20岁以下的概率为.‎ 概率与统计7．（本小题满分12分）‎ 某国际会议在北京召开，为了搞好对外宣传工作，会务组选聘了16名男记者和14名女记者担任对外翻译工作，调查发现，男、女记者中分别有10人和6人会俄语．‎ ‎（Ⅰ）根据以上数据完成以下2×2列联表：‎ 会俄语 不会俄语 总计 男 女 总计 ‎30‎ 并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关？‎ 参考公式：K2＝，其中n＝a＋b＋c＋d 参考数据：‎ P(K2≥k0)‎ ‎0.40‎ ‎0.25‎ ‎0.10‎ ‎0.010‎ k0‎ ‎0.708‎ ‎1.323‎ ‎2.706‎ ‎6.635‎ ‎（Ⅱ）会俄语的6名女记者中有4人曾在俄罗斯工作过，若从会俄语的6名女记者中随机抽取2人做同声翻译，求抽出的2人都在俄罗斯工作过的概率．‎ ‎7．解：（Ⅰ）由已知，得2×2列联表：‎ 会俄语 不会俄语 总计 男 ‎10‎ ‎6‎ ‎16‎ 女 ‎6‎ ‎8‎ ‎14‎ 总计 ‎16‎ ‎14‎ ‎30‎ 假设是否会俄语与性别无关．由已知数据，可得 K2＝≈1.1575＜2.706，‎ 所以在犯错的概率不超过0.10的前提下不能判断会俄语与性别有关．‎ ‎（Ⅱ）会俄语的6名女记者分别为A，B，C，D，E，F，其中A，B，C，D曾在俄罗斯工作过．从这6人任取2人有（A，B），（A，C），（A，D），（A，E），（A，F），（B，C），（B，D），（B，E），（B，F），（C，D），（C，E），（C，F），（D，E），（D，F），（E，F）共15种，其中2人都在俄罗斯工作过的是（A，B），（A，C），（A，D），（B，C），（B，D），（C，D）共6种，所以抽出的女记者中，2人都在俄罗斯工作过的概率是P＝＝．‎ 概率与统计8.选择填空 ‎1．抛掷甲、乙两枚质地均匀且四面上分别标有1,2,3,4的正四面体，其底面落于桌面，记所得的数字分别为x，y，则为整数的概率是________．‎ ‎2.在区域D：内随机取一个点，则此点到点A(1，2)的距离大于2的概率是（ ）‎ A. B. C. D. ‎ ‎3.从长度分别为1、2、3、4的四条线段中任意取三条，则以这三条线段为边可以构成三角形的概率是 ．‎ ‎4已知，若向区域内随机投一点，则点落在区域内的概率为(　　　)‎ A. B. C. D. ‎5在区间上随机地取一个数x,若x满足的概率为,则__________. ‎ ‎1解析：将抛掷甲、乙两枚质地均匀的正四面体所得的数字x，y记作有序实数对(x，y)，共包含16个基本事件，其中为整数的有：(1,1)，(2,2)，(3,3)，(4,4)，(2,1)，(3,1)，(4,1)，(4,2)，共8个基本事件，故所求的概率为＝.答案： ‎2．答案：A ‎3. 1/4‎ ‎4．‎ ‎5【答案】‎ 本题考查绝对值不等式以及几何概型的计算。由题意知，则由得，所以足的概率为，解得。‎