- 783.50 KB
- 2021-05-14 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
高考复习专题:平面向量
第一节 平面向量的概念及其线性运算
向量专题复习
1.向量的有关概念:
(1)向量的定义:既有大小又有方向的量。向量可以任意平移。
(2)零向量:长度为0的向量叫零向量,记作:.
(3)单位向量:长度为一个单位长度的向量叫做单位向量。
任意向量的单位化:与共线的单位向量是.
(4)相等向量:长度相等且方向相同的两个向量叫相等向量。
(5)平行向量又叫共线向量,记作:∥.
①向量与共线,则有且仅有唯一一个实数,使;
②规定:零向量和任何向量平行;
③两个向量平行包含两个向量共线,但两条直线平行不包含两条直线重合;
④相等向量一定是共线向量,但共线向量不一定相等;
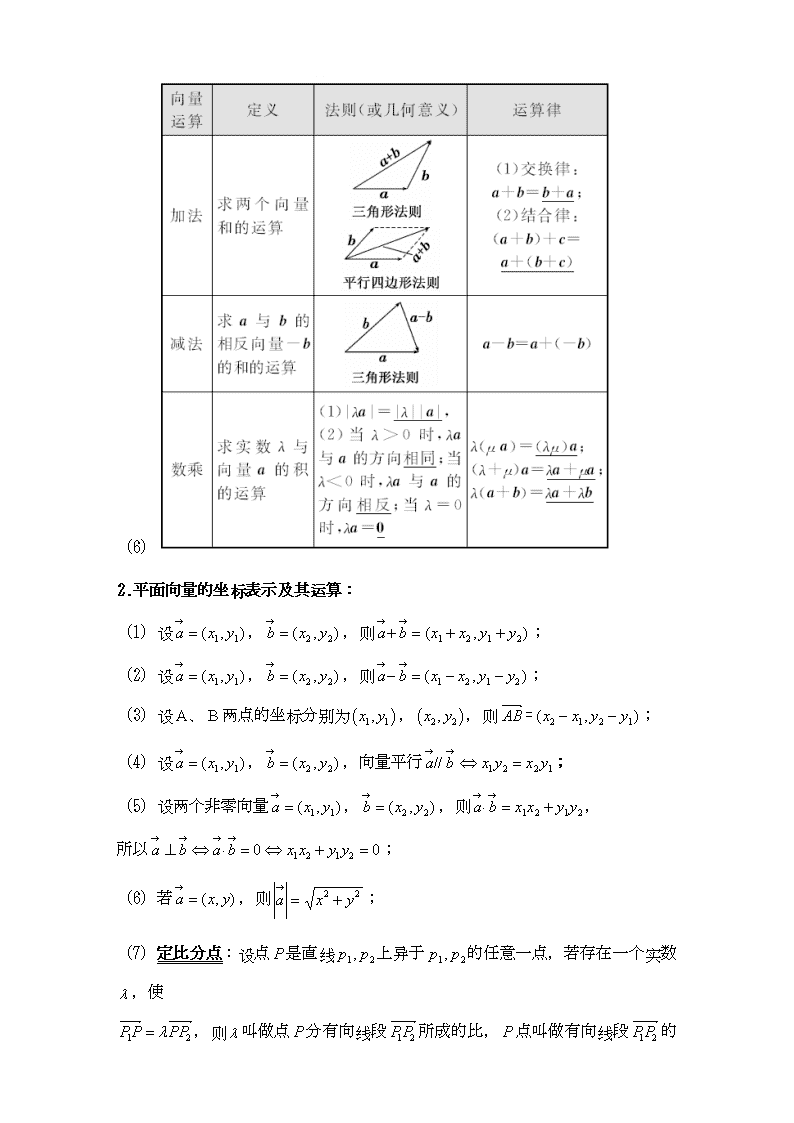
(6)向量的加法和减法满足平行四边形法则或三角形法则;
(6)
2.平面向量的坐标表示及其运算:
(1)设,,则;
(2)设,,则;
(3)设、两点的坐标分别为,,则=;
(4)设,,向量平行;
(5)设两个非零向量,,则,
所以;
(6)若,则;
(7)定比分点:设点是直线上异于的任意一点,若存在一个实数,使
,则叫做点分有向线段所成的比,点叫做有向线段的以定比为的定比分点;当分有向线段所成的比为,则点分有向线段所成的比为.
注意:①设、,分有向线段所成的比为,则,
在使用定比分点的坐标公式时,应明确,、的意义,即分别为分点,起点,终点的坐标。在具体计算时应根据题设条件,灵活地确定起点,分点和终点,并根据这些点确定对应的定比.当时,就得到线段的中点公式.
②的符号与分点的位置之间的关系:
当点在线段上时;
当点在线段的延长线上时 ;
当点在线段的反向延长线上时;
3.平面向量的数量积:
(1)两个向量的夹角:对于非零向量、,作,,称为向量、的夹角。
(2)平面向量的数量积:如果两个非零向量、,它们的夹角为,我们把数量叫做与的数量积(或内积或点积),记作:,即
.
零向量与任一向量的数量积是0,注意:向量的数量积是一个实数,不再是一个向量。
(3)在上的投影为,投影是一个实数,不一定大于0.
(4)的几何意义:数量积等于与在上的投影的乘积。
(5)向量数量积的应用:设两个非零向量、,其夹角为,则,
当时,为直角;
当时,为锐角或同向;
当时,为钝角或反向;
(6)向量三角不等式:
当同向,;
当反向,;
当不共线;
4.平面向量的分解定理
(1)平面向量分解定理:如果、是同一平面内的两个不共线向量,那么对于这一平面内的任意向量,有且只有一对实数、,使成立,我们把不共线的向量、叫做这一平面内所有向量的一组基底。
(2)O为平面任意一点,A、B、C为平面另外三点,则A、B、C三点共线且.
5.空间向量
空间向量是由平面向量拓展而来的,它是三维空间里具有大小和方向的量,它的坐标表示有x,y,z.空间向量的性质与平面向量的性质相同或相似,故在学习空间向量时,可进行类比学习。
如,若、、三个向量共面,则.同时,对于空间任意一点O,存在,其中=____1_________
考点一:向量的概念
[例1] 给出下列四个命题:
①若|a|=|b|,则a=b或a=-b; ②若,则四边形ABCD为平行四边形;
③若a与b同向,且|a|>|b|,则a>b;④λ,μ为实数,若λa=μb,则a与b
共线.
其中假命题的个数为( ) A.1 B.2 C.3 D.4
[答案] D
.
下列说法中错误的是( )
A.有向线段可以表示向量但不是向量,且向量也不是有向线段
B.若向量a和b不共线,则a和b都是非零向量
C.长度相等但方向相反的两个向量不一定共线
D.方向相反的两个非零向量必不相等 [答案] C
[例2] (1)(2014·金华模拟)已知两个非零向量a,b满足|a+b|=|a-b|,则下面结论正确的是( )
A.a∥b B.a⊥b C.|a|=|b| D.a+b=a-b
(2)(2013·四川高考)
如图在平行四边形ABCD中,对角线AC与BD交于点O,则λ= ________.
(3)(2013·江苏高考)设D,E分别是△ABC的边AB,BC上的点,AD=AB,BE=BC.若 (λ1,λ2为实数),则λ1+λ2
的值为________.
[答案] (1)B (2)2 (3)
1.在平行四边形ABCD中,AC与BD相交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若 ( )
A.a+b B.a+b C.a+b D.a+b
易误警示(四)平面向量线性运算中的易误点
[典例] (2013·广东高考)设a是已知的平面向量且a≠0.关于向量a的分解,有如下四个命题:①给定向量b,总存在向量c,使a=b+c;
②给定向量b和c,总存在实数λ和μ,使a=λb+μ c;
③给定单位向量b和正数μ,总存在单位向量c和实数λ,使a=λb+μc;
④给定正数λ和μ,总存在单位向量b和单位向量c,使a=λb+μc.
上述命题中的向量b,c和a在同一平面内且两两不共线,则真命题的个数是( )
A.1 B.2 C.3 D.4
[答案] B
下列命题中正确的是( )
A.向量a,b共线的充要条件是有且仅有一个实数λ,使b=λa
B.在△ABC中,
C.不等式||a|-|a+b||≤|a+b|≤|a|+|b|中两个等号不可能同时成立
D.向量a,b不共线,则向量a+b与向量a-b必不共线
第二节 平面向量基本定理及坐标表示
1.两个向量的夹角
(1) 定义:
已知两个非零向量a和b,作则∠AOB=θ叫做向量a与b的夹角.
(2)范围:向量夹角θ的范围是[0,π],a与b同向时,夹角θ=0;a与b反向时,夹角θ=π.
(3)向量垂直:如果向量a与b的夹角是,则a与b垂直,记作a⊥b.
2.平面向量基本定理及坐标表示
(1)平面向量基本定理:如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2
.其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组基底.
(2)平面向量的坐标表示:
①在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i,j作为基底.对于平面内的一个向量a,由平面向量基本定理可知,有且只有一对实数x,y,使得a=xi+yj,这样,平面内的任一向量a都可由x,y唯一确定,我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y),其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.
3.平面向量的坐标运算
(1)若a=(x1,y1),b=(x2,y2),则a±b=(x1±x2,y1±y2);
(2)若A(x1,y1),B(x2,y2),则 (x2-x1,y2-y1);
(3)若a=(x,y),则λa=(λx,λy);
(4)若a=(x1,y1),b=(x2,y2),则a∥b⇔x1y2=x2y1.
[例1] 在平行四边形ABCD中,E和F分别是边CD和BC的中点.若其中λ,μ∈R,则λ+μ=________. [答案]
:在本例条件下,若试用c,d表示
:如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点.若则λ+μ=________.
答案:
1.(2014·福建高考)在下列向量组中,可以把向量a=(3,2)表示出来的是( )
A.e1=(0,0),e2=(1,2) B.e1=(-1,2),e2=(5,-2)
C.e1=(3,5),e2=(6,10) D.e1=(2,-3),e2=(-2,3)
解析:选B
[例3] (1)(2013·陕西高考)已知向量a=(1,m),b=(m,2),若a∥b,则实数m等于( )
A.- B. C.-或 D.0
(2)(2014·丽水模拟)设向量a,b满足|a|=2,b=(2,1),且a与b的方向相反,则a的坐标为________.
(3)(2014·台州模拟)若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则+的值等于________.
[答案] (1)C (2)(-4,-2) (3)
1.(2013·辽宁高考)已知点A(1,3),B(4,-1),则与向量AB―→同方向的单位向量为( )
A. B. C. D.
2.已知向量a=(m,-1),b=(-1,-2),c=(-1,2),若(a+b)∥c,则m=________.
答案:
3.已知点A(4,0),B(4,4),C(2,6),则AC与OB的交点P的坐标为________.
答案:(3,3)
易误警示(五)平面向量坐标运算中的易误点
用平面向量解决相关问题时,在便于建立平面直角坐标系的情况下建立平面直角坐标系,可以使向量的坐标运算更简便一些.
[典例] (2013·北京高考)向量a,b,c在正方形网格中的位置如图所示.若c=λa+μb(λ,μ∈R),则=________.
[答案] 4
答案:2
第三节 平面向量的数量积及平面向量的应用
1.平面向量数量积的定义:已知两个非零向量a和b,它们的夹角为θ,把数量|a||b|cos θ 叫做a和b的数量积(或内积),记作a·b.即a·b=|a||b|cos θ,规定0·a=0.
2.向量数量积的运算律
(1)a·b=b·a;(2)(λa)·b=λ(a·b)=a·(λb);(3)(a+b)·c=a·c+b·c.
3.平面向量数量积的有关结论
已知非零向量a=(x1,y1),b=(x2,y2),
结论
几何表示
坐标表示
模
|a|=
|a|=
夹角
cos θ=
cos θ=
a⊥b的充
要条件
a·b=0
x1x2+y1y2=0
[例1] (1)(2014·天津高考)已知菱形ABCD的边长为2,∠BAD=120°,点E,F 分别在边BC,DC上,BC=3BE,DC=λDF.若则 λ的值为________.
(2)如图,在矩形ABCD中,AB=,BC=2,点E为BC的中点,点F在边CD上,若
、
[答案] (1)2 (2)
:在本例(2)中,若四边形ABCD是边长为1的正方形,点E是AB上的动点,求的值及的最大值.
答案:1.
1.若向量a=(1,1),b=(2,5),c=(3,x),满足条件(8a-b)·c=30,则x=________.
答案:4
2.已知e1,e2是夹角为的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则实数k的值为________.
答案:
[例2] (1)(2014·湖南高考)在平面直角坐标系中,O 为原点,A(-1,0),B(0,),C(3,0),动点D满足 ( )
A. [4,6] B.[-1,+1]
C.[2,2] D.[-1,+1]
(2)(2014·四川高考)平面向量a=(1,2),b=(4,2),c=ma+b(m∈R),且c与a的夹角等于c与b的夹角,则m=________.
[答案] (1)D (2)2
1.若a=(1,2),b=(1,-1),则2a+b与a-b的夹角等于( )
A.- B. C. D.π
解析:选C
2.已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k=________.
答案:1
3.已知平面向量α,β,|α|=1,β=(2,0),α⊥(α-2β),则|2α+β|的值为________.
答案:
[例3] (1)(2014·浙江高考)设θ为两个非零向量a,b的夹角.已知对任意实数t,|b+ta|的最小值为1.( )
A.若θ确定,则|a|唯一确定 B.若θ确定,则|b|唯一确定
C.若|a|确定,则θ唯一确定 D.若|b|确定,则θ唯一确定
[答案] (1)B