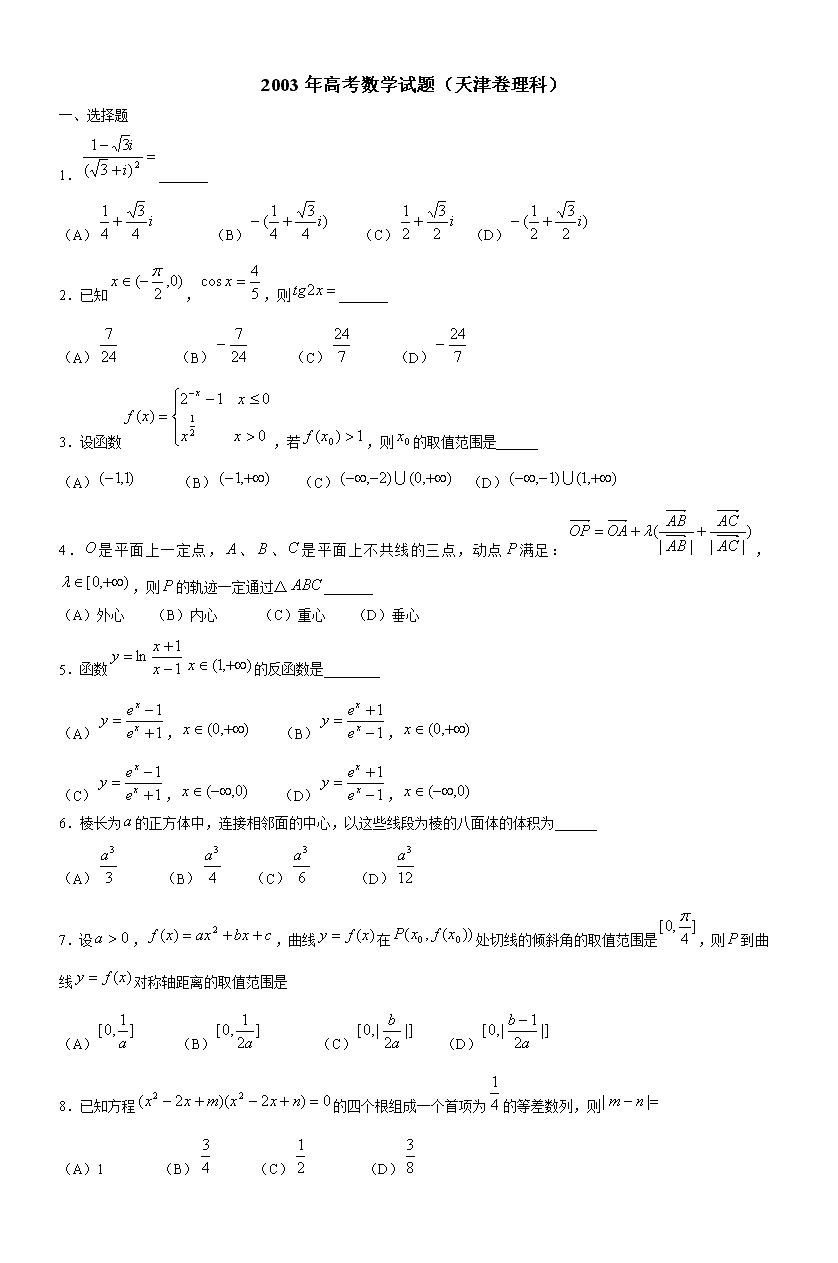高考数学试题天津卷理科 4页

‎2003年高考数学试题（天津卷理科）‎ 一、选择题 ‎1．_______‎ ‎（A）　　　　（B）　　（C）　（D）‎ ‎2．已知，，则_______‎ ‎（A）　　　　（B）　　　（C）　　　（D）‎ ‎3．设函数，若，则的取值范围是______‎ ‎（A）　　　（B）　　（C）　（D）‎ ‎4．是平面上一定点，、、是平面上不共线的三点，动点满足：，，则的轨迹一定通过△_______‎ ‎（A）外心　　（B）内心　　　（C）重心　　（D）垂心 ‎5．函数的反函数是________‎ ‎（A），　　（B），‎ ‎（C），　　（D），‎ ‎6．棱长为的正方体中，连接相邻面的中心，以这些线段为棱的八面体的体积为______‎ ‎（A）　　　（B）　　（C）　　　（D）‎ ‎7．设，，曲线在处切线的倾斜角的取值范围是，则到曲线对称轴距离的取值范围是 ‎（A）　　　（B）　　　　（C）　　（D）‎ ‎8．已知方程的四个根组成一个首项为的等差数列，则 ‎（A）1　　　　（B）　　　（C）　　　　（D）‎ ‎9．已知双曲线中心在原点且一个焦点，直线与其相交于两点，的中点的横坐标为，则此以曲线的方程是 ‎（A）　　（B）　　（C）（D）‎ ‎10．已知长方形的四个顶点，，和，一质点从的中点沿与夹角为的方向射到上的后，依次反射到和上的和（入射角等于反射角），设的坐标为，若，则的取值范围是 ‎（A）　　　　（B）　　　（C）　　　（D）‎ ‎11．＝‎ ‎（A）3　　　　（B）　　　　（C）　　　　（D）6‎ ‎12．一个四面体的所有棱长都为，四个顶点在同一球面上，则此球的表面积为 ‎（A）　　（B）　　　（C）　　　（D）‎ 二、填空题 ‎13．展开式中的系数是 ‎ ‎14．某公司生产三种型号的轿车，产量分别为1200辆、6000辆、2000辆。为检验该公司的产品的质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取　　　　　、　　　　、　　　　　辆 ‎15．某城市在中心广场建造一个花圃，花圃分为6个部分（如图），现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有　　种（以数字作答）‎ ‎16．下列五个正方体图形中，是正方体的一条对角线，点分别为其所在棱的中点。能得出面的图形的序号是　　　　　（写出所有符合要求的图形序号）‎ 三、解答题 ‎17．已知函数 ‎（1）求函数的最小正周期和最大值；‎ ‎（2）在给出的直角坐标系中，画出在区间上的图象 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18．如图，在直三棱柱中，底面是等腰直角三角形，，侧棱，分别是与的中点，点在平面上的射影是△的重心．‎ ‎（1）求与平面所成角的大小（结果用反三角函数值表示）；‎ ‎（2）求点到平面的距离．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎19．设，求函数，的单调区间.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎20．、两个代表队进行乒乓球对抗赛，每队三名队员，队队员是，队队员是，按以往多次比赛的统计，对阵队员之间胜负概率如下：‎ 对阵队员 A队队员胜的概率 B队队员胜的概率 A1对B1‎ A2对B2‎ A3对B3‎ 现按表中对阵方式出场，每场胜队得1分，负队得0分，设队，队最后所得部分分别为，。‎ ‎（1）求，的概率分布； （2）求，‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎21．已知常数，向量，。经过原点以为方向向量的直线与经过定点以为方向向量的直线相交于点，其中。‎ 试问：是否存在两个定点使得为定值。若存在，求出的坐标，若不存在，说明理由。‎ ‎22．设为常数，且（）‎ ‎（1）证明对任意，；‎ ‎（2）假设对任意有，求的取值范围。‎