高考物理弹簧模型总结 7页

特级教师分析2013年高考物理必考题：含弹簧的物理模型 ‎【命题规律】 ‎ 高考中常出现的物理模型中，斜面问题、叠加体模型、含弹簧的连接体、传送带模型等在高考中的地位特别重要，本专题就这几类模型进行归纳总结和强化训练；传送带问题在高考中出现的概率也较大，而且解题思路独特，本专题也略加论述．‎ 有些问题在高考中变化较大，或者在前面专题中已有较全面的论述，在这里就不再论述和例举．试卷中下列常见的物理模型出现的概率较大：斜面问题、叠加体模型(包含子弹射入)、带电粒子的加速与偏转、天体问题(圆周运动)、轻绳(轻杆)连接体模型、传送带问题、含弹簧的连接体模型．‎ 高考命题以《考试大纲》为依据，考查学生对高中物理知识的掌握情况，体现了“知识与技能、过程与方法并重”的高中物理学习思想．每年各地的高考题为了避免雷同而千变万化、多姿多彩，但又总有一些共性，这些共性可粗略地总结如下：‎ 三、含弹簧的物理模型 纵观历年的高考试题，和弹簧有关的物理试题占有相当大的比重．高考命题者常以弹簧为载体设计出各类试题，这类试题涉及静力学问题、动力学问题、动量守恒和能量守恒问题、振动问题、功能问题等，几乎贯穿了整个力学的知识体系．为了帮助同学们掌握这类试题的分析方法，现将有关弹簧问题分类进行剖析．‎ 对于弹簧，从受力角度看，弹簧上的弹力是变力；从能量角度看，弹簧是个储能元件．因此，弹簧问题能很好地考查学生的综合分析能力，故备受高考命题老师的青睐． ‎ ‎“高考直通车”联合衡水毕业清华北大在校生将于2013年5月中旬推出的手写版高考复习笔记，希望对大家复习备考有所帮助。该笔记适合2014年、2015年、2016年高考生使用。凡2013年5月中旬之后购买的高一、高二同学，每年指定日期可以免费更换一次最新一年的笔记。另外，所有笔记使用者将被加入2014年高考备考专用平台，每周定期提供最新资料和高考互动。笔记对外公开时间：5月20日 ‎ ‎1．静力学中的弹簧问题 ‎(1)胡克定律：F＝kx，ΔF＝k·Δx．‎ ‎(2)对弹簧秤的两端施加(沿轴线方向)大小不同的拉力，弹簧秤的示数一定等于挂钩上的拉力．‎ ‎●例4　如图9－12甲所示，两木块A、B的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，两弹簧分别连接A、B，整个系统处于平衡状态．现缓慢向上提木块A，直到下面的弹簧对地面的压力恰好为零，在此过程中A和B的重力势能共增加了(　　)‎ ‎【解析】取A、B 以及它们之间的弹簧组成的整体为研究对象，则当下面的弹簧对地面的压力为零时，向上提A的力F恰好为：‎ F＝(m1＋m2)g 设这一过程中上面和下面的弹簧分别伸长x1、x2，如图9－12乙所示，由胡克定律得：‎ 故A、B增加的重力势能共为：‎ ‎．‎ ‎[答案]　D ‎【点评】①计算上面弹簧的伸长量时，较多同学会先计算原来的压缩量，然后计算后来的伸长量，再将两者相加，但不如上面解析中直接运用Δx＝ΔF/k进行计算更快捷方便．‎ ‎②通过比较可知，重力势能的增加并不等于向上提的力所做的功．‎ ‎2．动力学中的弹簧问题 ‎(1)瞬时加速度问题(与轻绳、轻杆不同)：一端固定、 另一端接有物体的弹簧，形变不会发生突变，弹力也不会发生突变．‎ ‎(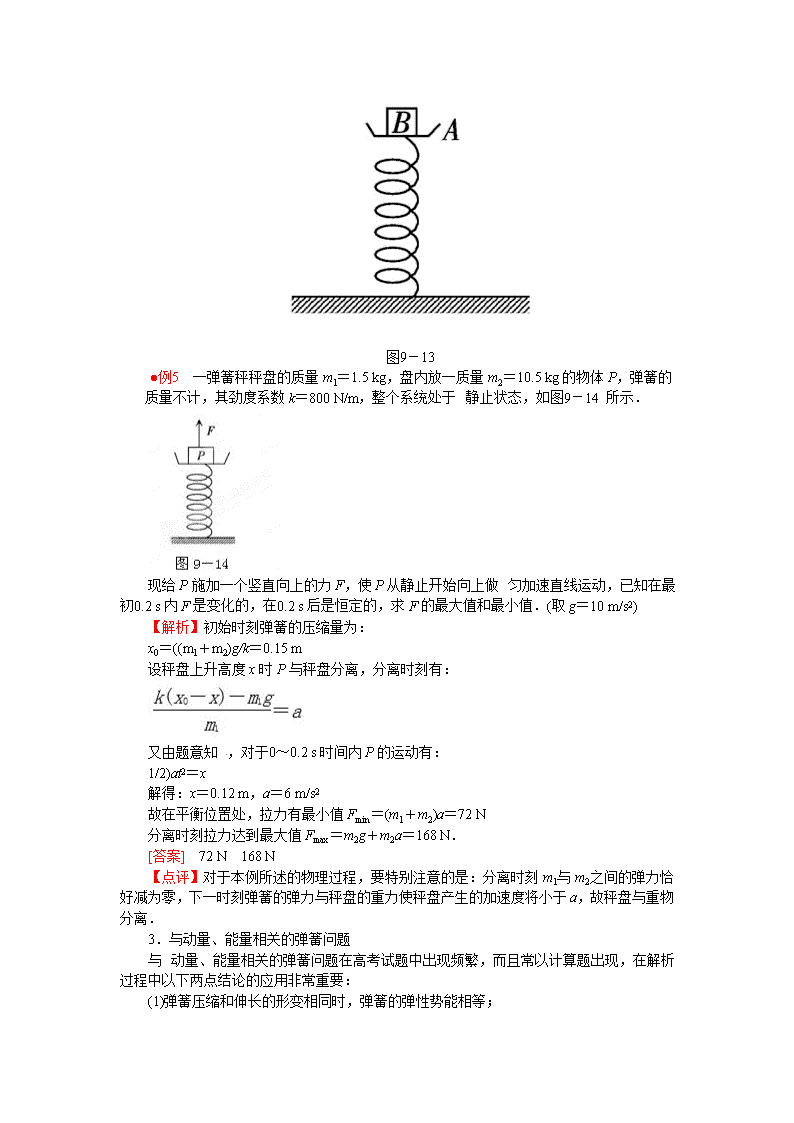2)如图9－13所示，将A、B下压后撤去外力，弹簧在恢复原长时刻B与A开始分离．‎ ‎ ‎ 图9－13‎ ‎●例5　一弹簧秤秤盘的质量m1＝1.5 kg，盘内放一质量m2＝10.5 kg的物体P，弹簧的质量不计，其劲度系数k＝800 N/m，整个系统处于 静止状态，如图9－14 所示．‎ 现给P施加一个竖直向上的力F，使P从静止开始向上做 匀加速直线运动，已知在最初0.2 s内F是变化的，在0.2 s后是恒定的，求F的最大值和最小值．(取g＝10 m/s2)‎ ‎【解析】初始时刻弹簧的压缩量为：‎ x0＝((m1＋m2)g/k＝0.15 m 设秤盘上升高度x时P与秤盘分离，分离时刻有：‎ 又由题意知 ，对于0～0.2 s时间内P的运动有：‎ ‎1/2)at2＝x 解得：x＝0.12 m，a＝6 m/s2‎ 故在平衡位置处，拉力有最小值Fmin＝(m1＋m2)a＝72 N 分离时刻拉力达到最大值Fmax＝m2g＋m2a＝168 N．‎ ‎[答案]　72 N　168 N ‎【点评】对于本例所述的物理过程，要特别注意的是：分离时刻m1与m2之间的弹力恰好减为零，下一时刻弹簧的弹力与秤盘的重力使秤盘产生的加速度将小于a，故秤盘与重物分离．‎ ‎3．与动量、能量相关的弹簧问题 与 动量、能量相关的弹簧问题在高考试题中出现频繁，而且常以计算题出现，在解析过程中以下两点结论的应用非常重要：‎ ‎(1)弹簧压缩和伸长的形变相同时，弹簧的弹性势能相等；‎ ‎(2)弹簧连接两个物体做变速运动时，弹簧处于原长时两物体的相对速度最大，弹簧的形变最大时两物体的速度相等．‎ ‎●例6　如图9－15所示，用轻弹簧将质量均为m＝1 kg的物块A和B连接起来，将它们固定在空中，弹簧处于原长状态，A距地面的高度h1＝0.90 m．同时释放两物块，A与地面碰撞后速度立即变为零，由于B压缩弹簧后被反弹，使A刚好能离开地面(但不继续上升)．若将B物块换为质量为2m的物块C(图中未画出)，仍将它与A固定在空中且弹簧处于原长，从A距地面的高度为h2处同时释放，C压缩弹簧被反弹后，A也刚好能离开地面．已知弹簧的劲度系数k＝100 N/m，求h2的大小．‎ ‎【解析】设A物块落地时，B物块的速度为v1，则有：‎ 设A刚好离地时，弹簧的形变量为x，对A物块有：‎ mg＝kx 从A落地后到A刚好离开地面的过程中，对于A、B及弹簧组成的系统机械能守恒，则有：‎ ‎1/2·mv12＝mgx＋ΔEp 换成C后，设A落地时，C的速度为v2，则有：‎ ‎1/2·2mv22＝2mgh2‎ 从A落地后到A刚好离开地面的过程中，A、C及弹簧组成的系统机械能守恒，则有：‎ 联立解得：h2＝0.5 m．‎ ‎[答案]　0.5 m ‎【点评】由于高中物理对弹性势能的表达式不作要求，所以在高考中几次考查弹簧问题时都要用到上述结论“①”． ‎ ‎●例7　用轻弹簧相连的质量均为2 kg的A、B两物块都以v＝6 m/s的速度在光滑的水平地面上运动，弹簧处于原长，质量为4 kg的物块C静止在前方，如图9－16 甲所示．B与C碰撞后二者粘在一起运动，则在以后的运动中：‎ ‎ ‎ ‎(1)当弹簧的弹性势能最大时，物体A的速度为多大？‎ ‎(2)弹簧弹性势能的最大值是多少？‎ ‎(3)A的速度方向有可能向左吗？为什么？‎ ‎【解析】(1)当A、B、C三者的速度相等(设为vA′)时弹簧的弹性势能最大，由于A、B、C三者组成的系统动量守恒，则有：‎ ‎(mA＋mB)v＝(mA＋mB＋mC)vA′‎ 解得：．‎ ‎(2)B、C发生碰撞时，B、C组成的系统动量守恒，设碰后瞬间B、C两者的速度为v′，则有：‎ mBv＝(mB＋mC)v′‎ 解得：v′＝‎ A的速度为vA′时弹簧的弹性势能最大，设其值为Ep，根据能量守恒 定律得：‎ ‎．‎ ‎(3)方法一　A不可能向左运动．‎ 根据系统动量守恒有：(mA＋mB)v＝mAvA＋(mB＋mC)vB 设A向左，则vA＜0，vB＞4 m/s 则B、C发生碰撞后，A、B、C三者的动能之和为：‎ 实际上系统的机械能为：‎ 根据能量守恒定律可知，E′＞E是不可能的，所以A不可能向左运动．‎ 方法二　B、C碰撞后系统的运动可以看做整体向右匀速运动与A、B和C相对振动的合成(即相当于在匀速运动的车厢中两物块相对振动)‎ 由(1)知整体匀速运动的速度v0＝vA′＝3 m/s 取以v0＝3 m/s匀速运动的物体为参考系，可知弹簧处于原长时，A、B和C相对振动的速率最大，分别为：‎ vAO＝v－v0＝3 m/s vBO＝|v′－v0|＝1 m/s 由此可画出A、B、C的速度随时间变化的图象如图9－16乙所示，故A不可能有向左运动的时刻．‎ ‎[答案]　(1)3 m/s　(2)12 J　(3)不可能，理由略 ‎【点评】①要清晰地想象、理解研究对象的运动过程：相当于在以3 m/s匀速行驶的车厢内，A、B和C做相对弹簧上某点的简谐振动，振动的最大速率分别为3 m/s、1 m/s．‎ ‎②当弹簧由压缩恢复至原长时，A最有可能向左运动，但此时A的速度为零．‎ ‎●例8　探究某种笔的弹跳问题时，把笔分为轻质弹簧、内芯和外壳三部分，其中内芯和外壳质量分别为m和4m．笔的弹跳过程分为三个阶段：‎ ‎①把笔竖直倒立于水平硬桌面，下压外壳使其下端接触桌面(如图9－17甲所示)；‎ ‎②由静止释放，外壳竖直上升到下端距桌面高度为h1时，与静止的内芯碰撞(如图9－17乙所示)；‎ ‎③碰后，内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度为h2处(如图9－17丙所示)．‎ 设内芯与外壳的撞击力远大于笔所受重力，不计摩擦与空气阻力，重力加速度为g．求：‎ ‎(1)外壳与内芯碰撞 后瞬间的共同速度大小．‎ ‎(2)从外壳离开桌面到碰撞前瞬间，弹簧做的功．‎ ‎(3)从外壳下端离开桌面到上升至h2处，笔损失的机械能．‎ ‎【解析】设外壳上升到h1时速度的大小为v1，外壳与内芯碰撞后瞬间的共同速度大小为v2．‎ ‎(1)对外壳和内芯，从撞后达到共同速度到上升至h2处，由动能定理得：‎ 解得：．‎ ‎(2)外壳与内芯在碰撞过程中动量守恒，即：‎ ‎4mv1＝(4m＋m)v2‎ 将v2代入得：‎ 设弹簧做的功为W，对外壳应用动能定理有：‎ 将v1代入得：．‎ ‎(3)由于外壳和内芯达到共同速度后上升至高度h2的过程中机械能守恒，只有在外壳和内芯的碰撞中有能量损失，损失的能量 将v1、v2代入得：E损＝5/4mg(h2－h1)．‎ ‎[答案]　‎ 由以上例题可以看出，弹簧类试题的确是培养和训练学生的物理思维、反映和开发学生的学习潜能的优秀试题．弹簧与相连物体构成的系统所表现出来的运动状态的变化，为学生充分运用物理概念和规律(牛顿第二定律、动能定理、机械能守恒定律、动量定理、动量守恒定律)巧妙解决物理问题、施展自身才华提供了广阔空间，当然也是区分学生能力强弱、拉大差距、选拔人才的一种常规题型．因此，弹簧试题也就成为高考物理题中的一类重要的、独具特色的考题．‎