2015高考数学人教A版本（9-3空间点、直线、平面之间的位置关系）一轮复习学案 17页

‎【走向高考】2015届高考数学一轮总复习 9-3空间点、直线、平面之间的位置关系课后强化作业 新人教A版 基础巩固强化 一、选择题 ‎1．(文)已知E、F、G、H是空间内四个点，条件甲：E、F、G、H四点不共面，条件乙：直线EF和GH不相交，则甲是乙成立的(　　)‎ A．充分不必要条件　 　　 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎[答案]　A ‎[解析]　点E、F、G、H四点不共面可以推出直线EF和GH不相交；但由直线EF和GH不相交不一定能推出E、F、G、H四点不共面，例如：EF和GH平行，这也是直线EF和GH不相交的一种情况，但E、F、G、H四点共面．故甲是乙成立的充分不必要条件．‎ ‎(理)在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点，若EF与GH交于点M，则(　　)‎ A．M一定在AC上 B．M一定在BD上 C．M可能在AC上也可能在BD上 D．M不在AC上，也不在BD上 ‎[答案]　A ‎[解析]　点M在平面ABC内，又在平面ADC内，故必在交线AC上．‎ ‎2．(文)若直线l不平行于平面α，且l⊄α，则(　　)‎ A．α内的所有直线与l异面 B．α内不存在与l平行的直线 C．α内存在唯一的直线与l平行 D．α内的直线与l都相交 ‎[答案]　B ‎[解析]　由题意知直线l与平面α相交，不妨设直线l∩α＝M，对A，在α内过M点的直线与l不异面，A错误；对B，假设存在与l平行的直线m，则由m∥l得l∥α，这与l∩α＝M矛盾，故B正确，C错误；对D，α内存在与l异面的直线，故D错误．综上知选B.‎ ‎(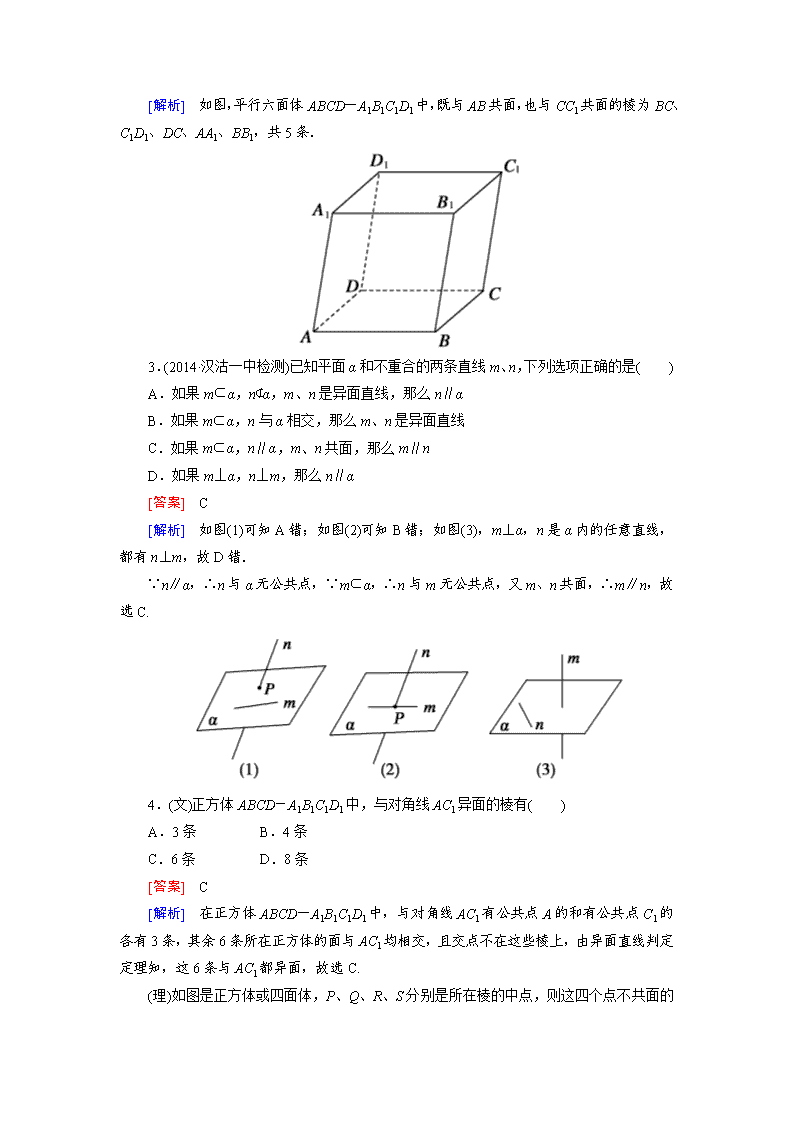理)平行六面体ABCD－A1B‎1C1D1中，既与AB共面也与CC1共面的棱的条数为(　　)‎ A．3　　　　 B．4　　　　‎ C．5　　　　 D．6‎ ‎[答案]　C ‎[解析]　如图，平行六面体ABCD－A1B‎1C1D1中，既与AB共面，也与CC1共面的棱为BC、C1D1、DC、AA1、BB1，共5条．‎ ‎3．(2014·汉沽一中检测)已知平面α和不重合的两条直线m、n，下列选项正确的是(　　)‎ A．如果m⊂α，n⊄α，m、n是异面直线，那么n∥α B．如果m⊂α，n与α相交，那么m、n是异面直线 C．如果m⊂α，n∥α，m、n共面，那么m∥n D．如果m⊥α，n⊥m，那么n∥α ‎[答案]　C ‎[解析]　如图(1)可知A错；如图(2)可知B错；如图(3)，m⊥α，n是α内的任意直线，都有n⊥m，故D错．‎ ‎∵n∥α，∴n与α无公共点，∵m⊂α，∴n与m无公共点，又m、n共面，∴m∥n，故选C.‎ ‎4．(文)正方体ABCD－A1B‎1C1D1中，与对角线AC1异面的棱有(　　)‎ A．3条　　　 B．4条　　　‎ C．6条　　　 D．8条 ‎[答案]　C ‎[解析]　在正方体ABCD－A1B‎1C1D1中，与对角线AC1有公共点A的和有公共点C1的各有3条，其余6条所在正方体的面与AC1均相交，且交点不在这些棱上，由异面直线判定定理知，这6条与AC1都异面，故选C.‎ ‎(理)如图是正方体或四面体，P、Q、R、S 分别是所在棱的中点，则这四个点不共面的一个图是(　　)‎ ‎[答案]　D ‎[解析]　A中，PS∥QR；B中如图可知此四点共面；C中PS∥QR；D中RS在经过平面PQS内一点和平面PQS外一点的直线上，故选D.‎ ‎5．(2013·南昌第一次模拟)设a，b是夹角为30°的异面直线，则满足条件“a⊂α，b⊂β，且α⊥β”的平面α，β(　　)‎ A．不存在 B．有且只有一对 C．有且只有两对 D．有无数对 ‎[答案]　D ‎[解析]　过直线a的平面α有无数个．当平面α与直线b平行时，两直线的公垂线与b确定的平面β⊥α；当平面α与b相交时，过交点作平面α的的垂线与b确定的平面β⊥α，∵平面α有无数个，∴满足条件的平面α、β有无数对，故选D.‎ ‎6．(文)(2013·惠州调研)已知m、n是两条不同直线，α、β、γ是三个不同平面，下列命题中正确的是(　　)‎ A．若m∥α，n∥α，则m∥n 　B．若α⊥γ，β⊥γ，则α∥β C．若m∥α，m∥β，则α∥β 　D．若m⊥α，n⊥α，则m∥n ‎[答案]　D ‎[解析]　当m∥α，n∥α时，m与n可能相交、平行，也可能异面，故A错；B中α⊥γ，β⊥γ时，α与β可能平行，也可能相交，如长方体交于同一个顶点的三个面，故B错；α∩β＝l，m⊄α，m⊄β，m∥l时，满足m∥α，m∥β，故C错；由线面垂直的性质知，⇒m∥n.‎ ‎(理)(2013·广东)设l为直线，α，β是两个不同的平面．下列命题中正确的是(　　)‎ A．若l∥α，l∥β，则α∥β B．若l⊥α，l⊥β，则α∥β C．若l⊥α，l∥β，则α∥β D．若α⊥β，l∥α，则l⊥β ‎[答案]　B ‎[解析]　画出一个长方体ABCD－A1B‎1C1D1.对于A，C1D1∥平面ABB‎1A1，C1D1∥平面ABCD，但平面ABB‎1A1与平面ABCD相交；对于C，BB1⊥平面ABCD，BB1∥平面ADD‎1A1，但平面ABCD与平面ADD‎1A1相交；对于D，平面ABB‎1A1⊥平面ABCD，CD∥平面ABB‎1A1，但CD⊂平面ABCD.‎ 二、填空题 ‎7．在图中，G、H、M、N分别是正三棱柱的顶点或所在棱的中点，则使直线GH、MN是异面直线的图形有________．(填上所有正确答案的序号)‎ ‎[答案]　②④‎ ‎[解析]　图①中，直线GH∥MN；‎ 图②中，G、H、N三点在三棱柱的侧面上，MG与这个侧面相交于G，∴M∉平面GHN，‎ 因此直线GH与MN异面；‎ 图③中，连接MG，GM∥HN，因此GH与MN共面；‎ 图④中，G、M、N共面，但H∉平面GMN，‎ 因此GH与MN异面．‎ 所以图②、④中GH与MN异面．‎ ‎8．如图，直三棱柱ABC－A1B‎1C1中，AB＝1，BC＝2，AC＝，AA1＝3，M为线段BB1上的一动点，则当AM＋MC1最小时，△AMC1的面积为________．‎ ‎[答案]　 ‎[解析]　将三棱柱的侧面A1ABB1和B1BCC1以BB1为折痕展平到一个平面α上，在平面α内AC1与BB1相交，则交点即为M点，易求BM＝1，∴AM＝，MC1＝2，‎ 又在棱柱中，AC1＝，‎ ‎∴cos∠AMC1＝＝＝－，‎ ‎∴∠AMC1＝120°，‎ ‎∴S△AMC1＝AM·MC1·sin∠AMC1‎ ‎＝××2×＝.‎ ‎9．(文)‎ 如图所示，已知正三棱柱ABC－A1B‎1C1的各条棱长都相等，M是侧棱CC1的中点，则异面直线AB1和BM所成的角的大小是________．‎ ‎[答案]　90°‎ ‎[解析]　取BC的中点N，连接AN，则AN⊥平面BCC1B1，‎ ‎∵BM⊂平面BCC1B1，∴AN⊥BM，‎ 又在正方形BCC1B1中，M、N分别为CC1与BC的中点，∴B1N⊥BM，又B1N∩AN＝‎ N，‎ ‎∴BM⊥平面AB1N，∴BM⊥AB1，‎ ‎∴AB1与BM所成的角是90°.‎ ‎(理)在三棱锥P－ABC中，PA⊥底面ABC，AC⊥BC，PA＝AC＝BC，则直线PC与AB所成角的大小是________．‎ ‎[答案]　60°‎ ‎[解析]　‎ 分别取PA、AC、CB的中点F、D、E连接FD、DE、EF、AE，则∠FDE是直线PC与AB所成角或其补角．‎ 设PA＝AC＝BC＝‎2a，在△FDE中，易求得FD＝a，DE＝a，FE＝a，‎ 根据余弦定理，得cos∠FDE＝＝－，‎ 所以∠FDE＝120°.‎ 所以PC与AB所成角的大小是60°.‎ 三、解答题 ‎10．(文)已知在正方体ABCD－A′B′C′D′中，M、N分别是A′D′、A′B′的中点，在该正方体中是否存在过顶点且与平面AMN平行的平面？若存在，试作出该平面，并证明你的结论；若不存在，请说明理由．‎ ‎[分析]　假设存在经过B点与平面AMN平行的平面α，则平面A′B′C′D′与这两平行平面的交线应平行，由于M、N分别为A′D′、A′B′的中点，∴取C′D′的中点F，B′C′的中点E，则MN∥EF，可证明平面BDFE∥平面AMN，过其他点的截面同理可分析找出．‎ ‎[解析]　存在．与平面AMN平行的平面有以下三种情况(E、F分别为所在棱的中点)：‎ 下面以图(1)为例进行证明．‎ ‎∵四边形ABEM是平行四边形，∴BE∥AM，‎ 又BE⊂平面BDE，AM⊄平面BDE，‎ ‎∴AM∥平面BDFE.‎ ‎∵MN是△A′B′D′的中位线，∴MN∥B′D′，‎ ‎∵四边形BDD′B′是平行四边形，‎ ‎∴BD∥B′D′，∴MN∥BD，‎ 又BD⊂平面BDE，MN⊄平面BDE，‎ ‎∴MN∥平面BDFE，‎ 又AM⊂平面AMN，MN⊂平面AMN，且AM∩MN＝M，‎ ‎∴由平面与平面平行的判定定理可得，平面AMN∥平面BDFE.‎ ‎(理)‎ 如图所示，在长方体ABCD－A1B‎1C1D1中，AB＝AD＝1，AA1＝2，M是棱CC1的中点．‎ ‎(1)求异面直线A‎1M和C1D1所成的角的正切值；‎ ‎(2)证明：平面ABM⊥平面A1B‎1M.‎ ‎[解析]　方法1：(1)如图，因为C1D1∥B‎1A1，所以∠MA1B1为异面直线A‎1M与C1D1所成的角．‎ 因为A1B1⊥平面BCC1B1，所以∠A1B‎1M＝90°，‎ 而A1B1＝1，B‎1M＝＝，故 tan∠MA1B1＝＝.‎ 即异面直线A‎1M和C1D1所成的角的正切值为.‎ ‎(2)证明：由A1B1⊥平面BCC1B1，BM⊂平面平面BCC1B1，得A1B1⊥BM①‎ 由(1)知，B‎1M＝，‎ 又BM＝＝，B1B＝2，‎ 所以B‎1M2‎＋BM2＝B1B2，从而BM⊥B‎1M②‎ 又A1B1∩B‎1M＝B1，∴BM⊥平面A1B‎1M，而BM⊂平面ABM，因此平面ABM⊥平面A1B‎1M.‎ 方法2：以A为原点，，，的方向分别作为x、y、z轴的正方向，建立如图所示的空间直角坐标系，则A(0,0,0)，B(1,0,0)，A1(0,0,2)，B1(1,0,2)，C1(1,1,2)，D1(0,1,2)，M(1,1,1)．‎ ‎(1)＝(1,1，－1)，＝(－1,0,0)，‎ cos〈，〉＝＝－.‎ 设异面直线A‎1M与C1D1所成角为α，则cosα＝，‎ ‎∴tanα＝.‎ 即异面直线A‎1M和C1D1所成的角的正切值是.‎ ‎(2)证明：＝(1,0,0)，＝(0,1,1)，＝(0,1，－1)，·＝0，·＝0，‎ ‎∴⊥，⊥，即BM⊥A1B1，BM⊥B‎1M，‎ 又B‎1M∩A1B1＝B1，‎ ‎∴BM⊥平面A1B‎1M，而BM⊂平面ABM，‎ 因此ABM⊥平面A1B‎1M.‎ 能力拓展提升 一、选择题 ‎11．(文)(2014·雅礼中学月考)l1、l2、l3是空间三条不同的直线，则下列命题正确的是(　　)‎ A．l1⊥l2，l2⊥l3⇒l1∥l3‎ B．l1⊥l2，l2∥l3⇒l1⊥l3‎ C．l1∥l2∥l3⇒l1、l2、l3共面 D．l1、l2、l3共点⇒l1、l2、l3共面 ‎[答案]　B ‎[解析]　举反例，由教室内共点的三条墙角线可知A、D是错误的；由三棱柱的三条侧棱可知C是错误的．故选B.‎ ‎(理)(2014·荆州中学月考)如图，在正方体ABCD－A1B‎1C1D1中，M，N分别是BC1、CD1的中点，则下列判断错误的是(　　)‎ A．MN与CC1垂直 B．MN与AC垂直 C．MN与BD平行 D．MN与A1B1平行 ‎[答案]　D ‎[解析]　由于C1D1与A1B1平行，MN与C1D1是异面直线，所以MN与A1B1是异面直线，故选项D错误．‎ ‎[点评]　取CD中点Q，BC中点R，则NQ綊D1D，MR綊CC1，∵CC1綊D1D，∴NQ綊 MR，∴MN∥QR，∵QR∥BD，AC⊥BD，∴AC⊥MN，∴B正确；∵MN∥QR，QR∥BD，∴MN∥BD，∴C正确；∵CC1⊥平面ABCD，∴CC1⊥PQ，∴CC1⊥MN，∴A正确．‎ ‎12．(2012·山西联考)已知直线m、n与平面α、β，下列命题中正确的是(　　)‎ A．m∥β，α∥β，则m∥α B．平面α内不共线三点到平面β的距离相等，则α∥β C．α∩β＝m，n⊥m且α⊥β，则n⊥α D．m⊥α，n⊥β且α⊥β，则m⊥n ‎[答案]　D ‎[解析]　当m⊂α时，也可满足m∥β，α∥β，故①错；‎ 当α∩β＝l，三点A、B、C位于l的两侧，AB∥l，直线AB到l的距离与点C到l的距离相等时，满足A、B、C三点到平面β的距离相等，故②错；‎ 由面面垂直的性质知，C错，因为只有在满足n⊂β内时，才能由n⊥m得出n⊥α的结论；‎ ⇒m⊥n，故D正确．‎ 二、填空题 ‎13．(2013·武汉武昌区联考)已知直线l⊥平面α，直线m⊂平面β，有下列命题：‎ ‎①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β；④l⊥m⇒α∥β.‎ 其中正确命题的序号是________．‎ ‎[答案]　①③‎ ‎[解析]　①正确，∵l⊥α，α∥β，∴l⊥β，又m⊂β，∴l⊥m；②错误，l，m还可以垂直，斜交或异面；③正确，∵l⊥α，l∥m，∴m⊥α，又m⊂β，∴α⊥β；④错误，α与β可能相交．‎ ‎14．(2013·贵阳一模)在正方体ABCD－A1B‎1C1D1中，M，N分别为A1B1，BB1的中点，则异面直线AM与CN所成角的余弦值为________．‎ ‎[答案]　 ‎[解析]　如图，取AB的中点E，连接B1E，则AM∥B1E，取EB的中点F，连接FN，则B1E∥FN，因此AM∥FN，则直线FN与CN所夹的锐角或直角为异面直线AM与CN所成的角．‎ 设AB＝1，连接CF，‎ 在△CFN中，CN＝，FN＝，CF＝.‎ 由余弦定理得cos∠CNF＝＝.‎ 三、解答题 ‎15．(2013·江苏)如图，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．‎ 求证：(1)平面EFG∥平面ABC；‎ ‎(2)BC⊥SA.‎ ‎[解析]　(1)因为AS＝AB，AF⊥SB，垂足为F，所以F是SB的中点．又因为E是SA的中点，所以EF∥AB.‎ 因为EF⊄平面ABC，AB⊂平面ABC，‎ 所以EF∥平面ABC.‎ 同理EG∥平面ABC.‎ 又EF∩EG＝E，‎ 所以平面EFG∥平面ABC.‎ ‎(2)因为平面SAB⊥平面SBC，且交线为SB，‎ 又AF⊂平面SAB，AF⊥SB，‎ 所以AF⊥平面SBC，‎ 因为BC⊂平面SBC，所以AF⊥BC.‎ 又因为AB⊥BC，AF∩AB＝A，AF，AB⊂平面SAB，所以BC⊥平面SAB.‎ 因为SA⊂平面SAB，所以BC⊥SA.‎ 考纲要求 理解空间直线、平面位置关系的定义，并了解可以作为推理依据的公理和定理．‎ 补充说明 ‎1．异面直线的判定主要用定理法、反证法 ‎(1)定理法：过平面内一点与平面外一点的直线与平面内不经过该点的直线为异面直线(此结论可作为定理使用)．‎ ‎(2)反证法：先假设两条直线不是异面直线，即两直线平行或相交，由假设的条件出发，经过严密的推理，导出矛盾，从而否定假设，肯定两条直线异面．‎ ‎2．求异面直线所成的角主要用平移法，其一般步骤为 ‎(1)平移：选取适当的点，平移异面直线的一条(或两条)成相交直线．‎ ‎(2)证明：证明所作的角是异面直线所成的角．‎ ‎(3)求解：找出含有此角的三角形，并解之．‎ ‎(4)取舍：根据异面直线所成角的范围确定大小．‎ ‎3．共线与共面问题 证明共线时，所共的直线一般定位为两个平面的交线；证明共面问题时，一般先由已知条件确定一个平面(有平行直线的先用平行直线确定平面)，再证其他元素在该平面内．‎ ‎4．求异面直线所成角 异面直线所成角的大小，是用过空间任意一点分别引它们的平行线所成的锐角(或直角)来定义的．因此，平移直线是求异面直线所成角的关键．这里给出几种平移直线的途径．‎ ‎(1)在已知平面内平移直线构造可解的三角形，或根据实际情况构造辅助平面，在辅助平面内平移直线构造可解的三角形，是求异面直线所成角的途径之一；‎ 这种方法常常是取两条异面直线中的一条和另一条上一点确定一个平面，在这个平面内过这个点作这条直线的平行线，或在两条异面直线上各选一点连线，构造两个辅助面过渡．‎ ‎[例1]　如图所示，在正方体AC1中，M、N分别是A1B1、BB1的中点，求异面直线AM和CN所成角的余弦值．‎ ‎[解析]　在平面ABB‎1A1内作EN∥AM交AB于E，则EN与CN所成的锐角(或直角)即为AM和CN所成的角．设正方体棱长为a.‎ 在△CNE中，可求得CN＝a，NE＝a，CE＝a，由余弦定理得，cos∠CNE＝＝.‎ 即异面直角AM与CN所成角的余弦值为.‎ ‎(2)利用平行平面平移直线构成可解的三角形，是求异面直线所成角的途径之二；‎ 这种方法常见于两条异面直线分别在两个互相平行的平面内，可利用面面平行的性质，将一条直线平移到另一条所在的平面内．‎ ‎[例2]　如图所示，正方体AC1中，B1E1＝D‎1F1＝，求BE1与DF1所成角的余弦值．‎ ‎[解析]　∵平面ABB‎1A1∥平面DCC1D1，∴在A1B1上取H，使A1H＝，即可得：AH∥DF1.引NH∥BE1，则锐角∠AHN就是DF1与BE1所成的角．‎ 设正方体棱长为a，在△AHN中，易求得：‎ AN＝，AH＝NH＝BE1＝a.‎ 由余弦定理得，cos∠AHN＝＝.‎ 即BE1与DF1所成的角的余弦值为.‎ ‎(3)整体平移几何体，构造可解的三角形，是求异面直线所成角的途径之三．‎ 这种方法常常是将原有几何体上再拼接上同样的一个几何体(相当于将原几何体作了一个平移)创造平移直线的条件．‎ ‎[例3]　如下图长方体AC1中，AB＝12，BC＝3，AA1＝4，N在A1B1上，且B1N＝4.求BD1与C1N所成角的余弦值．‎ ‎[解析]　如图所示，将长方体AC1平移到BCFE－B‎1C1F1E1的位置，则C1E∥BD1，C1E与C1N所成的锐角(或直角)就是BD1与C1N所成的角．‎ 在△NC1E中，根据已知条件可求B1N＝4，C1N＝5，C1E＝13，EN＝＝4.‎ 由余弦定理，得cos∠NC1E＝＝－.‎ ‎∴BD1与C1N所成角的余弦值为.‎ 备选习题 ‎1．空间中一条线段AB的三视图中，俯视图是长度为1的线段，侧视图是长度为2的线段，则线段AB的长度的取值范围是(　　)‎ A．(0,2] B．[2，]‎ C．[2,3] D．[2，]‎ ‎[答案]　B ‎[解析]　以线段AB为体对角线构造长方体，设长方体的长、宽、高分别为x、y、z，则由题意知，∴AB2＝x2＋y2＋z2＝5－y2，‎ ‎∵x2>0，∴1－y2>0，∴0