全国统一高考数学真题及逐题详细解析文科—海南卷 19页

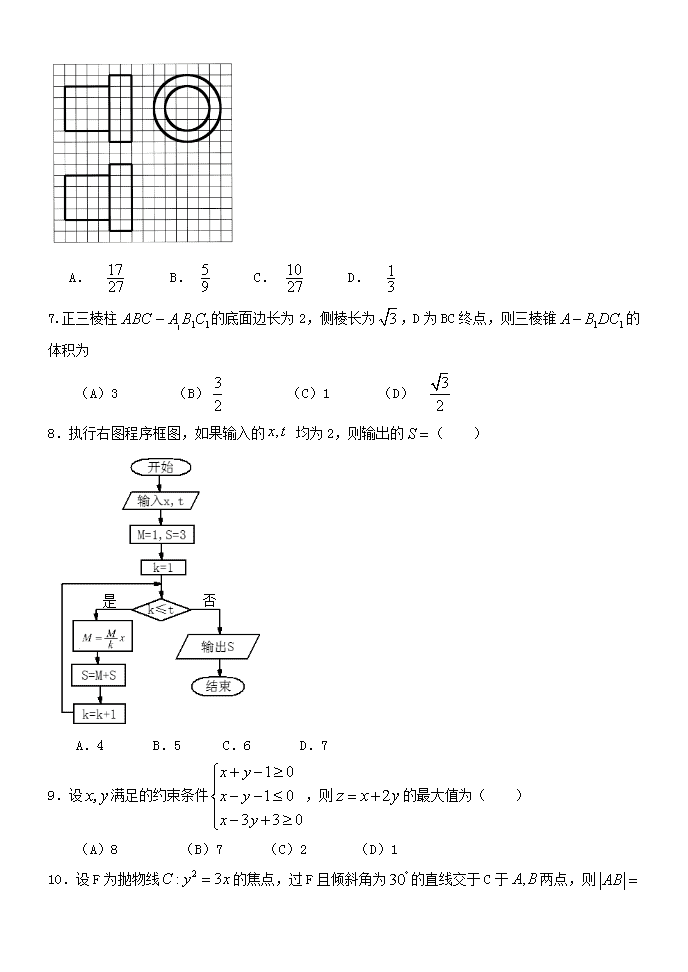
‎2014年普通高等学校招生全国统一考试 海南数学文科（新课标卷Ⅱ）‎ 第Ⅰ卷 一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合 ，，则（ ）‎ A. B. C. D.‎ ‎2.（ ）‎ A. B. C. D.‎ ‎3.函数在 处导数存在，若 ，是的极值点，则（ ）‎ A.是的充分必要条件 B.是的充分条件，但不是的必要条件 C.是的必要条件，但不是的充分条件 D.既不是的充分条件，也不是的必要条件 ‎4.设向量满足，，则 （ ）‎ A.1 B.‎2 C.3 D.5‎ ‎5.等差数列的公差为2，若成等比数列，则的前项和（ ）‎ A. B. C. D.‎ ‎6.如图，网格纸上正方形小格的边长为1（表示‎1cm）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为‎3cm，高为‎6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）‎ A． B． C． D． ‎ ‎7.正三棱柱的底面边长为2，侧棱长为，D为BC终点，则三棱锥的体积为 ‎（A）3 （B） （C）1 （D）‎ ‎8．执行右图程序框图，如果输入的 均为2，则输出的（ ）‎ 是 否 A．4 B．‎5 C．6 D．7‎ ‎9．设满足的约束条件，则的最大值为（ ）‎ ‎（A）8 （B）7 （C）2 （D）1‎ ‎10．设F为抛物线的焦点，过F且倾斜角为的直线交于C于两点，则 ‎（A） （B）6 （C）12 （D）‎ ‎11．若函数在区间单调递增，则的取值范围是 ‎（A） （B） （C） （D）‎ ‎12．设点，若在圆上存在点N，使得,则的取值范围是 ‎（A） （B） （C） （D）‎ 第Ⅱ卷 二、填空题：本大概题共4小题，每小题5分。‎ ‎13．甲、已两名元动员各自等可能地从红、白、蓝3种颜色的运动服种选择1种，则他们选择相同颜色运动服的概率为_______.‎ ‎14．函数的最大值为_________．‎ ‎15．已知偶函数的图像关于直线对称，，则_______.‎ ‎16．数列 满足，，则_________.‎ 三、解答题（本大题共8小题）‎ ‎17.（12分）‎ ‎ 四边形ABCD的内角A与C互补，AB=1，BC=3，CD=DA=2. ‎ ‎ (I) 求C和BD；‎ ‎ (II)求四边形ABCD的面积.‎ ‎18.（12分） 如图，四棱锥P-ABCD中，底面ABCD为矩形，，E为PD中点.‎ ‎ (I)证明:PB平面AEC;‎ ‎ (II)设AP=1，，三棱锥P-ABD的体积，求A到平面PBC的距离. ‎ ‎19. （本小题满分12分）某市为了考核甲、乙两部门的工作情况，随机访问了50位市民。根据这50位市民对这两部门的评分（评分越高表明市民的评价越高），绘制茎叶图如下：‎ 甲部门 乙部门 ‎3‎ ‎5 9‎ ‎4‎ ‎4‎ ‎0 4 4 8‎ ‎9 7‎ ‎5‎ ‎1 2 2 4 5 6 6 7 7 7 8 9‎ ‎9 7 6 6 5 3 3 2 1 1 0‎ ‎6‎ ‎0 1 1 2 3 4 6 8 8‎ ‎9 8 8 7 7 7 6 6 5 5 5 5 4 4 4 3 3 3 2 1 0 0‎ ‎7‎ ‎0 0 1 1 3 4 4 9‎ ‎6 6 5 5 2 0 0‎ ‎8‎ ‎1 2 3 3 4 5‎ ‎6 3 2 2 2 0‎ ‎9‎ ‎0 1 1 4 5 6‎ ‎10‎ ‎0 0 0‎ ‎（I）分别估计该市的市民对甲、乙部门评分的中位数；‎ ‎（II）分别估计该市的市民对甲、乙部门的评分高于90的概率；‎ ‎（III）根据茎叶图分析该市的市民对甲、乙两部门的评价。‎ ‎20. （12分）设分别是椭圆的左右焦点，M是C上一点且与x轴垂直，直线与C的另一个交点是N.‎ ‎ (I)若直线MN的斜率为，求C的离心率;‎ ‎ (II)若直线MN在y轴上的截距为2，且，求a，b.‎ ‎21. （12分）已知函数.曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2.‎ ‎ (I) a ;‎ ‎ (II)证明：当时，曲线与直线只有一个交点.‎ ‎22.（10分）选修4-1：几何证明选讲 ‎ 如图，P是外一点，PA是切线，A为切点，割线PBC与相交于点B，C，PC=2PA，D为PC中点，AD的延长线交于点E，证明：‎ ‎ (I) BE=EC ‎ (II) ‎ ‎23. （10分）选修4-4：坐标系与参数方程 ‎ 在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，半圆C的极坐标方程为 ‎ .‎ ‎ (I)求C的参数方程 ‎ (II)设点D在C上，C在D处的切线与直线垂直，根据(I)中你得到的参数方程，确定D的坐标. ‎ ‎24. （10分）选修4-5：不等式选讲 ‎ 设函数.‎ ‎ (I)证明：‎ ‎ (II)若，求a的取值范围.‎ 参考答案 一、选择题 ‎1．B.‎ 解析：把-2，0，2代人验证，只有2满足不等式，故选B. ‎ 考点：考查集合的知识，简单题.‎ ‎2．B.‎ 解析： ‎ 故选B.‎ 考点：考查复数的基本知识，简单题.‎ ‎3．C.‎ 解析：极值点必为导函数的根，而导函数的根不一定是极值点，即 ‎ 从而p是q的必要但不充分的条件 故选C.‎ 考点：考查充要条件与极值的基础知识，简单题.‎ ‎4．A．‎ 解析：‎ 故选A． ‎ 考点：考查平面向量的数量积，中等题.‎ ‎5．A．‎ 解析：∵数列是等差数列，公差等于2 ‎ ‎∴ ‎ ‎∵ 成等比数列 ‎∴ ‎ 解得 ‎ ‎∴ ‎ 故选A．‎ 考点：考查等差数列的通项公式与求和公式，中等题.‎ ‎6．C.‎ 解析：毛胚的体积 制成品的体积 ‎ ‎∴切削掉的体积与毛胚体积之比为：‎ ‎ ，故选C.‎ 考点：考查三视图于空间几何体的体积，中等题.‎ ‎7．C.‎ 解析： ∵正三棱柱的底面边长为2，D 为BC中点 ‎∴ ‎ ‎∵ ‎ ‎∴ ‎ ‎∴ .故选C.‎ 考点：考查空间点，线，面关系和棱锥体积公式，中等题.‎ ‎8．D.‎ 解析：‎ 第1次循环M=2,S=5,k=1‎ 第2次循环，M=2,S=7,k=2‎ 第3次循环k=3>2,故输出S=7，故选D.‎ 考点：考查算法的基本知识，简单题.‎ ‎9．A．‎ 解析：作图即可.‎ 考点：考查二元一次不等式组的应用，中等题.‎ ‎10．C.‎ 解析：∵ ‎ ‎∴抛物线C的焦点的坐标为： ‎ 所以直线AB的方程为： ‎ 故 ‎ 从而 ‎ ‎∴弦长 ‎ 故选C.‎ 考点：考查抛物线的几何性质，弦长计算以及分析直线和圆锥曲线位置关系的能力，难度为中等题.‎ ‎11．D.‎ 解析： ‎ ‎ ‎ 在区间上递增 在区间上恒大于等于0，‎ ‎ ‎ ‎ ‎ 故选D.‎ 考点：考查导数与函数单调性的关系.中等题.‎ ‎12．A．‎ 解析：设N点的坐标为 ‎ ‎（1）当 时 ‎∵ ‎ ‎∴OM,MN的斜率分别为： ‎ ‎∵ ‎ ‎∴ ‎ 即 ‎ 取正号时，化简（*）式得： ‎ 取负号化简（*）式得：‎ ‎∴ ‎ ‎∴‎ 故 且 ‎ ‎（2）当时，取,此时满足题设.‎ ‎（3）当时，取，此时也满足题设.‎ 综上所述， ，故选A．‎ 从上面解法可以看到选择N的几个特殊位置观察，即可以猜出答案，这样就可以简化解法.‎ 考点：考查应用斜率与倾斜角的概念，直线方程，园的方程,分析问题的能力.困难题.‎ 二、填空题 ‎13． ‎ 解析： ‎ 考点：考查古典概型的概念.简单题.‎ ‎14．1‎ 解析：因为 ‎ ‎ 所以最大值为1.‎ 考点：考查和差角公式，简单题. ‎ ‎15．3‎ 解析：因是偶函数，所以 ，因关于，所以 .‎ 考点：考查偶函数的概念，轴对称的概念.简单题.‎ ‎16． ‎ 解析：∵ ，‎ ‎∴ ‎ 考点：考查递推数列的概念，简单题.‎ 三、解答题 ‎17．解析：（I） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎(II)由（I） 得，四边形ABCD的面积S= ‎ ‎ ‎ 考点：考查余弦定理的应用，中等题.‎ ‎18．解析：(I)连接EF,因为四边形ABCD是矩形，故F为AC中点，又因为E为PD中点，故EF是△PBD的中位线，从而 ,故 ‎ ‎(II)设AB=a，因 ‎ 则 ‎ 所以 ‎ 过A作AG垂直PB于G.‎ 因为 ‎ 又因为 ‎ 所以 ,又 ‎ 故 ‎ ‎ 所以AG为点A到面PBC的距离.‎ 因 ‎ 所以 ‎ 故点A到面PBC的距离为.‎ 考点：考查空间点线面的位置关系与空间距离.中等题.‎ ‎19．解析：(I)甲部门的得分共50个，50个数字从小到大排列起来位于中间位置的数为第25，第26个数，它们分别是：75，75，故甲部门得分的中位数是75.‎ 乙部门的得分也是50个数，它们从小到大排列起来的第25，26个数字分别是：66，68，故乙部门的中为数为.‎ ‎(II)市民对甲，乙两部门的评分各有n=50个，对甲部门评分高于90分的分数有m=5个，对乙部门的评分高于90分的s=8个，故对甲部门评分高于90分的概率为，对乙部门的评分高于90的概率为.‎ ‎（III）观察茎叶图的形状，甲的分数在茎6，7处形成单峰，出现在这里面的数据频率为，其中位数为75，乙的分数在茎5，6，7处形成单峰，出现在这个单峰里面的数据频率为，中位数为67.因为>,75>67,这说明市民对甲部门的评价基本在75分附近，对乙部门的评价基本在67分左右.整体看市民对甲部门的评价更好.‎ 考点：考查使用茎叶图及样本的数字特征估计总体的能力，中等题.‎ ‎20．解析：（I）∵（不妨设M在x轴的上方）‎ ‎∴M的坐标满足方程组 ‎ ‎∵MN的斜率为 ‎ ‎∴‎ ‎∵ ‎ 又∵ ‎ ‎∴椭圆离心率为 .‎ ‎(II)∵MN在y轴上的截距为2，O为的中点 ‎∴M的坐标为(c,4)(不妨设M在x轴的上方)‎ 由（I）得 (*)‎ ‎∵ ‎ ‎∴‎ 作于T,由于△∽ △ ,故有 ‎ ‎∴ ，即 ‎ 把N点的坐标代人椭圆方程得：‎ ‎∴ ‎ 把（*）与（**）联立得： ‎ 考点：考查椭圆的几何性质以及直线与椭圆的位置关系，难题.‎ ‎21．解析：（I） ‎ ‎∵切点为(0,2),切线过点（-2，0）‎ ‎∴切线的斜率为 ‎∴ ‎ ‎(II)由（I）知，，故 ‎ 记 ，‎ ‎∴ ‎ ‎∴ ‎ ‎（1）当时 ‎ ‎ 由，‎ ‎ ‎ ‎∴ ‎ ‎∴ 或 ‎ ‎ ‎ ‎∴在区间 上递增，在区间上递减 ‎ ‎∴的极小值为 ‎∵‎ ‎∴ ‎ 记 ‎ 由，由 ‎ ‎∴ ‎ ‎∴在区间递减 ‎ ‎∴ （∵是减区间）‎ 又∵‎ ‎∴当时，方程只有一根.‎ ‎ (2) 当时，‎ 有，从而在R上递增 ‎∵，‎ ‎∴当时，方程只有一根.‎ 综上所述，方程在R上只有一根，即曲线直线只有唯一交点. ‎ 考点：考查利用导数综合研究函数性质的能力，难度压轴题.‎ ‎22．解析：(I)连接OA,OD交BC于F,设，因PA是的切线，则 ‎ ‎∵ ‎ ‎∴是等腰三角形 ‎∴ ‎ ‎∵‎ ‎∴故OE平分弧BC ,从而BE = EC.‎ ‎(II)∵ ‎ ‎∴‎ 由（I）知 ‎∴ ‎ ‎∴‎ ‎ ‎ ‎ ‎ 把代人上式，得 ‎ ‎∴ ‎ 考点：考查与园有关的角的知识和圆幂定理的应用.难度中等.‎ ‎23．解析：（I）∵极坐标方程为 ‎ ‎∴‎ ‎∴对应的普通方程为： ，即 ‎ ‎∴对应的参数方程为 ‎ ‎(II)设半圆的圆心为A，则A(1,0),又由（I）知，可以设D点坐标为 ‎ ‎∴直线DA的斜率 ‎ ‎∵切线与直线垂直 ‎∴ ‎ ‎∴ 即D点坐标为 ‎ 考点：本题考查园的极坐标方程参数方程以及参数方程的简单应用，难度中等题.‎ ‎24．解析：（I）∵ ‎ ‎∴ ‎ ‎∴在递增，在递减，在上为常数 ‎∴的最小值为 ‎∴‎ （II） ‎（1）当时， ‎ ‎∴ ‎ ‎∴ ‎ ‎（2）当时， ‎ ‎∴ 或 故 综上所述 ‎ 考点：考查带有绝对值的不等式的应用能力，考查函数与不等式的关系，中等题.‎