湖南省十三校联考高考数学二模试卷文科解析 24页

‎2016年湖南省十三校联考高考数学二模试卷（文科）‎ ‎　‎ 一、选择题 ‎1．i是虚数单位，若=a+bi（a，b∈R），则a+b的值是（　　）‎ A．2B．﹣2C．3D．﹣3‎ ‎2．集合A={y∈R|y=lgx，x＞1}，B={﹣2，﹣1，2}则下列结论正确的是（　　）‎ A．A∩B={﹣2，﹣1}B．（CUA）∪B=（﹣∞，0）C．A∪B=（0，+∞）D．（CUA）∩B={﹣2，﹣1}‎ ‎3．已知命题p：∀x＞0，x+≥4：命题q：∃x0∈R+，2x0=，则下列判断正确的是（　　）‎ A．p是假命题B．q是真命题C．p∧（￢q）是真命题D．（￢p）∧q是真命题 ‎4．已知函数f（x）=sinωx（x∈R，ω＞0）的最小正周期为π，为了得到函数g（x）=sin（ωx+）和图象，只要将y=f（x）的图象（　　）‎ A．向左平移个单位长度B．向右平移个单位长度 C．向左平移个单位长度D．向右平移个单位长度 ‎5．下列函数既是奇函数，又在区间[﹣1，1]上单调递减的是（　　）‎ A．f（x）=sinxB．f（x）=﹣|x+1|‎ C．f（x）=D．f（x）=ln ‎6．已知直线l⊥平面α，直线m⊂平面β，有下面四个命题：‎ ‎（1）α∥β⇒l⊥m，（2）α⊥β⇒l∥m，‎ ‎（3）l∥m⇒α⊥β，（4）l⊥m⇒α∥β，‎ 其中正确命题是（　　）‎ A．（1）与（2）B．（1）与（3）C．（2）与（4）D．（3）与（4）‎ ‎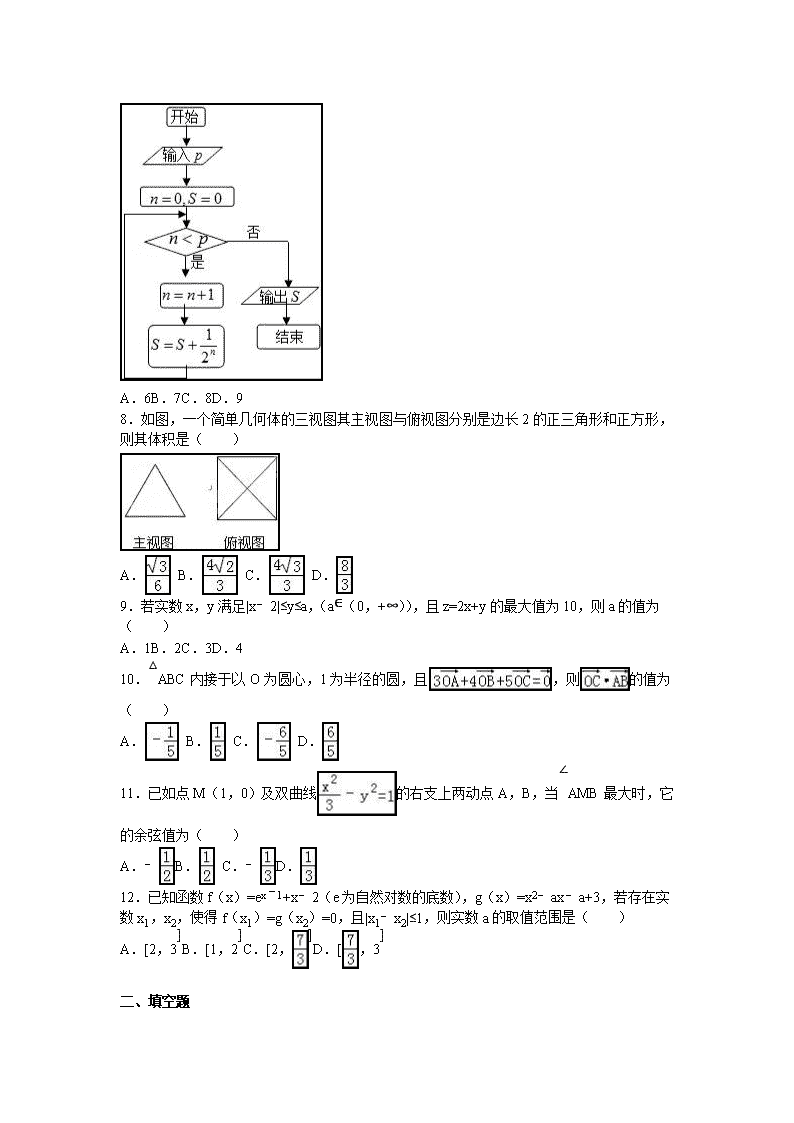7．执行如图的程序框图，若输出，则输入p=（　　）‎ A．6B．7C．8D．9‎ ‎8．如图，一个简单几何体的三视图其主视图与俯视图分别是边长2的正三角形和正方形，则其体积是（　　）‎ A． B． C． D．‎ ‎9．若实数x，y满足|x﹣2|≤y≤a，（a∈（0，+∞）），且z=2x+y的最大值为10，则a的值为（　　）‎ A．1B．2C．3D．4‎ ‎10．△ABC内接于以O为圆心，1为半径的圆，且，则的值为（　　）‎ A． B． C． D．‎ ‎11．已如点M（1，0）及双曲线的右支上两动点A，B，当∠AMB最大时，它的余弦值为（　　）‎ A．﹣B． C．﹣D．‎ ‎12．已知函数f（x）=ex﹣1+x﹣2（e为自然对数的底数），g（x）=x2﹣ax﹣a+3，若存在实数x1，x2，使得f（x1）=g（x2）=0，且|x1﹣x2|≤1，则实数a的取值范围是（　　）‎ A．[2，3]B．[1，2]C．[2，]D．[，3]‎ ‎　‎ 二、填空题 ‎13．某小卖部为了了解热茶销售量y（杯）与气温x（℃）之间的关系，随机统计了某4天卖出的热茶的杯数与当天气温，并制作了对照表：‎ 气温（℃）‎ ‎18‎ ‎13‎ ‎10‎ ‎﹣1‎ 杯数 ‎14‎ ‎24‎ ‎28‎ ‎54‎ 由表中数据算得线性回归方程=bx+a中的b≈﹣2，预测当气温为﹣5℃时，热茶销售量为　　　　　　杯．‎ ‎14．设函数f（x）满足，则f（2）=　　　　　　．‎ ‎15．在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，三边a、b、c成等差数列，且B=，则（cosA一cosC）2的值为　　　　　　．‎ ‎16．在平面直角坐标系xOy中，已知圆C：x2+（y﹣4）2=4，点A是x轴上的一个动点，直线AP，AQ分别切圆C于P，Q两点，则线段PQ长的取值范围为　　　　　　．‎ ‎　‎ 三、解答题 ‎17．已知数列{an}中，a1=1，前n项和Sn=an（n≥2，n∈N*）．‎ ‎（I）求a2，a3及{an}的通项公式；‎ ‎（Ⅱ）记bn=an+，cn=，求数列{cn}的前n项和Tn．‎ ‎18．某单位开展岗前培训．期间，甲、乙2人参加了5次考试，成绩统计如下：‎ 第一次 第二次 第三次 第四次 第五次 甲的成绩 ‎82‎ ‎82‎ ‎79‎ ‎95‎ ‎87‎ 乙的成绩 ‎95‎ ‎75‎ ‎80‎ ‎90‎ ‎85‎ ‎（Ⅰ）根据有关统计知识，回答问题：若从甲、乙2人中选出1人上岗，你认为选谁合适，请说明理由；‎ ‎（Ⅱ）根据有关概率知识，解答以下问题：‎ ‎①从甲、乙2人的成绩中各随机抽取一个，设抽到甲的成绩为x，抽到乙的成绩为y．用A表示满足条件|x﹣y|≤2的事件，求事件A的概率；‎ ‎②若一次考试两人成绩之差的绝对值不超过3分，则称该次考试两人“水平相当”．由上述5次成绩统计，任意抽查两次考试，求至少有一次考试两人“水平相当”的概率．‎ ‎19．如图，在四棱锥O﹣ABCD中，底面ABCD是边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点．‎ ‎（Ⅰ）求异面直线AB与MD所成角的大小；‎ ‎（Ⅱ）求点B到平面OCD的距离．‎ ‎20．已知曲线C1： +=1（a＞b＞0）所围成的封闭图形的面积为4，曲线C1的内切圆半径为，记C2为以曲线C1与坐标轴的交点为顶点的椭圆．‎ ‎（1）求椭圆C2的标准方程；‎ ‎（2）设AB是过椭圆C2中心O的任意弦，M是椭圆上一点，且满足（+）•=0，求△AMB的面积的最小值．‎ ‎21．已知函数f（x）=ax2﹣lnx．‎ ‎（I）讨论函数f（x）单调性；‎ ‎（Ⅱ）当时，证明：曲线y=f（x）与其在点P（t，f（t））处的切线至少有两个不同的公共点．‎ ‎　‎ ‎[选修4-4：几何证明选讲]‎ ‎22．如图，⊙O是△ABC的外接圆，D是的中点，BD交AC于点E．‎ ‎（1）求证：CD2﹣DE2=AE•EC；‎ ‎（2）若CD的长等于⊙O的半径，求∠ACD的大小．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎23．选修4﹣4：坐标系与参数方程．‎ 极坐标系与直角坐标系xoy有相同的长度单位，以原点为极点，以x轴正半轴为极轴，已知曲线C1的极坐标方程为ρ=4cosθ，曲线C2的参数方程为（t为参数，0≤α＜π），射线θ=φ，θ=φ+，θ=φ﹣与曲线C1交于（不包括极点O）三点A、B、C．‎ ‎（I）求证：|OB|+|OC|=|OA|；‎ ‎（Ⅱ）当φ=时，B，C两点在曲线C2上，求m与α的值．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．设函数f （x）=|x﹣a|+3x，其中a≠0．‎ ‎（1）当a=2时，求不等式f（x）≥3x+2的解集；‎ ‎（2）若不等式f （x）≤0的解集包含{x|x≤﹣1}，求a的取值范围．‎ ‎　‎ ‎2016年湖南省十三校联考高考数学二模试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．i是虚数单位，若=a+bi（a，b∈R），则a+b的值是（　　）‎ A．2B．﹣2C．3D．﹣3‎ ‎【考点】复数代数形式的混合运算．‎ ‎【分析】利用复数的运算法则、复数相等即可得出．‎ ‎【解答】解：∵a+bi====﹣1+3i，‎ ‎∴a=﹣1，b=3，‎ ‎∴a+b=2．‎ 故选：A．‎ ‎　‎ ‎2．集合A={y∈R|y=lgx，x＞1}，B={﹣2，﹣1，2}则下列结论正确的是（　　）‎ A．A∩B={﹣2，﹣1}B．（CUA）∪B=（﹣∞，0）C．A∪B=（0，+∞）D．（CUA）∩B={﹣2，﹣1}‎ ‎【考点】交、并、补集的混合运算．‎ ‎【分析】集合A为对数函数的值域，解出后对照选项逐一验证．‎ ‎【解答】解：依题意，A={y|y＞0}，∵B={﹣2，﹣1，2}，‎ 所以A∩B={﹣2，﹣1}={2}，A错，A∪B=（0，+∞）∪={﹣2，﹣1}，B错，‎ ‎（CUA）∪B═{﹣2，﹣1}，C错，‎ 故选D ‎　‎ ‎3．已知命题p：∀x＞0，x+≥4：命题q：∃x0∈R+，2x0=，则下列判断正确的是（　　）‎ A．p是假命题B．q是真命题C．p∧（￢q）是真命题D．（￢p）∧q是真命题 ‎【考点】命题的真假判断与应用．‎ ‎【分析】利用基本不等式求最值判断命题p的真假，由指数函数的值域判断命题q的真假，然后结合复合命题的真值表加以判断．‎ ‎【解答】解：当x＞0，x+≥，当且仅当x=2时等号成立，‎ ‎∴命题p为真命题，￢P为假命题；‎ 当x＞0时，2x＞1，‎ ‎∴命题q：∃x0∈R+，2x0=为假命题，则￢q为真命题．‎ ‎∴p∧（￢q）是真命题，（￢p）∧q是假命题．‎ 故选：C．‎ ‎　‎ ‎4．已知函数f（x）=sinωx（x∈R，ω＞0）的最小正周期为π，为了得到函数g（x）=sin（ωx+）和图象，只要将y=f（x）的图象（　　）‎ A．向左平移个单位长度B．向右平移个单位长度 C．向左平移个单位长度D．向右平移个单位长度 ‎【考点】函数y=Asin（ωx+φ）的图象变换．‎ ‎【分析】由函数的周期性求得ω=2，可得f（x）=sin2x，再根据根据函数y=Asin（ωx+φ）的图象变换规律，得出结论．‎ ‎【解答】解：由于函数f（x）=sinωx（x∈R，ω＞0）的最小正周期为π，‎ 故有 =π，∴ω=2，‎ ‎∴f（x）=sin2x，‎ 根据函数y=Asin（ωx+φ）的图象变换规律，为了得到函数g（x）=sin（2x+）=sin2（x+）的图象，‎ 只要将y=f（x）的图象向左平移个单位长度即可，‎ 故选：A．‎ ‎　‎ ‎5．下列函数既是奇函数，又在区间[﹣1，1]上单调递减的是（　　）‎ A．f（x）=sinxB．f（x）=﹣|x+1|‎ C．f（x）=D．f（x）=ln ‎【考点】奇偶性与单调性的综合．‎ ‎【分析】分别根据函数奇偶性和单调性的定义和性质进行判断即可得到结论．‎ ‎【解答】解：函数f（x）=sinx，是奇函数，在[﹣1，1]上单调递增，不满足条件．‎ 函数f（x）=﹣|x+1|不是奇函数，不满足条件，‎ 函数f（x）=是偶函数，不满足条件，‎ 故选：D ‎　‎ ‎6．已知直线l⊥平面α，直线m⊂平面β，有下面四个命题：‎ ‎（1）α∥β⇒l⊥m，（2）α⊥β⇒l∥m，‎ ‎（3）l∥m⇒α⊥β，（4）l⊥m⇒α∥β，‎ 其中正确命题是（　　）‎ A．（1）与（2）B．（1）与（3）C．（2）与（4）D．（3）与（4）‎ ‎【考点】空间中直线与平面之间的位置关系．‎ ‎【分析】根据已知直线l⊥平面α，直线m⊂‎ 平面β，结合α∥β结合线面垂直的定义及判定，易判断（1）的真假；结合α⊥β，结合空间直线与直线关系的定义，我们易判断（2）的对错；结合l∥m，根据线面垂直的判定方法及面面平行的判定定理，易判断（3）的正误；再根据l⊥m结合空间两个平面之间的位置关系，易得到（4）的真假，进而得到答案．‎ ‎【解答】解：∵直线l⊥平面α，α∥β，∴l⊥平面β，又∵直线m⊂平面β，∴l⊥m，故（1）正确；‎ ‎∵直线l⊥平面α，α⊥β，∴l∥平面β，或l⊂平面β，又∵直线m⊂平面β，∴l与m可能平行也可能相交，还可以异面，故（2）错误；‎ ‎∵直线l⊥平面α，l∥m，∴m⊥α，∵直线m⊂平面β，∴α⊥β，故（3）正确；‎ ‎∵直线l⊥平面α，l⊥m，∴m∥α或m⊂α，又∵直线m⊂平面β，则α与β可能平行也可能相交，故（4）错误；‎ 故选B．‎ ‎　‎ ‎7．执行如图的程序框图，若输出，则输入p=（　　）‎ A．6B．7C．8D．9‎ ‎【考点】程序框图．‎ ‎【分析】模拟执行程序框图，可得．解得n的值为7，退出循环的条件为7＜p不成立，从而可得p的值．‎ ‎【解答】解：模拟执行程序框图，可得．‎ 解得：n=7．‎ 故当p=7时，n=7＜p，不成立，退出循环，输出S的值为．‎ 故选：B．‎ ‎　‎ ‎8．如图，一个简单几何体的三视图其主视图与俯视图分别是边长2的正三角形和正方形，则其体积是（　　）‎ A． B． C． D．‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】根据主视图、俯视图，可得简单几何体的直观图是底面边长为2，高为的正四棱锥，利用体积公式可得结论．‎ ‎【解答】解：由主视图可知，三棱锥的高为，结合俯视图可得简单几何体的直观图是底面边长为2，高为的正四棱锥 ‎∴体积为=‎ 故选C．‎ ‎　‎ ‎9．若实数x，y满足|x﹣2|≤y≤a，（a∈（0，+∞）），且z=2x+y的最大值为10，则a的值为（　　）‎ A．1B．2C．3D．4‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件|x﹣2|≤y≤a作出可行域，数形结合得到最优解，求出最优解的坐标，代入目标函数后求得a的值．‎ ‎【解答】解：由|x﹣2|≤y≤a，作出可行域如图，‎ 联立，解得A（a+2，a），‎ 化z=2x+y为y=﹣2x+z．‎ 由图可知，当直线y=﹣2x+z过A时，z有最大值，‎ 此时2（a+2）+a=10，解得：a=2．‎ 故选：B．‎ ‎　‎ ‎10．△ABC内接于以O为圆心，1为半径的圆，且，则的值为（　　）‎ A． B． C． D．‎ ‎【考点】平面向量数量积的运算．‎ ‎【分析】将已知等式中的移到等式的一边，将等式平方求出；将利用向量的运算法则用，利用运算法则展开，求出值．‎ ‎【解答】解：∵‎ ‎∴‎ ‎∴=‎ ‎∵A，B，C在圆上 ‎∴OA=OB=OC=1‎ ‎∴‎ ‎∴‎ ‎=‎ ‎=‎ 故选A．‎ ‎　‎ ‎11．已如点M（1，0）及双曲线的右支上两动点A，B，当∠AMB最大时，它的余弦值为（　　）‎ A．﹣B． C．﹣D．‎ ‎【考点】双曲线的简单性质；余弦定理．‎ ‎【分析】根据题意，当直线MA、MB分别与双曲线相切于点A、B时，可得∠AMB取得最大值．因此设直线AM方程为y=k（x﹣1），与双曲线联解并利用根的判别式，解出k=．设直线AM倾斜角为θ，得∠AMB=2θ且tanθ=，最后利用二倍角的三角函数公式，即可算出∠AMB达到最大值时∠AMB的余弦值．‎ ‎【解答】解：根据题意，当直线MA与双曲线相切于点A，直线MB与双曲线相切于点B时，‎ ‎∠AMB取得最大值．‎ 设直线AM方程为y=k（x﹣1），与双曲线消去y，得 ‎（﹣k2）x2+2k2x﹣k2﹣1=0‎ ‎∵直线MA与双曲线相切于点A，‎ ‎∴（2k2）2﹣4×（﹣k2）×（﹣k2﹣1）=0，解之得k=（舍负）‎ 因此，直线AM方程为y=（x﹣1），‎ 同理直线BM方程为y=﹣（x﹣1），‎ 设直线AM倾斜角为θ，得tanθ=，且∠AMB=2θ ‎∴cos2θ===，即为∠AMB最大时的余弦值 故选：D ‎　‎ ‎12．已知函数f（x）=ex﹣1+x﹣2（e为自然对数的底数），g（x）=x2﹣ax﹣a+3，若存在实数x1，x2，使得f（x1）=g（x2）=0，且|x1﹣x2|≤1，则实数a的取值范围是（　　）‎ A．[2，3]B．[1，2]C．[2，]D．[，3]‎ ‎【考点】函数的值．‎ ‎【分析】求出函数f（x）的导数，可得f（x）递增，解得f（x）=0的解为1，由题意可得x2﹣ax﹣a+3=0在0≤x≤2有解，‎ 即有a==（x+1）+﹣2在0≤x≤2有解，求得（x+1）+﹣2的范围，即可得到a的范围．‎ ‎【解答】解：函数f（x）=ex﹣1+x﹣2的导数为f′（x）=ex﹣1+1＞0，‎ f（x）在R上递增，由f（1）=0，可得f（x1）=0，解得x1=1，‎ 存在实数x1，x2，使得f（x1）=g（x2）=0．且|x1﹣x2|≤1，‎ 即为g（x2）=0且|1﹣x2|≤1，‎ 即x2﹣ax﹣a+3=0在0≤x≤2有解，‎ 即有a==（x+1）+﹣2在0≤x≤2有解，‎ 令t=x+1（1≤t≤3），则t+﹣2在[1，2]递减，[2，3]递增，‎ 可得最小值为2，最大值为3，‎ 则a的取值范围是[2，3]．‎ 故答案为：[2，3]．‎ ‎　‎ 二、填空题 ‎13．某小卖部为了了解热茶销售量y（杯）与气温x（℃）之间的关系，随机统计了某4天卖出的热茶的杯数与当天气温，并制作了对照表：‎ 气温（℃）‎ ‎18‎ ‎13‎ ‎10‎ ‎﹣1‎ 杯数 ‎14‎ ‎24‎ ‎28‎ ‎54‎ 由表中数据算得线性回归方程=bx+a中的b≈﹣2，预测当气温为﹣5℃时，热茶销售量为　60　杯．‎ ‎【考点】线性回归方程．‎ ‎【分析】先计算样本中心点，再求出线性回归方程，进而利用方程进行预测．‎ ‎【解答】解：由题意， ==10， ==30，‎ 将b≈﹣2及（10，30）代入线性回归方程=bx+a，可得a=50，‎ ‎∴x=﹣5时，y=﹣2×（﹣5）+50=60．‎ 故答案为：60．‎ ‎　‎ ‎14．设函数f（x）满足，则f（2）=　　．‎ ‎【考点】函数的值．‎ ‎【分析】通过表达式求出f（），然后求出函数的解析式，即可求解f（2）的值．‎ ‎【解答】解：因为，‎ 所以．‎ ‎，‎ ‎∴．‎ ‎∴=．‎ 故答案为：．‎ ‎　‎ ‎15．在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，三边a、b、c成等差数列，且B=，则（cosA一cosC）2的值为　　．‎ ‎【考点】三角函数的恒等变换及化简求值；等差数列的性质．‎ ‎【分析】由a，b及c成等差数列，利用等差数列的性质列出关系式，将关系式利用正弦定理化简，得到sinA+sinC的值，设cosA﹣cosC=x，根据题意列出关于x的方程，求出方程的解得到x的值，即可求出所求式子的值．‎ ‎【解答】解：∵三边a、b、c成等差数列，且B=，‎ ‎∴2b=a+c，A+C=，‎ 将2b=a+c利用正弦定理化简得：2sinB=sinA+sinC，即sinA+sinC=，‎ 设cosA﹣cosC=x，‎ 可得：（sinA+sinC）2+（cosA﹣cosC）2=2+x2，‎ 即sin2A+2sinAsinC+sin2C+cos2A﹣2cosAcosC+cos2C=2﹣2cos（A+C）=2﹣2cos=2+x2，‎ 则（cosA﹣cosC）2=x2=﹣2cos=．‎ 故答案为：‎ ‎　‎ ‎16．在平面直角坐标系xOy中，已知圆C：x2+（y﹣4）2=4，点A是x轴上的一个动点，直线AP，AQ分别切圆C于P，Q两点，则线段PQ长的取值范围为　[2，4]　．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】设A（a，0），则以AC为直径的圆为x2+y2﹣ax﹣4y=0，与圆C的方程相减，得PQ所在直线的方程为ax﹣4y+12=0，求出圆心C（0，4）到直线：ax﹣4y+12=0的距离d，由|PQ|=2，能求出线段PQ长的取值范围．‎ ‎【解答】解：设A（a，0），则以AC为直径的圆的直径式方程为（x﹣0，y﹣4）•（x﹣a，y﹣0）=0，‎ 即x2+y2﹣ax﹣4y=0，‎ 与圆C的方程x2+（y﹣4）2=4，即x2+y2﹣8y+12=0相减，得ax﹣4y+12=0，‎ ‎∴PQ所在直线的方程为ax﹣4y+12=0，‎ 设圆心C（0，4）到直线：ax﹣4y+12=0的距离为d，‎ 则|PQ|=2=2=2，‎ ‎∴a=0，即A是原点时，|PQ|min=2，‎ 当点A在x轴上无限远时，PQ接近于直径4，‎ ‎∴线段PQ长的取值范围为[2，4）．‎ 故答案为：[2，4）．‎ ‎　‎ 三、解答题 ‎17．已知数列{an}中，a1=1，前n项和Sn=an（n≥2，n∈N*）．‎ ‎（I）求a2，a3及{an}的通项公式；‎ ‎（Ⅱ）记bn=an+，cn=，求数列{cn}的前n项和Tn．‎ ‎【考点】数列的求和；数列递推式．‎ ‎【分析】（I）利用a1=1、Sn=an（n≥2，n∈N*）计算可知a2，a3的值，通过Sn=an（n≥1，n∈N*）与Sn﹣1=an﹣1（n≥2，n∈N*）作差、整理可知=，利用an=••…••a1累乘计算，进而可得结论；‎ ‎（Ⅱ）通过（I）裂项可知cn=﹣，进而并项相加即得结论．‎ ‎【解答】解：（I）∵a1=1，Sn=an（n≥2，n∈N*），‎ ‎∴a1+a2=a2，a2=3a1=3，‎ a1+a2+a3=a3，a3=（a1+a2）=（1+3）=6，‎ ‎∴Sn=an（n≥1，n∈N*），Sn﹣1=an﹣1（n≥2，n∈N*），‎ 两式相减得：an=an﹣an﹣1，‎ 整理得： =，‎ ‎∴an=••…••a1‎ ‎=••…••1‎ ‎=（n≥2，n∈N*），‎ 又∵a1=1满足上式，‎ ‎∴数列{an}的通项公式an=；‎ ‎（Ⅱ）由（I）可知bn=an+=+=，‎ ‎∴cn===﹣，‎ ‎∴Tn=1﹣+﹣+…+﹣‎ ‎=1+﹣﹣‎ ‎=﹣﹣．‎ ‎　‎ ‎18．某单位开展岗前培训．期间，甲、乙2人参加了5次考试，成绩统计如下：‎ 第一次 第二次 第三次 第四次 第五次 甲的成绩 ‎82‎ ‎82‎ ‎79‎ ‎95‎ ‎87‎ 乙的成绩 ‎95‎ ‎75‎ ‎80‎ ‎90‎ ‎85‎ ‎（Ⅰ）根据有关统计知识，回答问题：若从甲、乙2人中选出1人上岗，你认为选谁合适，请说明理由；‎ ‎（Ⅱ）根据有关概率知识，解答以下问题：‎ ‎①从甲、乙2人的成绩中各随机抽取一个，设抽到甲的成绩为x，抽到乙的成绩为y．用A表示满足条件|x﹣y|≤2的事件，求事件A的概率；‎ ‎②若一次考试两人成绩之差的绝对值不超过3分，则称该次考试两人“水平相当”．由上述5次成绩统计，任意抽查两次考试，求至少有一次考试两人“水平相当”的概率．‎ ‎【考点】列举法计算基本事件数及事件发生的概率；众数、中位数、平均数．‎ ‎【分析】（Ⅰ）先求出甲和乙的平均成绩相同，再求出甲和乙的成绩的方差，方差较小的发挥比较稳定，应该派他去．‎ ‎（Ⅱ）①设抽到甲的成绩为x，抽到乙的成绩为y，则所有的（x，y）共有5×5=25个，用列举法求得满足条件|x﹣y|≤2的有5个，由此求得所求事件的概率．‎ ‎②从5此考试的成绩中，任意取出2此，所有的基本事件有 =10个，用列举法求得满足条件至少有一次考试两人“水平相当”的有7个，由此求得所求事件的概率．‎ ‎【解答】解：（Ⅰ）甲的平均成绩为 ==85，乙的平均成绩为==85，‎ 故甲乙二人的平均水平一样．‎ 甲的成绩的方差为 ==31，乙的成绩的方差为 ==50，∴＜，故应派甲合适．‎ ‎（Ⅱ）①从甲、乙2人的成绩中各随机抽取一个，设抽到甲的成绩为x，抽到乙的成绩为y，则所有的（x，y）共有5×5=25个，‎ 其中，满足条件|x﹣y|≤2的有（82，80）、（82，80）、（79，80）、（95，95）、（87，85），共有5个，‎ 故所求事件的概率等于 =．‎ ‎②从5此考试的成绩中，任意取出2此，所有的基本事件有 =10个，‎ 其中，满足至少有一次考试两人“水平相当”的有7个：（79，80）和（87，85）、（79，80）和（82，95）、（79，80）和（87，75）、‎ ‎（79，80）和（95，90）、（87，85）和（82，95）、（87，85）和（82，75）、（87，85）和（95，90），共有7个，‎ 故所求事件的概率等于 ．‎ ‎　‎ ‎19．如图，在四棱锥O﹣ABCD中，底面ABCD是边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点．‎ ‎（Ⅰ）求异面直线AB与MD所成角的大小；‎ ‎（Ⅱ）求点B到平面OCD的距离．‎ ‎【考点】异面直线及其所成的角；点、线、面间的距离计算．‎ ‎【分析】（Ⅰ）求异面直线所成的角，可以做适当的平移，把异面直线转化为相交直线，然后在相关的三角形中借助正弦或余弦定理解出所求的角．平移时主要是根据中位线和中点条件，或者是特殊的四边形，三角形等．∵CD∥AB，∴∠MDC为异面直线AB与MD所成的角（或其补角）．‎ ‎（Ⅱ）在立体几何中，求点到平面的距离是一个常见的题型，同时求直线到平面的距离、平行平面间的距离及多面体的体积也常转化为求点到平面的距离．本题可以先“转化”：当由点向平面引垂线发生困难时，可利用线面平行或面面平行转化为直线上（平面上）其他点到平面的距离．∵AB∥平面OCD，所以点B和点A到平面OCD的距离相等．‎ 连接OP，过点A作AQ⊥OP于点Q．∵AP⊥CD，OA⊥CD，∴CD⊥平面OAP，∴AQ⊥CD．又∵AQ⊥OP，∴AQ⊥平面OCD，线段AQ的长就是点A到平面OCD的距离．‎ ‎【解答】解（Ⅰ）∵CD∥AB，∴∠MDC为异面直线AB与MD所成的角（或其补角）．‎ 作AP⊥CD于点P，连接MP．‎ ‎∵OA⊥平面ABCD，∴CD⊥MP．‎ ‎∵，∴．‎ ‎∵，‎ ‎∴，．‎ 所以，异面直线AB与MD所成的角为．‎ ‎（Ⅱ）∵AB∥平面OCD，所以点B和点A到平面OCD的距离相等．‎ 连接OP，过点A作AQ⊥OP于点Q．‎ ‎∵AP⊥CD，OA⊥CD，∴CD⊥平面OAP，∴AQ⊥CD．‎ 又∵AQ⊥OP，∴AQ⊥平面OCD，线段AQ的长就是点A到平面OCD的距离．‎ ‎∵，，‎ ‎∴．‎ 所以，点B到平面OCD的距离为．‎ ‎　‎ ‎20．已知曲线C1： +=1（a＞b＞0）所围成的封闭图形的面积为4，曲线C1的内切圆半径为，记C2为以曲线C1与坐标轴的交点为顶点的椭圆．‎ ‎（1）求椭圆C2的标准方程；‎ ‎（2）设AB是过椭圆C2中心O的任意弦，M是椭圆上一点，且满足（+）•=0，求△AMB的面积的最小值．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由题意可得，a＞b＞0，解得a，b即可得出．‎ ‎（2）设直线AB的斜率垂直且不为0，方程为y=kx．联立，解得可得|AB|=．由于满足（+）•=0，可得MO⊥AB．可得直线OM的方程为：y=﹣x．同理可得|OM|．利用S△AMB=|OM||AB|及其基本不等式的性质即可得出．当k=0时，S△AMB=．当k不存在时，S△AMB=，直接得出．‎ ‎【解答】解：（1）∵曲线C1： +=1（a＞b＞0）所围成的封闭图形的面积为4，曲线C1的内切圆半径为，‎ ‎∴，a＞b＞0，解得a=，b=2．‎ 由C2为以曲线C1与坐标轴的交点为顶点的椭圆．‎ ‎∴椭圆的标准方程为： +=1．‎ ‎（2）设直线AB的斜率垂直且不为0，方程为y=kx．A（x0，y0），B（﹣x0，﹣y0）．联立，解得x2=，．‎ ‎∴|AB|==．‎ ‎∵满足（+）•=0，∴=0，∴MO⊥AB．可得直线OM的方程为：y=﹣x．‎ 联立，解得x2=，，|MO|==×．‎ ‎∴S△AMB=|OM||AB|=×=20≥20=，当且仅当k2=1时取等号．‎ 当k=0时，S△AMB==2．‎ 当k不存在时，S△AMB==2＞．‎ 综上可得：△AMB的面积的最小值是．‎ ‎　‎ ‎21．已知函数f（x）=ax2﹣lnx．‎ ‎（I）讨论函数f（x）单调性；‎ ‎（Ⅱ）当时，证明：曲线y=f（x）与其在点P（t，f（t））处的切线至少有两个不同的公共点．‎ ‎【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．‎ ‎【分析】（Ⅰ）对原函数求导，然后分a＞0和a≤0两种情况讨论导函数的符号，a≤0时，f′（x）＜0在（0，+∞）恒成立，‎ a＞0时，求导函数的零点，利用导函数的零点把定义域分段，根据导函数在各段内的符号判断原函数在不同区间段内的单调性；‎ ‎（Ⅱ）利用导数求出曲线y=f（x）在点P（t，f（t））处的切线方程，然后构造函数g（x）=f（x）﹣[f′（t）（x﹣t）+f（t）]，因为点P（t，f（t））是曲线y=f（x）与切线的公共点，只要再说明函数g（x）有除了t外的另外零点即可，通过对函数g（x）进行求导，利用函数单调性得到当x∈（0，t）或x∈（t，2]时，g（x）＞g（t）=0，利用放缩法，借助与不等式说明当x＞2t+时，g（x）＜0，从而说明曲线y=f（x）与其在点P（t，f（t））处的切线至少有两个不同的公共点．‎ ‎【解答】（Ⅰ）解：f（x）的定义域为（0，+∞），‎ 由f（x）=ax2﹣lnx，得：f′（x）=2ax﹣．‎ ‎（1）若a≤0，则f′（x）＜0，f（x）在（0，+∞）是减函数；‎ ‎（2）若a＞0，由，得：．‎ 则当x∈（0，）时，f′（x）＜0，f（x）在（0，）是减函数；‎ 当x∈（，+∞）时，f′（x）＞0，f（x）在（，+∞）是增函数．‎ ‎（Ⅱ）证明：曲线y=f（x）在P（t，f（t））处的切线方程为y=f′（t）（x﹣t）+f（t），‎ 且P为它们的一个公共点．‎ 当a=时，，，‎ 设g（x）=f（x）﹣[f′（t）（x﹣t）+f（t）]，则g′（x）=f′（x）﹣f′（t），‎ 则有g（t）=0，且g′（t）=0．‎ 设h（x）=g′（x）=﹣x﹣﹣f′（t），则当x∈（0，2）时，h′（x）=﹣+＞0，‎ 于是g′（x）在（0，2）是增函数，且g′（t）=0，‎ 所以，当x∈（0，t）时，g′（x）＜0，g（x）在（0，t）是减函数；‎ 当x∈（t，2）时，g′（x）＞0，g（x）在（t，2）是增函数．‎ 故当x∈（0，t）或x∈（t，2]时，g（x）＞g（t）=0．‎ 若x∈（2，+∞），则g（x）=﹣x2﹣lnx﹣[f′（t）（x﹣t）+f（t）]‎ ‎=﹣x2+（t+）x﹣t2﹣1﹣ln＜﹣x2+（t+）x﹣t2﹣1=﹣x（x﹣2t﹣）﹣t2﹣1．‎ 当x＞2t+时，g（x）＜﹣t2﹣1＜0．‎ 所以在区间（2，2t+）至少存在一个实数x0＞2，使g（x0）=0．‎ 因此曲线y=f（x）与其在点P（t，f（t））处的切线至少有两个不同的公共点．‎ ‎　‎ ‎[选修4-4：几何证明选讲]‎ ‎22．如图，⊙O是△ABC的外接圆，D是的中点，BD交AC于点E．‎ ‎（1）求证：CD2﹣DE2=AE•EC；‎ ‎（2）若CD的长等于⊙O的半径，求∠ACD的大小．‎ ‎【考点】与圆有关的比例线段；圆內接多边形的性质与判定．‎ ‎【分析】（1）证明△BCD∽△CDE，得出CD2=DE•DB，再利用DE•DB=DE•（DE+BE）即可证明结论成立；‎ ‎（2）连接OC、OD，利用等边△OCD，即可求出∠ACD的大小．‎ ‎【解答】解：（1）证明：∵∠ABD=∠CBD，∠ABD=∠ECD，‎ ‎∴∠CBD=∠ECD，‎ 又∠CDB=∠EDC，‎ ‎∴△BCD∽△CDE，‎ ‎∴=，‎ ‎∴CD2=DE•DB；‎ 又DE•DB═DE•（DE+BE）=DE2+DE•BE，且DE•BE=AE•EC，‎ ‎∴CD2﹣DE2=AE•EC；‎ ‎（2）如图所示，‎ 连接OC、OD，‎ 由题意知△OCD是等边三角形，‎ ‎∴∠COD=60°，‎ ‎∴∠CBD=∠COD=30°，‎ ‎∴∠ACD=∠CBD=30°．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎23．选修4﹣4：坐标系与参数方程．‎ 极坐标系与直角坐标系xoy有相同的长度单位，以原点为极点，以x轴正半轴为极轴，已知曲线C1的极坐标方程为ρ=4cosθ，曲线C2的参数方程为（t为参数，0≤α＜π），射线θ=φ，θ=φ+，θ=φ﹣与曲线C1交于（不包括极点O）三点A、B、C．‎ ‎（I）求证：|OB|+|OC|=|OA|；‎ ‎（Ⅱ）当φ=时，B，C两点在曲线C2上，求m与α的值．‎ ‎【考点】简单曲线的极坐标方程；圆的参数方程．‎ ‎【分析】（Ⅰ）依题意，|OA|=4cosφ，|OB|=4cos（φ+），|OC|=4cos（φ﹣），利用三角恒等变换化简|OB|+|OC|为4cosφ，=|OA|，命题得证．‎ ‎（Ⅱ）当φ=时，B，C两点的极坐标分别为（2，），（2，﹣）．再把它们化为直角坐标，根据C2是经过点（m，0），倾斜角为α的直线，又经过点B，C的直线方程为y=﹣（x﹣2），由此可得m及直线的斜率，从而求得α的值．‎ ‎【解答】解：（Ⅰ）依题意，|OA|=4cosφ，|OB|=4cos（φ+），|OC|=4cos（φ﹣），…‎ 则|OB|+|OC|=4cos（φ+）+4cos（φ﹣）=2（cosφ﹣sinφ）+2（cosφ+sinφ）=4cosφ，‎ ‎=|OA|．…‎ ‎（Ⅱ）当φ=时，B，C两点的极坐标分别为（2，），（2，﹣）．‎ 化为直角坐标为B（1，），C（3，﹣）．…‎ C2是经过点（m，0），倾斜角为α的直线，‎ 又经过点B，C的直线方程为y=﹣（x﹣2），故直线的斜率为﹣，…‎ 所以m=2，α=．…‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．设函数f （x）=|x﹣a|+3x，其中a≠0．‎ ‎（1）当a=2时，求不等式f（x）≥3x+2的解集；‎ ‎（2）若不等式f （x）≤0的解集包含{x|x≤﹣1}，求a的取值范围．‎ ‎【考点】绝对值不等式的解法；集合的包含关系判断及应用．‎ ‎【分析】（1）当a=2时，函数f （x）=|x﹣2|+3x，不等式即|x﹣2|+3x≥3x+2，即|x﹣2|≥2，由此求得它的解集．‎ ‎（2）由不等式可得|x﹣a|≤﹣3x，即，或．分a大于零和a小于零两种情况，分别求得不等式组的解集，再根据f （x）≤0的解集包含{x|x≤﹣1}，求得a的范围．‎ ‎【解答】解：（1）当a=2时，函数f （x）=|x﹣a|+3x=|x﹣2|+3x，‎ 不等式f（x））≥3x+2，即|x﹣2|+3x≥3x+2，即|x﹣2|≥2，‎ ‎∴x﹣2≥2，或 x﹣2≤﹣2．即 x≥4，或 x≤0，故f（x））≥3x+2的解集为{x|x≥4，或 x≤0}．‎ ‎（2）由不等式f （x）≤0，可得|x﹣a|≤﹣3x，即，或．‎ 由于a≠0，‎ ‎①若a＞0，则不等式组的解集为 {x|x≤﹣}．‎ 由f （x）≤0的解集包含{x|x≤﹣1}，可得﹣≥﹣1，求得 0＜a≤2．‎ ‎②若a＜0，则不等式组的解集为 {x|x≤}，‎ 由f （x）≤0的解集包含{x|x≤﹣1}，可得≥﹣1，求得﹣4≤a＜0．‎ 综上可得，a的取值范围为{a|0＜a≤2，或﹣4≤a＜0 }．‎ ‎　‎ ‎2016年7月21日