北京市高考数学联考试题分类大汇编立体几何试题解析 15页

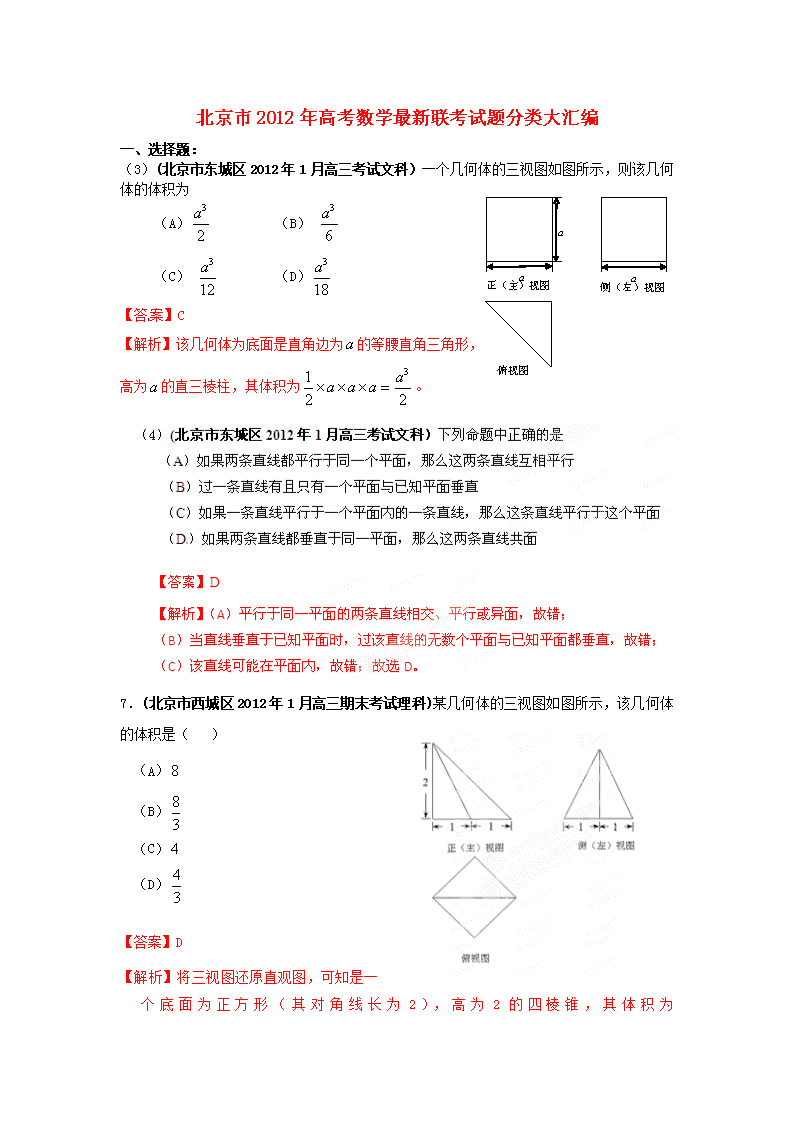
北京市2012年高考数学最新联考试题分类大汇编 一、选择题：‎ ‎ ‎ a ‎ ‎ a ‎ ‎ a ‎ ‎ 正 ‎（‎ 主 ‎）‎ 视图 ‎ ‎ 俯视图 ‎ ‎ 侧 ‎（‎ 左 ‎）‎ 视图 ‎ ‎ ‎（3）(北京市东城区2012年1月高三考试文科）一个几何体的三视图如图所示，则该几何体的体积为 ‎（A） （B） ‎ ‎（C） （D） ‎ ‎【答案】C ‎【解析】该几何体为底面是直角边为的等腰直角三角形，‎ 高为的直三棱柱，其体积为。‎ ‎7．(北京市西城区2012年1月高三期末考试理科)某几何体的三视图如图所示，该几何体的体积是（ ）‎ ‎ （A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎【答案】D ‎【解析】将三视图还原直观图，可知是一个底面为正方形（其对角线长为2），高为2的四棱锥，其体积为 ‎ A．且，则 ‎ ‎ B．且，则 ‎ C．且，则 ‎ ‎ D．且，则 ‎【答案】C体的体积为 . ‎ ‎2‎ ‎1‎ ‎1‎ ‎3‎ ‎3‎ 正视图 侧视图 俯视图 ‎2‎ ‎1‎ ‎（9）(北京市东城区2012年4月高考一模文科)已知一个四棱w ww.ks 5u.c om锥的三视图如图所示，则该四棱锥的体积是 . ‎ ‎10. (2012年4月北京市房山区高三一模理科一个几何体的三视图如图所示，则这个几何体的体积为 . ‎ 三、解答题：‎ ‎（17）(北京市东城区2012年1月高三考试文科）（本小题共14分）‎ 如图，在四棱锥中，底面是正方形，平面， 是中点，为线段上一点.‎ F E D B A P C ‎（Ⅰ）求证：； ‎ ‎（Ⅱ）试确定点在线段上的位置，使//平面，并说明理由.‎ ‎ ‎ ‎ ‎ ‎【命题分析】本题考查线线垂直和线面探索性问题等综合问题。考查学生的空间想象能力。证明线线垂直的方法：（1）异面直线所成的角为直角；（2）线面垂直的性质定理；（3）面面垂直的性质定理；（4）三垂线定理和逆定理；（5）勾股定理；（6）向量垂直.要注意线面、面面垂直的性质定理的成立条件.解题过程中要特别体会平行关系性质的传递性，垂直关系的多样性.本题第一问利用方法二进行证明；探求某证明（Ⅰ）因为平面， ‎ 所以． 又四边形是正方形， ‎ 所以，，‎ 所以平面, 又Ì平面,‎ 所以. ………………7分 ‎ ‎ ‎. ………………14分 ‎(16) （2012年4月北京市海淀区高三一模理科）（本小题满分14分）‎ 在四棱锥中，//，，，平面，. ‎ ‎（Ⅰ）设平面平面，求证：//； ‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）设点为线段上一点，且直线与平面所成角的正弦值为，求的值．‎ ‎(16)（本小题满分14分）‎ ‎………………………………………5分 所以 ，，‎ ‎，‎ 所以，‎ ‎.‎ 所以 ，. ‎ 因为 ，平面，‎ 平面，‎ 所以 平面. ‎ ‎………………………………………9分 由（Ⅱ）知平面的一个法向量为.‎ ‎………………………………………12分 ‎17. (2012年3月北京市朝阳区高三一模文科)（本题满分13分）‎ C A F E B M D 在如图所示的几何体中，四边形为平行四边形，， 平面，，，，，且是的中点.‎ ‎ （Ⅰ）求证：平面；‎ ‎（Ⅱ）在上是否存在一点，使得最大？ ‎ ‎ 若存在，请求出的正切值；若不存在，‎ 请说明理由.‎ ‎（17）（本小题满分13分）‎ ‎ （Ⅱ）解：假设在上存在一点，使得最大.‎ ‎ 因为平面，所以.‎ ‎ 又因为，所以平面. ………………………8分 ‎ 在中，.‎ ‎ 17．(北京市西城区2012年4月高三第一次模拟文)（本小题满分14分）‎ 如图，矩形中，，．，分别在线段和上，∥，将矩形沿折起．记折起后的矩形为，且平面平面．‎ ‎（Ⅰ）求证：∥平面；‎ ‎（Ⅱ）若，求证：； ‎ ‎（Ⅲ）求四面体体积的最大值． ‎ ‎17.（本小题满分14分）‎ ‎（Ⅰ）证明：因为四边形，都是矩形，‎ ‎ 所以 ∥∥，．‎ ‎ 所以 四边形是平行四边形，……………2分 ‎ 所以 ∥， ………………3分 ‎ 因为 平面，‎ 所以 ∥平面． ………………4分 ‎（Ⅱ）证明：连接，设．‎ 因为平面平面，且， ‎ 所以 平面， ……5分 所以 ． …………6分 ‎ ‎9分 ‎ ‎（Ⅲ）解：设，则，其中．‎ 由（Ⅰ）得平面，‎ 所以四面体的体积为． ………11分 所以 ． ……………13分 当且仅当，即时，四面体的体积最大． ………………14分 ‎（17）(北京市东城区2012年4月高考一模理科)（本小题共13分）‎ ‎ ‎ ‎ ‎ 图1 图2 ‎ ‎（17）（共13分）‎ ‎（Ⅰ）证明：取中点，连结.‎ 因为，，‎ 所以，而，即△是正三角形.‎ 又因为, 所以. …………2分 所以在图2中有，.…………3分 所以为二面角的平面角. 图1‎ 又二面角为直二面角，　‎ 所以. …………5分 又因为,　‎ 所以⊥平面,即⊥平面. …………6分 ‎（Ⅱ）解：由（Ⅰ）可知⊥平面，，如图，以 为原点，建立空间直角坐标系，‎ 则，，，.‎ 在图１中，连结.‎ 因为，‎ 所以∥，且.‎ 所以四边形为平行四边形.‎ 所以∥，且.‎ 故点的坐标为（1，，0）. 图2‎ 所以， ，. …………8分 不妨设平面的法向量，则 即令，得.　 …………10分 所以. …………12分 故直线与平面所成角的大小为. …………13分 ‎（17）(北京市东城区2012年4月高考一模文科)（本小题共14分）‎ ‎ 如图，在边长为的正三角形中，，，分别为，，上的点，且满足.将△沿折起到△的位置，使平面平面，连结，.（如图）‎ ‎（Ⅰ）若为中点，求证：∥平面；‎ ‎（Ⅱ）求证：.‎ ‎ ‎ ‎ 图1 图2 ‎ ‎ ‎ ‎（17）（共14分）‎ 证明：（Ⅰ）取中点，连结．‎ ‎ 在△中，分别为的中点，‎ ‎ 所以∥，且． ‎ ‎ 因为，‎ ‎ 所以∥,且，‎ ‎ 所以∥，且． ‎ ‎ 所以四边形为平行四边形．‎ ‎ 所以∥． …………5分 ‎ 又因为平面，且平面，‎ ‎ 所以∥平面． …………7分 ‎（Ⅱ） 取中点，连结.‎ 因为，，‎ 所以，而，即△是正三角形. ‎ 又因为, 所以. ‎ 所以在图2中有. …………9分 因为平面平面，平面平面，‎ 所以⊥平面. …………12分 又平面，‎ 所以⊥. …………14分 ‎17. (2012年3月北京市丰台区高三一模文科)（本小题共14分）‎ 如图，四棱锥P-ABCD中，底面ABCD是菱形，PA=PD，∠BAD=60º，E是AD的中点，点Q在侧棱PC上． ‎ ‎（Ⅰ）求证：AD⊥平面PBE；‎ ‎（Ⅱ）若Q是PC的中点，求证：PA // 平面BDQ；‎ ‎（Ⅲ）若VP-BCDE =2VQ - ABCD，试求的值．‎ ‎17．证明：（Ⅰ）因为 E是AD的中点， PA=PD， ‎ 所以 AD⊥PE． ……………………1分 因为 底面ABCD是菱形，∠BAD=60º，‎ 所以 AB=BD，又因为E是AD的中点，‎ 所以 AD⊥BE． ……………………2分 因为 PE∩BE=E， ……………………3分 所以 AD⊥平面PBE． ……………………4分 ‎（Ⅱ）连接AC交BD于点O，连结OQ．‎ ‎……………………5分 因为O是AC中点， Q是PC的中点，‎ 所以OQ为△PAC中位线．‎ 所以OQ // 因为 ， 所以 ． ……………………14分 ‎17. (2012年4月北京市房山区高三一模理科（本小题共14分）‎ 在直三棱柱中，=2 ,.点分别是 ,的中点，是棱上的动点.‎ ‎（I）求证：平面；‎ ‎(II)若//平面，试确定点的位置，并给出证明；‎ ‎(III)求二面角的余弦值.‎ ‎17．（本小题共14分）‎ ‎(I) 证明：∵在直三棱柱中，，点是的中点，‎ ‎∴ …………………………1分 ‎,, ‎ ‎∴⊥平面 ………………………2分 平面 ‎∴，即 …………………3分 又 ‎∴平面 …………………………………4分 ‎ （II）当是棱的中点时，//平面.……………………………5分 证明如下:‎ 连结,取的中点H，连接, ‎ 则为的中位线 ‎ ‎∴∥，…………………6分 ‎∵由已知条件，为正方形 ‎∴∥，‎ ‎∵为的中点，‎ ‎(III) ∵ 直三棱柱且 又平面的法向量为，‎ ‎==， ……………………13分 设二面角的平面角为，且为锐角 ‎． ……………………14分