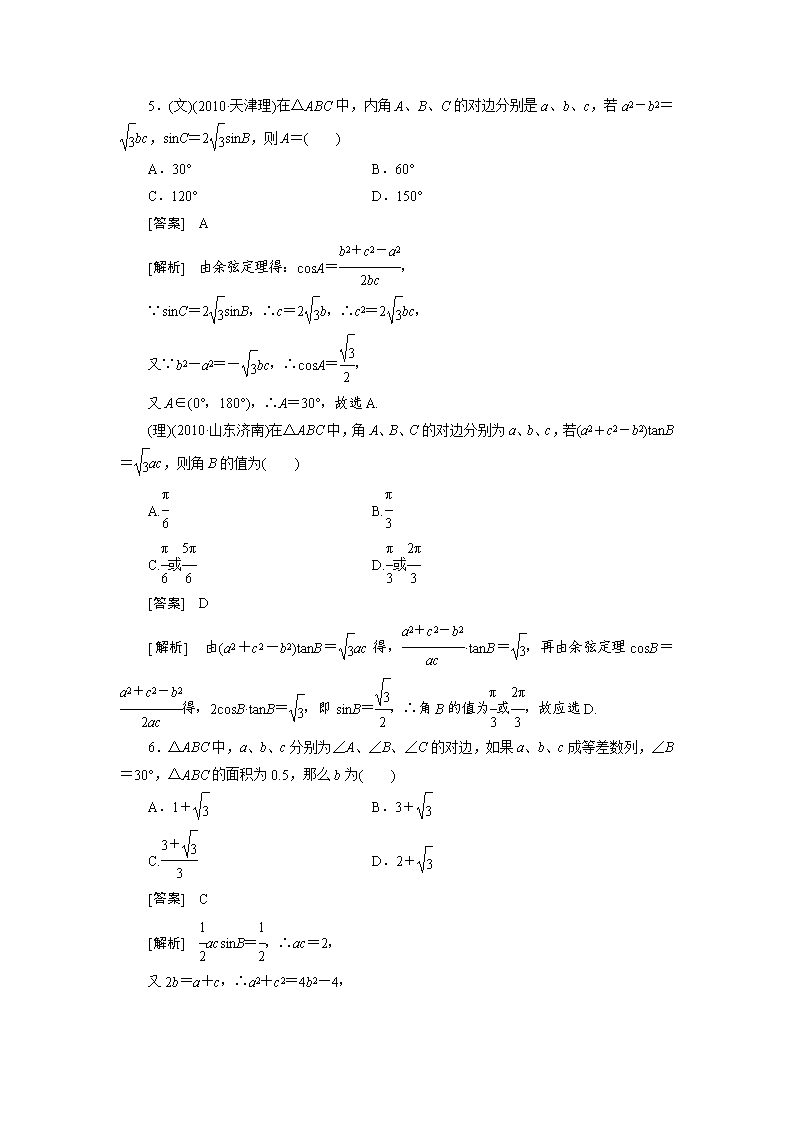1. 您所在位置：首页 > 中小学教育 > 高中教育 > 高考 > 高中数学高考总复习正弦定理与余弦定理习题及详解

高中数学高考总复习正弦定理与余弦定理习题及详解 11页

  • 123.00 KB
  • 2021-05-14 发布

高中数学高考总复习正弦定理与余弦定理习题及详解

  • 11页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
高中数学高考总复习正弦定理与余弦定理习题及详解 一、选择题 ‎1．(2010·聊城市、银川模拟)在△ABC中，a、b、c分别是三内角A、B、C的对边，且sin‎2A－sin‎2C＝(sinA－sinB)sinB，则角C等于(　　)‎ A. B. C. D. ‎[答案]　B ‎[解析]　由正弦定理得a2－c2＝(a－b)·b，‎ 由余弦定理得cosC＝＝，‎ ‎∵00，∴c＝2.故选B.‎ ‎3．在△ABC中，角A、B、C的对边分别是a、b、c，若a＝2，b＝2，且三角形有两解，则角A的取值范围是(　　)‎ A. B. C. D. ‎[答案]　A ‎[解析]　由条件知bsinA0，b>0，∴a－b＝>0，所以a>b.‎ ‎5．(文)(2010·天津理)在△ABC中，内角A、B、C的对边分别是a、b、c，若a2－b2＝bc，sinC＝2sinB，则A＝(　　)‎ A．30° B．60°‎ C．120° D．150°‎ ‎[答案]　A ‎[解析]　由余弦定理得：cosA＝，‎ ‎∵sinC＝2sinB，∴c＝2b，∴c2＝2bc，‎ 又∵b2－a2＝－bc，∴cosA＝，‎ 又A∈(0°，180°)，∴A＝30°，故选A.‎ ‎(理)(2010·山东济南)在△ABC中，角A、B、C的对边分别为a、b、c，若(a2＋c2－b2)tanB＝ac，则角B的值为(　　)‎ A. B. C.或 D.或 ‎[答案]　D ‎[解析]　由(a2＋c2－b2)tanB＝ac得，·tanB＝，再由余弦定理cosB＝得，2cosB·tanB＝，即sinB＝，∴角B的值为或，故应选D.‎ ‎6．△ABC中，a、b、c分别为∠A、∠B、∠C的对边，如果a、b、c成等差数列，∠B＝30°，△ABC的面积为0.5，那么b为(　　)‎ A．1＋ B．3＋ C. D．2＋ ‎[答案]　C ‎[解析]　acsinB＝，∴ac＝2，‎ 又2b＝a＋c，∴a2＋c2＝4b2－4，‎ 由余弦定理b2＝a2＋c2－2accosB得，b＝.‎ ‎7．(2010·厦门市检测)在△ABC中，角A、B、C所对应的边分别为a、b、c，若角A、B、C依次成等差数列，且a＝1，b＝，则S△ABC等于(　　)‎ A. B. C. D．2‎ ‎[答案]　C ‎[解析]　∵A、B、C成等差数列，∴B＝60°，‎ ‎∵＝，∴sinA＝＝＝，‎ ‎∴A＝30°或A＝150°(舍去)，∴C＝90°，‎ ‎∴S△ABC＝ab＝.‎ ‎8．(2010·山师大附中模考)在△ABC中，cos2＝(a、b、c分别为角A、B、C 的对边)，则△ABC的形状为(　　)‎ A．直角三角形 B．正三角形 C．等腰三角形 D．等腰三角形或直角三角形 ‎[答案]　A ‎[解析]　∵cos2＝，∴＝，‎ ‎∴sinCcosB＝sinA，‎ ‎∴sinCcosB＝sin(B＋C)，∴sinBcosC＝0，‎ ‎∵00，cosB>0知A、B均为锐角，‎ ‎∵tanA＝<1，∴0，‎ ‎∴06，无解．‎ ‎④一解，已知两角和一边，三角形唯一确定．‎ ‎(理)在锐角△ABC中，边长a＝1，b＝2，则边长c的取值范围是________．‎ ‎[答案]　0，‎ ‎∴c2<5.∴00，‎ ‎∴c2>3.∴c>.‎ 综上，a＝1，∴l＝a＋b＋c∈(2,3]，‎ 即△ABC的周长l的取值范围为(2,3]．‎ ‎17．(文)△ABC中内角A、B、C的对边分别为a、b、c，向量m＝(2sinB，－)，n＝(cos2B,2cos2－1)且m∥n.‎ ‎(1)求锐角B的大小；‎ ‎(2)如果b＝2，求△ABC的面积S△ABC的最大值．‎ ‎[分析]　(1)问利用平行向量的坐标表示将向量知识转化为三角函数，利用三角恒等变换知识解决；(2)问利用余弦定理与基本不等式结合三角形面积公式解决．‎ ‎[解析]　(1)∵m∥n，‎ ‎∴2sinB＝－cos2B ‎∴sin2B＝－cos2B，即tan2B＝－ 又∵B为锐角，∴2B∈(0，π)，∴2B＝，∴B＝.‎ ‎(2)∵B＝，b＝2，‎ ‎∴由余弦定理cosB＝得，‎ a2＋c2－ac－4＝0‎ 又∵a2＋c2≥‎2ac，∴ac≤4(当且仅当a＝c＝2时等号成立)‎ S△ABC＝acsinB＝ac≤(当且仅当a＝c＝2时等号成立)，‎ ‎[点评]　本题将三角函数、向量与解三角形有机的结合在一起，题目新疑精巧，难度也不大，即符合在知识“交汇点”处构题，又能加强对双基的考查，特别是向量的坐标表示及运算，大大简化了向量的关系的运算，该类问题的解题思路通常是将向量的关系用坐标运算后转化为三角函数问题，然后用三角函数基本公式结合正、余弦定理求解．‎ ‎(理)(2010·山师大附中模考)在△ABC中，角A、B、C的对边分别为a、b、c，已知sinB＝，且a、b、c成等比数列．‎ ‎(1)求＋的值；‎ ‎(2)若accosB＝12，求a＋c的值．‎ ‎[解析]　(1)依题意，b2＝ac 由正弦定理及sinB＝得，sinAsinC＝sin2B＝.‎ ＋＝＋＝＝＝.‎ ‎(2)由accosB＝12知cosB>0，‎ ‎∵sinB＝，∴cosB＝(b不是最大边，舍去负值)‎ 从而，b2＝ac＝＝13.‎ 由余弦定理得，b2＝(a＋c)2－‎2ac－2accosB.‎ ‎∴13＝(a＋c)2－2×13×.‎ 解得：a＋c＝3.‎

您可能关注的文档

相关文档

最近下载