（全国通用）2020版高考物理二轮复习 考前三个月 专题18（选考3-4）教案 20页

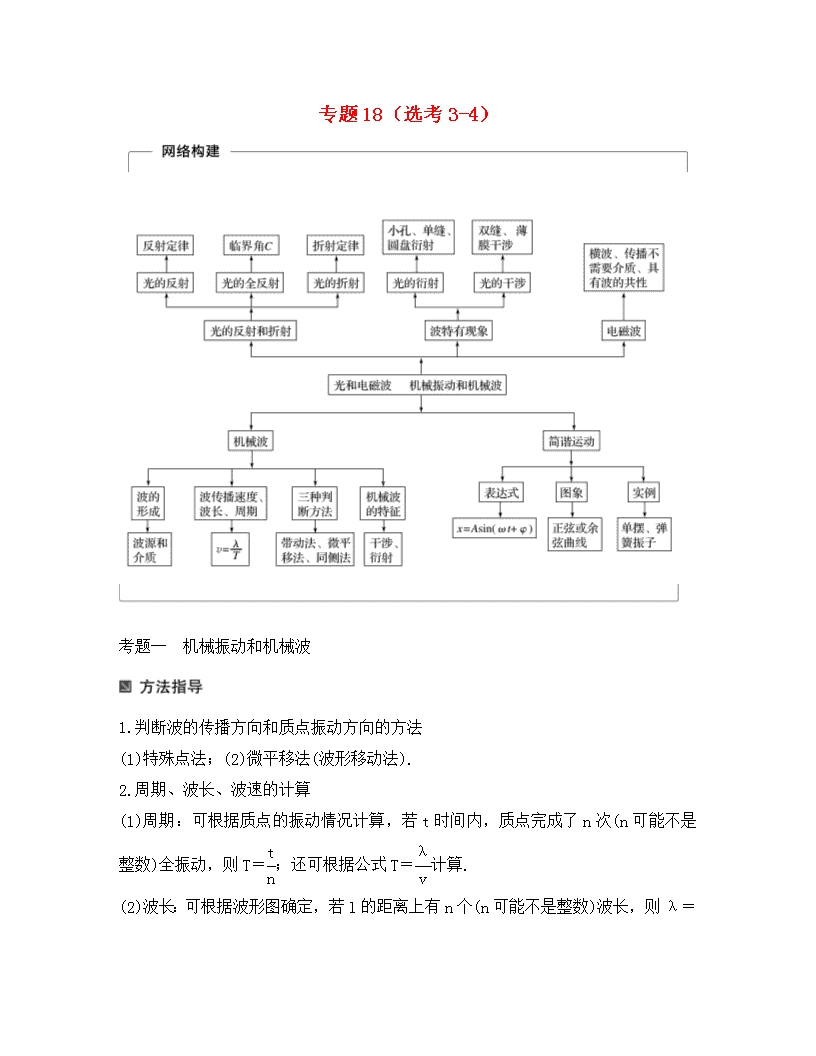
专题18（选考3-4） ‎ 考题一　机械振动和机械波 ‎1.判断波的传播方向和质点振动方向的方法 ‎(1)特殊点法；(2)微平移法(波形移动法).‎ ‎2.周期、波长、波速的计算 ‎(1)周期：可根据质点的振动情况计算，若t时间内，质点完成了n次(n可能不是整数)全振动，则T＝；还可根据公式T＝计算.‎ ‎(2)波长：可根据波形图确定，若l的距离上有n个(n可能不是整数)波长，则λ＝‎ ；也可根据公式λ＝vT计算.‎ ‎(3)波速：可根据波形传播的时间、距离计算v＝；也可根据公式v＝计算.‎ ‎3.利用波传播的周期性、双向性解题 ‎(1)波的图象的周期性：相隔时间为周期整数倍的两个时刻的波形相同，从而使题目的解答出现多解的可能.‎ ‎(2)波传播方向的双向性：在题目未给出波的传播方向时，要考虑到波可沿正向或负向传播的两种可能性.‎ 例1　如图1所示，实线是某时刻的波形图象，虚线是0.2 s后的波形图象，质点P位于实线波的波峰处.‎ 图1‎ ‎(1)若波向右以最小速度传播，求经过t＝4 s质点P所通过的路程；‎ ‎(2)若波速为35 m/s，求波的传播方向.‎ 解析　(1)若波向右传播：‎ nT＋T＝0.2 s(n＝0,1,2,3，…)‎ 由v＝可知周期最大时波速最小，当n＝0时T最大值为 s 经过时间t＝4 s，即经过15个整周期，故质点P通过的路程为s＝15×4A＝1.2 m ‎(2)若波向右传播：nT＋T＝0.2 s(n＝0,1,2,3, …)‎ v＝ 当n＝1时，波速为35 m/s，所以波可以向右传播 若波向左传播：nT＋T＝0.2 s 当n取0或其他任何正整数时，波速都不为35 m/s，所以波不会向左传播.‎ 答案　(1)1.2 m　(2)向右传播 变式训练 ‎1.如图2甲为一列简谐横波在某一时刻的波形图，图乙为介质中x＝2 m处的质点P以此时刻为计时起点的振动图象.下列说法正确的是(　　)‎ 图2‎ A.这列波的传播方向是沿x轴正方向 B.这列波的传播速度是20 m/s C.经过0.15 s，质点P沿x轴的正方向传播了3 m D.经过0.1 s时，质点Q的运动方向沿y轴正方向 E.经过0.35 s时，质点Q距平衡位置的距离小于质点P距平衡位置的距离 答案　ABE 解析　由乙图读出，t＝0时刻质点P的速度向下，由波形的平移法可知，波沿x轴正方向传播，故A正确；由图知：λ＝4 m，T＝0.2 s，则波速v＝＝ m/s＝20 m/s，故B正确；简谐横波中质点在平衡位置附近振动，并不随着波迁移，故C错误；图示时刻Q点沿y轴正方向运动，t＝0.1 s＝T，质点Q的运动方向沿y轴负方向，故D错误；t＝0.35 s＝1.75T，经过0.35 s时，质点P到达波峰，而质点Q位于平衡位置与波谷之间，故质点Q距平衡位置的距离小于质点P距平衡位置的距离，故E正确.故选A、B、E.‎ ‎2.如图3，a、b、c、d是均匀媒质中x轴上的四个质点，相邻两点的间距依次为2 m、4 m和6 m，一列简谐横波以2 m/s的波速沿x轴正向传播，在t＝0时刻到达质点a处，质点a由平衡位置开始竖直向下运动，t＝3‎ ‎ s时a第一次到达最高点.下列说法正确的是(　　)‎ 图3‎ A.在t＝6 s时刻波恰好传到质点d处 B.在t＝5 s时刻质点c恰好到达最高点 C.质点b开始振动后，其振动周期为4 s D.在4 s＜t＜6 s的时间间隔内质点c向上运动 E.当质点d向下运动时，质点b一定向上运动 答案　ACD 解析　ad距离为x＝12 m，则波从a传到d的时间为t＝＝6 s，即在t＝6 s波恰好传到质点d处，故A正确；由题知T＝3 s，得T＝4 s，波从a传到c的时间为t＝＝ s＝3 s，则在t＝5 s质点c已振动了2 s，而c起振方向向下，故在t＝5 s质点c恰好经过平衡位置向上运动，故B错误；质点b的振动周期等于质点a的振动周期，即为4 s，故C正确；在4 s＜t＜6 s的时间间隔内，质点c已振动了1 s，质点c正从波谷向波峰运动，即向上运动，故D正确；波长为λ＝vT＝8 m，bd间距离为10 m＝1λ，结合波形得知，当质点d向下运动时，质点b不一定向上运动，故E错误.‎ ‎3.一列沿x轴正方向传播的简谐横波在t＝0时刻的波形如图4所示，质点P的x坐标为3 m.己知任意振动质点连续2次经过平衡位置的时间间隔为0.4 s.下列说法正确的是(　　)‎ 图4‎ A.波速为1 m/s B.波的频率为1.25 Hz C.x坐标为15 m的质点在t＝0.2 s时恰好位于波峰 D.x坐标为22 m的质点在t＝0.2 s时恰好位于波峰 E.当质点P位于波峰时，x坐标为17 m的质点恰好位于波谷 答案　BDE 解析　由题知，波的周期为T＝2×0.4 s＝0.8 s，由图得波长是 λ＝4 m，则波速v＝＝5 m/s，故A错误；f＝＝ Hz＝1.25 Hz，故B正确；x＝15 m处的质点与P点的振动情况始终相同，P质点经过t＝0.2 s＝T时间恰好经过平衡位置，则x坐标为15 m的质点在t＝0.2 s时恰好位于平衡位置，故C错误；x坐标为22 m的质点到x＝2 m质点的距离为：Δx2＝22 m－2 m＝20 m＝5λ，t＝0时刻x＝2 m的质点向上振动，经过t＝0.2 s＝T时间恰好到达波峰，则x坐标为22 m的质点在t＝0.2 s时恰好位于波峰位置，故D正确；x坐标为17 m的质点到P点的距离为：Δx1＝17 m－3 m＝14 m＝3λ，则x坐标为17 m的质点与P点的振动情况始终相反，当质点P位于波峰时，x坐标为17 m的质点恰好位于波谷，故E正确.故选B、D、E.‎ 考题二　光的折射和全反射 ‎1.在解决光的折射问题时，应先根据题意分析光路，即画出光路图 ，找出入射角和折射角，然后应用公式来求解，找出临界光线往往是解题的关键.‎ ‎2.分析全反射问题时，先确定光是否由光密介质进入光疏介质、入射角是否大于临界角，若不符合全反射的条件，则再由折射定律和反射定律确定光的传播情况.‎ ‎3.在处理光的折射和全反射类型的题目时，根据折射定律及全反射的条件准确作出几何光路图是基础，利用几何关系、折射定律是关键.‎ ‎4.明确两介质折射率的大小关系.‎ ‎(1)若光疏→光密：定有反射、折射光线.‎ ‎(2)若光密→光疏：如果入射角大于或等于临界角，一定发生全反射.‎ 例2　如图5所示，玻璃棱镜ABC可以看成是由ABE、AEC两个直角三棱镜组成的，有关角度如图.一束频率为5.3×1014 Hz的单色细光束从AB面入射，在棱镜中的折射光线如图中ab所示，ab与AB面的夹角α＝60°.已知光在真空中的速度c＝3×108 m/s，玻璃的折射率n ＝1.5.‎ 图5‎ ‎(1)求光在棱镜中的波长；‎ ‎(2)该束光线能否从AC面射出，请通过计算说明.‎ 解析　(1)由n＝，得 v＝＝ m/s＝2×108 m/s 由v＝λf，得λ＝＝ m≈3.77×10－7 m ‎(2)光路如图所示，ab光线在AC面的入射角为45°‎ 设玻璃的临界角为C，则sin C＝＝≈0.67‎ 因sin 45°>0.67，故光线ab在AC面会发生全反射，不能从AC面射出.‎ 答案　(1)3.77×10－7 m　(2)见解析 变式训练 ‎4.一半圆柱形透明物体横截面如图6所示，底面AOB镀银(图中粗线)，O表示半圆截面的圆心.一束光线在横截面内从M点的入射角为30°，∠MOA＝60°，∠NOB＝30°.(已知sin 15°＝)求：‎ 图6‎ ‎(1)光线在M点的折射角；‎ ‎(2)透明物体的折射率.‎ 答案　(1)15°　(2) 解析　(1)如图，透明物体内部的光路为折线MPN，Q、M点相对于底面EF对称，Q、P和N三点共线.设在M点处，光的入射角为i，折射角为r，∠OMQ＝α，∠PNF＝β.根据题意有 α＝30°‎ 由几何关系得，∠PNO＝∠PQO＝r，则有：β＋r＝60°‎ 且α＋r＝β 联立式得： r＝15°‎ ‎(2)根据折射率公式有 sin i＝nsin r 得n＝.‎ ‎5.如图7所示，AOB是截面为圆形、半径为R的玻璃砖，现让一束单色光在横截面内从O A靠近O点处平行OB射入玻璃砖，光线可从OB面射出；保持光束平行OB不变，逐渐增大入射点与O的距离，当入射点到达OA的中点E时，一部分光线经AB面反射后恰好未从OB面射出.不考虑多次反射，求玻璃的折射率n及OB上有光射出的范围.‎ 图7‎ 答案　2　R 解析　设光线经E点射到AB面时入射角为α，因E点为OA的中点 由几何知识可知入射角：α＝30°‎ 设临界角为C，则有C＝30°‎ 因恰好发生全反射，则：sin C＝ 解得：n＝2‎ 由题意可知，光从OE间入射时，可从OB上射出，则从E点入射时出射点距O最远，设为F，则：‎ OF＝ 得OF＝R.‎ ‎6.如图8所示为一顶角θ＝90°的三棱镜截面，一束单色光从三棱镜AB边上的D点入射，若入射角由0逐渐增大，发现光线均能射到AC边，但当入射角大于45°时，在AC边左侧无光线射出(不考虑光线在BC、AC边的反射).求三棱镜的折射率.‎ 图8‎ 答案　 解析　如图，入射光线经AB边D点折射进入三棱镜，折射角为γ，当入射角α＝45°时，折射光线射到AC边恰好发生全反射，在AC边左侧无光线射出，‎ 则由折射定律可得：n＝ 由临界角定义可得：sin C＝ 由几何关系得C＋γ＝θ 联立解得：n＝.‎ 考题三　光的几种特性 ‎1.光的干涉现象和衍射现象证明了光的波动性，光的偏振现象说明光波为横波.相邻两亮条纹(或暗条纹)间的距离与波长成正比，即Δx＝λ，利用双缝干涉实验可测量光的波长.‎ ‎2.干涉和衍射的产生条件 ‎(1)双缝干涉产生亮、暗条纹的条件：屏上某点到双缝的光程差等于波长的整数倍时，该点干涉加强，出现亮条纹；当光程差等于半波长的奇数倍时，该点干涉减弱，出现暗条纹.‎ ‎(2)发生明显衍射的条件：障碍物或小孔的尺寸跟光的波长相差不多或比光的波长小.‎ 例3　2020年，科学家利用激光干涉方法探测到由于引力波引起的干涉条纹的变化，这是引力波存在的直接证据.关于激光，下列说法中正确的是(　　)‎ A.激光是自然界中某种物质直接发光产生的，不是偏振光 B.激光相干性好，任何两束激光都能发生干涉 C.用激光照射不透明挡板上小圆孔时，光屏上能观测到等间距的光环 D.激光全息照片是利用光的干涉记录下物体三维图象的信息 答案　D 解析　激光是人造光，也是偏振光，故A错误；激光相干性好，只有频率相同的两束激光才会发生干涉，故B错误；用激光照射不透明挡板上小圆孔时，光屏上能观测到衍射条纹，间距不等，故C错误；激光全息照片是利用光的干涉记录下物体三维图象的信息，故D正确.故选D.‎ 变式训练 ‎7.如图9所示，光源S从水面下向真空斜射一束由红光和蓝光组成的复色光，在A点分成a、b两束，则下列说法正确的是(　　)‎ 图9‎ A.a光是蓝光 B.射出水面前a光的传播速度大，射出水面后二者传播速度一样大 C.逐渐增大入射角，a光最先发生全反射 D.b光比a光更容易发生衍射现象 答案　B 解析　由图知，两光束的入射角i相同，折射角的关系为 ra＜rb，根据折射定律n＝得：折射率关系为 na＜nb，由于蓝光的折射率比红光的大.则知a光是红光，b光是蓝光，故A错误；射出水面前a光的传播速度大，射出水面后，所有色光在真空传播速度都相同，都为c＝3×108 m/s，故B正确；a光的折射率小，根据临界角公式sin C＝ ‎，可知，b光的临界角较小，则逐渐增大入射角时，b光的入射光先达到其临界角，最先发生全反射，故C错误；b光的折射率比a光的大，则b光的频率比a光的大，波长比a光的小，则a光比b光更容易发生衍射现象，故D错误.故选B.‎ ‎8.如图10所示，实线表示两个相干波源S1、S2发出的波的波峰位置，设波的周期为T，波长为λ，波的传播速度为v，下列说法正确的是(　　)‎ 图10‎ A.图中的a点为振动减弱点的位置 B.图中的b点为振动加强点的位置 C.v＝λT D.波源S1的波经过干涉之后波的性质完全改变 E.从图中时刻开始，波源S1的波峰传播到a、b位置的最短时间均为 答案　ABE 解析　由图知，a点到波源S1、S2的距离为2.5λ和4λ，路程差为Δs＝1.5λ，则a点为振动减弱的位置，故A正确；b点到波源S1、S2的距离都是3.5λ，路程差为Δs＝0，则b点为振动加强的位置，故B正确；v＝，故C错误；频率相同时，才能发生干涉，而干涉为波的叠加，不会改变波的性质，故D错误；由T＝，对波源S1，a、b两点均处于波谷位置，故波源S1的波峰传播到a、b位置的最短时间均为T，故E正确.故选A、B、E.‎ ‎9.如图11所示，实线为空气和水的分界面，一束绿光从水中的A点沿AO1方向(O1点在分界面上，图中O1点和入射光线都未画出)射向空气，折射后通过空气中的B点，图中O点为A、B连线与分界面的交点.下列说法正确的是(　　)‎ 图11‎ A.O1点在O点的右侧 B.绿光从水中射入空气中时，速度变大 C.若增大入射角，可能在空气中的任何位置都看不到此绿光 D.若沿AO1方向射向空气的是一束蓝光，则折射光线有可能通过B点正上方的C点 E.若沿AO1方向射向空气的是一束红光，则折射光线有可能通过B点正上方的C点 答案　BCE 解析　光由水射入空气中折射时折射角大于入射角，画出绿光的光路图如图所示，可见O1点在O点的左侧，故A错误；光在真空中速度最大，当绿光从水中射入空气中时，速度变大，故B正确；光由水中射入空气时，入射角增大到一定的值会发生全反射，则可能在空气中的任何位置都看不到绿光，故C正确；若沿AO1方向射向空气中的是一束蓝光，水对蓝光的折射率大于绿光的折射率，根据折射定律可知，蓝光的偏折程度大于绿光的偏折程度，所以折射光线不可能通过B点正上方的C点，故D错误；若沿AO1方向射向空气中的是一束红光，水对红光的折射率小于绿光的折射率，根据折射定律可知，红光的偏折程度小于绿光的偏折程度，所以折射光线有可能通过B点正上方的C点，故E正确.故选B、C、E.‎ 专题规范练 ‎1.(1)沿x轴正方向传播的一列简谐横波在t＝0时刻的波形如图1所示，M为介质中的一个质点，该波的传播速度为40 m/s，则下列说法正确的是(　　)‎ 图1‎ A.t＝0.05 s时质点M相对平衡位置的位移一定为负值 B.t＝0.05 s时质点M的速度方向与相对平衡位置的位移方向相反 C.t＝0.025 s时质点M的加速度方向与速度方向一定相同 D.t＝0.025 s时质点M的加速度方向与相对平衡位置的位移方向相同 E.质点M在0.05 s内通过的路程一定等于4 cm ‎(2)半径为R的固定半圆形玻璃砖的横截面如图2所示，O点为圆心，OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ＝30°角射向O点，已知复色光包含有折射率从n1＝到n2＝的光束，因而光屏上出现了彩色光带.‎ 图2‎ ‎①求彩色光带的宽度；‎ ‎②当复色光入射角逐渐增大时，光屏上的彩色光带将变成一个光点，求此时θ的大小.‎ 答案　(1)ACE　(2)①(1－)R　②45°‎ 解析　(1)从波的图象可以看出波长为λ＝4 m，则周期为T＝＝ s＝0.1 s；因为波沿x轴正方向传播，故质点M向上振动，经过0.05 s即半个周期，对平衡位置的位移为负，‎ ‎ 故A正确；经过半个周期，速度方向也为负，与位移方向相同，故B错误；经过0.025 s，质点M沿y轴负方向振动，但还没有到达平衡位置，故加速度方向也为负，故C正确；加速度方向与位移方向总是反向，故D错误；半个周期内质点通过的路程总是振幅的2倍，故E正确.故选A、C、E.‎ ‎(2)①由折射定律有n1＝ n2＝ 代入数据解得：β1＝45°　β2＝60°‎ 故彩色光带的宽度为：Rtan 45°－Rtan 30°＝(1－)R ‎②此时折射率为n1的单色光恰好发生全反射，故sin C＝＝ 即入射角θ＝C＝45°‎ ‎2.(1)两列简谐横波Ⅰ和Ⅱ分别沿x轴正方向和负方向传播，两列波的波速大小相等，振幅均为5 cm.t＝0时刻两列波的图象如图3所示，x＝－1 cm和x＝1 cm的质点刚开始振动.以下判断正确的是(　　)‎ 图3‎ A.Ⅰ、Ⅱ两列波的频率之比为2∶1‎ B. t＝0时刻，P、Q两质点振动的方向相同 C.两列波将同时传到坐标原点O D.两列波的波源开始振动的起振方向相同 E.坐标原点始终是振动加强点，振幅为10 cm ‎(2)如图4所示，将半径为R的透明半球体放在水平桌面上方，O为球心，直径恰好水平，轴线OO′垂直于水平桌面.位于O点正上方某一高度处的点光源S发出一束与OO′的夹角θ＝60°的单色光射向半球体上的A点，光线通过半球体后刚好垂直射到桌面上的B点，已知O′B＝R，光在真空中传播速度为c，不考虑半球体内光的反射，求：‎ 图4‎ ‎①透明半球体对该单色光的折射率n；‎ ‎②该光在半球体内传播的时间t.‎ 答案　(1)ACD　(2)①　② 解析　(1)由图知Ⅰ、Ⅱ两列波的波长之比为1∶2，波速相等，由v＝λf可知，Ⅰ、Ⅱ两列波的频率之比为2∶1，故A正确；由“上、下坡法”知，t＝0时Q向上振动，P向下振动，故B错误；两列波到O点的距离相同，波速相同，故同时传到O点，故C正确；由图可知，两列波的起振方向都向上，故D正确；由图可知，坐标原点并非始终是振动加强点，故E错误.故选A、C、D.‎ ‎(2)①光从光源S射出经半球体到达水平桌面的光路如图所示：‎ 光由空气射向半球体，由折射定律，有：n＝ 在△OCD中，sin ∠COD＝得：γ＝∠COD＝60°‎ 光由半球体射向空气，由折射定律，有：n＝ 则α＝β，由几何知识α＋β＝60°‎ 得：α＝β＝30°‎ 则n＝＝ ‎②光在半球体中传播的速度为：v＝＝c 由几何知识得 2ACcos 30°＝R，得：AC＝R 光在半球体中传播的时间为：t＝＝.‎ ‎3.(1)图5(a)为一列简谐横波在t＝2 s时刻的波形图，图(b)为介质中平衡位置在x＝1.5 m处的振动图象，P是平衡位置为x＝2 m处的质点，下列说法正确的是(　　)‎ 图5‎ A.波的传播方向向右 B.波速为0.5 m/s C.0～2 s时间内，P运动的路程为8 cm D.0～2 s时间内，P向y轴正方向运动 E.当t＝7 s时，P点恰好回到平衡位置 ‎(2)单色细光束射到折射率n＝的透明球面，光束在过球心的平面内，入射角i＝45°，研究经折射进入球内后，又经内表面反射一次，再经球面折射后射出的光线，如图6所示(图上已画出入射光和出射光).‎ 图6‎ ‎①在图上大致画出光线在球内的路径和方向；‎ ‎②求入射光与出射光之间的夹角α.‎ 答案　(1)BCE　(2)①见解析图　②30°‎ 解析　(1)由图(b)知，x＝1.5 m处的质点在t＝2 s时振动方向向下，则该波向左传播，故A错误；由图(a)可知波长为2 m，由图(b)知周期为4 s，则波速为v＝＝0.5 m/s，故B正确；在t＝2 s时，质点P在波谷，且2 s＝0.5T，则质点P运动的路程为2A＝8 cm，故C正确；因波向左传播，由图(a)知在t＝2 s时，质点P已经在波谷，则0～2 s时间内，P向y轴负方向运动，故D错误；当t＝7 s时，Δt＝5 s＝1T，P恰好回平衡位置，故E正确.故选B、C、E.‎ ‎(2)①光线从入射到出射的光路如图所示 ‎②由折射定律n＝得sin r＝＝＝ 所以r＝30°‎ 由几何关系及对称性得：＝r－(i－r)＝2r－i 所以α＝4r－2i，把r＝30°，i＝45°代入得：α＝30°‎ ‎4.(1)如图7所示，横截面为半圆形玻璃砖，O点为圆心，OO′为直径PQ的垂线.已知玻璃砖的折射率n＝，光在真空中的速度为c.则光线在该玻璃砖中的传播速度为________；一条与OO′连线成60°角的光线从玻璃砖的圆心射入玻璃砖，则光线从玻璃砖出射方向与最初入射方向的夹角为________.‎ 图7‎ ‎(2)如图8所示为一列简谐横波沿－x方向传播在t＝0时刻的波形图，M、N两点的坐标分别为(－2,0)和(－7,0)，已知t＝0.5 s时，M点第二次出现波峰.‎ 图8‎ ‎①这列波的传播速度多大？‎ ‎②从t＝0时刻起，经过多长时间N点第一次出现波峰？‎ ‎③当N点第一次出现波峰时，M点通过的路程为多少？‎ 答案　(1)c　30°　(2)①20 m/s　②0.55 s　③0.4 m 解析　(1)光线在玻璃砖中传播的速度为：v＝＝c.根据折射定律得：n＝得：r＝30°，光线沿半径方向射向界面，则沿半径方向射出，可知光线从玻璃砖出射方向与最初入射方向的夹角为30°.‎ ‎(2)①由图象知，波长 λ＝4 m，M点与最近波峰的水平距离为6 m，距离下一个波峰的水平距离为s0＝10 m，则波速为：v＝＝20 m/s ‎②N点与最近波峰的水平距离为s＝11 m，当最近的波峰传到N点时N点第一次形成波峰，历时为：t1＝＝ s＝0.55 s ‎③该波中各质点振动的周期为：T＝＝0.2 s，N点第一出现波峰时质点M振动了 t2＝‎ s＝0.4 s 则 t2＝2T，质点M每振动经过的路程为5 cm，则当N点第一次出现波峰时，M点通过的路程为：s′＝8×5 cm＝40 cm＝0.4 m.‎ ‎5.(1)下列说法正确的是(　　)‎ A.光导纤维传输信号是利用光的干涉现象 B.全息照相利用了激光相干性好的特性 C.光的偏振现象说明光是横波 D.X射线比无线电波更容易发生干涉和衍射现象 E.刮胡须的刀片的影子边缘模糊不清是光的衍射现象 ‎(2)如图9a所示，用一根不可伸长的轻质细线将小球悬挂于天花板上的O点，现将小球拉离平衡位置，使细线与竖直方向成一夹角(小于5°)后由静止释放.小球的大小和受到的空气阻力均忽略不计.‎ 图9‎ ‎①证明小球的运动是简谐运动；‎ ‎②由传感器测得小球偏离平衡位置的位移随时间变化的规律如图b所示，求小球运动过程中的最大速度值.‎ 答案　(1)BCE　(2)①见解析　②0.08π m/s 解析　(1)光导纤维传输信号是利用光的全反射现象，故A错误；全息照相利用了激光相干性好的特性，故B正确；光的偏振现象说明光是横波，故C正确；X射线比无线电波的波长短，则衍射现象不明显，故D错误；刮胡须的刀片的影子边缘模糊不清是光的衍射现象，故E正确.故选B、C、E.‎ ‎(2)①证明：设摆长为l，小球离开平衡位置的位移为x时，细线和竖直方向夹角为θ ，小球重力的分力F1提供回复力，其大小 F1＝mgsin θ 在偏角很小时sin θ≈ 单摆的回复力与位移的关系 F回＝－x 所以小球的运动是简谐运动 ‎②根据图b可得小球偏离平衡位置的位移随时间变化的关系式x＝0.08sin πt (m)‎ 所以小球的速度随时间变化的规律为 v＝0.08πcos πt (m/s)‎ 则小球的最大速度 vm＝0.08π m/s.‎