全国高考数学试题全国理 16页

‎2000年普通高等学校招生全国统一考试 数学（理工农医类）‎ ‎　‎ ‎　　本试卷分第I卷（选择题）和第II卷（非选择题）两部分。第I卷1至2页。第II卷3至9页。共150分。考试时间120分钟。‎ 第I卷（选择题60分）‎ ‎　　注意事项： 　　1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。 　　2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答，不能答在试题卷上。 　　3．考试结束，监考人将本试卷和答题卡一并收回。 　　参考公式： 　　三角函数的积化和差公式　　　　　　　正棱台、圆台的侧面积公式 　　　　　 　　　　　 其中c′、c分别表示上、下底面周长，l表示斜高或母线长 　　　　　 　　 　　 其中S′、S分别表示上、下底面积，h表示高 ‎　　一、选择题：本大题共12分，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。 　　（1）设集合A和B都是自然数集合N，映射f：A→B把集合A中的元素n映射到集合B中的元素，则在映射f下，象20的原象是（ ） 　　（A）2 　　　　　（B）3　　　　　 （C）4　　　　　　　 （D）5 ‎ ‎　　（2）在复平面内，把复数对应的向量按顺时针方向旋转，所得向量对应的复数是 　　（A）　　　　（B）　　　 （C）　　　　　（D） 　　（3）一个长方体共一顶点的三个面的面积分别是，这个长方体对角线的长是 　　（A）　　　　（B）　　　　 （C）6　　　　　　　 （D） 　　（4）已知sinα>sinβ，那么下列命题成立的是 　　（A）若α、β是第一象限角，则cosα>cosβ 　　（B）若α、β是第二象限角，则tgα>tgβ 　　（C）若α、β是第三象限角，则cosα>cosβ 　　（D）若α、β是第四象限角，则tgα>tgβ 　　（５）函数y=-xcosx的部分图象是 　　　　　　 　　（６）《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分希累进计算。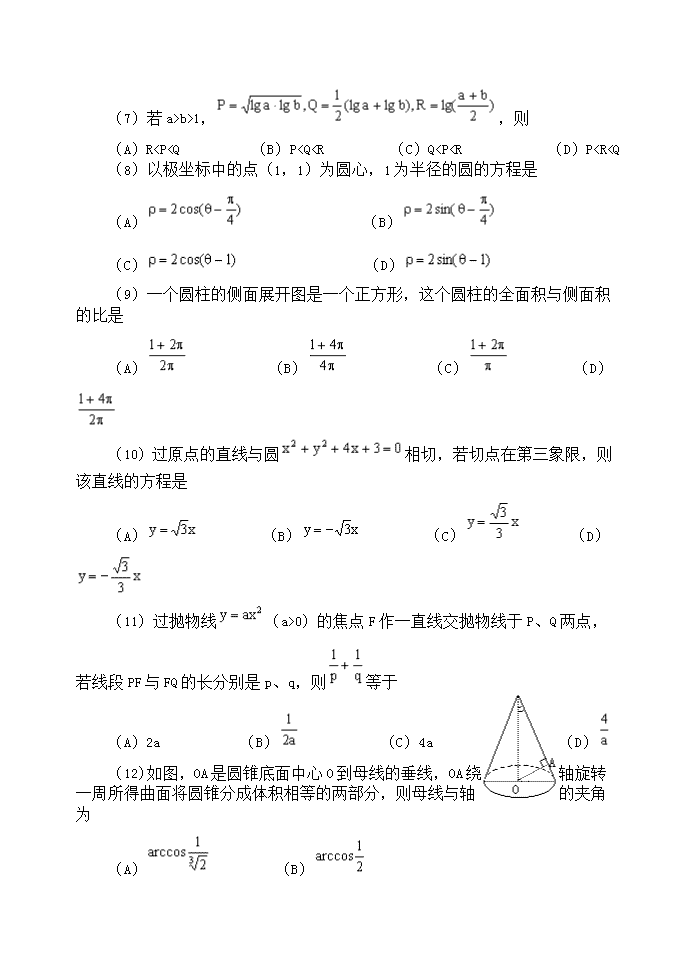‎ ‎　　　　　 全月应纳税所得额税率 ‎ 不超过500元的部分5%‎ 超过500元至2000元的部分 10% ‎ 超过2000元至5000元的部分 15% ‎ ‎… … ‎ 某人一月份应交纳此项税款26.78元，则他的当月工资、薪金所得介于 　　（A）800～900元（B）900～1200元　（C）1200～1500元（D）1500～2800元 ‎ ‎　　（7）若a>b>1，，则 　　（A）R0）的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是p、q，则等于 　　（A）2a　　　　　（B）　　　　　（C）4a　　　　　（D） 　　（12）如图，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为 　　（A）　　　　（B）　　　‎ ‎（C）　　　　（D）‎ ‎2000年普通高等学校招生全国统一考试 数　学（理工农医类） 第II卷（非选择题共90分）‎ ‎　　注意事项： 　　1．第II卷共7页，用钢笔或圆珠笔直接答在试题卷中。 　　2．答卷前将密封线内的项目填写清楚。‎ ‎　‎ 二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。 　　（13）乒乓球队的10名队员中有3名主力队员，派5名参加比赛，3名主力队员要安排在第一、第三、五位置，其余7名队员选2名安排在第二、四位置，那么不同的出场安排共有_________种（用数字作答） 　　（14）椭圆的焦点为，点P为其上的动点。当为钝角时，点P横坐标的取值范围是__________________。 　　（15）设是首项为1的正项数列，且（n=1，2，3…），则它的通项公式是=_________。 　　（16）如图，E、F分别为正方体的面、面的中心，则四边形在该正方体的面上的射影可能是__________________。 　　　　　　 　　（要求：把可能的图的序号填上） 　　三、解答题：本大题共16小题，共74分，解答应写出文字说明，证明过程或演算步骤。 ‎ ‎　　17（本小题满分12分） 　　已知函数 　　（I）当函数y取得最大值时，求自变量x的集合； 　　（II）该函数的图象可由y=sinx（x∈R）的图象经过怎样的平移和伸缩变换得到？ 　　（18）（本小题满分12分） 　　如图，已知平行六面体的底面ABCD是菱形，且 　　（I）证明：； 　　（II）假定CD=2，，记面为α，面CBD为β，求二面角α BD β的平面角的余弦值； 　　（III）当的值为多少时，能使？请给出证明。 　　（19）（本小题满分12分） 　　设函数，其中a>0。 　　（I）解不等式f(x)≤1； 　　（II）求a的取值范围，使函数f(x)在区间[0，+∞)上是单调函数。 　　（20）（本小题满分12分） 　　（I）已知数列，其中，且数列为等比数列，求常数p； 　　（II）设是公比不相等的两个等比数列，，证明数列不是等比数列。 　　（21）（本小题满分12分） 　　某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线段表示。 　　（I）写出图一表示的市场售价与时间的函数关系P=f(t)； ‎ ‎　　写出图二表求援 种植成本与时间的函数关系式Q=g(t)； 　　（II）认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？ 　　　　　　　　 　　（注：市场售价和种植成本的单位：，时间单位：天） 　　（22）（本小题满分14分） 　　如图，已知梯形ABCD中|AB|=2|CD|，点E分有向线段所成的比为λ，双曲线过C、D、E三点，且以A、B为焦点。当时，求双曲线离心率e的取值范围。 　　‎ ‎ 　　‎ ‎2000年普通高等学校招生全国统一考试 ‎ 数学试题（理工农医类）参考解答及评分标准 ‎　‎ ‎　　说明： 　　一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则。 ‎ ‎　　二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分。 　　三、解答右端所注分数，表示考生正确做到这一步应得的累加分数。 　　四、只给整数分数，选择题和填空题不给中间分。‎ ‎　　一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分。 　　（1）C　　（2）B　　（3）D　　（4）D　　（5）D　　（6）C 　　（7）B　　（8）C　　（9）A　　（10）C　 （11）C　 （12）D 　　二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分。 　　（13）252 　　（14）　　　（15）　　　（16）②③ 　　三、解答题 　　（17）本小题主要考查三角函数的图象和性质，考查利用三角公式进行恒等变形的技能以及运算能力。满分12分。 　　解：（I） 　　　　　　　 　　　…………6分 　　y取得最大值必须且只需 　　 　　即 　　所以当函数y取得最大值时，自变量x的集合为 　　　　　　　　　　　　　　　　　　　　　　　　　　　…………8分 ‎ ‎　　（II）将函数y=sinx依次进行如下变换： 　　（i）把函数y=sinx的图象向左平移，得到函数的图象； 　　（ii）把得到的图象上各点横坐标缩短到原来的倍（纵坐标不变），得到函数的图象； 　　（iii）把得到的图象上各点纵坐标缩短到原来的倍（横坐标不变），得到函数的图象； 　　（iv）把得到的图象向上平移个单位长度，得到函数的图象； 　　综上得到函数的图象。　　　　　　　　　　　………………12分 　　（18）本小题主要考查直线与直线、直线与平面的关系，逻辑推理能力，满分12分。 　　（I）证明：连结、AC，AC和BD交于O，连结 　　∵四边形ABCD是菱形 　　∴AC⊥BD，BC=CD 　　又 　　 　　 ‎ ‎　　∵DO=OB 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　………………2分 　　但AC⊥BD， 　　 　　又 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　………………4分 　　（II）解：由（I）知AC⊥BD， 　　是二面角α BD β的平面角 　　在中，BC=2，， 　　　　　　　　　　　　　　　　　………………6分 　　∵∠OCB=60° 　　 　　 　　 　　作，垂足为H。 　　∴点H是OC的中点，且， ‎ ‎　　所以。　　　　　　　　　　　　　　　　　　　　………………8分 　　（III）当时，能使 　　证明一： 　　∵ 　　 　　又 　　由此可推得 　　∴三棱锥是正三棱锥。　　　　　　　　　　　　　　　　　　　………………10分 　　设相交于G. 　　 　　 　　又是正三角形的BD边上的高和中线, 　　∴点G是正三角形的中心。 　　 　　即。　　　　　　　　　　　　　　　　　　　　　　　　………………12分 　　证明二： ‎ ‎　　由（I知， 　　。　　　　　　　　　　　　　　　　　　　　………………10分 　　当时，平行六面体的六个面是全等的菱形。 　　同的证法可得 　　又 　　　　　　　　　　　　　　　　　　　　　　　　　　　………………12分 　　（19）本小题主要考查不等式的解法、函数的单调性等基本知识，分数计论的数学思想方法和运算、推理能力。满分12分。 　　解：（I）不等式f(x)≤1即 　　， 　　由此得1≤1+ax，即ax≥0，其中常数a>0 　　所以，原不等式等价于 　　 　　即　　　　　　　　　　　　　　　　　　　　　　　　　………………3分 　　所以，当087.5可知，h(t)在区间[0，300]上可以取得最大值100，此时t=50，即从二月一日开始的第50天时，上市的西红柿纯收益最大。　　　　　　　　　　　　　　　　　　　……………………12分 　　（22）本小题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质，推理、运算能力和综合应用数学知识解决问题的能力，满分14分。 　　解：如图，以AB的垂直平分线为y轴，直线AB为x轴，建立直角坐标系xOy，则CD⊥y轴。 　　因为双曲线经过点C、D，且以A、B为焦点，由双曲线的对称性知C、D关于x轴对称。 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　………………2分 　　依题意，记A（-c，0），，其中为双曲线的半焦距，h是梯形的高。 　　由定比分点坐标公式得 ‎ ‎　　 　　。 　　设双曲线的方程为，则离心率。 　　由点C、E在双曲线上，将点C、E的坐标和代入双曲线方程得 　　　　　　　　　　　 ① 　　 　　 ②　　　　　　　　　　　　　　　　……………………7分 　　由①式得 ③ 　　将③式代入②式，整理得 　　 　　故。　　　　　　　　　　　　　　　　　　　　　　　　……………………10分 　　由题设得， 　　解得 　　所以双曲线的离心率的取值范围为。　　　　　　　　　　　……………………14分 　　‎