- 315.00 KB
- 2021-05-14 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
4. 平面向量 知识要点
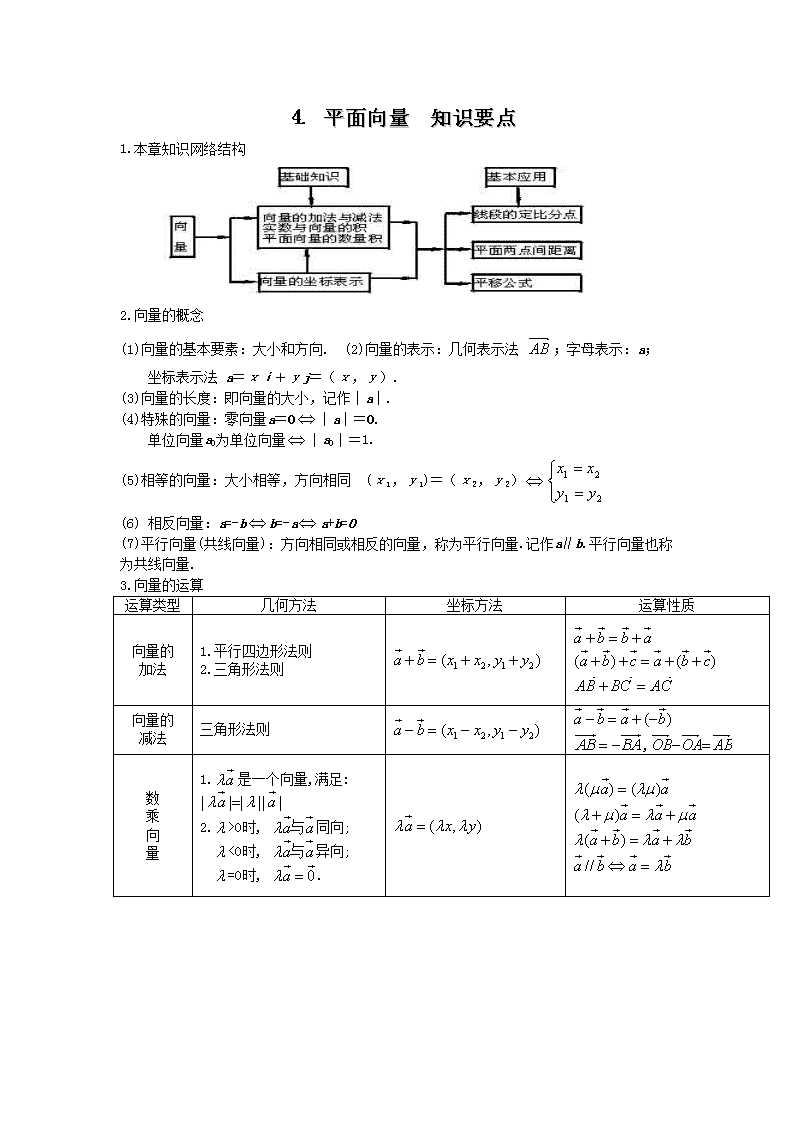
1.本章知识网络结构
2.向量的概念
(1)向量的基本要素:大小和方向.(2)向量的表示:几何表示法 ;字母表示:a;
坐标表示法 a=xi+yj=(x,y).
(3)向量的长度:即向量的大小,记作|a|.
(4)特殊的向量:零向量a=O|a|=O.
单位向量aO为单位向量|aO|=1.
(5)相等的向量:大小相等,方向相同(x1,y1)=(x2,y2)
(6) 相反向量:a=-bb=-aa+b=0
(7)平行向量(共线向量):方向相同或相反的向量,称为平行向量.记作a∥b.平行向量也称为共线向量.
3.向量的运算
运算类型
几何方法
坐标方法
运算性质
向量的
加法
1.平行四边形法则
2.三角形法则
向量的
减法
三角形法则
,
数
乘
向
量
1.是一个向量,满足:
2.>0时, 同向;
<0时, 异向;
=0时, .
向
量
的
数
量
积
是一个数
1.时,
.
2.
4.重要定理、公式
(1)平面向量基本定理
e1,e2是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有一对实数λ1,
λ2,使a=λ1e1+λ2e2.
(2)两个向量平行的充要条件
a∥ba=λb(b≠0)x1y2-x2y1=O.
(3)两个向量垂直的充要条件
a⊥ba·b=Ox1x2+y1y 2=O.
(4)线段的定比分点公式
设点P分有向线段所成的比为λ,即=λ,则
=+ (线段的定比分点的向量公式)
(线段定比分点的坐标公式)
当λ=1时,得中点公式:
=(+)或
(5)平移公式
设点P(x,y)按向量a=(h,k)平移后得到点P′(x′,y′),
则=+a或
曲线y=f(x)按向量a=(h,k)平移后所得的曲线的函数解析式为:
y-k=f(x-h)
(6)正、余弦定理
正弦定理:
余弦定理:a2=b2+c2-2bccosA,
b2=c2+a2-2cacosB,
c2=a2+b2-2abcosC.
(7)三角形面积计算公式:
设△ABC的三边为a,b,c,其高分别为ha,hb,hc,半周长为P,外接圆、内切圆的半径为R,r.
①S△=1/2aha=1/2bhb=1/2chc ②S△=Pr ③S△=abc/4R
④S△=1/2sinC·ab=1/2ac·sinB=1/2cb·sinA ⑤S△= [海伦公式]
⑥S△=1/2(b+c-a)ra[如下图]=1/2(b+a-c)rc=1/2(a+c-b)rb
[注]:到三角形三边的距离相等的点有4个,一个是内心,其余3个是旁心.
如图:
图1中的I为S△ABC的内心, S△=Pr
图2中的I为S△ABC的一个旁心,S△=1/2(b+c-a)ra
附:三角形的五个“心”;
重心:三角形三条中线交点.
外心:三角形三边垂直平分线相交于一点.
内心:三角形三内角的平分线相交于一点.
垂心:三角形三边上的高相交于一点.
旁心:三角形一内角的平分线与另两条内角的外角平分线相交一点.
⑸已知⊙O是△ABC的内切圆,若BC=a,AC=b,AB=c [注:s为△ABC的半周长,即]
则:①AE==1/2(b+c-a)
②BN==1/2(a+c-b)
③FC==1/2(a+b-c)
综合上述:由已知得,一个角的邻边的切线长,等于半周长减去对边(如图4).
特例:已知在Rt△ABC,c为斜边,则内切圆半径r=(如图3).
⑹在△ABC中,有下列等式成立.
证明:因为所以,所以,结论!
⑺在△ABC中,D是BC上任意一点,则.
证明:在△ABCD中,由余弦定理,有①
在△ABC中,由余弦定理有②,②代入①,化简
可得,(斯德瓦定理)
①若AD是BC上的中线,;
②若AD是∠A的平分线,,其中为半周长;
③若AD是BC上的高,,其中为半周长.
⑻△ABC的判定:
△ABC为直角△∠A + ∠B =
<△ABC为钝角△∠A + ∠B<
>△ABC为锐角△∠A + ∠B>
附:证明:,得在钝角△ABC中,
⑼平行四边形对角线定理:对角线的平方和等于四边的平方和.
空间向量
1.空间向量的概念:
具有大小和方向的量叫做向量
注:⑴空间的一个平移就是一个向量
⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量
⑶空间的两个向量可用同一平面内的两条有向线段来表示
2.空间向量的运算
定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下
运算律:⑴加法交换律:
⑵加法结合律:
⑶数乘分配律:
3共线向量
表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.平行于记作.
当我们说向量、共线(或//)时,表示、的有向线段所在的直线可能是同一直线,也可能是平行直线.
4.共线向量定理及其推论:
共线向量定理:空间任意两个向量、(≠),//的充要条件是存在实数λ,使=λ.
推论:如果为经过已知点A且平行于已知非零向量的直线,那么对于任意一点O,点P在直线上的充要条件是存在实数t满足等式
.
其中向量叫做直线的方向向量.
5.向量与平面平行:
已知平面和向量,作,如果直线平行于或在内,那么我们说向量平行于平面,记作:.
通常我们把平行于同一平面的向量,叫做共面向量
说明:空间任意的两向量都是共面的
6.共面向量定理:
如果两个向量不共线,与向量共面的充要条件是存在实数使
推论:空间一点位于平面内的充分必要条件是存在有序实数对,使或对空间任一点,有 ①
①式叫做平面的向量表达式
7空间向量基本定理:
如果三个向量不共面,那么对空间任一向量,存在一个唯一的有序实数组,使
推论:设是不共面的四点,则对空间任一点,都存在唯一的三个
有序实数,使
8空间向量的夹角及其表示:
已知两非零向量,在空间任取一点,作,则叫做向量与的夹角,记作;且规定,显然有;若,则称与互相垂直,记作:.
9.向量的模:
设,则有向线段的长度叫做向量的长度或模,记作:.
10.向量的数量积: .
已知向量和轴,是上与同方向的单位向量,作点在上的射影,作点在上的射影,则叫做向量在轴上或在上的正射影.
可以证明的长度.
11.空间向量数量积的性质:
(1).(2).(3).
12.空间向量数量积运算律:
(1).(2)(交换律)(3)(分配律).
空间向量的坐标运算
一.知识回顾:
(1)空间向量的坐标:空间直角坐标系的x轴是横轴(对应为横坐标),y轴是纵轴(对应为纵轴),z轴是竖轴(对应为竖坐标).
①令=(a1,a2,a3),,则
∥
(用到常用的向量模与向量之间的转化:)
②空间两点的距离公式:.
(2)法向量:若向量所在直线垂直于平面,则称这个向量垂直于平面,记作
,如果那么向量叫做平面的法向量.
(3)用向量的常用方法:
①利用法向量求点到面的距离定理:如图,设n是平面的法向量,AB是平面的一条射线,其中,则点B到平面的距离为.
②利用法向量求二面角的平面角定理:设分别是二面角中平面的法向量,则所成的角就是所求二面角的平面角或其补角大小(方向相同,则为补角,反方,则为其夹角).
③证直线和平面平行定理:已知直线平面,,且CDE三点不共线,则a∥的充要条件是存在有序实数对使.(常设求解若存在即证毕,若不存在,则直线AB与平面相交).