高考数学快速提升成绩题型训练——三角函数 17页

n 运算能力主要是指在运算定律和定理的指导下，对数和式的组合或分解变形能力，包括数字的计算，代数式和某些超越式的恒等变形，集合的运算，解方程和不等式，三角恒等变形，数列极限的计算，几何图形中的计算等。‎ n 运算准确 运算熟练 运算合理（是核心）运算的简捷。‎ ‎2009届高考数学快速提升成绩题型训练——三角函数 ‎1. 右图为 的图象的一段，求其解析式。‎ ‎2 设函数图像的一条对称轴是直线。‎ ‎（Ⅰ）求；（Ⅱ）求函数的单调增区间；w.w.w.k.s.5.u.c.o.m ‎（Ⅲ）画出函数在区间上的图像。‎ ‎3. 已知函数，‎ ‎（1）求它的定义域和值域；（2）求它的单调区间；（3）判断它的奇偶性；‎ ‎（4）判断它的周期性，如果是周期函数，求出它的最小正周期。‎ ‎4. 已知向量= (，2)，=(，（。‎ ‎（1）若，且的最小正周期为，求的最大值，并求取得最大值时的集合；‎ ‎（2）在（1）的条件下，沿向量平移可得到函数求向量。‎ ‎5. 设函数的图象经过两点（0，1），（），且在，求实数a的的取值范围.‎ ‎6. 若函数的最大值为，试确定常数a的值.‎ ‎7. 已知二次函数对任意，都有成立，设向量（sinx，2），（2sinx，），（cos2x，1），（1，2），当[0，]时，求不等式f（）＞f（）的解集．‎ ‎8. 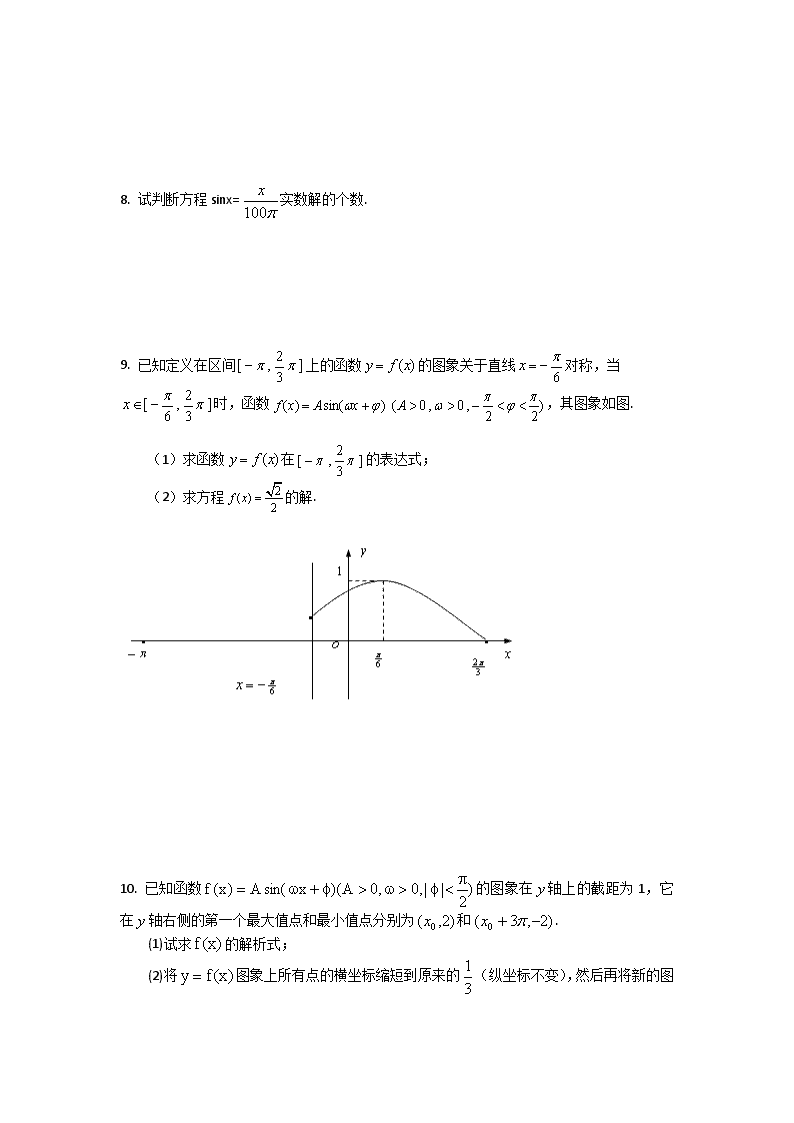试判断方程sinx=实数解的个数.‎ ‎9. 已知定义在区间上的函数的图象关于直线对称，当 时，函数，其图象如图.‎ ‎（1）求函数在的表达式；‎ ‎（2）求方程的解.‎ ‎10. 已知函数的图象在轴上的截距为1，它在轴右侧的第一个最大值点和最小值点分别为和. ‎ ‎(1)试求的解析式；‎ ‎(2)将图象上所有点的横坐标缩短到原来的 ‎（纵坐标不变），然后再将新的图象向轴正方向平移个单位，得到函数的图象.写出函数的解析式.‎ ‎11. 已知函数 ‎（Ⅰ）将f(x)写成的形式，并求其图象对称中心的横坐标及对称轴方程 ‎（Ⅱ）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的范围及此时函数f(x)的值域. ‎ ‎12. （ω＞0）‎ ‎（1）若f (x +θ)是周期为2π的偶函数，求ω及θ值 ‎（2）f (x)在（0，）上是增函数，求ω最大值。‎ ‎13. 已知且a∥b. 求的值.‎ ‎14. 已知△ABC三内角A、B、C所对的边a，b，c，且 ‎ （1）求∠B的大小；‎ ‎ （2）若△ABC的面积为，求b取最小值时的三角形形状.‎ ‎15. 求函数y=的值域.‎ ‎16. 求函数y=的单调区间.‎ ‎17. 已知 ‎①化简f(x);②若，且，求f(x)的值；‎ ‎18. 已知ΔABC的三个内角A、B、C成等差数列，且A