高考数学北京文试题及解析 9页

‎2017年高考数学北京文 ‎1.(2017年北京文)已知全集U=R，集合A={x|x＜-2或x＞2}，则∁uA=（ ）‎ A.（-2，2） B.（-∞，-2）∪（2，+∞）‎ C.[-2，2] D. （-∞，-2] ∪[2，+∞）‎ ‎1.C 【解析】因为A={x|x＜-2或x＞2}，所以∁uA={x|-2≤x≤2}.故选C.‎ ‎2. (2017年北京文)若复数（1-i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是（ ）‎ A. （-∞，1） B. （-∞，-1）‎ C. （1，+∞） D. （-1，+∞）‎ ‎2. C 【解析】设（1-i）（a+i）=（a+1）+（1-a）i，因为复数对应的点在第二象限，所以解得a＜-1.故选B.‎ ‎3. (2017年北京文)执行如图所示的程序框图，输出的s值为（ ）‎ A.2 B. C. D. ‎3. C 【解析】k=0时，0＜3成立，第一次进入循环：k=1，s==2；1＜3成立，第二次进入循环：k=2，s==；2＜3成立，第三次进入循环：k=3，s==，3＜3不成立，输出s=.故选C.‎ ‎4. (2017年北京文)若x，y满足则x+2y的最大值为（ ）‎ A.1 B.3 C.5 D.9‎ ‎4. D 【解析】如图，画出可行域，‎ z=x+2y表示斜率为-的一组平行线，当z=x+2y过点C（3，3）时，目标函数取得最大值zmax=3+2×3=9.故选D.‎ ‎5. (2017年北京文)已知函数f（x）=3x-（）x，则f（x）（ ）‎ A.是偶函数，且在R上是增函数 B.是奇函数，且在R上是增函数 C.是偶函数，且在R上是减函数 D.是奇函数，且在R上是减函数 ‎5. 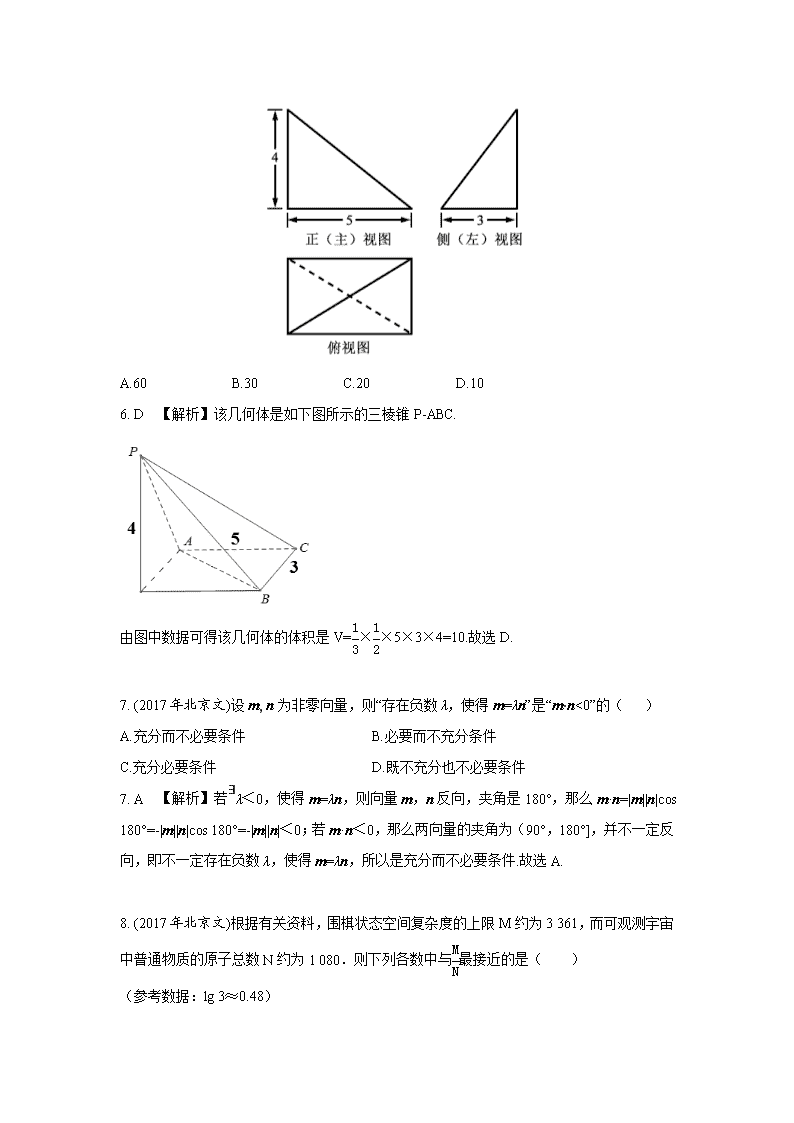B 【解析】f（-x）=3-x-（）-x=（）x-3x=-f（x），所以该函数是奇函数，并且y=3x是增函数，y=（）x是减函数，根据增函数-减函数=增函数，可知该函数是增函数.故选B.‎ ‎6. (2017年北京文)某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）‎ A.60 B.30 C.20 D.10‎ ‎6. D 【解析】该几何体是如下图所示的三棱锥P-ABC.‎ 由图中数据可得该几何体的体积是V=××5×3×4=10.故选D.‎ ‎7. (2017年北京文)设m, n为非零向量，则“存在负数λ，使得m=λn”是“m·n<0”的（ ）‎ A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎7. A 【解析】若∃λ＜0，使得m=λn，则向量m，n反向，夹角是180°，那么m·n=|m||n|cos 180°=-|m||n|cos 180°=-|m||n|＜0；若m·n＜0，那么两向量的夹角为（90°，180°]，并不一定反向，即不一定存在负数λ，使得m=λn，所以是充分而不必要条件.故选A.‎ ‎8. (2017年北京文)根据有关资料，围棋状态空间复杂度的上限M约为3 361，而可观测宇宙中普通物质的原子总数N约为1 080．则下列各数中与最接近的是（ ）‎ ‎（参考数据：lg 3≈0.48）‎ A.1033 B.1053‎ C.1073 D.1093‎ ‎8. D 【解析】设=x==lg 3361-lg 1080=361×lg 3-80=93.28，所以x=1093.28，即最接近1093.故选D.‎ ‎9. (2017年北京文)在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称.若sin α=，则sin β=_________．‎ ‎9. 【解析】因为角α与角β的终边关于轴对称，所以α+β=π+2kπ，k∈Z，所以sin β=sin（π+2kπ-α）=sin α=.‎ ‎10. (2017年北京文)若双曲线x2-=1的离心率为，则实数m=_________．‎ ‎10. 2 【解析】因为a2=1，b2=m，所以==，解得m=2.‎ ‎11. (2017年北京文)已知x≥0，y≥0，且x+y=1，则x2+y2的取值范围是_________．‎ ‎11. [,1] 【解析】x2+y2=x2+（1-x）2=2x2-2x+1，x∈[0，1]，所以当x=0或1时，取最大值1；当x= 时，取最小值.因此x2+y2的取值范围为[,1].‎ ‎12. (2017年北京文)已知点P在圆x2+y2=1上，点A的坐标为（-2，0），O为原点，则·的最大值为_________．‎ ‎12. 6 【解析】·=||·||cos θ≤||·||≤2×（2+1）=6.所以最大值是6.‎ ‎13. (2017年北京文)能够说明“设a，b，c是任意实数．若a>b>c，则a+b>c”是假命题的一组整数a,b,c的值依次为_________．‎ ‎13. −1，−2，−3（答案不唯一） 【解析】-1＞-2＞-3，-1+（-2）=-3＞-3，矛盾，所以-1，-2，-3可验证该命题是假命题.‎ ‎14. (2017年北京文)某学习小组由学生和教师组成，人员构成同时满足以下三个条件：‎ ‎（ⅰ）男学生人数多于女学生人数；‎ ‎（ⅱ）女学生人数多于教师人数；‎ ‎（ⅲ）教师人数的两倍多于男学生人数．‎ ‎①若教师人数为4，则女学生人数的最大值为_________．‎ ‎②该小组人数的最小值为_________．‎ ‎14. 6 12 【解析】设男生人数、女生人数、教师人数分别为a，b，c，则2c＞a＞b＞c，a，b，c，∈N*.‎ ‎①8＞a＞b＞4bmax=6，‎ ‎②cmin=3，6＞a＞b＞3a=5，b=4a+b+c=12.‎ ‎15. (2017年北京文)已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5．‎ ‎（1）求{an}的通项公式；‎ ‎（2）求和：b1+b3+b5+…b2n-1．‎ ‎15.解：（1）设等差数列{an}的公差为d.‎ 因为a2+a4=10，∴2a1+4d=10.‎ 解得d=2.‎ 所以an=2n-1.‎ ‎（2）设等比数列{bn}的公比为q.‎ 因为b2b4=a5，所以b1qb1q3=9.‎ 解得q2=3.‎ 所以b2n-1=b1q2n-2=3n-1.‎ 从而b1+b3+b5+…b2n-1=1+3+32+…+3n-1=.‎ ‎16. (2017年北京文)已知函数f（x）=cos（2x-）-2sin xcos x.‎ ‎（1）求f(x)的最小正周期；‎ ‎（2）求证：当x∈[-，]时，f（x）≥-．‎ ‎16.解：f（x）=cos 2x+sin 2x-sin 2x=sin 2x+cos 2x=sin（2x+）.‎ 所以f（x）的最小正周期T==π.‎ ‎（2）因为-≤x≤，‎ 所以-≤2x+≤.‎ 所以sin（2x+）≥sin（-）=-.‎ 所以当x∈[-，]时，f（x）≥-.‎ ‎17. (2017年北京文)某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30]，[30,40]，…，[80,90]，并整理得到如下频率分布直方图：‎ ‎（1）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；‎ ‎（2）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50)内的人数；‎ ‎（3）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．‎ ‎17.解：根据频率分布直方图可知，样本中分数不小于70的频率为（0.02+0.04）×10=0.6，所以样本中分数小于70的频率为1-0.6=0.4.‎ 所以从总体的400名学生中随机抽取一人，其分数小于70的概率估计为0.4.‎ ‎（2）根据题意，样本中分数不小于50的频率为（0.01+0.02+0.04+0.02）×10=0.9，分数在区间[40，50）内的人数为100-100×0.9-5=5.‎ 所以总体中分数在区间[40，50）内的人数估计为400×=20.‎ ‎（3）由题意可知，样本中分数不小于70的学生人数为（0.02+0.04）×10×100=60，‎ 所以样本中分数不小于70的男生人数为60×=30.‎ 所以样本中的男生人数为30×2=60，女生人数为100-60=40，男生和女生人数的比例为60：40=3：2.‎ 所以根据分层抽样原理，总体中男生和女生人数的比例估计为3：2.‎ ‎18. (2017年北京文)如图，在三棱锥P–ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．‎ ‎（1）求证：PA⊥BD；‎ ‎（2）求证：平面BDE⊥平面PAC；‎ ‎（3）当PA∥平面BDE时，求三棱锥E–BCD的体积．‎ ‎18.解：（1）因为PA⊥AB，PA⊥BC，所以PA⊥平面ABC，‎ 又因为BD⊂平面ABC，所以PA⊥BD.‎ ‎（2）因为AB=BC，D为AC中点，所以BD⊥AC，‎ 由（1）知，PA⊥BD，所以BD⊥平面PAC，‎ 所以平面BDE⊥平面PAC.‎ ‎（3）因为PA∥平面BDE，平面PAC∩平面BDE=DE，‎ 所以PA∥DE.‎ 因为D为AC的中点，所以DE=PA=1，BD=DC=.‎ 由（1）知，PA⊥平面ABC，所以DE⊥平面ABC.‎ 所以三棱锥E-BCD的体积V=BD·DC·DE=.‎ ‎19. (2017年北京文)已知椭圆C的两个顶点分别为A(−2,0)，B(2,0)，焦点在x 轴上，离心率为．‎ ‎（1）求椭圆C的方程；‎ ‎（2）点D为x轴上一点，过D作x轴的垂线交椭圆C于不同的两点M，N，过D作AM的垂线交BN于点E.求证：△BDE与△BDN的面积之比为4:5．‎ ‎19.解：（1）设椭圆C的方程为+=1（a＞b＞0）.‎ 由题意得解得c=.‎ 所以b2=a2-c2=1.‎ 所以椭圆C的方程为+y2=1.‎ ‎（2）设M（m，n），则D（m，0），N（m，-n）.‎ 由题设知m≠±2，且n≠0.‎ 直线AM的斜率kAM=，故直线DE的斜率kDE=-.‎ 所以直线DE的方程为y=-（x-m）.‎ 直线BN的方程为y=（x-2）.‎ 联立解得点E的纵坐标yE=.‎ 由点M在椭圆C上，得4-m2=4n2.‎ 所以yE=-n.‎ 又S△BDE=|BD|·|yE|=|BD|·|n|，‎ S△BDN=|BD|·|n|，‎ 所以△BDE与△BDN的面积之比为4：5.‎ ‎20. (2017年北京文)已知函数f（x）=excos x-x．‎ ‎（1）求曲线y=f（x）在点（0，f（0））处的切线方程；‎ ‎（2）求函数f（x）在区间[0，]上的最大值和最小值．‎ ‎20.解：（1）因为f（x）=excos x-x，所以f′（x）=ex（cos x-sin x）-1，f′（0）=0.‎ 又因为f（0）=1，所以曲线y=f（x）在点（0，f（0））处的切线方程为y=1.‎ ‎（2）设h（x）= ex（cos x-sin x）-1，则h′（x）= ex（cos x-sin x-sin x-cos x）-2exsin x.‎ 当x∈（0，）时，h′（x）＜0，‎ 所以h（x）在区间[0，]上单调递减.‎ 所以对任意x∈[0，]有h（x）＜h（0）=0，即f′（x）＜0.‎ 所以函数f（x）在区间[0，]上单调递减.‎ 因此f（x）在区间[0，]上的最大值为f（0）=1，最小值为f（）=-.‎