上海市嘉定区高考数学二模试卷含答案解析 21页

‎2017年上海市嘉定区高考数学二模试卷 ‎　‎ 一、填空题（本大题共有12题，满分54分，第1～6题每题4分，第7～12题每题5分）考生应在答题纸的相应位置直接填写结果．‎ ‎1．函数y=2sin2（2x）﹣1的最小正周期是　　．‎ ‎2．设i为虚数单位，复数，则|z|=　　．‎ ‎3．设f﹣1（x）为的反函数，则f﹣1（1）=　　．‎ ‎4． =　　．‎ ‎5．若圆锥的侧面积是底面积的2倍，则其母线与轴所成角的大小是　　．‎ ‎6．设等差数列{an}的前n项和为Sn，若=，则=　　．‎ ‎7．直线（t为参数）与曲线（θ为参数）的公共点的个数是　　．‎ ‎8．已知双曲线C1与双曲线C2的焦点重合，C1的方程为，若C2的一条渐近线的倾斜角是C1的一条渐近线的倾斜角的2倍，则C2的方程为　　．‎ ‎9．若，则满足f（x）＞0的x的取值范围是　　．‎ ‎10．某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为和．现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立，则至少有一种新产品研发成功的概率为　　．‎ ‎11．设等差数列{an}的各项都是正数，前n项和为Sn，公差为d．若数列也是公差为d的等差数列，则{an}的通项公式为an=　　．‎ ‎12．设x∈R，用[x]表示不超过x的最大整数（如[2.32]=2，[﹣4.76]=﹣5），对于给定的n∈N*，定义C=，其中x∈[1，+∞），则当时，函数f（x）=C的值域是　　．‎ ‎　‎ 二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项．考生应在答题纸的相应位置，将代表正确选项的小方格涂黑．‎ ‎13．命题“若x=1，则x2﹣3x+2=0”的逆否命题是（　　）‎ A．若x≠1，则x2﹣3x+2≠0 B．若x2﹣3x+2=0，则x=1‎ C．若x2﹣3x+2=0，则x≠1 D．若x2﹣3x+2≠0，则x≠1‎ ‎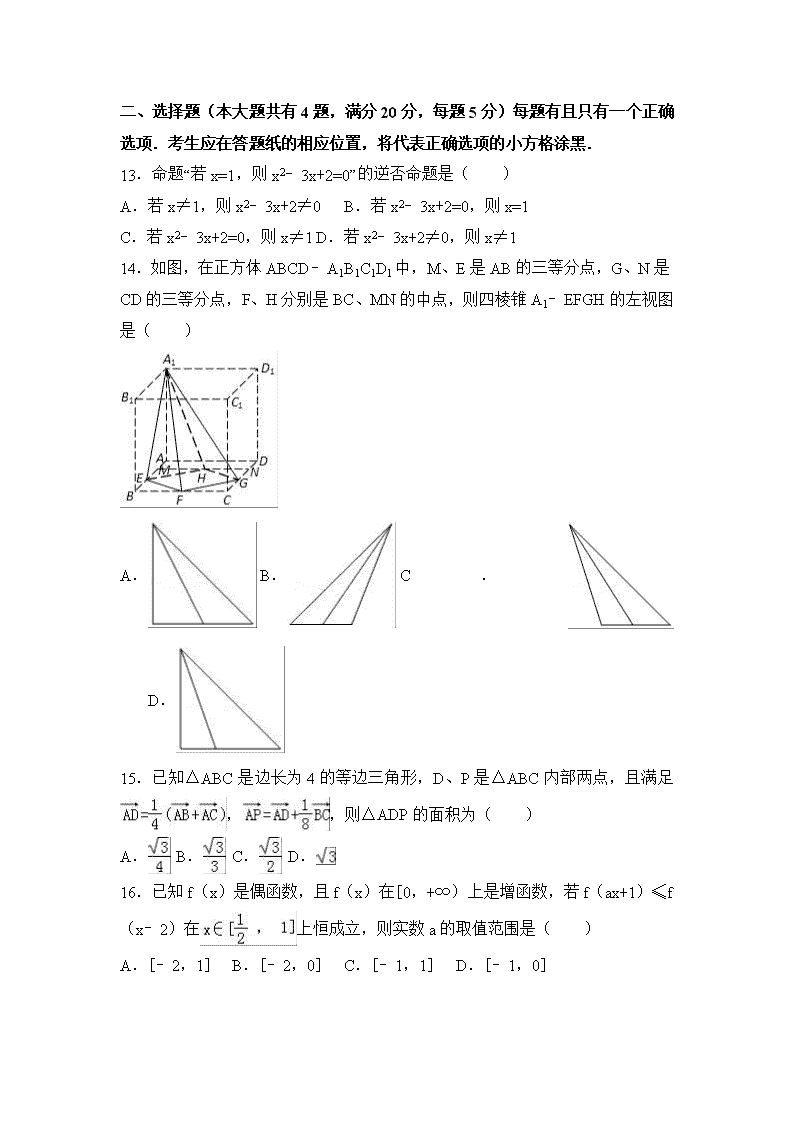14．如图，在正方体ABCD﹣A1B1C1D1中，M、E是AB的三等分点，G、N是CD的三等分点，F、H分别是BC、MN的中点，则四棱锥A1﹣EFGH的左视图是（　　）‎ A． B． C． D．‎ ‎15．已知△ABC是边长为4的等边三角形，D、P是△ABC内部两点，且满足，，则△ADP的面积为（　　）‎ A． B． C． D．‎ ‎16．已知f（x）是偶函数，且f（x）在[0，+∞）上是增函数，若f（ax+1）≤f（x﹣2）在上恒成立，则实数a的取值范围是（　　）‎ A．[﹣2，1] B．[﹣2，0] C．[﹣1，1] D．[﹣1，0]‎ ‎　‎ 三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸的相应位置写出必要的步骤．‎ ‎17．在△ABC中，内角A，B，C的对边分别为a，b，c，已知a﹣b=2，c=4，sinA=2sinB．‎ ‎（Ⅰ）求△ABC的面积；‎ ‎（Ⅱ）求sin（2A﹣B）．‎ ‎18．如图，在长方体ABCD﹣A1B1C1D1中，AB=8，BC=5，AA1=4，平面α截长方体得到一个矩形EFGH，且A1E=D1F=2，AH=DG=5．‎ ‎（1）求截面EFGH把该长方体分成的两部分体积之比；‎ ‎（2）求直线AF与平面α所成角的正弦值．‎ ‎19．如图，已知椭圆C：（a＞b＞0）过点，两个焦点为F1（﹣1，0）和F2（1，0）．圆O的方程为x2+y2=a2．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）过F1且斜率为k（k＞0）的动直线l与椭圆C交于A、B两点，与圆O交于P、Q两点（点A、P在x轴上方），当|AF2|，|BF2|，|AB|成等差数列时，求弦PQ的长．‎ ‎20．如果函数y=f（x）的定义域为R，且存在实常数a，使得对于定义域内任意x，都有f（x+a）=f（﹣x）成立，则称此函数f（x）具有“P（a）性质”．‎ ‎（1）判断函数y=cosx是否具有“P（a）性质”，若具有“P（a）性质”，求出所有a的值的集合；若不具有“P（a）性质”，请说明理由；‎ ‎（2）已知函数y=f（x）具有“P（0）性质”，且当x≤0时，f（x）=（x+m）2，求函数y=f（x）在区间[0，1]上的值域；‎ ‎（3）已知函数y=g（x）既具有“P（0）性质”，又具有“P（2）性质”，且当﹣1≤x≤1时，g（x）=|x|，若函数y=g（x）的图象与直线y=px有2017个公共点，求实数p的值．‎ ‎21．给定数列{an}，若满足a1=a（a＞0且a≠1），对于任意的n，m∈N*，都有an+m=an•am，则称数列{an}为指数数列．‎ ‎（1）已知数列{an}，{bn}的通项公式分别为，，试判断{an}，{bn}是不是指数数列（需说明理由）；‎ ‎（2）若数列{an}满足：a1=2，a2=4，an+2=3an+1﹣2an，证明：{an}是指数数列；‎ ‎（3）若数列{an}是指数数列，（t∈N*），证明：数列{an}中任意三项都不能构成等差数列．‎ ‎　‎ ‎2017年上海市嘉定区高考数学二模试卷 参考答案与试题解析 ‎　‎ 一、填空题（本大题共有12题，满分54分，第1～6题每题4分，第7～12题每题5分）考生应在答题纸的相应位置直接填写结果．‎ ‎1．函数y=2sin2（2x）﹣1的最小正周期是　　．‎ ‎【考点】H1：三角函数的周期性及其求法．‎ ‎【分析】利用二倍角公式基本公式将函数化为y=Acos（ωx+φ）的形式，再利用周期公式求函数的最小正周期，‎ ‎【解答】解：函数y=2sin2（2x）﹣1，‎ 化简可得：y=1﹣cos4x﹣1=﹣cos4x；‎ ‎∴最小正周期T=．‎ 故答案为 ‎　‎ ‎2．设i为虚数单位，复数，则|z|=　1　．‎ ‎【考点】A8：复数求模．‎ ‎【分析】利用复数的运算法则、模的计算公式即可得出．‎ ‎【解答】解：复数===﹣i，‎ 则|z|=1．‎ 故答案为：1．‎ ‎　‎ ‎3．设f﹣1（x）为的反函数，则f﹣1（1）=　1　．‎ ‎【考点】4R：反函数．‎ ‎【分析】根据反函数的性质，原函数的值域是反函数的定义域即可求解 ‎【解答】解：的反函数，‎ 其反函数f﹣1（x），‎ 反函数的性质，反函数的定义域是原函数的值域，即．‎ 可得：x=1，‎ ‎∴f﹣1（x）=1．‎ 故答案为1．‎ ‎　‎ ‎4． =　3　．‎ ‎【考点】8J：数列的极限．‎ ‎【分析】通过分子分母同除3n+1，利用数列极限的运算法则求解即可．‎ ‎【解答】解： ===3．‎ 故答案为：3．‎ ‎　‎ ‎5．若圆锥的侧面积是底面积的2倍，则其母线与轴所成角的大小是　30°　．‎ ‎【考点】MI：直线与平面所成的角．‎ ‎【分析】根据圆锥的底面积公式和侧面积公式，结合已知可得l=2R，进而解母线与底面所成角，然后求解母线与轴所成角即可．‎ ‎【解答】解：设圆锥的底面半径为R，母线长为l，则：‎ 其底面积：S底面积=πR2，‎ 其侧面积：S侧面积=2πRl=πRl，‎ ‎∵圆锥的侧面积是其底面积的2倍，‎ ‎∴l=2R，‎ 故该圆锥的母线与底面所成的角θ有，‎ cosθ==，‎ ‎∴θ=60°，‎ 母线与轴所成角的大小是：30°．‎ 故答案为：30°．‎ ‎　‎ ‎6．设等差数列{an}的前n项和为Sn，若=，则=　　．‎ ‎【考点】85：等差数列的前n项和．‎ ‎【分析】=，可得3（a1+4d）=5（a1+2d），化为：a1=d．再利用等差数列的求和公式即可得出．‎ ‎【解答】解：∵=，∴3（a1+4d）=5（a1+2d），化为：a1=d．‎ 则==．‎ 故答案为：．‎ ‎　‎ ‎7．直线（t为参数）与曲线（θ为参数）的公共点的个数是　1　．‎ ‎【考点】QK：圆的参数方程；QJ：直线的参数方程．‎ ‎【分析】根据题意，将直线的参数方程变形为普通方程，再将曲线的参数方程变形为普通方程，分析可得该曲线为圆，且圆心坐标为（3，5），半径r=，求出圆心到直线的俄距离，分析可得直线与圆相切，即可得直线与圆有1个公共点，即可得答案．‎ ‎【解答】解：根据题意，直线的参数方程为，则其普通方程为x+y﹣6=0，‎ 曲线的参数方程为，则其普通方程为（x﹣3）2+（y﹣5）2=2，该曲线为圆，且圆心坐标为（3，5），半径r=，‎ 圆心到直线x+y﹣6=0的距离d===r，‎ 则圆（x﹣3）2+（y﹣5）2=2与直线x+y﹣6=0相切，有1个公共点；‎ 故答案为：1．‎ ‎　‎ ‎8．已知双曲线C1与双曲线C2的焦点重合，C1的方程为，若C2的一条渐近线的倾斜角是C1的一条渐近线的倾斜角的2倍，则C2的方程为　　．‎ ‎【考点】KC：双曲线的简单性质．‎ ‎【分析】求出双曲线的焦点坐标，利用渐近线的倾斜角的关系，列出方程，然后求解即可．‎ ‎【解答】解：双曲线C1与双曲线C2的焦点重合，C1的方程为，焦点坐标（±2，0）．‎ 双曲线C1的一条渐近线为：y=，倾斜角为30°，‎ C2的一条渐近线的倾斜角是C1的一条渐近线的倾斜角的2倍，可得C2的渐近线y=．‎ 可得，c=2，解得a=1，b=，‎ 所求双曲线方程为：．‎ 故答案为：．‎ ‎　‎ ‎9．若，则满足f（x）＞0的x的取值范围是　（1，+∞）　．‎ ‎【考点】7E：其他不等式的解法．‎ ‎【分析】由已知得到关于x的不等式，化为根式不等式，然后化为整式不等式解之．‎ ‎【解答】解：由f（x）＞0得到即，所以，解得x＞1；‎ 故x的取值范围为（1，+∞）；‎ 故答案为：（1，+∞）；‎ ‎　‎ ‎10．某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为和 ‎．现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立，则至少有一种新产品研发成功的概率为　　．‎ ‎【考点】C9：相互独立事件的概率乘法公式．‎ ‎【分析】利用对立事件的概率公式，计算即可，‎ ‎【解答】解：设至少有一种新产品研发成功的事件为事件A且事件B为事件A的对立事件，则事件B为一种新产品都没有成功，‎ 因为甲乙研发新产品成功的概率分别为和．‎ 则P（B）=（1﹣）（1﹣）=，‎ 再根据对立事件的概率之间的公式可得P（A）=1﹣P（B）=，‎ 故至少有一种新产品研发成功的概率．‎ 故答案为．‎ ‎　‎ ‎11．设等差数列{an}的各项都是正数，前n项和为Sn，公差为d．若数列也是公差为d的等差数列，则{an}的通项公式为an=　　．‎ ‎【考点】84：等差数列的通项公式．‎ ‎【分析】由题意可得：Sn=na1+d．an＞0. = +（n﹣1）d，化简n≠1时可得：a1=（n﹣1）d2+2d﹣d．分别令n=2，3，解出即可得出．‎ ‎【解答】解：由题意可得：Sn=na1+d．an＞0．‎ ‎=+（n﹣1）d，可得：Sn=a1+（n﹣1）2d2+2（n﹣1）d．‎ ‎∴na1+d=a1+（n﹣1）2d2+2（n﹣1）d．‎ n≠1时可得：a1=（n﹣1）d2+2d﹣d．‎ 分别令n=2，3，可得：a1=d2+2d﹣d，a1=2d2+2d﹣d．‎ 解得a1=，d=．‎ ‎∴an=+（n﹣1）=．‎ 故答案为：．‎ ‎　‎ ‎12．设x∈R，用[x]表示不超过x的最大整数（如[2.32]=2，[﹣4.76]=﹣5），对于给定的n∈N*，定义C=，其中x∈[1，+∞），则当时，函数f（x）=C的值域是　　．‎ ‎【考点】57：函数与方程的综合运用．‎ ‎【分析】分类讨论，根据定义化简Cxn，求出Cx10的表达式，再利用函数的单调性求出Cx10的值域．‎ ‎【解答】解：当x∈[，2）时，[x]=1，∴f（x）=C=，‎ 当x∈[，2）时，f（x）是减函数，∴f（x）∈（5，）；‎ 当x∈[2，3）时，[x]=2，∴f（x）=C=，‎ 当x∈[2，3）时，f（x）是减函数，∴f（x）∈（15，45]；‎ ‎∴当时，函数f（x）=C的值域是，‎ 故答案为：．‎ ‎　‎ 二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项．考生应在答题纸的相应位置，将代表正确选项的小方格涂黑．‎ ‎13．命题“若x=1，则x2﹣3x+2=0”的逆否命题是（　　）‎ A．若x≠1，则x2﹣3x+2≠0 B．若x2﹣3x+2=0，则x=1‎ C．若x2﹣3x+2=0，则x≠1 D．若x2﹣3x+2≠0，则x≠1‎ ‎【考点】25：四种命题间的逆否关系．‎ ‎【分析】根据逆否命题的定义，我们易求出命题的逆否命题 ‎【解答】解：将命题的条件与结论交换，并且否定可得逆否命题：若x2﹣3x+2≠0，则x≠1‎ 故选：D ‎　‎ ‎14．如图，在正方体ABCD﹣A1B1C1D1‎ 中，M、E是AB的三等分点，G、N是CD的三等分点，F、H分别是BC、MN的中点，则四棱锥A1﹣EFGH的左视图是（　　）‎ A． B． C． D．‎ ‎【考点】L7：简单空间图形的三视图．‎ ‎【分析】确定5个顶点在面DCC1D1上的投影，即可得出结论．‎ ‎【解答】解：A1在面DCC1D1上的投影为点D1，E在面DCC1D1的投影为点G，F在面DCC1D1上的投影为点C，H在面DCC1D1上的投影为点N，因此侧视图为选项C的图形．‎ 故选C ‎　‎ ‎15．已知△ABC是边长为4的等边三角形，D、P是△ABC内部两点，且满足，，则△ADP的面积为（　　）‎ A． B． C． D．‎ ‎【考点】9V：向量在几何中的应用．‎ ‎【分析】以A为原点，以BC的垂直平分线为y轴，建立直角坐标系．由于等边三角形△‎ 的边长为4，可得B，C的坐标，再利用向量的坐标运算和数乘运算可得，，利用△APD的面积公式即可得出．‎ ‎【解答】解：以A为原点，以BC的垂直平分线为y轴，建立直角坐标系．‎ ‎∵等边三角形△的边长为4，‎ ‎∴B（﹣2，﹣2），C（2，﹣2），‎ 由足= [（﹣2，﹣2）+（2，﹣2）]=（0，﹣），‎ ‎=（0，﹣）+（4，0）=（，﹣），‎ ‎∴△ADP的面积为S=||•||=××=，‎ 故选：A．‎ ‎　‎ ‎16．已知f（x）是偶函数，且f（x）在[0，+∞）上是增函数，若f（ax+1）≤f（x﹣2）在上恒成立，则实数a的取值范围是（　　）‎ A．[﹣2，1] B．[﹣2，0] C．[﹣1，1] D．[﹣1，0]‎ ‎【考点】3N：奇偶性与单调性的综合．‎ ‎【分析】因为偶函数在对称区间上单调性相反，根据已知中f（x）是偶函数，且f（x）在（0，+∞）上是增函数，易得f（x）在（﹣∞，0）上为减函数，又由若时，不等式f（ax+1）≤f（x﹣2）恒成立，结合函数恒成立的条件，求出时f（x﹣2）的最小值，从而可以构造一个关于a的不等式，解不等式即可得到实数a的取值范围．‎ ‎【解答】解：∵f（x）是偶函数，且f（x）在（0，+∞）上是增函数，‎ ‎∴f（x）在（﹣∞，0）上为减函数，‎ 当时，x﹣2∈[﹣，﹣1]，‎ 故f（x﹣2）≥f（﹣1）=f（1），‎ 若时，不等式f（ax+1）≤f（x﹣2）恒成立，‎ 则当时，|ax+1|≤1恒成立，‎ ‎∴﹣1≤ax+1≤1，∴≤a≤0，‎ ‎∴﹣2≤a≤0，‎ 故选B．‎ ‎　‎ 三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸的相应位置写出必要的步骤．‎ ‎17．在△ABC中，内角A，B，C的对边分别为a，b，c，已知a﹣b=2，c=4，sinA=2sinB．‎ ‎（Ⅰ）求△ABC的面积；‎ ‎（Ⅱ）求sin（2A﹣B）．‎ ‎【考点】GL：三角函数中的恒等变换应用．‎ ‎【分析】解法一：（I）由已知及正弦定理可求a，b的值，由余弦定理可求cosB，从而可求sinB，即可由三角形面积公式求解．‎ ‎（II）由余弦定理可得cosA，从而可求sinA，sin2A，cos2A，由两角差的正弦公式即可求sin（2A﹣B）的值．‎ 解法二：（I）由已知及正弦定理可求a，b的值，又c=4，可知△ABC为等腰三角形，作BD⊥AC于D，可求BD==，即可求三角形面积．‎ ‎（II）由余弦定理可得cosB，即可求sinB，由（I）知A=C⇒2A﹣B=π﹣2B．从而sin（2A﹣B）=sin（π﹣2B）=sin2B，代入即可求值．‎ ‎【解答】解：‎ 解法一：（I）由sinA=2sinB⇒a=2b．‎ 又∵a﹣b=2，‎ ‎∴a=4，b=2． ‎ cosB===． ‎ sinB===． ‎ ‎∴S△ABC=acsinB==． ‎ ‎（II）cosA===．‎ sinA===． ‎ sin2A=2sinAcosA=2×．‎ cos2A=cos2A﹣sin2A=﹣． ‎ ‎∴sin（2A﹣B）=sin2AcosB﹣cos2AsinB ‎==． ‎ 解法二：（I）由sinA=2sinB⇒a=2b．‎ 又∵a﹣b=2，‎ ‎∴a=4，b=2． ‎ 又c=4，可知△ABC为等腰三角形． ‎ 作BD⊥AC于D，则BD===． ‎ ‎∴S△ABC==．‎ ‎（II）cosB===． ‎ sinB===． ‎ 由（I）知A=C⇒2A﹣B=π﹣2B． ‎ ‎∴sin（2A﹣B）=sin（π﹣2B）=sin2B ‎=2sinBcosB ‎ ‎=2××=．‎ ‎　‎ ‎18．如图，在长方体ABCD﹣A1B1C1D1中，AB=8，BC=5，AA1=4，平面α截长方体得到一个矩形EFGH，且A1E=D1F=2，AH=DG=5．‎ ‎（1）求截面EFGH把该长方体分成的两部分体积之比；‎ ‎（2）求直线AF与平面α所成角的正弦值．‎ ‎【考点】MI：直线与平面所成的角；LF：棱柱、棱锥、棱台的体积．‎ ‎【分析】（1）由题意，平面α把长方体分成两个高为5的直四棱柱，转化求解体积推出结果即可．‎ ‎（2）解法一：作AM⊥EH，垂足为M，证明HG⊥AM，推出AM⊥平面EFGH．通过计算求出AM=4．AF，设直线AF与平面α所成角为θ，求解即可．‎ 解法二：以DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，求出平面α一个法向量，利用直线AF与平面α所成角为θ，通过空间向量的数量积求解即可．‎ ‎【解答】（本题满分，第1小题满分，第2小题满分8分）‎ 解：（1）由题意，平面α把长方体分成两个高为5的直四棱柱，‎ ‎，…‎ ‎，…‎ 所以，．…‎ ‎（2）解法一：作AM⊥EH，垂足为M，由题意，HG⊥平面ABB1A1，故HG⊥AM，‎ 所以AM⊥平面EFGH． …‎ 因为，，所以S△AEH=10，）‎ 因为EH=5，所以AM=4． …‎ 又，…‎ 设直线AF与平面α所成角为θ，则．…‎ 所以，直线AF与平面α所成角的正弦值为． …‎ 解法二：以DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，‎ 则A（5，0，0），H（5，5，0），E（5，2，4），F（0，2，4），…‎ 故，，…‎ 设平面α一个法向量为，则即 所以可取． …‎ 设直线AF与平面α所成角为θ，则． …‎ 所以，直线AF与平面α所成角的正弦值为． …‎ ‎　‎ ‎19．如图，已知椭圆C：（a＞b＞0）过点，两个焦点为F1（﹣1，0）和F2（1，0）．圆O的方程为x2+y2=a2．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）过F1且斜率为k（k＞0）的动直线l与椭圆C交于A、B两点，与圆O交于P、Q两点（点A、P在x轴上方），当|AF2|，|BF2|，|AB|‎ 成等差数列时，求弦PQ的长．‎ ‎【考点】KH：直线与圆锥曲线的综合问题；K3：椭圆的标准方程；KL：直线与椭圆的位置关系．‎ ‎【分析】（1）求出c=1，设椭圆C的方程为，将点代入，解得a2=4，然后求解椭圆C的方程．‎ ‎（2）由椭圆定义，|AF1|+|AF2|=4，|BF1|+|BF2|=4，通过|AF2|，|BF2|，|AB|成等差数列，推出． 设B（x0，y0），通过解得B，然后求解直线方程，推出弦PQ的长即可．‎ ‎【解答】（本题满分，第1小题满分，第2小题满分8分）‎ 解：（1）由题意，c=1，…‎ 设椭圆C的方程为，将点代入，‎ 解得a2=4（舍去），…‎ 所以，椭圆C的方程为． …‎ ‎（2）由椭圆定义，|AF1|+|AF2|=4，|BF1|+|BF2|=4，两式相加，得|AB|+|AF2|+|BF2|=8，‎ 因为|AF2|，|BF2|，|AB|成等差数列，所以|AB|+|AF2|=2|BF2|，‎ 于是3|BF2|=8，即． …‎ 设B（x0，y0），由解得，…‎ ‎（或设，则，解得，，所以）．‎ 所以，，直线l的方程为，即，…‎ 圆O的方程为x2+y2=4，圆心O到直线l的距离，…‎ 此时，弦PQ的长． …‎ ‎　‎ ‎20．如果函数y=f（x）的定义域为R，且存在实常数a，使得对于定义域内任意x，都有f（x+a）=f（﹣x）成立，则称此函数f（x）具有“P（a）性质”．‎ ‎（1）判断函数y=cosx是否具有“P（a）性质”，若具有“P（a）性质”，求出所有a的值的集合；若不具有“P（a）性质”，请说明理由；‎ ‎（2）已知函数y=f（x）具有“P（0）性质”，且当x≤0时，f（x）=（x+m）2，求函数y=f（x）在区间[0，1]上的值域；‎ ‎（3）已知函数y=g（x）既具有“P（0）性质”，又具有“P（2）性质”，且当﹣1≤x≤1时，g（x）=|x|，若函数y=g（x）的图象与直线y=px有2017个公共点，求实数p的值．‎ ‎【考点】57：函数与方程的综合运用．‎ ‎【分析】（1）根据题意可知cos（x+a）=cos（﹣x）=cosx，故而a=2kπ，k∈Z；‎ ‎（2）由新定义可推出f（x）为偶函数，从而求出f（x）在[0，1]上的解析式，讨论m与[0，1]的关系判断f（x）的单调性得出f（x）的最值；‎ ‎（3）根据新定义可知g（x）为周期为2的偶函数，作出g（x）的函数图象，根据函数图象得出p的值．‎ ‎【解答】解：（1）假设y=cosx具有“P（a）性质”，则cos（x+a）=cos（﹣x）=cosx恒成立，‎ ‎∵cos（x+2kπ）=cosx，‎ ‎∴函数y=cosx具有“P（a）性质”，且所有a的值的集合为{a|a=2kπ，k∈Z}． ‎ ‎（2）因为函数y=f（x）具有“P（0）性质”，所以f（x）=f（﹣x）恒成立，‎ ‎∴y=f（x）是偶函数． ‎ 设0≤x≤1，则﹣x≤0，∴f（x）=f（﹣x）=（﹣x+m）2=（x﹣m）2． ‎ ‎①当m≤0时，函数y=f（x）在[0，1]上递增，值域为[m2，（1﹣m）2]． ‎ ‎②当时，函数y=f（x）在[0，m]上递减，在[m，1]上递增，‎ ymin=f（m）=0，，值域为[0，（1﹣m）2]． ‎ ‎③当时，ymin=f（m）=0，，值域为[0，m2]．‎ ‎④m＞1时，函数y=f（x）在[0，1]上递减，值域为[（1﹣m）2，m2]． ‎ ‎（3）∵y=g（x）既具有“P（0）性质”，即g（x）=g（﹣x），∴函数y=g（x）偶函数，‎ 又y=g（x）既具有“P（2）性质”，即g（x+2）=g（﹣x）=g（x），‎ ‎∴函数y=g（x）是以2为周期的函数． ‎ 作出函数y=g（x）的图象如图所示：‎ 由图象可知，当p=0时，函数y=g（x）与直线y=px交于点（2k，0）（k∈Z），即有无数个交点，不合题意． ‎ 当p＞0时，在区间[0，2016]上，函数y=g（x）有1008个周期，要使函数y=g（x）的图象与直线y=px有2017个交点，‎ 则直线在每个周期内都有2个交点，且第2017个交点恰好为，所以．‎ 同理，当p＜0时，．‎ 综上，．‎ ‎　‎ ‎21．给定数列{an}，若满足a1=a（a＞0且a≠1），对于任意的n，m∈N*，都有an+m=an•am，则称数列{an}为指数数列．‎ ‎（1）已知数列{an}，{bn}的通项公式分别为，，试判断{an}，{bn}是不是指数数列（需说明理由）；‎ ‎（2）若数列{an}满足：a1=2，a2=4，an+2=3an+1﹣2an，证明：{an}是指数数列；‎ ‎（3）若数列{an}是指数数列，（t∈N*），证明：数列{an}中任意三项都不能构成等差数列．‎ ‎【考点】8B：数列的应用．‎ ‎【分析】（1）利用指数数列的定义，判断即可；‎ ‎（2）求出{an}的通项公式为，即可证明：{an}是指数数列；‎ ‎（3）利用反证法进行证明即可．‎ ‎【解答】（1）解：对于数列{an}，因为a3=a1+2≠a1•a2，所以{an}不是指数数列． …‎ 对于数列{bn}，对任意n，m∈N*，因为，‎ 所以{bn}是指数数列． …‎ ‎（2）证明：由题意，an+2﹣an+1=2（an+1﹣an），‎ 所以数列{an+1﹣an}是首项为a2﹣a1=2，公比为2的等比数列． …‎ 所以．所以，‎ ‎=，即{an}的通项公式为（n∈N*）． …‎ 所以，故{an}是指数数列． …‎ ‎（3）证明：因为数列{an}是指数数列，故对于任意的n，m∈N*，有an+m=an•am，令m=1，则，所以{an}是首项为，公比为的等比数列，‎ 所以，． …‎ 假设数列{an}中存在三项au，av，aw构成等差数列，不妨设u＜v＜w，‎ 则由2av=au+aw，得，‎ 所以2（t+4）w﹣v（t+3）v﹣u=（t+4）w﹣u+（t+3）w﹣u，…‎ 当t为偶数时，2（t+4）w﹣v（t+3）v﹣u是偶数，而（t+4）w﹣u是偶数，（t+3）w﹣u是奇数，‎ 故2（t+4）w﹣v（t+3）v﹣u=（t+4）w﹣u+（t+3）w﹣u不能成立； …‎ 当t为奇数时，2（t+4）w﹣v（t+3）v﹣u是偶数，而（t+4）w﹣u是奇数，（t+3）w﹣u是偶数，‎ 故2（t+4）w﹣v（t+3）v﹣u=（t+4）w﹣u+（t+3）w﹣u也不能成立．…‎ 所以，对任意t∈N*，2（t+4）w﹣v（t+3）v﹣u=（t+4）w﹣u+（t+3）w﹣u不能成立，‎ 即数列{an}的任意三项都不成构成等差数列． …‎